1. PODSTAWOWE POJĘCIA I DEFINICJE

1.1. Pojęcie płynu

W zależności od warunków termodynamicznych, takich jak ciśnienie i temperatura, wszystkie ciała materialne występują w przyrodzie w trzech stanach skupienia: stałym, ciekłym i gazowym.

Stan skupienia każdego ciała determinowany jest stopniem ruchliwości jego atomów lub cząsteczek.

a) b) c)

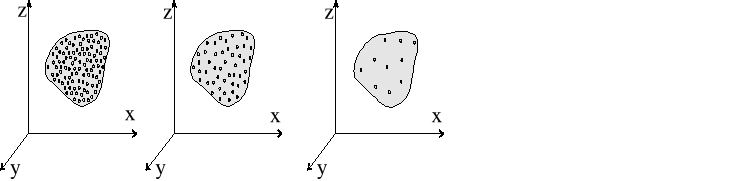
Rys.1.1. Poglądowa ilustracja stanu skupienia: a) ciała stałego, b) cieczy, c) gazu

Płynem nazywamy ciało materialne charakteryzujące się wielką ruchliwością cząsteczek, dzięki której podlega łatwo odkształceniom postaciowym pod wpływem działania nawet znikomo małych sił zewnętrznych oraz przyjmuje kształt naczynia, w którym się znajduje.

Płyny dzielimy umownie na: ciecze i gazy.

1. Charakterystyczne cechy cieczy:

a) posiadają samoistną objętość nie zachowując kształtu naczynia , w którym się znajdują,

b) odznaczają się bardzo małą ściśliwością, tzn. stawiają bardzo duży opór odkształceniom objętościowym; w praktyce ciecze uważać można jako płyny nieściśliwe, co jest równoznaczne z założeniem, że gęstość określonej cieczy ρ=const,

c) pozostając w stanie równowagi tworzą tzw. powierzchnię swobodną (zwierciadło)

2. Charakterystyczne cechy gazów:

a) nie wykazują samoistnej objętości, lecz wypełniają całkowicie każde naczynie, do którego są wprowadzone,

b) są bardzo ściśliwe, czyli wykazują znaczną podatność na odkształcenia objętościowe przy nawet znikomo małej zmianie ciśnienia,

c) nie tworzą powierzchni swobodnej,

d) wykazują sprężystość objętościową.

Przedstawiony powyżej podział płynów jest idealistyczny. W rzeczywistości występują znacznie bardziej złożone układy wielofazowe, tzn. mieszaniny rozdrobnionych ciał stałych, cieczy i gazów (zawiesiny, szlamy, roztwory niejednorodne, emulsje, układy fluidalne, pyły itp.).

1.2. Założenie ciągłości płynu

W klasycznej mechanice płynów płyn traktować będziemy jako ośrodek ciągły (continuum materialne). Pod pojęciem tym rozumieć będziemy bryłę geometryczną zawierającą nieskończoną ilość cząsteczek tworzących jednolitą strukturę materialną. Umożliwia to wyodrębnienie w takim ośrodku ciągłym, w otoczeniu dowolnego punktu A(x,y,z), nieskończenie małych elementów płynu, a przez przejście z ich wymiarami do granicy równej zero (x→0, y→0, z→0) - stosowanie aparatu analizy matematycznej. Z makroskopowego punktu widzenia elementy płynu muszą zawierać dostatecznie dużą ilość cząsteczek, aby prędkość, gęstość i inne parametry opisujące stan płynu w punkcie A(x,y,z) były wartościami średnimi dla zbioru cząsteczek wchodzących w skład elementu (rys.1.2)

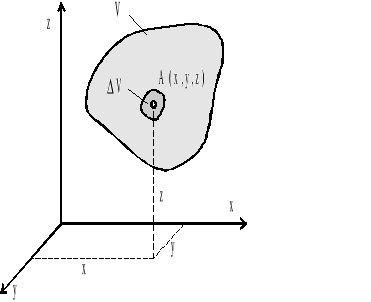
Rys.1.2. Element płynu rzeczywistego traktowanego jako ośrodek ciągły

Elementem płynu rzeczywistego nazywać będziemy taką jego objętość V, której wymiary liniowe są wielkościami małymi wyższego rzędu w porównaniu z wymiarami naczynia zawierającego płyn (lub ciała stałego zanurzonego w płynie), ale która - z drugiej strony - zawiera tak dużą liczbę cząsteczek płynu, że własności makroskopowe płynu, określone w odniesieniu do tej objętości, zachowują sens fizykalny.

W płynie rzeczywistym przejście graniczne V→0 nie ma sensu. Ma ono natomiast sens w przypadku wprowadzenia uproszczonego modelu płynu jako continuum materialne. Dzięki takiemu założeniu można określić makroskopowe własności płynu (np. ρ, p, T itp.) jako funkcje położenia i czasu oraz traktować je jako pola: skalarne, wektorowe lub tensorowe. Nie w każdym jednak przypadku założenie ciągłości płynu jest dopuszczalne. Dotyczy to zwłaszcza gazów rozrzedzonych określonych liczbą Knudsena

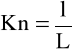
>0,01 (1.1)

gdzie:

l - średnia droga swobodną cząsteczek gazu,

L - charakterystyczny wymiar liniowy naczynia.

1.3. Rodzaje pól wielkości fizycznych

Załóżmy, że H jest dowolną wielkością fizyczną natomiast V - wydzielonym obszarem trójwymiarowej przestrzeni euklidesowej. Jeżeli każdemu punktowi A(x,y,z,t)∈V odpowiada dokładnie jedna wartość wielkości H wówczas mówimy, że w obszarze V określone zostało pole wielkości H. W zależności od tego, czy H jest wielkością skalarną, wektorową lub tensorową, pole H nazywamy odpowiednio: skalarnym, wektorowym lub tensorowym.

Pole wielkości fizycznej H jest:

1) jednorodne (homogeniczne) jeżeli

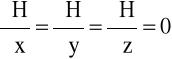
⇒ H=const (1.2)

2) niejednorodne - gdy

∨
∨
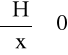
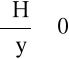
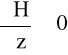
(1.3)

3) ustalone (stacjonarne), jeżeli

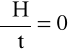
⇒ H=H(x,y,z) (1.4)

4) nieustalone (niestacjonarne) wówczas, gdy

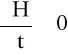
(1.5)

Ponadto pole wielkości H może być:

a) trójwymiarowe - H= H(x,y,z),

b) dwuwymiarowe - H= H(x,y), (np. pole płaskie, osiowo-symetryczne),

c) jednowymiarowe - H=H(x), gdzie x jest - na ogół - zmienną krzywoliniową.

1.4. Makroskopowe własności płynów

1.4.1. Gęstość i ciężar właściwy

Załóżmy, że dowolny obszar o objętości V wypełniony jest w sposób ciągły płynem (rys.1.3).

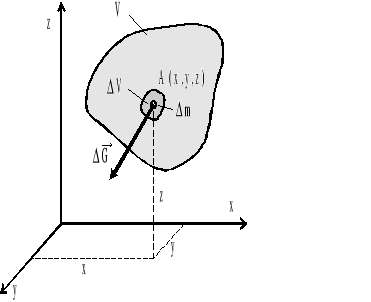
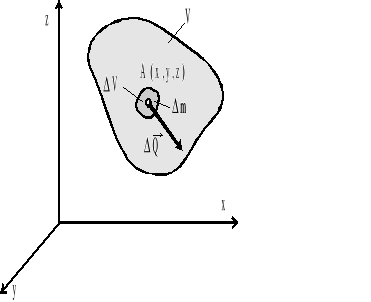
Rys.1.3. Obszar płynu o dowolnej objętości V i masie m oraz element płynu w otoczeniu punktu A(x,y,z) o objętości ΔV i Δm.

Wyodrębnijmy w otoczeniu punktu A(x,y,z) element płynu o objętości ΔV i masie Δm. Ciężar tego elementu, w jednorodnym polu sił ciężkości, wynosi ΔG.

Gęstością (masą właściwą) płynu w punkcie A(x,y,z) w chwili t nazywamy granicę ilorazu różnicowego (1.6).

(

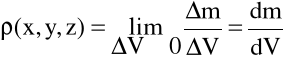
Ciężarem właściwym płynu w punkcie A(x,y,z) w chwili t nazywamy granicę ilorazu różnicowego (1.7).

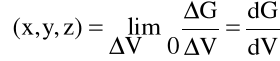
(1.7)

Ponieważ dG=g dm, zatem

(1.8)

W przypadku, gdy płyn jest jednorodny, wtedy

(

(

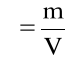
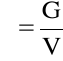
 Ściśliwość i rozszerzalność cieplna płynów

Ściśliwością płynu nazywamy jego zdolność do zmniejszania pierwotnej objętości wskutek działania sił zewnętrznych (ciśnienia).

Ściśliwość płynu określają:

a) współczynnik ściśliwości (iloraz względnej zmiany objętości do zmiany ciśnienia)

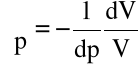
(1.11)

b) moduł sprężystości (odkształcenia objętościowego)

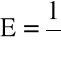
(1.12)

W przypadku płynu nieściśliwego (cieczy) β=0.

Rozszerzalność cieplna płynu charakteryzuje zmianę jego objętości pod wpływem dodatniego lub ujemnego przyrostu temperatury.

Jej miarą jest współczynnik rozszerzalności cieplnej, wyrażający względną zmianę objętości płynu przy zmianie temperatury o 1⁰ K

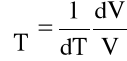
(1.13)

1.4.3 Lepkość płynu

Jedną z podstawowych własności poruszającego się płynu jest pewien opór stawiany siłom zewnętrznym podczas ścinania sąsiadujących ze sobą warstewek płynu. Siły te wywołują w płynie naprężenia styczne , które stanowią istotę tzw. lepkości lub tarcia wewnętrznego.

Lepkością nazywamy zdolność płynu rzeczywistego do przenoszenia naprężeń stycznych podczas jego ścinania.

W przeciwieństwie do zachowania się ciał stałych poddanych ścinaniu, płyny podlegają odkształceniu lepkościowemu, tzn. pod wpływem stałego naprężenia stycznego następuje przyrost odkształcenia postaciowego w czasie ścinania. Zjawisko takie nazywa się płynięciem. Lepkość, jako miara oporu stawianego przez płyn siłom ścinającym uwarunkowana jest jego strukturą cząsteczkową. Przy założeniu jednak, że płyn traktowany jest jako ośrodek ciągły, należy sformułować dodatkowe prawo fizyczne określające zależność między naprężeniem stycznym i prędkością wywołanego przezeń odkształcenia postaciowego.

Wyobraźmy sobie wyodrębnioną z całej objętości warstewkę płynu ograniczoną dwiema równoległymi płaszczyznami o polach dS i oddalonych od siebie o dy. Sytuację taką przedstawiono na rys.1.4. Załóżmy, że w ścinającym ruchu względnym dolna płaszczyzna jest nieruchoma, zaś górna przesuwa się równolegle do osi x pod wpływem przyłożonej do niej siły dP. Pierwotny element płynu w kształcie prostopadłościanu ulegnie, po czasie dt, odkształceniu postaciowemu przyjmując kształt równoległościanu. Zakładając, że kąt odkształcenia postaciowego γ jest mały, możemy napisać:

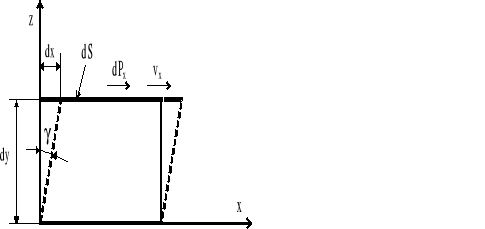
Rys.1.4. Interpretacją szybkości ścinania (prędkości odkształcenia postaciowego) w przypadku płaskiego przepływu Poiseuille'a.

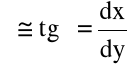
(1.14)

Obliczmy prędkość narastania odkształcenia postaciowego w czasie t, którą dalej nazywać będziemy szybkością ścinania

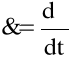
(1.15)

Uwzględniając w równaniu (1.15) zależność (1.14) , tzn.

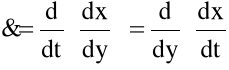
i zauważając, że

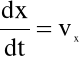
mamy

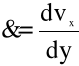
(1.16)

Zgodnie z hipotezą Newtona (zwaną również prawem tarcia wewnętrznego Newtona):

Naprężenie styczne w płynie jest wprost proporcjonalne do szybkości ścinania.

(1.17)

Współczynnik proporcjonalności w prawie Newtona  nosi nazwę dynamicznego współczynnika lepkości i zależy od rodzaju płynu, temperatury oraz ciśnienia.

Inną miarą lepkości płynu jest kinematyczny współczynnik lepkości  zdefiniowany jako stosunek dynamicznego współczynnika lepkości do gęstości płynu

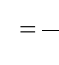
(1.18)

Wszystkie płyny spełniające prawo (1.17) nazywamy płynami newtonowskimi.

Zaliczyć do nich można wszystkie gazy oraz ciecze, które z reguły mają małą masę cząsteczkową. Pozostałe płyny, w tym niektóre układy wielofazowe, nie spełniają hipotezy Newtona (1.17) i wykazują znacznie bardziej złożone własności reologiczne. Noszą one nazwę płynów nienewtonowskich. Przykładem takich płynów są: roztwory polimerowe i koloidalne, zawiesiny, emulsje, pasty itp.

Do pomiaru dynamicznego lub kinematycznego współczynnika lepkości płynów newtonowskich stosuje się wiskozymetry. Zasady oznaczania lepkości za pomocą tych aparatów oraz podstawy ich konstrukcji opisano w p. 9.2.3.

1.5. Wyidealizowane modele płynu

Trudności matematyczne powstające przy rozwiązywaniu zagadnień przepływowych płynów rzeczywistych, z uwzględnieniem ich lepkości i ściśliwości, komplikują bardzo poważnie analityczny opis ich ruchu. W wielu problemach, zwłaszcza statyki i kinematyki płynów, można znacznie uprościć rozważania teoretyczne wprowadzając model płynu doskonałego. Przydatny jest on również przy formułowaniu podstawowych równań i wzorów dynamiki płynów, które - po wprowadzeniu odpowiednich współczynników poprawkowych - przydatne są do obliczania układów hydraulicznych.

Płynem doskonałym nazywamy fikcyjny płyn odznaczający się zupełnym brakiem lepkości. Nie przenosi on zatem naprężeń stycznych, a występujące w nim naprężenia normalne mogą być wyłącznie ciśnieniami.

Szczególnymi przypadkami płynu doskonałego są:

a) ciecz doskonała, tzn. nieściśliwy płyn nie lepki, który nie paruje, nie zamarza i nie pochłania gazów,

b) gaz doskonały, tzn. ściśliwy płyn doskonały spełniający równanie stanu Clapeyrona

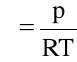
(1.19)

Powierzchnia kontrolna i powierzchnia płynna

a) b)

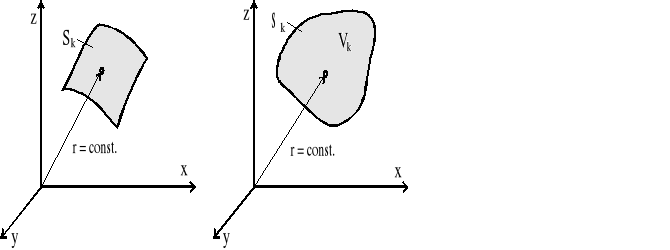
Rys.1.5. a) - otwarta powierzchnia kontrolna,

b) - obszar kontrolny ograniczony zamkniętą powierzchnią kontrolną

Powierzchnią kontrolną (rys.1.5a) nazywamy dowolną (otwartą lub zamkniętą) powierzchnię w obszarze wypełnionym poruszającym się płynem, odznaczającą się tym, że położenie każdego jej punktu nie ulega zmianie względem przyjętego układu odniesienia z upływem czasu. Powierzchnię kontrolną tworzą, zatem stale te same punkty w przestrzeni, natomiast znajdują się na niej - w miarę upływu czasu - coraz to inne elementy płynu (traktowane jako punkty materialne).

Objętość ograniczona zamkniętą powierzchnią kontrolną (rys.1.5b) nosi nazwę obszaru kontrolnego.

Powierzchnią płynną nazywać będziemy dowolną powierzchnię w polu prędkości płynu charakteryzującą się tym, że tworzą ją stale te same punkty materialne płynu w chwili czasu t, natomiast jej kształt i położenie względem przyjętego układu odniesienia mogą ulegać zmianom z upływem czasu.

Obszar płynu ograniczony zamkniętą powierzchnią płynu nazywany jest obszarem płynnym (rys.1.6).

a) b)

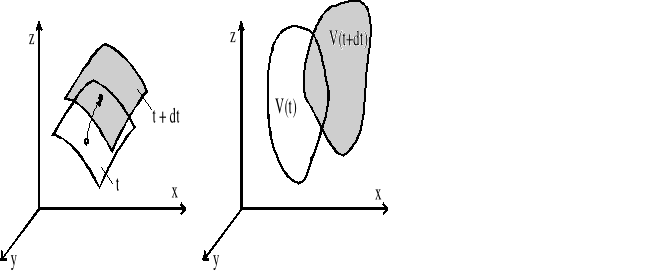
Rys.1.6. a) otwarta powierzchnia płynna w danej chwili czasu t i w chwili t+dt

b) zamknięta powierzchnia płynna ograniczająca obszar płynny w chwilach t i t+dt

1.7. Siły działające na płyn

Siły działające na wyodrębniony element płynu można ogólnie podzielić na:

1) siły masowe (objętościowe)

2) siły powierzchniowe

Siły masowe związane są z masą płynu. Są one wynikiem oddziaływania określonego, zewnętrznego pola przyśpieszeń na każdy element płynu, np. siła ciężkości, bezwładności itp. Wartość liczbowa siły masowej
punkcie A(x,y,z) jest zawsze proporcjonalna do masy elementu płynu m zawartej w otoczeniu punktu A (rys.1.7) Współczynnikiem proporcjonalności w tej zależności jest tzw. jednostkowa siła masowa
zdefiniowana za pomocą wzoru

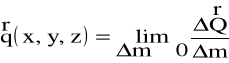
(1.20)

przy czym

(1.21)

gdzie X, Y, Z są składowymi jednostkowej siły masowej
.

Rys.1.7. Siła masowa w wybranym punkcie płynu traktowanego jako ośrodek ciągły

Siły powierzchniowe dzielimy na:

a) zewnętrzne - występujące między ściankami naczynia a wypełniającym je płynem (napór hydrostatyczny) lub między ciałem stałym i opływającym je płynem,

b) wewnętrzne - działające na wyodrębnione myślowo elementy płynu lub powierzchnie płynne.

Siły powierzchniowe rozłożone są zawsze w sposób ciągły na powierzchni i opisywane są za pomocą naprężeń.

Zakładać będziemy, że płyn nie przenosi naprężeń rozciągających, tzn. składowe normalne naprężeń mogą być tylko ciśnieniami.

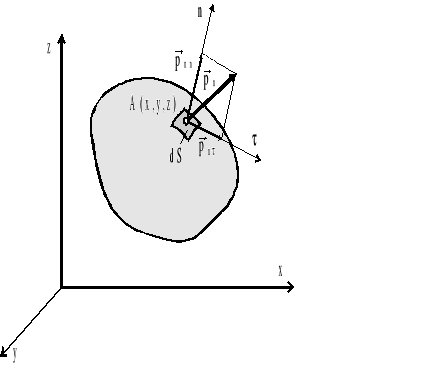
Rys.1.8. Naprężenie
w punkcie A(x,y,z) płynu.

Naprężeniem
w punkcie A(x,y,z) płynu (rys.1.8) nazywamy granicę ilorazu różnicowego

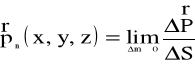
(1.22)

W zależności od orientacji elementu powierzchniowego poprowadzonego przez dany punkt, naprężenie
można przedstawić, na niezliczoną ilość sposobów, w postaci sumy geometrycznej naprężenia normalnego
i stycznego
tj.

(1.23)

Uwaga! Pierwszy dolny indeks w równaniu (1.23) oznacza kierunek normalnej do elementu powierzchniowego na który działa naprężenie natomiast drugi dolny indeks oznacza kierunek prostej na którą zrzutowane zostało naprężenie
.

Podstawowa różnica między wektorami
i
polega na tym, że o ile jednostkowa siła masowa jest funkcją położenia i czasu to naprężenie jest funkcją - obok czasu i położenia - także orientacji elementu powierzchniowego

(1.24)

gdzie

n_x=cos(x,n)

n_y=cos(y,n) (1.25)

n_z=cos(z,n)

W przypadku ruchu lub równowagi płynu doskonałego oraz cieczy lepkiej znajdującej się w stanie spoczynku składowa styczna naprężenia p_n znika; pozostaje jedynie składowa normalna, która co do wartości bezwzględnej równa się ciśnieniu hydrostatycznemu p.

(1.26)

W rozdziale 2., p. 2.1 wykażemy że ciśnienie hydrostatyczne w punkcie A nie zależy od orientacji elementu powierzchniowego poprowadzonego przez ten punkt, a zatem może być uważane za wielkość skalarną.

---