STATYKA PŁYNÓW
Statyka płynów to dział mechaniki płynów obejmujący prawa równowagi płynów
znajdujących się w spoczynku oraz zagadnienia praktycznego zastosowania tych praw. Równowaga
płynu może mieć charakter bezwzględny i względny. W obu przypadkach poszczególne elementy
płynu nie zmieniają swego położenia względem siebie i względem otaczających ścian. W przypadku
równowagi bezwzględnej nie zmieniają również swego położenia względem Ziemi.
1.WARUNKI RÓWNOWAGI PŁYNÓW. PRAWO PASCALA
Równanie równowagi płynu otrzymuje się bezpośrednio z równań ruchu (3.33) lub (3.34) po
uwzględnieniu, że w rozpatrywanych zagadnieniach prędkość jest równa zeru (v = 0), a pozostałe
wielkości nie zależą od czasu (∂ H/∂ t = 0).
Równanie równowagi płynu przyjmuje, zatem postać
ρf = gradρ
(1.1)
Lub w formie trzech równań
𝑝𝑋 =
𝜕𝑝
𝜕𝑥
,
𝑝𝑌 =
𝜕𝑝
𝜕𝑦
,
𝑝𝑍 =
𝜕𝑝
𝜕𝑧
(1.2)
Równanie to jest podstawowym równaniem równowagi płynów i nosi nazwę równania
równowagi Eulera.
Mnożąc poszczególne równania układu kolejno przez dx, dy, dz i dodając stronami,
otrzymamy
ρ( Xdx – Ydy – Zdz ) =
𝜕𝑝
𝜕𝑥
𝑑𝑥 −
𝜕𝑝
𝜕𝑦
𝑑𝑦 −
𝜕𝑝
𝜕
𝑑𝑧
(1.3)
Ponieważ ciśnienie nie zależy od czasu, prawa strona tego równania jest, zatem różniczką
zupełną funkcji p = p (x, y, z):
dp =
𝜕𝑝
𝜕𝑥
𝑑𝑥 +
𝜕𝑝
𝜕𝑦
𝑑𝑦 +
𝜕𝑝
𝜕𝑧
𝑑𝑧
Czyli,
dp = ρ(Xdx +Ydy + Zdz) (1.4)
Jest to tak zwane podstawowe równanie hydrostatyki, określające zależność między
ciśnieniem i jednostkowymi siłami masowymi działającymi na płyn znajdujący się w spoczynku.
Gdy na płyn nie działają siły masowe, z równania równowagi (1.2) wynika, że
f = 0
⇒ grad p = 0 ⇒ p = const, (1.5)
Gdyby na płyn działały tylko siły powierzchniowe, ciśnienie miałoby wówczas jednakową
wartość w każdym punkcie płynu. Stanowi to treść prawa Pascala - Prawo równomiernego
rozchodzenia się ciśnienia w płynie”.
Brak sił masowych oznacza, że płyn jest nieważki. Ten warunek w polu sił ciężkości
spełniają w przybliżeniu gazy i wszystkie płyny w stanie nieważkości. Prawo Pascala stosuje się
również w przybliżeniu do płynów znajdujących się pod działaniem pola sił masowych, jeżeli są one
pomijalnie małe w porównaniu z siłami pochodzącymi od ciśnień. Warunki te zachodzą w
urządzeniach zawierających płyny pod dużymi ciśnieniami (sprężarki tłokowe, akumulatory wodne,
prasy hydrauliczne, itp.).
Podczas rozwiązywania podstawowego równania hydrostatyki (1.4). Oprócz określonych
warunków brzegowych, należy wziąć pod uwagę równanie stanu płynu. Opisujące zmiany gęstości
w zależności od ciśnienia i temperatury.
p = p(p, T)
(1.6)
Określenie związku między ciśnieniem i jednostkowymi siłami masowymi jest jednym z dwu
charakterystycznych zagadnień statyki płynów. Drugim jest znalezienie równania powierzchni
izobarycznej
p = const
⇒ dp = 0
Równanie różniczkowe powierzchni izobarycznej ma, więc postać
X dx + Y dy + Z dz = 0
(1.7)
Lewa strona tego równania jest iloczynem skalarnym wektorów, f ≡ (X, Y, Z) i dr ≡ (dx, dy,
dz), wobec tego wynika z niego, że wektor siły masowej, w każdym punkcie obszaru płynnego, jest
prostopadły do powierzchni izobarycznej przechodzącej przez ten punkt. Powierzchnie izobaryczne
w jednorodnym polu sił masowych są, więc płaszczyznami.
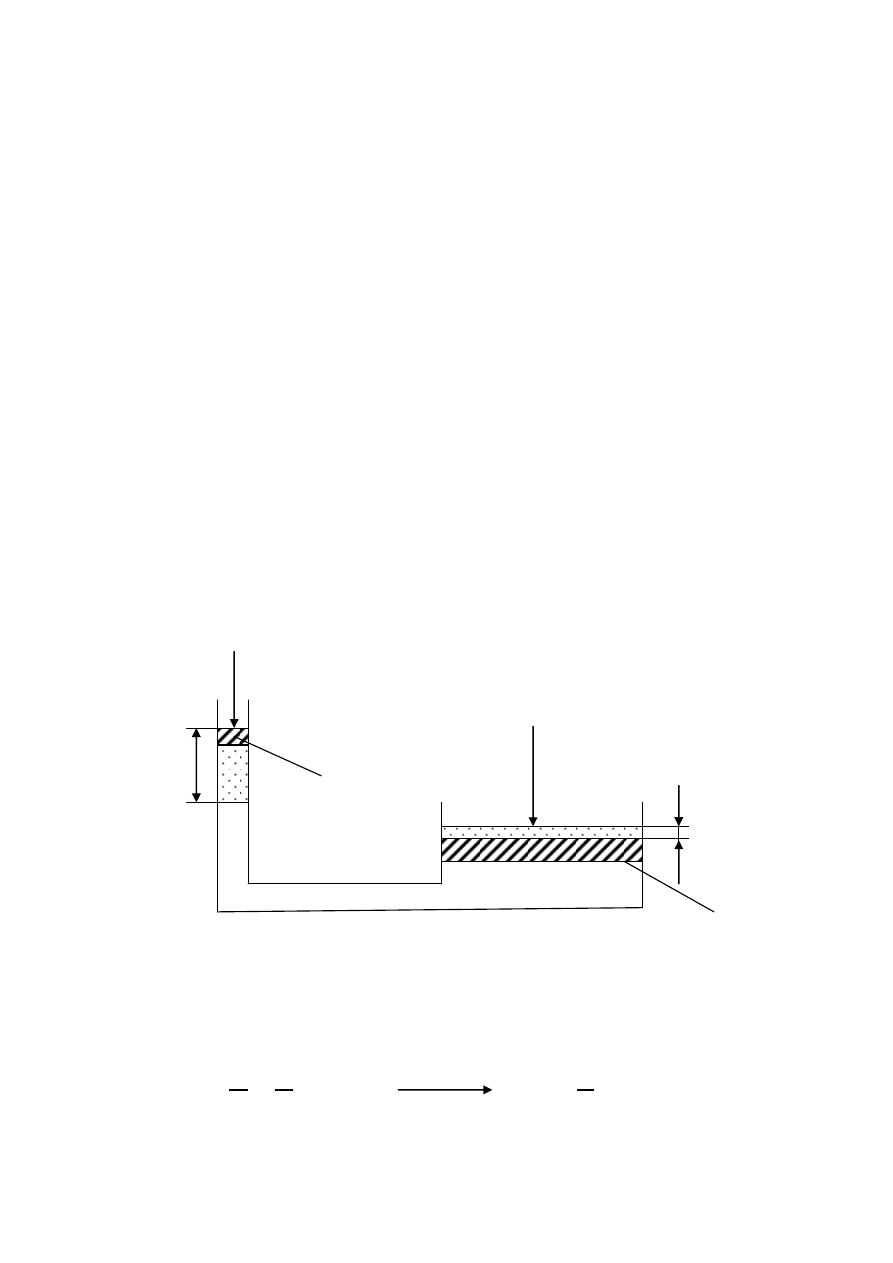
PRZYKŁAD 1
P1
P2
h
1
S1
h
2
S2
SCHEMAT PRASY HYDRAULICZNEJ
Zgodnie z prawem Pascala ciśnienie w każdym punkcie cieczy „roboczej” jest stałe i równe
p
=
𝑃1
𝑆1
=
𝑃2
𝑆2
,
(1.a)
P2= P1
𝑆2
𝑆1
,
(1.b)
W przypadku tłoków cylindrycznych o średnicach
d i D: S1 =
𝜋
𝑑
2
4
, S2 =
𝜋
𝐷
2
4
, a
zależność (1.a) ma postać
P2 =
𝐷
𝑑
2
P1
(1.c)
Na przykład niech
𝐷
𝑑
= 10 to P2 = 100P1. Praca włożona przy przesunięciu jednego tłoka o h1,
drugiego o h2, pomijając ściśliwych cieczy: i spełnia równanie ciągłości
S1h1
= S2h2
Stąd wobec
(1.c)
mamy
L
1
=P1h1=P1
𝑆2ℎ2
𝑆1
=P1
𝑃2
𝑃1
ℎ1=P2h2=L
2
Czyli praca włożona jest równa pracy otrzymanej.
2.SIŁA WYPORU. PRAWO ARCHIMEDESA
Kiedy ciało jest zanurzone w całości lub częściowo w spoczywającym płynie (cieczy lub
gazie) to płyn ten wywiera ciśnienie na każdą część powierzchni ciała. Wypadkowa siła jest
skierowana ku górze i nazywa Się siłą wyporu.
P
c
Δh
P + ΔP
POWSTAWANIE SIŁY WYPORU DZIAŁAJACEJ NA CIAŁO ZANURZONE W CIECZY
Wyliczmy siłę wyporu dla ciała w kształcie prostopadłościanu o polu powierzchni podstawy
S oraz wysokości, Δh. Łatwo zauważyć, że siły działające na ścianki boczne równoważą się. Siła
wypadkowa
𝜚
S
Q=S(p+Δp) – Sp = SΔp.
Lecz
Δp=
𝜚
c
gΔh
(gdzie
c
jest gęstością cieczy),
A zatem:
Q=SΔh
𝜚
c
g=V
𝜚
c
g.
Tak, więc:
Q = V
𝜚
c
g
Otrzymaliśmy prawo Archimedesa:
Ciało zanurzone w płynie jest wypierane ku górze siłą równą ciężarowi wypartego przez to
ciało płynu.
Prawo to jest słuszne dla ciała o dowolnym kształcie, a nie tylko dla rozważanego przypadku
sześcianu. Zauważmy, że warunkiem pływania ciała jest, aby ciężar ciała (P) był mniejszy od siły
wyporu (Q): P
≤ 𝑄. , 𝑃𝑜𝑛𝑖𝑒𝑤𝑎ż P=V
g (gdzie
jest gęstością ciała), więc warunek pływania ciała:
ρ
c
≤
ρ
c
3.CIŚNIENIE I GĘSTOŚĆ CIECZY
Różnica w działaniu siły na płyn, a ciało stałe polega na tym, że w spoczywającej cieczy siła
musi być zawsze prostopadła do powierzchni płynu, podczas gdy w ciele stałym może mieć dowolny
kierunek. Spoczywający płyn nie może równoważyć sił stycznych (warstwy płynu ślizgałyby się po
sobie) i dlatego może zmieniać kształt i płynąć. Wygodnie jest, więc opisywać siłę działającą na płyn
za pomocą ciśnienia p zdefiniowanego, jako wartość siły prostopadłej działającej na jednostkę
powierzchni. Ciśnienie jest przekazywane na sztywne ścianki naczynia, a także na dowolne przekroje
płynów prostopadle do tych ścianek i przekrojów w każdym punkcie. Ciśnienie jest wielkością
skalarną
W układzie SI jednostką jest Pascal: 1 Pa = 1 N/m
2
. Na uwagę zasługuje też jednostka bar (1
bar = 10
5
Pa), gdyż tyle wynosi w przybliżeniu ciśnienie atmosferyczne.
Płyn znajdujący się pod ciśnieniem wywiera siłę na każdą powierzchnię będącą z nim w
kontakcie. Rozważmy zamkniętą powierzchnię zawierającą płyn (rysunek). Dowolny element
powierzchni jest reprezentowany przez wektor S (długość tego wektora równa jest reprezentowanej
powierzchni, jego kierunek prostopadły do niej, zwrot na zewnątrz). Wtedy siła F wywierana przez
płyn na ten element powierzchni wynosi:
F = pS
(2.1)
Ponieważ F i S mają ten sam kierunek, więc ciśnienie p można zapisać
p =
𝐹
𝑆
(2.2)
Inną wielkością fizyczną charakteryzującą własności płynów jest ich gęstość
(𝜌). Dla płynów
jednorodnych gęstość zdefiniowana jest jako masa płynu podzielona przez objętość (jednostką jest kg/m
3
lub
g/cm
3
). Gęstość płynu może zależeć od szeregu czynników takich jak temperatura czy ciśnienie. Dla cieczy,
nawet przy stosunkowo dużych zmianach ciśnienia i temperatury, gęstość zmienia się nieznacznie, dlatego
określamy je mianem płynów nieściśliwych. Gęstość gazów, natomiast, jest bardzo czuła na zmiany ciśnienia
i temperatury
. Gęstość określa się wzorem:
𝜚
=
𝑚
𝑉
(5.1)
4.ROZKŁAD CIŚNIENIA
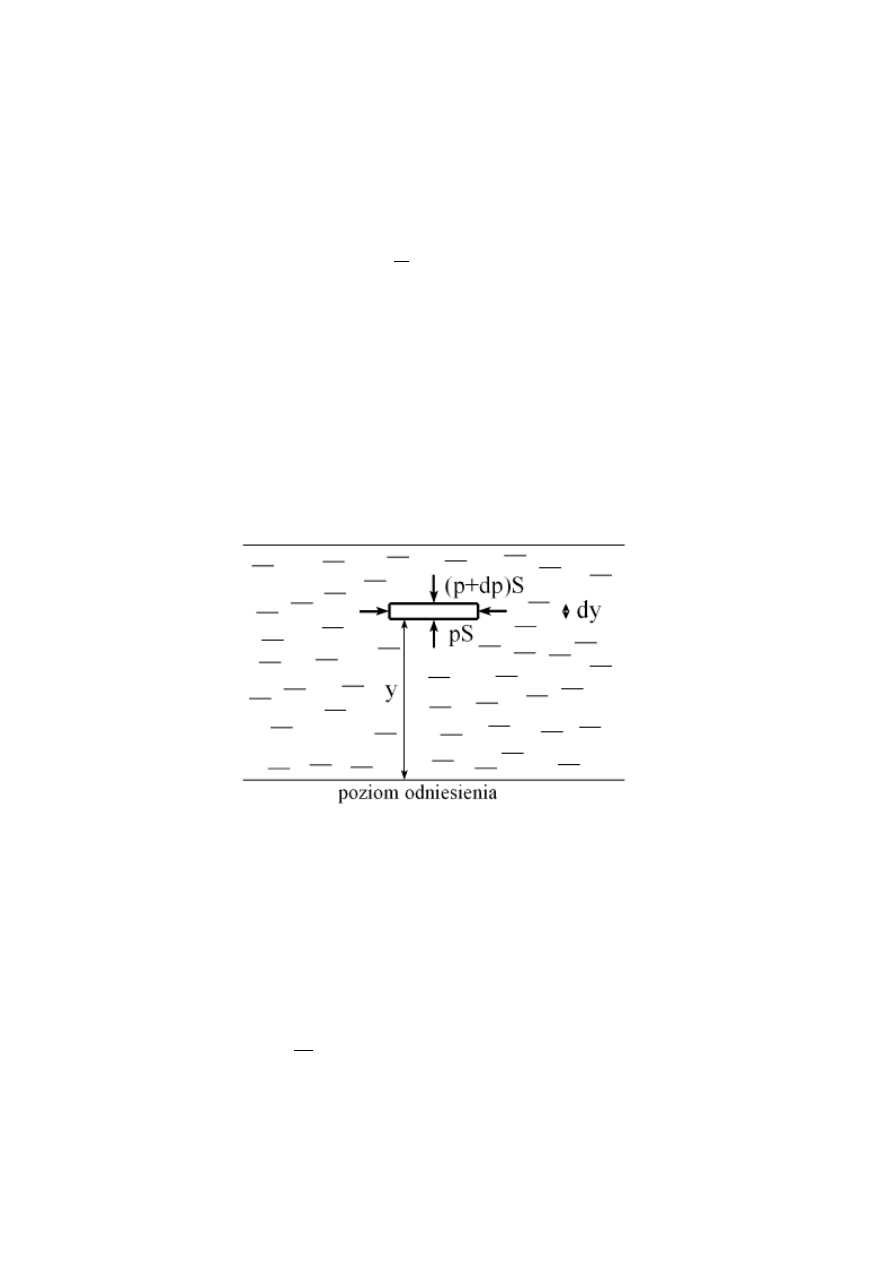
W płynie znajdującym się w równowadze każda jego część pozostaje w spoczynku.
Rozpatrzmy element cieczy w kształcie cienkiego dysku znajdującego się w odległości y od jakiegoś
poziomu
Odniesienia.
Grubość dysku wynosi dy, a jego pozioma powierzchnia wynosi S. Masa elementu wynosi
Sdy, a jego ciężar
gSdy. Siły poziome, wywołane jedynie przez ciśnienie płynu, równoważą się.
Siły pionowe są wywoływane nie tylko przez ciśnienie płynu, ale też przez jego ciężar. Element
płynu jest w spoczynku, a więc wypadkowa siła działająca nań musi być zerem. Dla zachowania
równowagi w pionie trzeba, więc by:
pS = (p+dp)S +
𝜚gSdy
(3.1)
Gdzie (p+dp) to ciśnienie na górną powierzchnię a p na dolną, a stąd
𝑑𝑝
𝑑𝑦
= −𝜚𝑔
(3.2)
Równanie to pokazuje, że ciśnienie maleje wraz z wysokością. Powodem jest ciężar warstwy
płynu leżącego pomiędzy punktami, dla których mierzymy różnice ciśnień. Jeżeli P
1
jest ciśnieniem
na wysokości Y
1
a P
2
ciśnieniem na wysokości Y
2
to całkując powyższe równanie mamy:
𝑑𝑝
𝑃
1
𝑃
2
= − 𝜚𝑔𝑑𝑦
𝑌
2
𝑌
1
(3.3)
Lub
𝑃
1
− 𝑃
2
= − 𝜚𝑔𝑑𝑦
𝑌
2
𝑌
1
(3.4)
Przyjmując ρ i g za stałe otrzymamy:
𝑃
2
− 𝑃
1
= −𝜚𝑔 𝑌
2
− 𝑌
1
(3.5)
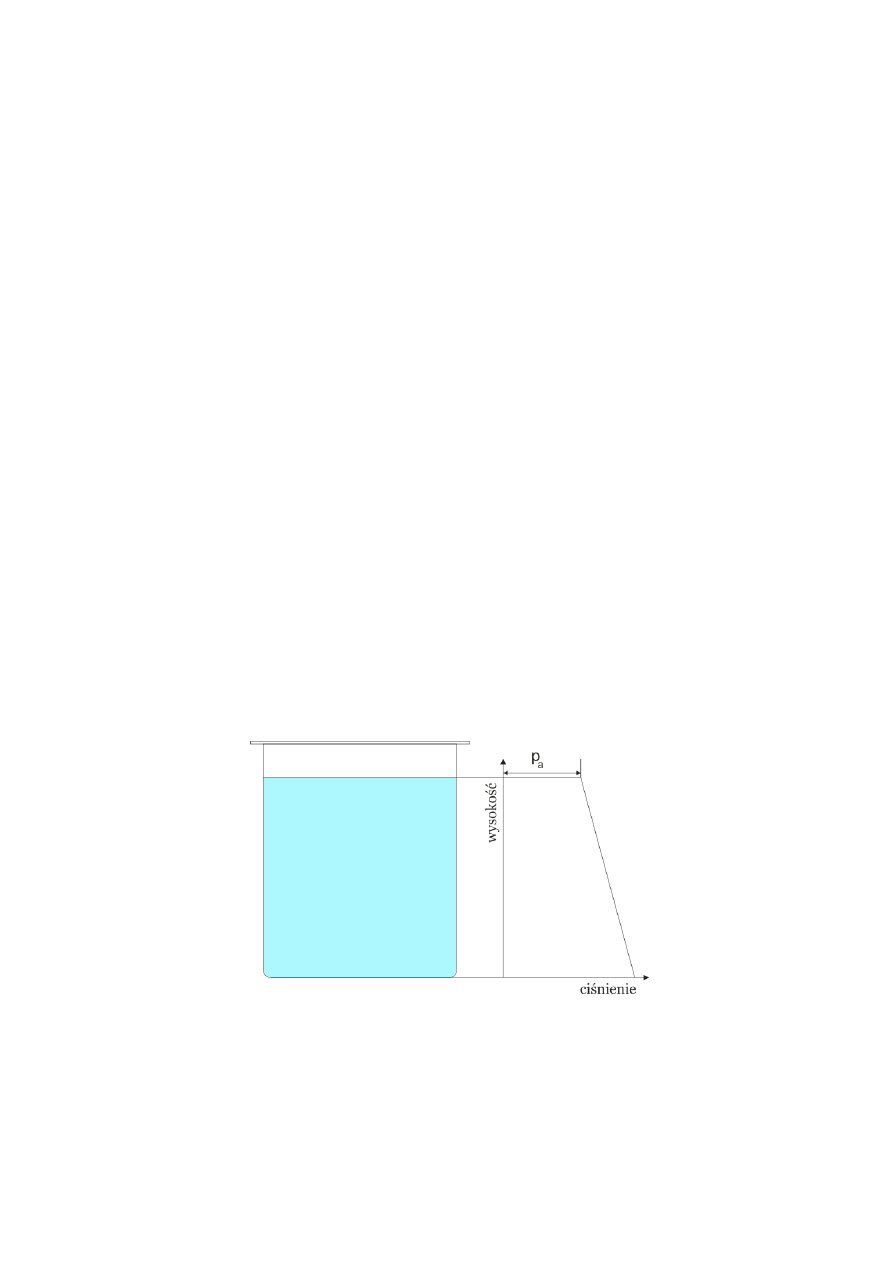
Wygodnie jest przyjąć powierzchnie cieczy, jako poziom odniesienia
𝑌 = 𝑌
2
Zauważmy
ponadto, iż ciśnienie
𝑃
2
(na powierzchni) jest równe ciśnieniu atmosferycznemu 𝑃
0
Różnica
ℎ = 𝑌
2
− 𝑌
1
opisuje położenie pewnego poziomu w cieczy względem powierzchni (licząc w głąb).
Ciśnienie na tej głębokości oznaczmy
𝑃 = 𝑃
2
Wtedy
𝑃
0
− 𝑃 = −𝜚𝑔ℎ
(3.6)
Lub
𝑃 = 𝑃
0
+ 𝜚𝑔ℎ
(3.7)
Związek ten pokazuje, że ciśnienie rośnie wraz z głębokością i że jest jednakowe dla
punktów o tej samej głębokości a zależność te pokazuje poniższy rysunek
ZMIANA CIŚNIENIA W CIECZY
Zastanówmy się teraz jak ciśnienie zmienia się wewnątrz gazu. Gęstość gazu
𝜚, jest
zazwyczaj mała w porównaniu z cieczą. Powoduje to, że różnica ciśnień między dwoma punktami
naczynia (o niezbyt dużych rozmiarach) wypełnionego gazem jest na ogół, do pominięcia i dlatego
można przyjmować, że ciśnienie gazu w naczyniu jest wszędzie jednakowe. Nie jest to jednak
prawdziwe, gdy mamy do czynienia ze znaczną różnicą wysokości (np., gdy wznosimy sie w
atmosferze). Ciśnienie zmienia się wtedy znacznie, (o czym przekonują się np. alpiniści), zmienia sie
też i gęstość
𝜚. Dlatego też, aby scałkować równanie
𝑑𝑝
𝑑𝑦
= −𝜚𝑔, musimy znać, 𝜚 jako funkcję y.
Z równania stanu gazu można łatwo wykazać, że
𝜌 jest proporcjonalne do ciśnienia (𝜚 ~ p)
przy, T=const. Opierając się na tej zależności, wyliczmy ciśnienie p powietrza na wysokości y ponad
poziomem morza. Użyjemy Równania (3.8)
𝑑𝑝
𝑑𝑦
= −𝜚𝑔
(3.8)
Ponieważ
𝜌~p, więc
𝜚
𝜚
0
=
𝑃
𝑃
0
(3.9)
Gdzie
𝜌
0
i
𝑃
0
to znane wartości gęstości i ciśnienia na poziomie morza. Wstawiając
𝜌 𝜌 =
𝑝𝜌
0
/𝑝
𝑜
z powyższego równania (3.8) Otrzymujemy:
𝑑𝑝
𝑑𝑦
= −𝑔𝜚
0
𝑃
𝑃
𝑜
(3.10)
Całkując to wyrażenie od p
o
w punkcie y=0 (poziom morza) do p w punkcie y nad poziomem
morza mamy:
𝑙𝑛
𝑝
𝑝
0
= −
𝑔𝜚
0
𝑝
0
𝑦
(3.11)
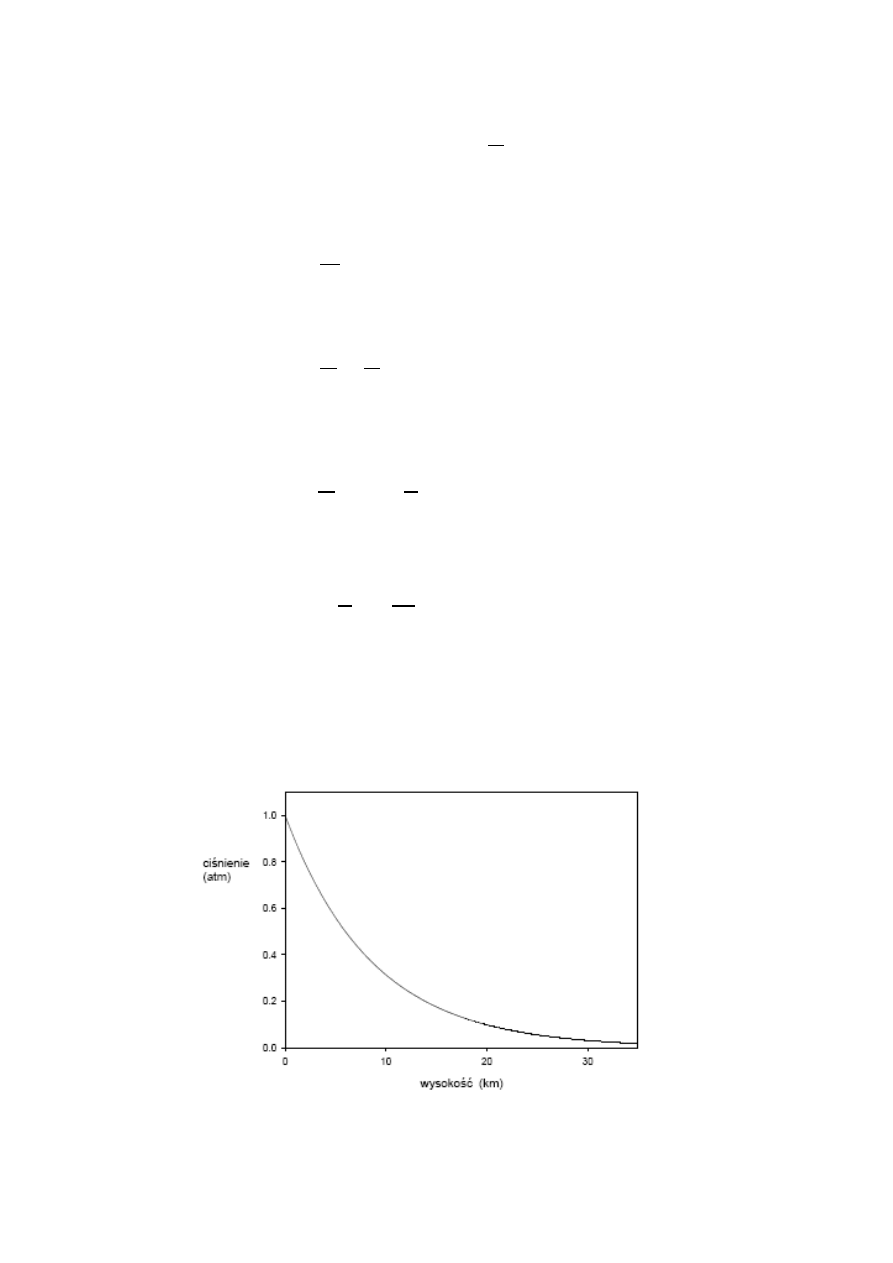
Zależność tę przestawia poniższy rysunek
ZMIAN CIŚNIENIA WRAZ Z WYSOKOŚCIĄ W POWIETRZU. WYSOKOŚĆ LICZONA OD
POZIOMU MORZA. KRZYWA WEDŁUG RÓWNANIA (3.11)
Rzeczywista zmiana ciśnienia z wysokością różni się trochę od tego, co przewiduje równanie
(3.11), (Temperatura powietrza maleje wraz z wysokością, co wpływa na zmianę gęstości, czego
tutaj nie uwzględniliśmy), niemniej powyższa zależność jest niezłym przybliżeniem
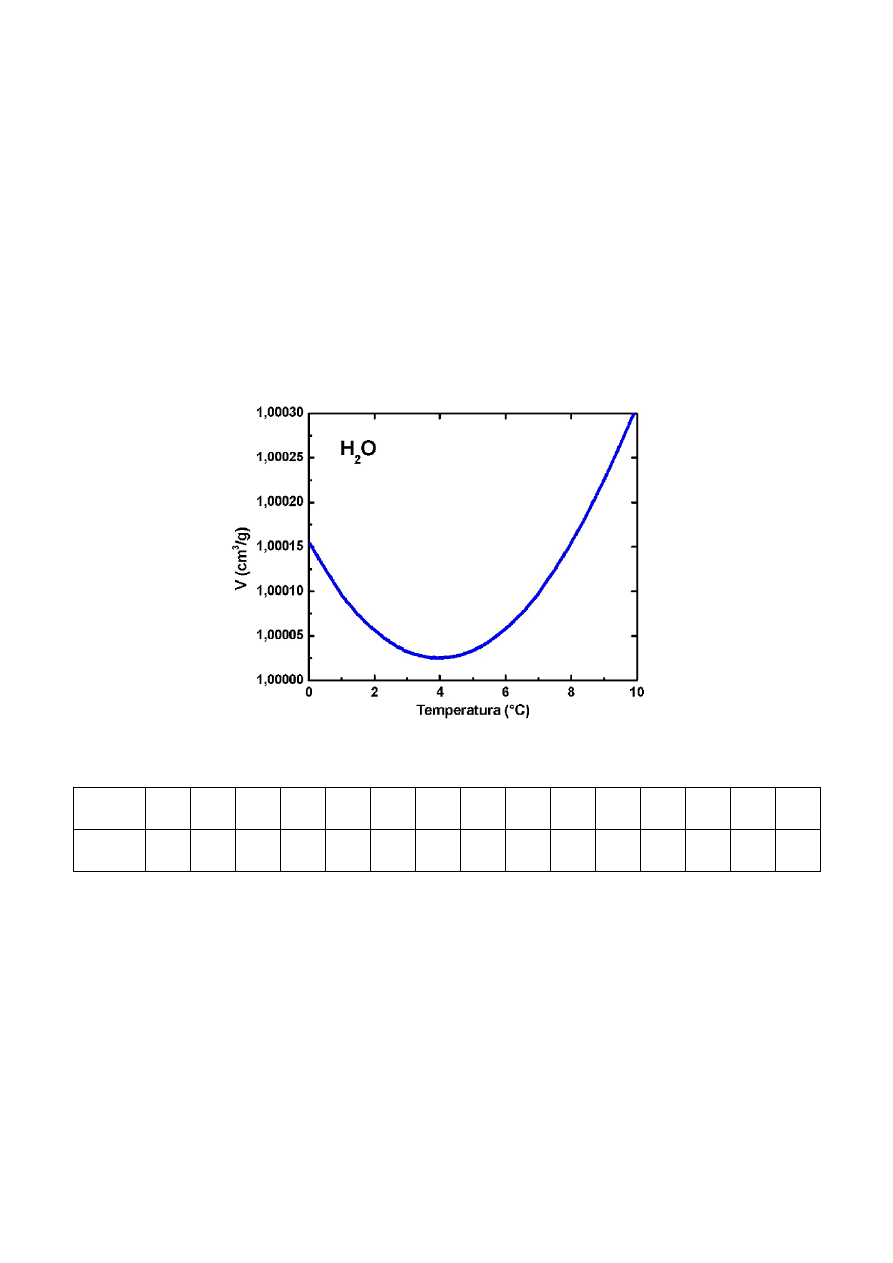
5. ZMIANA GĘSTOŚCI
Gęstość zależy od wielu czynników takich jak temperatura, ciśnienie.
Gęstość większości
substancji zmniejsza się wraz ze wzrostem temperatury (jednym z wyjątków jest woda w temperaturze
poniżej 4 °C). Zjawisko to wynika z rozszerzalności cieplnej ciał. Podczas przemian fazowych gęstość
zmienia się skokowo (w temperaturze przemiany), podczas krzepnięcia zazwyczaj wzrasta (najbardziej
znanymi wyjątkami są woda).
WYKRES ZMIANY GĘSTOŚCI CIECZY (WODY) W ZALEŻNOŚCI OD TEMPERATURY
Temp
[C
o
]
100
80
60
40
30
25
22
20
15
10
4
0
-10
-20
-30
Gęstość
[kg/m
3
]
958,
4
971,
8
983,
2
992,
2
995,
65
997,
04
997
,77
998,
20
999,
10
999,
70
999
,97
999,
83
998,
11
993,
54
983,
85
DANE TABELARYCZNE ZMIANY GĘSTOŚCI CIECZY (WODY) W ZALEŻNOŚCI OD
TEMPERATURY
6.ROZKŁAD TEMPERATURY W ATMOSFERZE ZIEMSKIEJ
Atmosferę charakteryzują czynniki zmieniające się z odległością od powierzchni ziemi, położeniem
geograficznym i czasem. Czynniki najważniejsze to:
temperatura, ciśnienie, gęstość
skład chemiczny
ładunek elektryczny
swobodne drgania cząsteczek gazów tworzących atmosferę
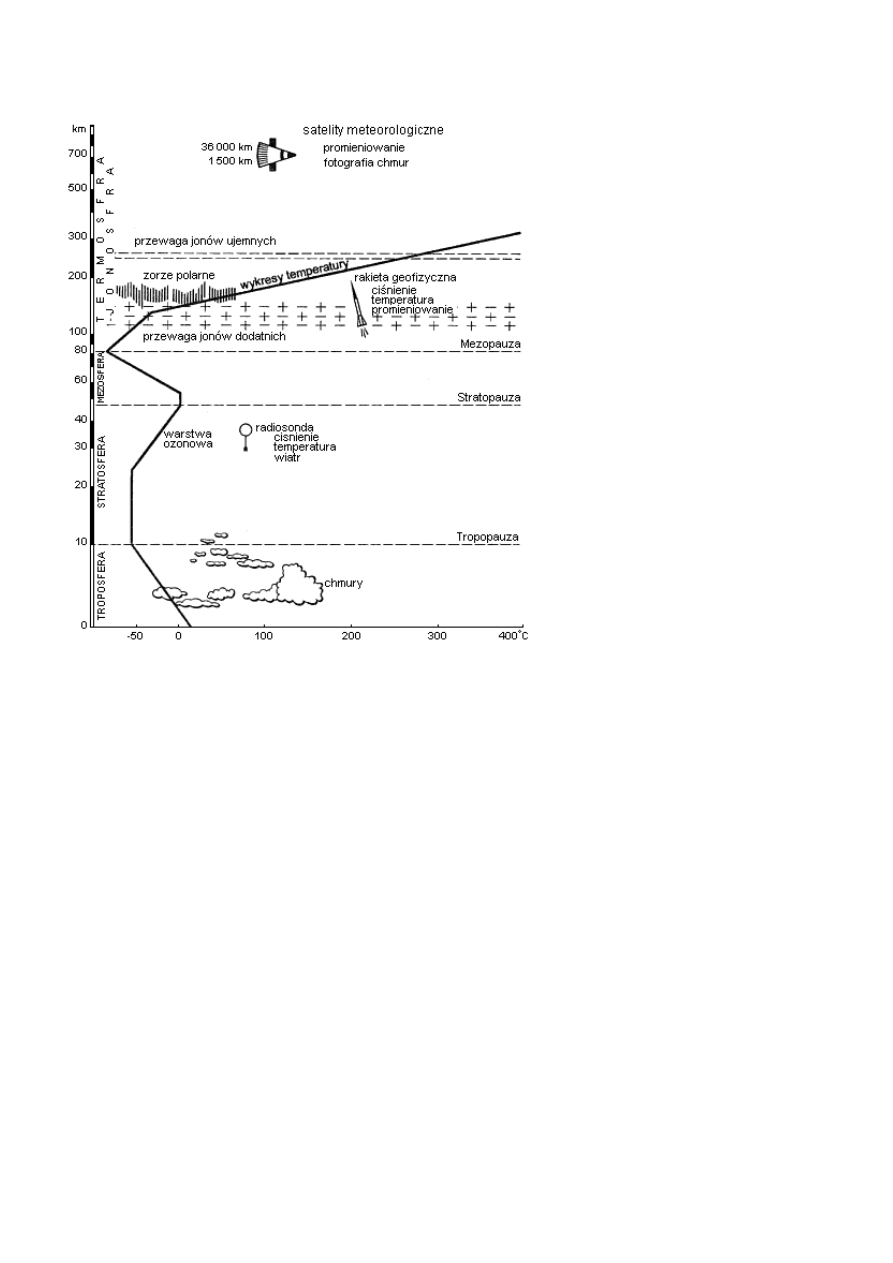
Tropsfera - Górna jej granica
zmienia się w zależności od pory
roku i od szerokości geograficznej.
Nad biegunami sięga ona do 7 km,
nad równikiem zasięg troposfery
waha się 18 km przez cały rok.
Charakterystyczną cechą tej warstwy
jest ciągły spadek temperatury wraz
ze wzrostem wysokości, przeciętnie
0,6 °C
na
100
m.
Ciśnienie
atmosferyczne
maleje
wraz
ze
wzrostem wysokości od około 1000
hPa na poziomie morza do około 200
hPa na granicy z tropopauzą. W
troposferze
zachodzą
częste
turbulencje
powietrza
oraz
najważniejsze procesy kształtujące
pogodę i klimat na Ziemi. Prowadzi
się w niej badania meteorologiczne i
klimatologiczne.
Stratosfera - od 15-20 km do ok. 45-
55 km. W dolnej części stratosfery
panuje prawie stała temperatura
powietrza, począwszy od wysokości
30-50 km temperatura rośnie wraz ze
wzrostem wysokości. Temperatura w
górnej części wzrasta do 15 stopni
Celsjusza. W niej znajduje się
warstwa ozonowa. Stratosfera skupia około 21% masy powietrza. Występują w niej chmury iryzujące
(perłowe).
Mezosfera - od 45-50 km do 80-85 km między stratosferą a mezopauzą, w której temperatura powietrza
maleje wraz ze wzrostem wysokości (od ok. 0 °C do ok. –70 °C). W pobliżu jej górnej granicy czasami w
nocy można zaobserwować, tzw. obłoki świecące, znane też, jako obłoki srebrzyste. Ciśnienie poniżej 1 hPa.
Termosfera - od ok. 85 km do ok. 500-600 km. Termosfera położona jest nad mezosferą. W termosferze
temperatura wzrasta wraz z wysokością do 1500-2000 K w górnej granicy wskutek pochłaniania
nadfioletowej części widma promieniowania słonecznego. Głównym składnikiem termosfery jest tlen
atomowy. W tej warstwie występują zorze polarne. W dolnej części termosfery - jonosferze - cząsteczki
gazów ulegają jonizacji, co wiąże się ze zjawiskiem odbijania oraz pochłania fal radiowych w tej warstwie.
Międzynarodowa Stacja Kosmiczna porusza się na stałej orbicie w górnej części termosfery, pomiędzy 320-
380 km.
7.ROZKŁAD CISNIENIA I GĘSTOŚCI W ATMOSFERZE ZIEMSKIEJ
Przyjmując, że osie X, Y układów współrzędnych wyznaczają powierzchnie Ziemi, a os Z jest
zwrócona ku górze składowe jednostki siły masowej są równe
𝑋 = 𝑌 = 0, 𝑍 = −𝑔
(7.1)
Równanie
𝑑𝑝 = −𝜚𝑔𝑑𝑧
(7.2)
Można scałkować po określeniu funkcji
𝜌 = 𝜌(𝑝) w zależności od zastosowanego modelu atmosfery
ATMOSFERA IZOTERMICZNA
Zależność gęstości od ciśnienia określamy za pomocą równania stanu gazu doskonałego dla
przemiany izotermicznej (T = const), napisanego w postaci:
𝑝
𝜚
=
𝑝
1
𝜚
1
= 𝑅𝑇 = 𝑅𝑇
1
(7.3)
Gdzie R (stała gazowa),
𝜌
1
, 𝑝
1
, 𝑇
1
to parametry gazu na wysokości
𝑍
1
, stąd
𝜚 =
𝜚
1
𝑝
1
𝑝
(7.4)
Uwzględniając (7.4) i (7.2) otrzymamy:
𝑑𝑝 = −𝑔
𝜌
1
𝑝
1
𝑝𝑑𝑧
(7.5)
A po rozdzieleniu zmiennych
𝑑𝑧 = −
𝜚
1
𝛾
1
𝑑𝑝
𝜚
(7.6)
I po scałkowaniu powyższej zależności po warunku brzegowym
𝜌(𝑍
1
) = 𝜌
1
uzyskamy:
𝑍 − 𝑍
1
=
𝜚
1
𝛾
1
𝑙𝑛
𝜚
1
𝑝
(7.7)
Korzystając z
𝑝
2
= 𝑝 = −𝛾𝑉 otrzymamy ostatecznie
𝑝
𝑝
1
=
𝜚
𝜚
1
= 𝑒𝑥𝑝 −
𝛾
1
𝜚
1
𝑍 − 𝑍
1
= 𝑒𝑥𝑝 −
𝜚 𝑍−𝑍
1
𝑅𝑇
1
(7.8)
Wzór (7.8) nosi nazwę wzoru barometrycznego. Dla
𝑍, 𝑝, 𝜌 → ∞ atmosfera izotermiczna rozciągałaby
się na wysokość nieskończoną od powierzchni ziemi
ATMOSFERA O LINIOWYM SPADKU TEMPERATURY
Również w tym przypadku powietrze potraktujemy, jako gaz doskonały, a zgodnie z przyjętymi
warunkami zachodzącymi w troposferze przyjmujemy, że temperatura zmienia się z wysokością według
zależności
𝑇 = 𝑇
0
− 𝜆𝑍
(7.9)
Z równania stanu gazów otrzymamy zależność na gęstośc z funkcją ciśnienia i wysokości
𝜚 =
𝑝
𝑅 𝑇
0
−𝜆𝑍
(7.10)
Po podstawieniu do (7.2) i rozdzieleniu zmiennych daje to równanie
dϱ
ϱ
=
−gdZ
R T
0
−λZ
(7.11)
Po scałkowaniu i wykorzystaniu warunku brzegowego
𝑝 0 = 𝑝
0
otrzymamy
𝜚
1
𝜚
= 1 +
𝜆
𝑇
0
𝑍
𝑔
𝜆𝑅
(7.12)
ATMOSFERA WZORCOWA
Model atmosfery wzorcowej (obowiązującej w lotnictwie) przedstawia zmienność fizykalnych
parametrów przy założeniach:
Powietrze jest gazem o stałej gazowej
𝑅 = 287,14
𝐽
𝑘𝑔𝐾
Na poziome morza powietrze ma parametry:
𝑝 = 𝑝
0
= 760 𝑚𝑚𝐻𝑔 = 1013 ℎ𝑃𝑎
𝑡 = 𝑡
0
= 15
𝑜
,
0
𝑜
𝐶 = 237,15𝐾
𝜚 = 𝜚
0
= 1,2255
𝑘𝑔
𝑚
3
Przyśpieszenie ziemskie nie zależy od wysokości w zakresie
0 ≤ 𝑍 ≤ 20000 𝑚 i jest równe
𝑔 = 9,80665
𝑚
𝑠
2
Do
11000 𝑚 temperatura zmienia się liniowo i osiąga wartość 𝑇
11
= −56,5
𝑜
𝐶
Powyżej
11000 𝑚 jest stała temperatura i wynosi 𝑇
11
Uwzględniając powyższe założenia w zależność (7.9) otrzymujemy zależność na rozkład temperatury
za zmiana wysokości w modelu atmosfery wzorcowej
𝑇 = 288,15 − 0,0065𝑧 𝐾
𝑡 = 15 − 0,0065𝑧 𝐶
𝑜
Oraz na rozkład ciśnienia i gęstości dla
𝑧 ≤ 11000 𝑚
𝑝
𝑝
𝑜
= 1 −
2
44330
5,2543
𝜚
𝜚
𝑜
= 1 −
2
44330
4,2543
i dla
𝑧 ≥ 11000 𝑚
𝑝
𝑝
11
=
𝜚
𝜚
11
= 𝑒𝑥𝑝 −
𝑧 − 11000
6337
Powyższe trzy zależności umożliwiają określenie podstawowych parametrów atmosfery wzorcowej