WYDZIAŁ ELEKTRONIKI TELEKOMUNIKACJI I INFORMATYKI KATEDRA MIERNICTWA ELEKTRONICZNEGO LABORATORIUM PODSTAW MIERNICTWA GRUPA 4A |
||
Ćwiczenie nr 1 |
Imię i nazwisko |
informatyka |
|
Data wykonania ćwiczenia |
2 marzec 99 |
Podstawowe mierniki |
Data odbioru sprawozdania |
10 marzec 99 |
i pomiary elektryczne |
Ocena zaliczenia |
|
|
Uwagi i podpis
|
|
1. Protokół pomiarów
6.4.2. Wzorcowanie woltomierza
Tabela 6.1
Ub [V] |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
Uw [V] |
0.500 |
0.999 |
1.490 |
1.983 |
2.477 |
ε [mV] |
0 |
1 |
10 |
17 |
23 |
δ [%] |
0,000 |
0,100 |
0,667 |
0,850 |
0,920 |
6.4.3. Pomiar rezystancji wewnętrznej woltomierza metodą podstawiania (przed włączeniem zasilania rezystor dekadowy ustawić na Rmax !)
Iw = 0.490mA, Rd = Rv = 50510Ω.
6.4.4. Zmiana zakresu pomiarowego woltomierza
Rd = Rp = 51700Ω.
Tabela 6.2
Ub [V] |
1 |
2 |
3 |
4 |
5 |
Uw [V] |
1.011 |
2.005 |
3.012 |
3.991 |
4.993 |
ε [mV] |
11 |
5 |
12 |
9 |
7 |
δ [%] |
1,100 |
0,250 |
0,400 |
0,225 |
0,140 |
6.4.5. Pomiary miliamperomierzem magnetoelektrycznym
Tabela 6.3
Ib [mA] |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
75 |
Iw [mA] |
10.28 |
20.11 |
30.20 |
40.29 |
50.70 |
60.61 |
70.29 |
75.33 |
ε [μA] |
280 |
110 |
200 |
290 |
700 |
610 |
290 |
330 |
δ [%] |
2,800 |
0,550 |
0,667 |
0,725 |
1,400 |
1,017 |
0,414 |
0,440 |
6.4.6. Pomiary omomierzem (przed włączeniem zasilania rezystor dekadowy ustawić na Rmax !)
Tabela 6.4
α/αmax |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
Rw [Ω] |
0 |
280.0 |
620.0 |
1080.0 |
1680.0 |
2510.0 |
3750.0 |
5800.0 |
9890.0 |
21600.0 |
Tabela 6.5
|
Rw |
+ ΔRw |
− ΔRw |
+ ΔRw Rw |
− ΔRw Rw |
0.1 |
21600.0 |
5500,0 |
3700,0 |
0,255 |
0,171 |
0.5 |
2510.0 |
190,0 |
180,0 |
0,076 |
0,072 |
0.9 |
280.0 |
60,0 |
70,0 |
0,214 |
0,250 |
6.4.7.1. Pomiary napięcia z wykorzystaniem funkcji pamiętania wyniku oraz wartości maks. i min.
Um = 9,995V.
Tabela 6.6
Tryb pracy |
Wskazania multimetru |
|
1 |
Normalny |
Na bieżąco reaguje na zmianę napięcia |
2 |
Pamiętania |
Zapamiętuje obecny wynik i ignoruje następne |
3 |
pamiętania maks. |
Wyświetla tylko większe napięcia od zapamiętanego, mniejsze ignoruje |
4 |
pamiętania min. |
Wyświetla tylko mniejsze napięcia od zapamiętanego, większe ignoruje |
6.4.7.2. Pomiar rezystancji w trybie normalnym i przyrostowym
Tabela 6.7
Nr rezystora |
1 |
2 |
3 |
4 |
5 |
Ri [kΩ] |
8,150 |
8,088 |
8,016 |
8,140 |
8,077 |
ΔRi [kΩ] |
0 |
-0,062 |
-0,132 |
-0,010 |
-0,083 |
Ri'= R1 + ΔRi [kΩ] |
8,150 |
8,088 |
8,018 |
8,140 |
8,067 |
6.5 Opracowanie wyników
6.5.1
Przykładowe obliczenia:
Tabele 6.1, 6.2, 6.3
Ub = 1.5 V Uw = 1,490V
ε = |1,500-1,490| = 0,010V = 10mV
![]()
Tabela 6.5
α = 0.5 Rw = 2510,0 Ω
-Rw = 2330,0 Ω +Rw = 2700,0 Ω
![]()
![]()
+ΔRw = 2510,0-2330,0 = 180 Ω - ΔRw = 2700,0-2510,0 = 190 Ω
Tabela 6.7
R1 = 8,150 kΩ ΔR3= -0,062kΩ R3'= R1+ΔR3=8,150-0,062 = 8,018kΩ
6.5.2.
Interpretacja wykresów.
Wzorcowanie woltomierza zarówno w wersji podstawowej jak i z rozszerzonym zakresem pomiarowym przebiegło zgodnie z oczekiwaniami. Nie stwierdziłem żadnych większych odchyłek w porównaniu ze wskazaniami woltomierza wzorcowego. Woltomierz posiadał klasę dokładności 2, więc max. błąd to 2%. Największy zaobserwowany błąd względny (1,088%) mieści się jeszcze w dopuszczalnej normie. Nieco gorzej sytuacja wygląda w przypadku amperomierza. Podobnie jak woltomierz, posiadał on klasę dokładności 2. Największy zaobserwowany błąd względny wynosił 2,724% , zatem jest większy niż dopuszcza norma. Chciałbym zwrócić uwagę, że tak duży błąd względny powstał tylko w przypadku jednego pomiaru (pozostałe 7 pomiarów mieści się w normie), co może sugerować wystąpienie błędu przypadkowego lub niewielkiego błędu grubego, np. niedokładnie ustawiony prąd na amperomierzu badanym. Badany amperomierz nie był wyposażony w lusterko, co mogło spowodować błąd paralaksy (nierównoległe patrzenie na przyrząd w czasie odczytywania pomiarów).
6.5.3
W trakcie ćwiczenia zmierzyłem opornik badany i stwierdziłem, że :
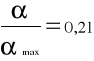
Na podstawie wykreślonej krzywej ustaliłem, że wartość rezystora badanego wynosiła około 9000Ω . Porównując to jednak z wynikami z tabeli 6.7 łatwo zauważyć, że metoda odczytywania rezystancji z wykresu jest bardzo niedokładna. W tym przypadku błąd bezwzględny wynosił około 1000Ω, błąd bezwzględny natomiast 11%. Na tej podstawie stwierdzam, że metoda ta jest raczej mało przydatna do określania rezystancji.
6.5.4
Rezystancja posobnika wyraża się wzorem: Rp = (n-1)RV , przy czym n to mnożnik zakresu pomiarowego.
Skoro rozszerzyłem zakres pomiarowy z 2,5V do 5V to n=5/2,5=2. Podstawiając do wzoru otrzymałem wartość obliczoną posobnika Rp = (2-1)RV = RV = 50510Ω . Eksperymentalnie dobrałem wartość posobnika Rp = 51700Ω. Tak więc rozbieżności pomiędzy nimi wynoszą 1190Ω. Ich przyczyną jest najprawdopodobniej brak możliwości dokładnego stwierdzenia dla jakiej wartości posobnika zakres został rozszerzony dwukrotnie. Mam na myśli fakt, że zmiana rezystancji posobnika o np. 100Ω wywoływała ledwo zauważalną zmianę wychylenia wskazówki.
6.5.5
Przyczyny asymetrii czułości omomierza przy odchyleniach ujemnych i dodatnich w punkcie α/αmax=0,9 można łatwo wyjaśnić nieliniowością wychylenia omomierza w zależności od zmiany rezystancji. Widać to doskonale na krzywej skalowania omomierza.
6.5.6
W związku z tym, że wykonano 5 pomiarów, można zastosować następujące wzory:
Z kolei do wyznaczenia odchylenia standardowego posłużono się wzorem o następującej postaci:
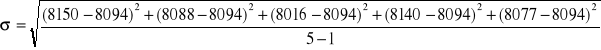
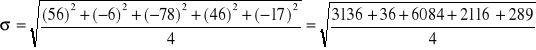
![]()
Odchyłka standardowa wynosi więc 53,99 Ω. Jest to zaledwie 0,6% wartości średniej.
6.5.7
Celem ćwiczenia było zaprojektowanie uniwersalnego miernika elektrycznego o schemacie danych pokazanych na ilustracji:
Iz=1mA kl. 0,5 Rd
+ 50mA 10mA 2mA 1V 5V
200mV
Obliczam Rd :
Uv = RA *IZ = 20mV
![]()
![]()
Obliczam Rw1...Rw3 :
![]()
![]()
![]()
![]()
![]()
![]()
gdzie :
![]()
![]()
![]()
Czyli :
![]()
![]()
![]()
![]()
![]()
![]()
Obliczam Rw4 i Rw5 :
![]()
![]()
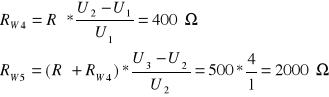
Ostatecznie otrzymałem następujące wartości:
Rd=180Ω RW1=8Ω RW2=32 Ω RW3=160Ω RW4=400Ω RW5= 2000Ω
Strona 1
α/αmax = 0,21
![]()
![]()
![]()
mA
Rw111
Rw2
Rw4
Rw3
Rw5
1=200mV
Rd
Ra=20Ω
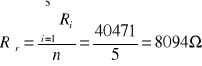
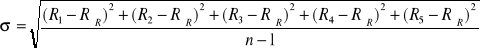
Wyszukiwarka
Podobne podstrony:
1. wzorcowanie, protokol cw1, Laboratorium Podstaw Miernictwa
1. wzorcowanie, protokol cw1, Laboratorium Podstaw Miernictwa
bledy syst przyp, BS I P, Laboratorium Podstaw Miernictwa
NO3 POM CZESTOTLI FAZY, MAR3, LABORATORIUM PODSTAW MIERNICTWA
Laboratorium z podstaw Miernictwa Elektronicznego4
NO6 RLC MOSTKI, MR6 OPR, LABORATORIUM PODSTAW MIERNICTWA
3. pomiar częstotliwości fazy, protokol cw3, Laboratorium Podstaw Miernictwa
NO2 POM OSCYLOSKOPOWE, MR2 OPR, LABORATORIUM PODSTAW MIERNICTWA
2. pomiary oscyloskopowe, protokol cw2, Laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego4 (1)
NO3 POM CZESTOTLI FAZY, MR3 OPR, LABORATORIUM PODSTAW MIERNICTWA
Sprawozdanie z laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego6
Laboratorium z podstaw Miernictwa Elektronicznego
pom nap okr zm 1, Informatyka, Podstawy miernictwa, Laboratorium
pom mocy ukl trojfaz, Informatyka, Podstawy miernictwa, Laboratorium
pom czestot, Informatyka, Podstawy miernictwa, Laboratorium
więcej podobnych podstron