LABORATORIUM PODSTAW MIERNICTWA
ĆWICZENIE NR 3
POMIARY CZĘSTOTLIWOŚCI I FAZY
Patryk Wołowicz EiT sem 2
POMIAR CZĘSTOTLIWOŚCI POPRZEZ POMIAR OKRESU
Pomiaru tą metodą dokonałem wykorzystując proste przekształcenie:
gdzie DtX :czułość kanału; XT :długość okresu na ekranie oscyloskopu.
Ćwiczenie przeprowadzałem używając generatora PO-21 o częstotliwości 2 kHz. Poniższa tabela obrazuje uzyskany wynik:
XT |
cm |
5,1 |
DtX |
ms/cm |
0,1 |
fX |
Hz |
1961 |
δfX |
% |
1,989 |
Otrzymany wynik charakteryzuje się stosunkowo małym błędem względnym, jednak metoda ta nie nadaje się do bardzo dokładnych pomiarów.
2.POMIAR CZĘSTOTLIWOŚCI METODĄ FIGUR LISSAJOUS
Wykorzystałem generator mocy PO-21 o regulowanej częstotliwości od 200 Hz do 800 Hz oraz generator PW-12 o częstotliwości 400 Hz.Regulujac częstotliwość generatora mocy obserwowałem powstające figury i obliczałem liczby przecięć prostych z tymi figurami. Częstotliwość obliczałem ze wzoru:
gdzie fwz= 400 Hz.
PX |
PY |
n |
fmoc [Hz] |
4 |
2 |
0,5 |
200 |
6 |
4 |
0,666 |
266,6 |
4 |
3 |
0,75 |
300 |
2 |
2 |
1 |
400 |
3 |
4 |
1,333 |
533,3 |
2 |
3 |
1,5 |
600 |
4 |
7 |
1,75 |
700 |
2 |
4 |
2 |
400 |
Dla dwóch częstotliwości zaobserwowałem następujące figury:
f=200 Hz
natomiast dla f= 800 Hz
OSYLOSKOPOWE POMIARY KĄTA PRZESUNIĘCIA FAZOWEGO.
W ćwiczeniu wykorzystałem generator o częstotliwości 1 kHz, który podawał sygnał na dwa kanały, natomiast przesunięcia jednego kanału względem drugiego dokonywał czwórnik RC o parametrach 1kΩ i 240 nF.
Zgodnie z przewidywaniami teoretycznymi przesunięcie fazowe w takim dwójniku powinno wynosić:
tan(ϕ) = -ωRC= -2πfRC= -1,50796, czyli ϕ=-56,449°
Pomiar przesunięcia fazowego oscyloskopem dwukanałowym.
Tym razem wykorzystuje się następującą proporcję:
XT |
cm |
7,4 |
Xτ |
cm |
1,2 |
ϕ |
° |
± 58,378 |
δϕ |
% |
3,304 |
Pomiar przesunięcia fazowego metodą figur Lissajous.
Pomiar fazy dokonuje wykorzystując następujący wzór:
2Xm |
cm |
4,8 |
2X0 |
cm |
4,0 |
ϕ |
° |
± 56,443 |
δϕ |
% |
0,011 |
Jak widać metoda wykorzystująca figury Lissajous okazała się o dwa rzędy wielkości dokładniejsza od metody wykorzystującej oscyloskop dwukanałowy. Błąd nie przekracza 0,015 %, a więc właściwie jest do zaniedbania.
POMIAR CZĘSTOTLIWOŚCI Z RĘCZNYM LUB AUTOMATYCZNYM WYBOREM ZAKRESU POMIAOWEGO.
Ręczny wybór zakresu pomiarowego.
Pomiaru dokonywałem podając na częstotliwościomierz PFL-30 sygnał 10000 Hz z generatora PW-12.
Obserwowałem wskazania przyrządu oraz kontrolowałem jego przepełnienie. Jak widać przy pomiarach 10- i 100-sekundowych wystąpiło przepełnienie, a przyrząd „obcinał” cyfry najbardziej znaczące.
Błąd dyskretyzacji obliczałem w/g wzoru:
i malał wraz ze wzrostem czasu pomiaru.
Tp |
s |
10-3 |
10-2 |
10-1 |
1 |
10 |
100 |
stan licznika |
|
11 |
10,1 |
10,01 |
10004 |
0003,7 |
0003,8 |
jednostka |
kHz/Hz |
kHz |
kHz |
kHz |
Hz |
Hz |
Hz |
przepełnienie |
tak/nie |
nie |
nie |
nie |
nie |
tak |
tak |
fX |
Hz |
11000 |
10100 |
10010 |
10004 |
10003,7 |
10003,8 |
δdyskr. |
% |
10 |
1 |
0,1 |
0,01 |
0,001 |
0,0001 |
Pomiar z automatycznym przełączaniem zakresów.
Dla częstotliwości generatora zmieniającej się od 10kHz do 100kHz obserwowałem, kiedy nastąpi automatyczna zmiana zakresu pomiarowego. Zauważyłem, że ma to miejsce dla częstotliwości fgr=80000 Hz.
Na tej podstawie stwierdzam, że w trybie automatycznego wyboru zakresu pomiarowego częstościomierz PFL-30 dokonywał zmiany, gdy wskazania przekraczały 0,8 aktualnego zakresu.
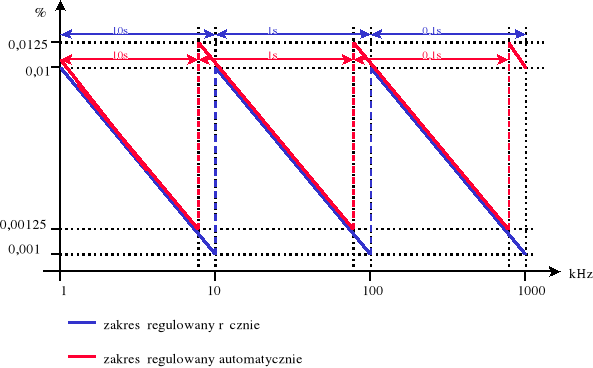
Wykres względnego błędu pomiaru częstotliwości.
Wykres ten wykonany jest w skali logarytmiczno-logarytmicznej i zawiera błąd zarówno dla pomiarów z automatycznym jak i z ręcznym przełączaniem zakresów.
Błąd dostrojenia częstotliwości przyjąłem za stały i równy dla miernika PFL-30 około 0,5*10-6.
Pomiar minimalnego napięcia wejściowego.
Zmniejszając skokowo napięcie wyjściowe generatora podawane na wejście częstościomierza zauważyłem, że wskazania stają się nieprawidłowe dla zakresu 0,1V.
Wykorzystując płynną regulację napięcia określiłem minimalne napięcie wejściowe częstościomierza PFL-30:
Umin=230 mV.
CYFROWY POMIAR STABILNOŚCI CZĘSTOTLIWOŚCI DRGAŃ GENERATORA RC.
Badanym generatorem było urządzenie typu KZ-1403 przy ustalonej częstotliwości 100kHz. Ćwiczenie polegało na przeprowadzeniu dwóch serii pomiarów z kilkuminutowym odstępem czasu. Poniższa tabela zawiera wyniki:
|
Seria I |
Seria II |
Nr |
fX [Hz] |
fX [Hz] |
1 |
102538,6 |
102104,9 |
2 |
102433,1 |
102097,5 |
3 |
102318,2 |
102084,0 |
4 |
102287,7 |
102078,1 |
5 |
102247,8 |
102068,6 |
6 |
102215,4 |
102064,7 |
czas rej. |
14:05 |
14:15 |
Na podstawie tej tabeli mogę wyznaczyć krótkoterminową i długoterminową niestabilność generatora.
Niestabilność krótkoterminowa.
gdzie:
fmax,fmin: maksymalna / minimalna częstotliwość serii;
fnom: częstotliwość generatora.
Dla serii pierwszej:
0,003232,
natomiast dla serii drugiej:
0,000402.
Jak widać krótkoterminowa niestabilność generatora maleje wraz z upływem czasu. Już po kilku minutach jest prawie 10 razy mniejsza.
Niestabilność długoterminowa.
gdzie:
: średnie arytmetyczne częstotliwości w dwóch seriach;
fnom: częstotliwość generatora.
Otrzymałem następujący wynik:
0,01543.
BADANIE PRZETWORNIKA F/U MULTIMETRU M-4650.
Przetwornik F/U zamienia częstotliwość na napięcie z błędem nie przekraczającym 5%.
Oprócz multimetru w poleceniu wykorzystałem częstościomierz PFL-30 oraz generator PW-12. Regulując częstotliwość generatora odczytywałem wskazania z obu mierników.
fg |
fX (M-4650) |
fwz (PFL-30) |
dfx |
kHz |
kHz |
kHz |
% |
10 |
11,03 |
11,006 |
0,2176 |
20 |
21,06 |
21,009 |
0,2422 |
50 |
51,12 |
51,018 |
0,1995 |
80 |
81,08 |
80,95 |
0,1603 |
100 |
101,12 |
100,91 |
0,2077 |
120 |
121,28 |
120,87 |
0,3381 |
140 |
141,96 |
140,85 |
0,7819 |
160 |
162,33 |
160,81 |
0,9364 |
180 |
182,69 |
180,77 |
1,051 |
195 |
197,9 |
195,68 |
1,1218 |
Dodatkowo zamieszczam poniżej wykres liniowo-logarytmiczny względnego błędu przetwornika F/U względem częstotliwości:
Na podstawie wykresu mogę stwierdzić, że najmniejszy błąd przetwornika występuje dla częstotliwości ok. 80kHz, by powyżej 100kHz gwałtownie narastać.
Wyszukiwarka
Podobne podstrony:
3. pomiar częstotliwości fazy, protokol cw3, Laboratorium Podstaw Miernictwa
NO3 POM CZESTOTLI FAZY, MAR3, LABORATORIUM PODSTAW MIERNICTWA
NO3 POM CZESTOTLI FAZY, po czesto i fazy tabele, Mierniki 3. Wst˙p.
NO2 POM OSCYLOSKOPOWE, MR2 OPR, LABORATORIUM PODSTAW MIERNICTWA
NO3 POM CZESTOTLI FAZY, LABMIER3, Damian grupa
NO6 RLC MOSTKI, MR6 OPR, LABORATORIUM PODSTAW MIERNICTWA
bledy syst przyp, BS I P, Laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego4
NO1 WZORCOWANIE, thom1b, Laboratorium Podstaw Miernictwa
1. wzorcowanie, protokol cw1, Laboratorium Podstaw Miernictwa
1. wzorcowanie, protokol cw1, Laboratorium Podstaw Miernictwa
2. pomiary oscyloskopowe, protokol cw2, Laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego4 (1)
Sprawozdanie z laboratorium Podstaw Miernictwa
Laboratorium z podstaw Miernictwa Elektronicznego6
Laboratorium z podstaw Miernictwa Elektronicznego
pom czestot, Informatyka, Podstawy miernictwa, Laboratorium
pom nap okr zm 1, Informatyka, Podstawy miernictwa, Laboratorium
więcej podobnych podstron