POLITECHNIKA POZNAŃSKA INSTYTUT ELEKTROTECHNIKI PRZEMYSŁOWEJ Zakład Podstaw Elektrotechniki |
|||
Laboratorium Podstaw Elektrotechniki Ćwiczenie nr 8 Temat: Układy trójfazowe symetryczne |
|||
Rok akademicki: II Wydział Elektryczny Studia dzienne magisterskie Nr grupy: E 5 |
Wykonawcy:
|
Data |
|
|
|
Wykonania ćwiczenia |
Oddania sprawozdania |
|
|
23.11.2006 |
30.11.2006 |
|
|
Ocena: |
|
Uwagi:
|
|||
1. Wiadomości teoretyczne.
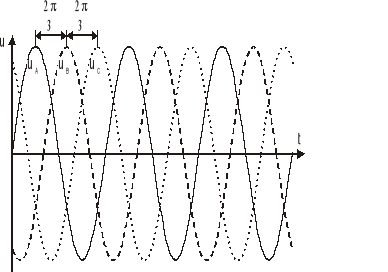
Układem trójfazowym nazywamy zbiór obwodów elektrycznych, w których działają trzy napięcia źródłowe sinusoidalne jednakowej częstotliwości, przesunięte względem siebie w fazie. Zbir napięć i prądów układu trójfazowego nazywamy trójfazowym układem napięć i prądów. Poszczególne obwody napięć źródłowych nazywamy obwodami fazowymi lub krótko fazami. Do oznaczenia poszczególnych faz stosowane są litery A, B, C, lub L1, L2, L3. Jeżeli fazy układu trójfazowego nie są połączone galwanicznie to taki układ nazywamy nieskojarzonym, w przypadku zaś połączenia tych obwodów otrzymujemy układ trójfazowy skojarzony.
Przyjmując oznaczenia faz A, B, C napięcia mogą być napisane odpowiednio w postaci czasowej i zespolonej:
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
Taki układ napięć nazywamy układem symetrycznym zgodnym.
Ważną cechą tego układu jest spełnienie równania:
![]()
Przebieg napięć układu trójfazowego:
Napięcia źródłowe zazwyczaj łączymy w gwiazdę:
Wspólny punkt trzech faz źródła przy połączeniu w gwiazdę nazywamy punktem zerowym źródła. Napięcie ![]()
, ![]()
, ![]()
nazywamy napięciami fazowymi, natomiast napięcia ![]()
, ![]()
, ![]()
nazywamy napięciami międzyfazowymi lub przewodowymi.
Na podstawie rysunku możemy zapisać dla wartości zespolonych:
![]()
![]()
![]()
Dla układu symetrycznego moduły napięć fazowych są sobie równe
![]()
oraz moduły napięć przewodowych są też sobie równe
![]()
Z wykresu wektorowego łatwo wykazać, że:
![]()
Impedancje obciążenia możemy łączyć w gwiazdę lub w trójkąt. Wspólny punkt trzech faz nazywamy punktem zerowym odbiornika.
a) b) c)
Łączenie źródeł impedancji odbiornika: a) w gwiazdę z przewodem zerowym, b) w gwiazdę bez przewodu zerowego, c) w trójkąt
Napięcia ![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
nazywamy napięciami fazowymi odbiornika. Prądy ![]()
, ![]()
, ![]()
nazywamy prądami przewodowymi, natomiast prądy ![]()
, ![]()
, ![]()
nazywamy prądami fazowymi odbiornika.
Dla odbiornika symetrycznego połączonego w gwiazdę napięcia fazowe odbiornika równają się napięciom fazowym źródła zasilania, a prądy fazowe równają się prądom przewodowym, czyli:
![]()
![]()
można wykazać, że:
![]()
Dla odbiornika symetrycznego połączonego w trójkąt, napięcia fazowe odbiornika równają się napięciom międzyfazowym zasilania, a dla prądów można napisać następujące zależności:
![]()
![]()
![]()
![]()
można wykazać, że:
![]()
Wykresy wektorowe napięć i prądów dla układu symetrycznego przy łączeniu odbiornika:
a) w gwiazdę, b) w trójkąt
Moc w układach trójfazowych symetrycznych.
Dla układów symetrycznych moc czynną pobraną przez odbiornik można obliczyć według wzoru:
![]()
gdzie ![]()
jest kątem fazowym odbiornika jednej fazy.
Wyżej podany wzór jest słuszny niezależny od połączenia odbiornika.
Pomiar mocy w układach trójfazowych
Pomiar mocy jednym watomierzem w układzie czteroprzewodowym.
![]()
gdzie P1 jest wskazaniem watomierza W1
Pomiar mocy jednym watomierzem w układzie trójprzewodowym:
![]()
gdzie P1 jest wskazaniem watomierza W1, a Rwn rezystancją cewki napięciowej watomierza.
Pomiar mocy za pomocą dwóch watomierzy (układ Arona):
2. Przebieg ćwiczenia.
2.1. Pomiary napięć, prądów i mocy czynnej pobranej przez odbiornik połączony w gwiazdę.
2.1.1. Schemat połączeń.
Uf = 40V ; ![]()
; 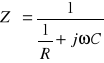
; gdzie: R = 220 ၗ, C = 20 ၭF .
2.1.2.. Przebieg pomiarów.
Połączyliśmy układ według powyższego schematu. Odczytaliśmy wskazania wszystkich mierników w układzie z przewodem zerowym (zamknięty wyłącznik W) oraz w układzie bez przewodu zerowego (otwarty wyłącznik W) dla dwóch przypadków impedancji obciążenia (Z' - połączenie szeregowe R i C; Z” - połączenie równoległe R i
c). Wyniki pomiarów zamieściliśmy w tabeli.
2.1.3. Tabela wyników.
obciążenie |
Rodzaj |
Z pomiarów |
Z obliczeń |
||||||||||||||
|
|
UA |
UB |
UC |
UAB |
UBC |
UCA |
U0 |
IA |
IB |
IC |
I0 |
P1 |
P2 |
P |
tgၪ |
ၪ |
|
|
[V] |
[V] |
[V] |
[V] |
[V] |
[V] |
[V] |
[A] |
[A] |
[A] |
[mA] |
[W] |
[W] |
[W] |
- |
[Ⴐ] |
Z' |
0 |
42 |
42 |
42 |
72 |
72 |
72 |
0 |
0,16 |
0,16 |
0,16 |
- |
5,5 |
11 |
16,5 |
-0,58 |
-30,1 |
|
1 |
42 |
42 |
42 |
72 |
72 |
72 |
- |
0,16 |
0,16 |
0,16 |
0 |
5,5 |
11 |
16,5 |
-0,58 |
-30,1 |
Z” |
0 |
41 |
41 |
41 |
73 |
73 |
73 |
0 |
0,33 |
0,33 |
0,33 |
- |
4 |
22 |
26 |
-1,20 |
-50,2 |
|
1 |
41 |
41 |
41 |
73 |
73 |
73 |
- |
0,33 |
0,33 |
0,33 |
0 |
4 |
22 |
26 |
-1,20 |
-50,2 |
Przykładowe obliczenia pierwszego pomiaru:
![]()
![]()
![]()
2.1.4. Obliczenia.
a) Wykresy wektorowe napięć i prądów dla każdego z pomiarów:
b) Wykazać, który z watomierzy mierzy moc P1 a który P2, jeżeli ![]()
Wykazać to dla wszystkich możliwych wariantów włączenia watomierzy.
Nasz odbiornik miał charakter rezystancyjno- pojemnościowy, kąt przesunięcia fazowego
takiego odbiornika jest ujemny, wiec musi być spełniona równość: P1<P2
Przykładowy schemat układu do pomiaru mocy za pomocą dwóch watomierzy (Układ Arona):
Dla powyższego schematu możemy wykreślić wykres wskazowy napięć i prądów. W tym celu postępujemy następująco: najpierw należy nanieść wskazy napięć źródłowych UA, UB, UC, przesunięte względem siebie w fazie o 120º. Następnie wyznaczamy konstrukcyjnie napięcia międzyfazowe UAB, UBC, UCA, których wskazy wyprzedzają napięcia fazowe o 30º. Watomierz W2 mierzy moc czynną określoną wzorem:
![]()
natomiast watomierz W1:
![]()
.
UCB jest napięciem przeciwnym co do zwrotu i kierunku do napięcia UBC.
Wykres wskazowy dla powyższego układu ma postać:
Interpretując wykres wnioskujemy, że:
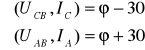
przy czym ϕ - kąt przesunięcia między napięciem a prądem jednej fazy odbiornika
Watomierze wskazują moce:
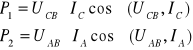
ale IA=IB=I oraz UAB=UBC=U,
przy czym I oraz U są wartościami przewodowymi, odpowiednio, prądu i napięcia w układzie trójfazowym
wiec
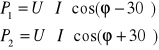
Korzystając z powyższych wzorów po odpowiednim ich przekształceniu otrzymujemy:
![]()
![]()
Wzory trygonometryczne różnicy i sumy kątów:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Podstawiamy:
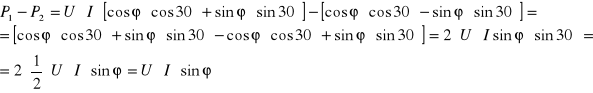
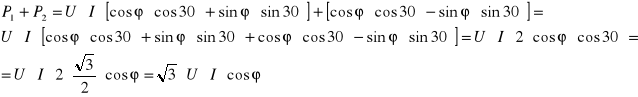
Ze wzoru na różnicę mocy P1 i P2 wyznaczam zależność na sinus kąta ![]()
:
![]()
Ze wzoru na sumę mocy P1 i P2 wyznaczam zależność na kosinus kąta![]()
:
![]()
Teraz podstawiam obliczone zależności do wzoru na ![]()
:
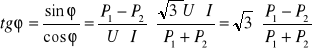
![]()
Czytając przedstawiony powyżej schemat połączeń- układ Arona widzimy, że koniec cewki napięciowej watomierza W1 włączony jest do poprzedniej fazy, a koniec W2 do fazy następnej. Możemy wiec wyciągnąć wniosek, że w powyższym wzorze na tgφ moc P1 zawsze wskazuje watomierz, którego koniec cewki napięciowej włączony jest to poprzedniej fazy, a moc P2 zawsze wskazuje watomierz, którego koniec cewki napięciowej włączony jest do fazy następnej. Zasada ta spełniona jest dla dowolnej konfiguracji układu Arona, które to kombinacje zamieściłem na rysunku poniżej:
c) Obliczyć teoretycznie kąt fazowy odbiorników stosowanych w ćwiczeniu i porównać go z kątem fazowym wyznaczonym doświadczalnie.
Wartości pojemności kondensatorów C1, C2, C3 oraz rezystancji R1, R2, R3 użytych w naszym ćwiczeniu zmierzyliśmy multimetrem cyfrowym, a wyniki pomiarów były następujące:
R1=218,09 Ω; R1=214 Ω; R1=217,66 Ω;
C1=20,12 μF; C2=20,29 μF; C3=20,11 μF;
Rezystancja i pojemność średnia wynoszą:
![]()
![]()
Obliczam impedancję obciążenia Z'(połączenie szeregowe R z C):
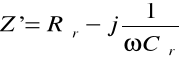
gdzie ![]()
![]()
Z obliczeń wynika, że kąt fazowy ![]()
.
Impedancja obciążenia Z'(połączenie równoległe R z C):
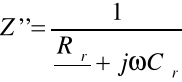
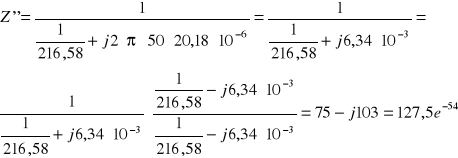
Dla tego przypadku kąt fazowy ![]()
.
2.2. Pomiary napięć, prądów i mocy czynnej pobieranej przez odbiornik połączony w trójkąt.
2.2.1. Schemat połączeń.
Up =![]()
V ; ![]()
; 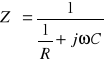
; gdzie: R = 220 ၗ , C = 20 ၭF .
2.2.2. Przebieg pomiarów.
Połączyliśmy układ według powyższego schematu. Odczytaliśmy wskazania wszystkich mierników dla dwóch przypadków impedancji obciążenia (Z' - połączenie szeregowe R i C; Z” - połączenie równoległe R i C).
2.2.3. Tabela wyników.
Obciążenie |
Z pomiarów |
Z obliczeń |
||||||||||||
|
UAB |
UBC |
UCA |
IA |
IB |
IC |
IAB |
IBC |
ICA |
P1 |
P2 |
P |
tgၪ |
ၪ |
|
[V] |
[V] |
[V] |
[A] |
[A] |
[A] |
[A] |
[A] |
[A] |
[W] |
[W] |
[W] |
- |
[Ⴐ] |
Z' |
72 |
72 |
72 |
0,47 |
0,47 |
0,47 |
0,27 |
0,27 |
0,27 |
15 |
33 |
45 |
-0,65 |
-33 |
Z” |
72 |
72 |
72 |
0,98 |
0,98 |
0,98 |
0,57 |
0,57 |
0,57 |
10 |
64 |
74 |
-1,27 |
-52 |
Przykładowe obliczenia pierwszego pomiaru:
![]()
![]()
![]()
2.1.4. Obliczenia.
Wykresy wektorowe napięć i prądów dla każdego z pomiarów:
b) Wykazać, który z watomierzy mierzy moc P1 a który P2, jeżeli ![]()
.
Wykazać to dla wszystkich możliwych wariantów włączenia watomierzy.
Obliczenia jakie wykonałem w podpunkcie b) dla odbiornika połączonego w gwiazdę są
również słuszne dla połączenia w trójkąt. Tok postępowania przy wyprowadzaniu wzoru na ![]()
jest identyczny w obu przypadkach.
c) Obliczyć teoretycznie kąt fazowy odbiorników stosowanych w ćwiczeniu i porównać go z kątem fazowym wyznaczonym doświadczalnie.
Obliczenia dla tego podpunktu są identyczne jak dla punktu c) przy połączeniu odbiornika w gwiazdę.
3. Wnioski i uwagi końcowe.
a) Do pomiaru mocy czynnej w powyższym ćwiczeniu wykorzystaliśmy metodę dwóch watomierzy zwaną inaczej metodą Arona.
Moce czynne wskazywane przez watomierze W1, W2 można przedstawić w postaci:
Dodając oba wyrażenia otrzymujemy:
Jeżeli odbiornik połączony jest w gwiazdę to wtedy obowiązują zależności:
Z tego wynika, że moc całkowitą można wyliczyć korzystając ze wzoru:
W podobny sposób można wykazać, że metodą dwóch watomierzy można wyznaczyć moc czynną wydzieloną na odbiorniku połączonym w trójkąt.
Gdy |ϕ| > 60°, wówczas na podstawie poniższych wzorów:
przy czym U, I - wartości skuteczne napięcia międzyfazowego i prądu przewodowego odbiornika.
Jedna z wielkości P1, P2 jest ujemna. Wbrew naszym domysłom wskazania ujemnej wartości mocy nie powodują odchylenia wskazówki watomierza w przeciwną stronę. Przyrządy te są zbudowane tak, że ich wskazówka może odchylać się tylko w jedną stronę. W celu odczytania ujemnych wskazań należy zmienić zwrot prądu w cewce napięciowej watomierza. Wówczas otrzymamy właściwe odchylenie wskazówki watomierza, jednakże należy traktować to wskazanie jako wielkość ujemną.
b) Przy połączeniu odbiornika w gwiazdę prądy przewodowe i fazowe są sobie równe, a napięcia międzyfazowe są o ![]()
większe od napięć fazowych.
Przy połączeniu w trójkąt jest inaczej. Napięcia fazowe i międzyfazowe są sobie równe, natomiast prądy fazowe są o ![]()
większe od prądów fazowych. Aby wyznaczyć wartości prądów przewodowych, korzystamy z pierwszego prawa Kirchhoffa.
Przy niezmiennym układzie zasilania po przełączeniu z gwiazdy w trójkąt prądy przewodowe wzrosną o ![]()
, tak samo wzrasta napięcie na poszczególnych fazach, a całkowita moc wzrosła niemalże 3-krotnie.
Wnioskujemy stąd, że jeśli odbiornik połączony jest w gwiazdę to pobiera 3-ktornie mniej energii ze źródła. W praktyce jest to wykorzystywane przy rozruchu silników indukcyjnych większych mocy.
c) Porównując kąty fazowe odbiornika połączonego w gwiazdę, obliczone analitycznie (w podpunkcie c) pierwszej części zadania) oraz wyznaczone doświadczalnie nasuwają się nam następujące wnioski:
kąt fazowy odbiorników, uzyskany na podstawie obliczeń teoretycznych w podpunkcie pierwszym 1) wynosi ![]()
, w drugim 2)![]()
natomiast wartość tego kąta wyznaczona doświadczalnie odpowiednio dla Z'![]()
, a dla Z'' ![]()
. Różnica pomiędzy kątami obliczonymi, a zmierzonymi doświadczalnie jest duża, ponieważ ![]()
dla pierwszego przypadku oraz ![]()
w przypadku drugim. Moim zdaniem błędy te są skutkiem mało precyzyjnego odczytu przez nas wskazań przyrządów oraz niedokładności przyrządów pomiarowych.
Interpretujemy wyniki uzyskane dla połączenia trójkątnego, mianowicie:
kąt fazowy dla połączenia szeregowego R i C (Z') uzyskany na drodze doświadczalnej wynosi![]()
, dla połączenia równoległego (Z'') ![]()
. Po porównaniu tych wyników z obliczeniami analitycznymi uzyskujemy następujące różnice: dla Z' ![]()
, a dla Z'' ![]()
. Wartości tych błędów są mniejsze, aniżeli błędów dokonanych przy pomiarach dla układu połączenia odbiornika w gwiazdę.
W brudnopisie załączonym do tego sprawozdania, w tabeli pomiarowej zawierającej wyniki pomiarów dla odbiornika połączonego w gwiazdę przy połączeniu równoległym rezystora i kondensatora (Z'') popełniliśmy błąd, a mianowicie wyniki pomiarów napięć międzyfazowych wpisaliśmy w rubryki przeznaczone dla napięć fazowych i odwrotnie. Oczywistym jest, że napięcia międzyfazowe dla odbiornika połączonego w gwiazdę są o ![]()
większe od napięć fazowych, dlatego w tabeli sprawozdania uwzględniłem to niedopatrzenie i naniosłem odpowiednią poprawkę.
4. Parametry i dane znamionowe zastosowanych urządzeń i mierników.
- płytka pomiarowa „Układy trójfazowe” 220Ω 20μF
- 2 watomierze analogowe
- amperomierz analogowy 0,6 - 30 A
- amperomierz analogowy 1 - 2 A
- woltomierz analogowy 75 V 150 V
- multimetr cyfrowy
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
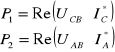
Wyszukiwarka
Podobne podstrony:
Układy trójfazowe niesymetryczne - j, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Labor
3-fazowka Miko, układy 3-faz. niesymetryczne 2, POLITECHNIKA POZNAŃSKA
10. Układy trójfazowe symetryczne matej, POLITECHNIKA POZNAŃSKA
układy trójfazowe, Politechnika Opolska, sprawozdania, zachomikowane, teoria obwodów
Falownik-sprawko, Politechnika Poznańska (PP), Elementy i układy automatyzacji maszyn, Laboratorium,
badania silnika indukcyjnego trójfazowego, Politechnika Poznańska (PP), Elektronika i elektrotechnik
Sprawozdanie Silniki, Politechnika Poznańska (PP), Elektronika i elektrotechnika, Labolatoria, Ćw 6
09-rozruch i hamowanie silników asynchronicznych trójfazowych, Politechnika Poznańska (PP), Elektron
uklady zasilajace, Politechnika Poznańska, Mechatronika, Semestr 04, Projektowanie układów elektroni
MO - sprawozdanie 2(1), Politechnika Poznańska, Mechatronika, SEMESTR I, Odlewnictwo
egz TRB I 2009 c, Politechnika Poznańska, Budownictwo, Technologia Robót Budowlanych, Zaliczenie wyk
KONWENCJA BERNEŃSKA, MiBM Politechnika Poznanska, VII semestr TPM, Ochrona Własności Intelektualnej,
03 - Pomiar twardości sposobem Brinella, MiBM Politechnika Poznanska, IV semestr, labolatorium wydym
MW zaliczenie, Politechnika Poznańska ZiIP, IV semestr, IV semestr, Techniki pomiarowe, TechnikiPom,
c3 stal po ob ciep-chem, Politechnika Poznańska, Edukacja Techniczno Informatyczna, Semestr II, Mate
Pojęcia, MiBM Politechnika Poznanska, VII semestr TPM, Ochrona Własności Intelektualnej, wojtysiak,
zaliczenie odpowiedzi, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Bud
więcej podobnych podstron