Badania Operacyjne www.pure6.neostrada.pl

Wykład 03 2004-10-25

PROGRAM LINIOWY:

X = (x₁, x₂,…, x_k)

f(X) = c₁x₁ +c₂x₂ +…+ c_kx_k » max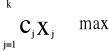

przy warunkach ograniczających:

a₁₁x₁ + a₁₂x₂ + … + a_1kx_k ≤ b₁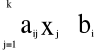
(i=1,…,m)

a₂₁x₁ + a₂₂x₂ + … + a_2kx_k ≤ b₂ x_j ≥ 0 (j=1,…,n)

……………………………………………….

a_m1x₁ + a_m2x₂ + … + a_mkx_k ≤ b_m

x_j ≥ 0 (j=1,…,n)

C^T » max

A_x ≤ b

x ≥ 0

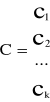
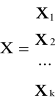
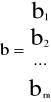
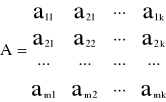
Jest to postać kanoniczna. Komplementarną formą jest postać standardowa.

POSTAĆ STANDARDOWA charakteryzuje się tym, że:

• warunki graficzne zapisane są w postaci równań

• wyrazy wolne poszczególnych warunków ograniczających są nieujemne

• warunki nieujemności są pełne tzn. dotyczą wszystkich zmiennych decyzyjnych

X = (x₁, x₂,…, x_k)

f(X) = c₁x₁ +c₂x₂ +…+ c_nx_n » max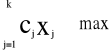

przy warunkach ograniczających:

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n = b₁ b₁ ≥ 0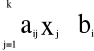
(i=1,…,m)

a₂₁x₁ + a₂₂x₂ + … + a_2kx_k = b₂ b₂ ≥ 0 b_i ≥ 0

…………………………………………. x_j ≥ 0 (j=1,…,n)

a_m1x₁ + a_m2x₂ + … + a_mnx_n = b_m b_m ≥ 0

x_j ≥ 0 (j=1,…,n)

C^T » max A_x ≤ b x ≥ 0 b ≥ 0 C,X Є Rⁿ A_mxn b Є R^m

METODY WYZNACZANIA ROZWIĄZANIA ZADANIA PROGRAMOWANIA LINIOWEGO:

1. metoda graficzna (geometryczna)

2. program dualny

3. metoda Simplex

Warunki stosowalności:

Metodę 1) można stosować tylko wtedy, jeśli w modelu znajdują się 2 zmienne decyzyjne (co najwyżej 3 zmienne). Jeśli w modelu programowania liniowego znajduję się więcej zmiennych decyzyjnych niż 2 (lub 3), natomiast liczba warunków ograniczających wynosi 2 (lub 3), to można wyznaczyć rozwiązanie takiego zadania programowania liniowego korzystając z zapisu programu dualnego w stosunku do programowania pierwotnego.

Metoda Simplex, która jest metodą uniwersalną, polegającą najogólniej biorąc na wyznaczeniu wstępnego rozwiązania bazowego, a następnie poprawianiu tego rozwiązania w kolejnych krokach iteracyjnych aż do uzyskania rozwiązania optymalnego, można stosować do wyznaczenia rozwiązania praktycznie rzecz biorąc każdego modelu PL (za wyjątkiem przypadków degenerowanych)

PROGRAM DUALNY:

Program pierwotny Program dualny

zmaksymalizować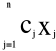
zminimalizować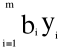

przy warunkach ograniczających: przy warunkach ograniczających:

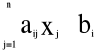
(i=1,…,m)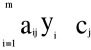
(j=1,…,n)

(j=1,…,n)
(i=1,…,m)

Program dualny jest w pewnym sensie transpozycją programu pierwotnego, a charakter tej transpozycji jest następujący:

1. j - ta kolumna współczynników stojących przy zmiennych decyzyjnych w warunkach ograniczających PP staję się i - tym wierszem współczynników w warunkach ograniczających PD

2. wektor ograniczeń zagadnienia pierwotnego przejmuje rolę współczynników funkcji celu w PD

3. współczynniki funkcji celu PP stają się wektorem wyrazów wolnych w PD

4. rodzaj optymalizacji oraz kierunki nierówności w warunkach ograniczających są przeciwne względem siebie w obu zagadnieniach

TWIERDZENIE 1

Jeżeli zagadnienie pierwotne i dualne mają rozwiązania dopuszczalne a
stanowi rozwiązanie optymalne zagadnienia pierwotnego, natomiast
stanowi rozwiązanie optymalne zagadnienia dualnego, to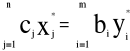
, co oznacza, że wartość funkcji celu zagadnienia pierwotnego i dualnego jest taka sama.

TWIERDZENIE 2

Jeżeli program pierwotny (dualny) ma skończone rozwiązanie optymalne to adekwatnie do niego program dualny (pierwotny) ma również rozwiązanie optymalne o tej samej wartości funkcji celu.

---