Wydział Inżynierii

Środowiska i Energetyki

Grupa 3

Rejestracja składowej przenikliwej promieniowania kosmicznego.

Sekcja 4

Mariusz Czaja

1.Wstęp teoretyczny.

We wnętrzu gwiazd w tym również Słońca, zachodzą nieustannie liczne reakcje jądrowe, a w ich rezultacie w przestrzeń kosmiczną wysyłane są kwanty X i γ , protony, jądra ciężkich pierwiastków oraz inne cząstki. Strumień tych cząstek jest określany nazwa promieniowania kosmicznego. Składowa korpuskularna promieniowania kosmicznego, docierająca do górnych warstw atmosfery Ziemi, składa się głównie z protonów (około 84%) oraz cząstek α (około15%) o bardzo dużych energiach, zawierających się w przedziale od 1GeV do 1000GeV. Promieniowanie to zwane jest pierwotnym promieniowaniem kosmicznym. Powoduje ono jonizację górnych warstw atmosfery, a ponadto inicjuje liczne reakcje jądrowe z udziałem jąder pierwiastków wchodzących w skład atmosfery Ziemi. W rezultacie tych reakcji powstaje wtórne promieniowanie kosmiczne, w którym wyróżnia się tzw. składowa twardą (zwaną też przenikliwą) oraz składową miękką. Maksymalne natężenie promieniowania kosmicznego występuje w przedziale wysokości od 20 do 40 km nad poziomem morza, a następnie szybko maleje osiągając na poziomie morza wartość dwudziestokrotnie niższa.

Składowa miękka promieniowania kosmicznego składa się głownie z elektronów, pozytonów oraz kwantów promieniowania elektromagnetycznego. Stanowi ona znaczną część promieniowania kosmicznego na poziomie morza. Składowa ta jest silnie pochłaniana, zwłaszcza w ośrodkach o dużych wartościach średniej liczby atomowej Z. Doświadczalnie stwierdzono, że kilkucentymetrowa warstwa ołowiu prawie całkowicie eliminuje składową miękką promieniowania kosmicznego.

Składową przenikliwą wtórnego promieniowania kosmicznego przy powierzchni Ziemi stanowią głownie cząstki zwane mionami. Cząstki te należą do rodziny cząstek elementarnych, zwanych leptonami, do której należą również elektron, pozyton oraz neutrina. Miony są cząstkami naładowanymi dodatnio (μ⁺) lub ujemnie (μ^-). Wielkość ładunku mionu jest równa +e lub -e, masa mionu jest 207 razy większa od masy elektronu. Niska zdolność jonizacyjna mionów w połączeniu z ich wysoką energią jest podstawową przyczyną ich niezwykle dużej przenikliwości. Miony są cząstkami nietrwałymi i rozpadają się na elektron (lub pozyton) oraz neutrina. Średni czas życia mionu jest stosunkowo krótki i wynosi 2,2 μs. Występowanie mionow na powierzchni Ziemi, po przebyciu przez nie drogi ok. 20 km, stanowi potwierdzenie słuszności relatywistycznego wydłużenia czasu. Na poziomie morza przez powierzchnie 1cm² przechodzą w przybliżeniu 2 miony w czasie jednej minuty. Tory większość mionow mają kierunek pionowy lub zbliżony do pionowego. Rozkład kątowy natężenia strumienia mionów można w przybliżeniu opisać zależnością:

I(Φ) = I₀ cos⁴Φ

Φ - kąt między kierunkiem toru mionu a kierunkiem pionowym.

Przebieg ćwiczenia.

1. Wykonujemy po pięć jednominutowych pomiarów liczby zliczeń impulsów

na przemian przy pionowym i poziomym ustawieniu liczników. Błąd

pojedynczego pomiaru jest równy pierwiastkowi z liczby zliczeń:

N ± √ N

2. Wyznaczamy średnie szybkości zliczeń dla poziomego x₁ i pionowego x₂

ustawienia liczników oraz ich błędy:

∆x_i = √x_i / n

3. Sprawdzić, czy wyznaczone średnie szybkości zliczeń są istotnie różne obliczając wartość wyrażenia:

│x₁ - x₂│

√ (∆x₁)² + (∆x₂)²

Mianownik jest błędem szybkości zliczeń. Jeżeli wyrażenie to jest większe

od 3, to można mówić o istotnej (znaczącej) różnicy. Wynik testu

przedstawić prowadzącemu ćwiczenia.

4. Wykonać pięciominutowe pomiary liczby zliczeń impulsów w zależności od

kąta ustawienia liczników względem pionu dla kątów: 0º, 30º, 60º, 90º, 120º,

150º i 180º.

Wyniki przedstawić na wykresie. Na wykresie należy umieścić błędy

pomiarowe.

3. Obliczenia.

Średnie szybkości zliczeń:
n- liczba pomiarów

Pionowe ustawienie liczników:

Poziome ustawienie liczników:

Błędy średnich szybkości zliczeń:
x_i - średnie szybkości zliczeń

Wzór na obliczanie błędu liczby zliczeń impulsów dla pojedynczego pomiaru:

Błędy pojedynczych pomiarów:

[N=(N)±(ΔN)] - sposób podawania wyników w tabelach

Pionowe ustawienie liczników	Poziome ustawienie liczników
N=28 ± 6	N=13 ± 4
N=25 ± 5	N=12 ± 4
N=23 ± 5	N=11 ± 4
N=25 ± 5	N=11 ± 4
N=18 ± 5	N=14 ± 5

Błędy pomiarów dla poszczególnych odchyleń od pionu:

Kąt ustawienia liczników	Liczba zliczeń
0º ± 1º	N=116 ± 11
30º ± 1º	N=106 ± 11
60º ± 1º	N=66 ± 9
90º ± 1º	N=51± 8
120º ± 1º	N=76 ± 9
150º ± 1º	N=100 ± 10
180º ± 1º	N=221 ± 15

Błąd kąta ustawienia liczników wynika z niedoskonałości przyrządu

(kątomierza) i przyjmujemy go Δα=1º

Sprawdzam czy wyznaczone średnie szybkości zliczeń są istotnie różne obliczając wartość wyrażenia: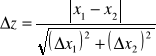

x₁=21

x₂=13

Δx₁=3

Δx₂=2

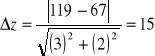
Wyrażenie jest większe od 3 wiec średnie prędkości zliczeń są istotnie różne.

Δz - iloraz modułu z różnicy średniej liczby zliczeń dla poziomego i pionowego ustawienia liczników przez błąd różnicy szybkości zliczeń.

4. Wnioski.

Liczba impulsów odczytywana z licznika Geigera-Müllera przy ustawieniu pionowym i poziomym jest przykładem zdarzeń niezależnych (istotnie różnych). Świadczą o tym duże wartości parametru Δz=15, dla różnicy zliczeń z obydwu ustawień liczników.

Częstotliwości zliczania impulsów dla pionowego ustawienia liczników Geigera-Müllera jest około dwukrotnie większa niż dla ustawienia poziomego.

Dla ustawienia pionowego średnia liczba impulsów wynosi 24 impulsy/min, a dla ustawienia poziomego 13 impulsów /min.

Błędy zliczeń impulsów wahają się od 8 do 14 impulsów (przy pomiarach pięciominutowych) co daje błędy zliczeń rzędu od 6% do 16%. Natomiast przy pomiarach jednominutowych (na przemian ustawienie poziome i pionowe liczników) błędy zliczeń impulsów wahały się od 20% do 36%.

Tak duże błędy świadczą o wysokiej niedokładności pomiaru liczby zliczeń impulsów.

Ze wzoru I=I_o+cos⁴φ wynika, że dla φ=90º , I=0 ( I(φ)-rozkład kątowy natężenia strumienia mionów ). Z przeprowadzonych pomiarów wynika, że dla φ=90, I>0. Oznacza to, że liczniki Geigera-Müllera zbierają impulsy z pewnego zakresu kątów, powodem tego jest różny kąt padania mionów (nie tylko pionowy).

Dodatkowy wykres N=f(α), który jest niesymetryczna parabolą pokazuje, że w liczbie impulsów są pewne nieścisłości, ponieważ teoretycznie wykres N=f(α) jest symetryczną parabolą. Po przeanalizowaniu wyników zauważyłem że, różnice w liczbie zliczeń dla kolejnych kątów są podobne tzn. dla kąta 30º i 60º wynosi ona 32 impulsy i dla równoważnych kątów czyli dla kąta 120º i 150º różnica liczby zliczeń wynosi 30 impulsów. Dla pozostałych kątów zachodzą podobne zależności za wyjątkiem kątów 60º i 90º oraz 90º i 120º gdzie różnica liczby zliczeń wynosi odpowiednio 24º i 44º impulsy. Oznacza to że, dla pierwszej pary kątów liczba zliczeń jest dwa razy mniejsza niż dla drugiej.

Oznacza to, że liczba zliczeń impulsów dla kątów 120º, 150º i 180º jest o ok.

20 impulsów większa niż dla odpowiednich dla nich kątów 0º, 30º i 60º mimo tego, że są one symetrycznie oddalone od poziomu.

Moim zdaniem powodem tego jest wada któregoś z dwóch liczników Geigera-Müllera tzn. obracając liczniki od 0º do 90º jeden z nich jest zawsze wyżej niż drugi lecz gdy obracamy je od 90º do 180º następuje zmiana i ten który był niżej

jest teraz nad tym który był wyżej. Zakładając wadę któregoś licznika może to powodować mylne zliczanie impulsów.

1

---