Rok akademicki 1996/97	Laboratorium z fizyki
Nr ćwiczenia: 72	Zjawisko Halla.
Elektronika telekomunikacja Grupa: E.02	Tomasz Król
Data wykonania	Ocena		Data zaliczenia	Podpis
6.03.1997	T
	S

1.Zasada pomiaru

Zjawisko Halla polega na powstaniu pola elektrycznego E w półprzewodniku, przez który płynie prąd o gęstości j umieszczonym w polu magnetycznym B.

E_H = R_H B x j

Gdy B jest prostopadła do j, to E_H = R_HBj.

gdzie: Fz - siła pochodząca od zew. pola elektrycznego.

R_H - współczynnik Halla.

Powstawanie poprzecznego pola elektrycznego. (pola Halla): uporządkowany ruch elektronów w płytce odbywa się ze średnią prędkością unoszenia V w kierunku prostopadłym do wektora indukcji pola magnetycznego B i wówczas na poruszające się elektrony działa siła Lorentza F_L = -e V x B która przemieszcza je ku jednemu bokowi płytki. W wyniku tego na powierzchniach bocznych płytki powstaje nadmiarowy ładunek:na jednej dodatni, na drugiej ujemny. Powstaje zatem dodatkowe pole elektryczne. skierowane wew. płytki od B do A, o natężeniu: E_H = U_H / a ,

gdzie: U_H - napięcie Halla, różnica potencjałów między punktami A i B,

a - odległość między tymi punktami.

Pole to działa na elektrony siłą F_E= - eE= - eU_H /a przeciwnie skierowaną do siły Lorenyza. Gdy ustali się równowaga, napięcie Halla już nie wzrasta, F_E=F_L.

Z warunku równowagi:

e V B = eU_H /a

otrzymamy

U_H = V B a.

Uwzględniając, że V = -j / ne gdzie: V - średnia prędkość elektronów,

j - gęstość prądu w płytce,

n - koncentracja elektronów (liczba elektronów przewodnictwa w jedn. objętości próbki)

Otrzymamy formułę na napięcie Halla: gdzie:

Stąd stałą Halla wyznaczamy ze wzoru:

Przy znanej stałej Halla można obliczyć koncentrację elektronów swobodnych w metalu lub elektronów przewodnictwa w półprzewodniku zdegenerowanym oraz ich ruchliwość - ruchliwość holowską:

- opór właściwy materiału

2.Schemat układu pomiarowego

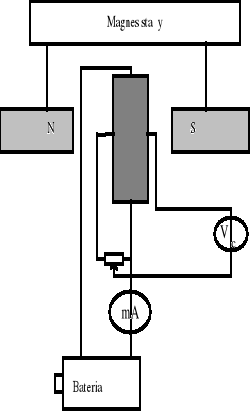
Ocena dokładności pojedynczych pomiarów

W doświadczeniu stosowano urządzenia:

• a) miliamperomierz (K = 0.5 ; Zakres: 30 mA)

woltomierz Digital Voltmeter typeV541 (Zakres: 100mV)

Błąd maksymalny ΔU= 0,05 mV

c) badana próbka - monokryształ Ge:(półprzewodnik typu n)

- długość próbki l = (5 ± 0,1) mm

- grubość próbki b = (2 ± 0,1) mm

- szerokość próbki a = (3 ± 0,1) mm

- oporność właściwa r = 1,5 * 10^-3 Wm

d) magnes o indukcyjności B = (170 ± 7,5) mT

Błąd pomiaru miliamperomierzem obliczyłem ze wzoru

przy czym: K - klasa miernika,

Z - zakres na którym mierzono

ΔX - błąd miernika

Błąd amperomierza więc ΔI = 0,15mA

4.Tabele pomiarowe

Lp.	I	- UH	+ UH	UHśr	UHśr∗I	I^2	UHśr*ΔI	I*ΔUHśr	I*ΔI	UH (teoret)
	[mA]	[mV]	[mV]	[10^2mV]	[μW]	[μA^2]	[μW]	[μW]	[μA^2]	mV
1	2	0,16	0,13	0,145	0,29	4	0,021	0,10	0,30	0,156
2	3	0,23	0,20	0,215	0,65	9	0,032	0,15	0,45	0,233
3	4	0,33	0,27	0,300	1,20	16	0,045	0,20	0,60	0,311
4	5	0,42	0,35	0,385	1,93	25	0,058	0,25	0,75	0,389
5	6	0,50	0,42	0,460	2,76	36	0,069	0,30	0,90	0,467
6	7	0,59	0,49	0,540	3,78	49	0,081	0,35	1,05	0,545
7	8	0,68	0,57	0,625	5,00	64	0,094	0,40	1,20	0,622
8	9	0,77	0,64	0,705	6,35	81	0,106	0,45	1,35	0,700
9	10	0,88	0,73	0,805	8,05	100	0,121	0,50	1,50	0,778
10	11	0,94	0,80	0,870	9,57	121	0,131	0,55	1,65	0,856
11	12	0,95	0,95	0,950	11,40	144	0,143	0,60	1,80	0,934
12	13	1,04	1,03	1,035	13,46	169	0,155	0,65	1,95	1,011
13	14	1,10	1,08	1,090	15,26	196	0,164	0,70	2,10	1,089
14	15	1,21	1,17	1,190	17,85	225	0,179	0,75	2,25	1,168
Δ	0,15	5	5
Σ				9,315	97,55	1239	1,397	5,95	17,85	10,73

Przykładowe obliczenia wyników pomiarów wielkości złożonej

a) Współczynnik kierunkowy prostej α

b) Stała Halla R_H

c) Koncentracja nośników n

d) Ruchliwość nośników ładunku μ

e) U_H teoretyczne

dla I = 2 mA , α = 77,772 *10^-3 mV / mA

U_H = 2 *77,772*10^-3 = 0,156 *10^-3 [mV]

Rachunek błędów

a) Błąd względny współczynnika kierunkowego prostej

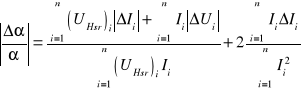
można uprościć do postaci:

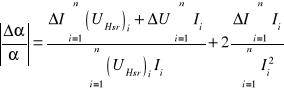
gdyż wszystkie pomiary zostały wykonane przy tych samych zakresach przyrządów.

b) Błąd bezwzględny współczynnika kierunkowego prostej

c) Błąd stałej Halla obliczany metodą różniczki logarytmicznej

d) Błąd bezwzględny koncentracji nośników Δn

Błąd bezwzględny ruchliwości nośników Δμ obliczany metodą różniczki logarytmicznej

Zestawienie wyników pomiarów

a) Współczynnik kierunkowy prostej α

α = ( 0,78 ± 0,07 ) V / A

b) Stała Halla R_H

R_H = ( 0,97 ± 0,19 ) ⋅ 10^-6 m³ / C

c) Koncentracja nośników n

n = ( 6.42 ± 1,24 ) ⋅ 10²⁴ 1 / m³

d) Ruchliwość nośników ładunku μ

μ = ( 6,48 ± 1,25 ) ⋅ 10^-4 s² ⋅ A / kg

Uwagi i wnioski

W doświadczeniu mogą występować duże błędy wynikające z bardzo dużej wrażliwości potencjometru służącego do regulacji prądu. Stosunkowo duży błąd powstały przy obliczaniu stałej Halla (stanowiący aż 20%). Wynika to z pomiaru wielkości próbki albowiem już przy samej grubości (2 μm) mamy do czynienia z 5% błędem oraz błąd współczynnika kierunkowego stanowiący ok. 10%. W znacznym stopniu błąd stałej Halla przyczynił się do błędu (ok.20 %) koncentracji oraz ruchliwości nośników. Wykres jak i wyniki z tego ćwiczenia świadczą o tym, iż dzięki zastosowaniu multimetru cyfrowego do pomiaru napięcia Halla dało doskonały rezultat. Charakterystyka jest liniowa tak jak się tego spodziewaliśmy bez wielkich błędów.

---