Wydział A , E i I Kierunek A i R
Ćwiczenie laboratoryjne z fizyki:
Zjawisko Halla
Grupa III sekcja V
Bratek Łukasz
Mazurkiewicz Rafał
Mikołajczyk Radosław
Gliwice 7.03.1997
1 . Wprowadzenie .
Hallotron jest to element półprzewodnikowy , którego działanie oparte jest na zjawisku Halla . Zasadniczą częścią hallotronu jest albo prostopadła płytka ( o powierzchni kilkunastu milimetrów kwadratowych i grubości ok. 0,3 mm) , albo cieńka warstwa półprzewodnika naparowana w próżni na podłożu dielektrycznym . Hallotron ma dwie pary elektrod z których dwie są prądowe , a
dwie napięciowe ( wyjściowe ) . Elementy te są stosowane do pomiarów i regulacji natężenia pola magnetycznego , pomiaru mocy czynnej i biernej , oraz do pomiarów dużych prądów ( ważne jest że pomiar odbywa się bez przerywania obwodu prądowego ) .
Zjawisko Halla związane jest z działaniem siły Lorentza na nośniki ładunku elektrycznego poruszające się w polach elektrycznym i magnetycznym . Prostokątna płytka hallotronu przez którą płynie prąd elektryczny o natężeniu i , jest umieszczona prostopadle do linii sił pola magnetycznego o indukcji B .
Na poruszające się ładunki działa siła Lorentza :
Siła ta jest przyczyną przesunięcia ładunków do jednej z krawędzi płytki i powstania pola elektrycznego o natężeniu E . Odchylenie ładunków następuje do chwili gdy siła Lorentza zostanie zrównoważona siłą elektrostatyczną :
Różnica potencjałów powoduje powstanie napięcia ( zwanego napięciem Halla ) pomiędzy bocznymi ściankami płytki określanego wzorem :
b - szerokość płytki
ponieważ u - ruchliwość nośników prądu
oraz d - długość płytki
n - koncentracja elektronów
po podstawieniu i uproszczeniu otrzymujemy :
stosunek nazywamy stałą Halla .
Widać iż napięcie Halla jest proporcjonalne zarówno do indukcjji magnetycznej jak i do prądu płynącego przez hallotron .
Należy pamiętać iż zjawisku Halla towarzyszy szereg efektów termoelektrycznych i termomagnetycznych mających wpływ na wartość napięcia Halla . Najbardziej istotny wpływ ma tzw. napięcie asymetrii pierwotnej do którego kompensacji stosuje się dołączane do hallotronu potencjometry .
2 . Opis ćwiczenia :
2.1 Układ pomiarowy
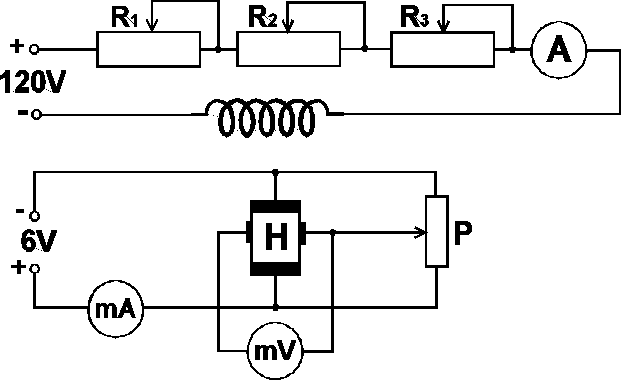
2.2 Przebieg ćwiczenia
Przy trzech różnych wartościach prądu zasilającego elektromagnes Im
( Im = 3 , 5 , 7 A ) wykonano serię pomiarów napięcia Halla UH dla kolejnych wartości natężenia prądu sterującego IS ( wartość prądu I S zmieniamy 0*26 mA co 2 mA) . Przed odczytem wartości napięcia Halla za każdym razem przy wyłączonym obwodzie cewki nastawiano żądaną wartość prądu IS płynącego przez hallotron i kompensowano ją napięciem asymetrii , następnie włączano prostownik i notowano wskazanie miliwoltomierza .
3 . Opracowanie wyników pomiarów :
3.1 Analiza błęów
Dla prądu IM płynącego przez cewkę błąd obliczamy według wzoru:
![]()
Im [A] |
Im [A] |
3 |
0.075 |
5 |
0.105 |
7 |
0.135 |
Dla napięcia Halla błąd obliczamy według wzoru:
![]()
Im=3A |
Im=5A |
Im=7A |
|||
UH |
UH |
UH |
UH |
UH |
UH |
0 |
0.1 |
0 |
0.1 |
0 |
0.1 |
0.9 |
0.1045 |
1.6 |
0.108 |
2.2 |
0.111 |
2.0 |
0.11 |
3.1 |
0.1155 |
4.2 |
0.121 |
2.8 |
0.114 |
4.6 |
0.123 |
6.2 |
0.131 |
3.7 |
0.1185 |
6.0 |
0.13 |
8.3 |
0.1415 |
4.6 |
0.123 |
7.5 |
0.1375 |
10.3 |
0.1515 |
5.7 |
0.1285 |
8.9 |
0.1445 |
12.3 |
0.1615 |
6.3 |
0.1315 |
10.5 |
0.1525 |
14.3 |
0.1715 |
7.2 |
0.136 |
11.8 |
0.159 |
16.3 |
0.1815 |
8.0 |
0.14 |
13.2 |
0.166 |
18.3 |
0.1915 |
8.8 |
0.144 |
14.7 |
0.1735 |
20.0 |
0.2 |
9.6 |
0.148 |
15.8 |
0.179 |
22.0 |
0.21 |
10.5 |
0.1525 |
17.1 |
0.1855 |
24.0 |
0.22 |
11.2 |
0.156 |
19.0 |
0.195 |
26.2 |
0.231 |
Dla prądu IS błąd obliczamy według wzoru:
3 . 2 Metodą regresji liniowej obliczamy współczynnik nachylenia charakterystyk
![]()
ze wzorów
gdzie
oraz jego błąd
3 . 2 . 1 Obliczenia
a) Im = 3 A
a = 0,43
b = 0,21 * 10 -3
a = 9,2 * 10 -3
b) Im = 5 A
a = 0,717
b = 0,23 * 10 -3
a = 11,8 * 10 -3
c) Im = 7 A
a = 0,997
b = 0,22 * 10 -3
a = 9,6 * 10 -3
3 . 3 Wyznaczamy stałą hallotronu :
gdzie :
n=1500 - liczba zwojów l = 0,95 m - długość cewki
![]()
błąd stałęj hallotronu obliczamy za pomocą różniczki zupełnaj z wzoru :
3 . 3 . 1 Obliczenia
a) Im = 3 A
= 72,23
= 3,35
b) Im = 5 A
= 72,27
= 2,7
c) Im = 7 A
= 71,78
= 2,08
3 . 4
Następnie wyznaczamy ze wzoru na średnią ważoną stałą hallotronu
oraz jej błąd
gdzie
3 . 4 . 1 Obliczenia
w1 = 0,089
w2 = 0,137 = 71,99 = 1,479
w3 = 0,231
3 . 5
Obliczamy stałą Halla ze wzoru :
RH = * d = 5,76 * 10 -3 dla d = 0,08 * 10 -3 [ m ] - grubość użytego hallotronu
oraz jej błąd ze wzoru
RH = * d = 0,118 * 10 -3
3 . 6
Liczymy
= 1,10 * 10 21
gdzie e - elektryczny ładunek elementarny = 1,602 * 10 -19 [ C ]
oraz = 0,02 * 10 21
4 . Podsumowanie
Napięcie Halla jest wprost proporcjonalne do pola magnetycznego. Jeżeli będziemy zwiększać pole magnetyczne wzrośnie nam jednocześnie napięcie Halla.Otrzymana stała Halla jest większa od zera, wynika z tego, że dominującym typem przewodnictwa w badanym hallotronie jest typ dziurowy, więc jest to półprzewodnik.
Wyszukiwarka
Podobne podstrony:
algorytmy-mini, POLITECHNIKA wydział E kierunek I, ALGORYTMY I ZLOZONOSC, ROZNE JAKIES TAM
algorytmy, POLITECHNIKA wydział E kierunek I, ALGORYTMY I ZLOZONOSC, ROZNE JAKIES TAM
Procesor 8086, POLITECHNIKA wydział E kierunek I, ARCHITEKTURA SYSTEMOW KOMPUTEROWYCH
Algorytmy i złożoność, POLITECHNIKA wydział E kierunek I, ALGORYTMY I ZLOZONOSC, ROZNE JAKIES TAM
ALgorytmy i programowanie, POLITECHNIKA wydział E kierunek I, ALGORYTMY I ZLOZONOSC, ROZNE JAKIES TA
06 handout2backhouse1, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyc
09 handout2lazear, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyczne,
opcje ii przyklady tresc, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matema
LABORKA1, WspolPrzewodII, Wydzia˙ AEiI, kierunek AiR
LABORKA1, WspolPrzewodII, Wydzia˙ AEiI, kierunek AiR
13 handout2freyh, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyczne,
mikro zadania 4, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyczne, W
opcje ii zadania, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyczne,
mgo-syllabus, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyczne, WNE
forward zadania, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki matematyczne, W
logika przykladowe zadania, Wydział Zarządzania WZ WNE UW SGH PW czyli studia Warszawa kierunki mate
więcej podobnych podstron