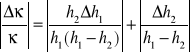Ćwiczenie 18

Wyznaczanie stosunku =c_p/c_v dla powietrza metodą
Clémenta-Desormesa

1. Podstawa teoretyczna i przebieg doświadczenia

Wykładnik adiabaty κ równy jest stosunkowi ciepła właściwego gazu przy ogrzewaniu go pod stałym ciśnieniem (c_p) do ciepła właściwego tego gazu przy ogrzewaniu go przy stałej objętości (c_v). Ponieważ podczas ogrzewania przy stałym ciśnieniu gaz zwiększa swą objętość, a zatem wykonuje pracę, c_p jest zawsze większe od c_v, a więc κ=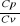
będzie zawsze większe od 1.

Dla dowolnego gazu wartość κ jest stała - zależy ona wyłącznie od budowy cząsteczek gazu. Dla gazów, których cząsteczki są dwuatomowe, a z takich w 99% składa się powietrze, κ==1,4.

Powyższy wynik otrzymujemy łącząc dwa wzory. Ciepło molowe gazu w stałej objętości określa wzór

1. 
   ,

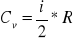
gdzie i oznacza liczbę stopni swobody drobin gazu, czyli liczbę niezależnych parametrów określających stan drobiny, R=8,31 J*mol^-1*K^-1 - stała gazowa.

Ciepło molowe gazu (równanie Mayera):

2. 
   

Ze wzorów (1) i (2) mamy:

3. 
   ,

a dla powietrza i= 5.

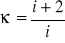
Doświadczalny pomiar wartości κ przeprowadzimy następująco:

1. 
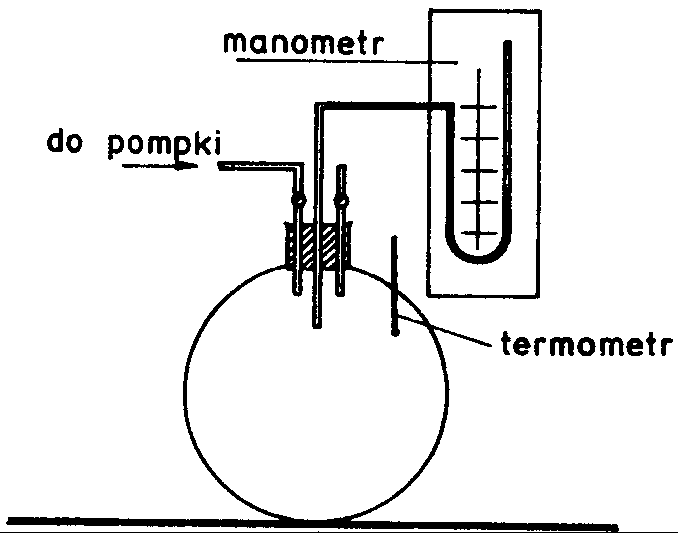
   W butli szklanej o dużej pojemności sprężamy powietrze do ciśnienia p + p₁, gdzie p oznacza ciśnienie atmosferyczne. Po wyrównaniu się temperatury gazu w butli (należy odczekać kilka minut), odczytujemy różnicę wysokości słupa cieczy na manometrze, która jest proporcjonalna do nadwyżki ciśnienia p₁.

2. Spuszczamy powietrze z butli przez otwarcie kurka, po czym kurek zakręcamy. Biorąc pod uwagę krótki czas potrzebny na zejście powietrza z butli, możemy założyć, że zaszła przemiana adiabatyczna.

3. Czekamy na wyrównanie się temperatury w butli z temperaturą otoczenia i odczytujemy różnicę wysokości słupa cieczy na manometrze, która jest proporcjonalna do nadwyżki ciśnienia p₂.

Stan końcowy jest stanem po przemianach adiabatycznej oraz izochorycznej. Ten sam stan można osiągnąć drogą bezpośredniej przemiany izotermicznej, tak więc:

Wyznaczając z równania drugiego:

(5)

i podstawiając do pierwszego, dostajemy:

(6)

Przekształcając i rozwijając obie strony w szereg Maclaurina, przy założeniu p₁«p oraz p₂«p, otrzymujemy:

(7) κ=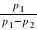

Ponieważ wysokość słupa cieczy w manometrze określona jest przez p_x=ρgh_x, a więc jest wprost proporcjonalna do ciśnienia, można napisać:

(8) κ=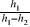

Przeprowadzono dwanaście pomiarów różnic wysokości słupa cieczy h₁ i h₂.

2. Metody obliczania błędów pomiaru

Przy pomiarach h₁ oraz h₂, odczyty z manometru miały niepewność 1mm (taka była najmniejsza podziałka, a nie dało się odczytywać połówek). Ponieważ zarówno h₁ jak i h₂ były różnicami dwóch pomiarów, ich niepewności bezwzględne dodają się, a więc Δh₁=Δh₂=2mm (oznaczmy tę niepewność przez Δh)

Δκ obliczono ze wzoru:

9. Δκ_i=κ_i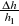
   

Błąd pojedynczego pomiaru stosunku  obliczamy metodą różniczki zupełnej:

(10)

3. Wyniki i obliczenia

pomiar	h1 [mm]	h2 [mm]	κ	Δκ
1	65	20	1,44	0,044	0,058
2	69	17	1,33	0,038	0,048
3	66	18	1,38	0,042	0,053
4	71	18	1,34	0,038	0,047
5	64	18	1,39	0,043	0,056
6	68	17	1,33	0,039	0,049
7	62	17	1,38	0,044	0,057
8	66	18	1,38	0,042	0,053
9	63	17	1,37	0,043	0,055
10	66	19	1,40	0,043	0,055
11	65	17	1,35	0,042	0,053
12	68	19	1,39	0,041	0,052
Wartości średnie:			1,37	0,042	0,053

4. Analiza błędów

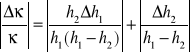
Jak wspomniano przy metodach obliczania błędów niedokładność odczytów manometru wynosi h=2mm. Jeśli spojrzeć zwłaszcza na pomiar różnicy słupów cieczy po przemianie adiabatycznej, błąd ten należy uznać za dość duży.

Pośród otrzymanych obliczeń wykładników adiabaty  tylko jeden wynik okazał się większy od wartości średniej równej 1,4. Przyczyną tego może być nieszczelność układu doświadczalnego, co powodowało uchodzenie powietrza z butli, a tym samym wyrównywania się ciśnienia w niej panującego z atmosferycznym. Mamy zatem do czynienia z błędem systematycznym, którego innym przykładem może być zmienna insolacja stanowiska doświadczalnego.

Pomimo to uzyskane wyniki nie odbiegają o więcej niż 6% od teoretycznej wielkości.

5. Wnioski

Dość precyzyjne wyniki, mimo wskazanej przed chwilą znacznej niedoskonałości pomiarów, pozwalają wysnuć wnioski, że pomiar stosunku ciepła właściwego przy przemianie izobarycznej do ciepła właściwego dla stałej objętości nie jest czuły na te rodzaje błędów. Tak więc w wielu przypadkach otrzymane rezultaty będą zadowalające.

Doświadczenie pokazuje, że od jednego do drugiego stanu gazu można przejść na więcej niż jeden sposób.

Najważniejszy wniosek płynie z faktu, że >1, co oznacza, że ciepło molowe gazu pod stałym ciśnieniem jest większe od ciepła molowego gazu w stałej objętości.

1

2

---