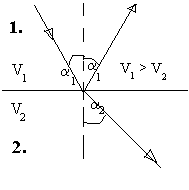
1.Promień odbity , padający i załamany oraz normalna do powierzchni granicznej leżą w jednej płaszczyźnie.
DEFINICJE
Prawa odbicia i załamania światła.

1.Promień odbity , padający i załamany oraz normalna do powierzchni granicznej leżą w jednej płaszczyźnie.
2.Kąt padania α1 jest równy kątowi odbicia α1': α1=α1'
3.Stosunek sinusa kąta padania α1 do sinusa kąta załamania α2 jest wielkością stałą i wynosi: sinα1/sinα2=n2,1, gdzie n jest współczynnikiem załamania światła ośrodka 2, do którego wchodzi promień, względem ośrodka pierwszego z którego wychodzi.
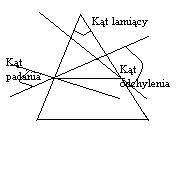
Pryzmat optyczny-ośrodek załamujący światło, ograniczony dwiema płaszczyznami, tworzącymi ze sobą kąt łamiący ϕ. Kierunek promienia świetlnego wychodzącego z pryzmatu jest odchylony od promienia padającego o pewien kąt δ, zwany kątem odchylenia. Wartość tego kąta zależy od kąta padania α, kąta łamiącego ϕ i współczynnika załamania n pryzmatu. Kąt odchylenia osiąga minimum, gdy wewnątrz pryzmatu promień jest prostopadły do dwusiecznej kąta łamiącego. W tym przypadku kąt δ=δmin, stanowi sumę kątów nie przyległych w trójkącie ABC, czyliδ=2(α-β). Ponieważ kąty β i ϕ/2 mają ramiona wzajemnie prostopadłe, zachodzi równośćβ=ϕ/2, która po podstawieniu do wyrażenia na δpozwala wyrazić kąt α poprzez δ i ϕ:α=(δ+ϕ)/2. Podstawiając te zależności do wzoru na współczynnik załamania światła otrzymujemy:
n=sin[(δ+ϕ)/2]/sin[ϕ/2]
Współczynnik załamania światła. Jeśli kąt padania światła w ośrodku I wynosi α, a kąt załamania w ośrodku II wynosi β, to współczynnik załamania ośrodka II względem ośrodka I jest równy: n=sinα/sinβ=VI/VII, gdzie VI i V2 oznaczają prędkości w ośrodkach I i II. Według tablic fizycznych współczynniki załamania światła dla różnych rodzajów szkła wynoszą odpowiednio:
Szkło crown lekkie-1,515
Szkło crown ciężkie-1,615
Szkło flint lekkie-1,608
Szkło flint ciężkie-1,754
Szkło kwarcowe-1,459
Spektrometr- jest przyrządem umożliwiającym dokładny pomiar kąta odchylenia promienia przez pryzmat.
CEL ĆWICZENIA
Wyznaczenie współczynnika załamania szkła, z którego wykonany jest pryzmat, przy pomocy spektrometru, korzystając z wyliczonych przy pomocy niego kątów łamiącego i najmniejszego odchylenia. Współczynnik załamania szkła powinien osiągnąć wartości zbliżone do tych odczytanych przeze mnie z tablic fizycznych(1,515-1,754). Jeżeli jego wymiar będzie bardzo odbiegał od tych wielkości, będzie to oznaczało, że doświadczenie zostało wykonane błędnie. Ćwiczenie to składa się z dwóch części:
1.Wyznaczenie kąta łamiącego pryzmatu.
2. Wyznaczenie kąta najmniejszego odchylenia.
WYKONANIE ĆWICZENIA
1.Wyznaczenie kąta łamiącego pryzmatu- ϕ.
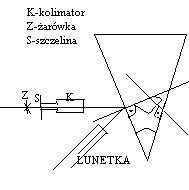
*Szczelinę S oświetlamy źródłem światła białego(Z-żarówką).
*Stawiamy pryzmat na stoliku i sprawdzamy czy obraz jest symetryczny względem średnicy poziomej.
*Stolik obracamy do pozycji, przy której obraz szczeliny znajduje się na środku krzyża z nitek pajęczych.
*Notujemy wskazania noniuszy A i B. Odczytane wartości opisują położenie pierwszej ściany.
*Obracamy stolik w celu uzyskania w lunetce odbicia od drugiej ściany kąta łamiącego pryzmatu. Notujemy wskazania noniuszy A i B.
*Znajdujemy różnicę położeń Ψ pierwszej i drugiej ściany.
*Znajdujemy kąt łamiący ϕ.ϕ=|180°-Ψ|
*Kąt łamiący wyznaczamy trzykrotnie, zmieniając za każdym razem położenie pryzmatu na stoliku.
* Obliczamy wartość kąta łamiącego, który jest średnią wszystkich wartości ϕ obliczonych w sześciu próbach.
Wyniki pomiarów przedstawia tabelka.
Położenie I ściany |
Położenie II ściany |
Różnica położeń-Ψ |
ϕ=|180°-Ψ| |
Kąt najmniejszego odchylenia |
||||
A |
B |
A |
B |
A |
B |
A |
B |
ϕ=ϕśr |
341°20' |
161°2' |
221°20' |
41°21' |
120°00' |
119°59' |
60°00' |
61°01' |
59°10'
|
315°20' |
140°25' |
195°15' |
15°20' |
120°05' |
125°05' |
59°55' |
54°55' |
|
210°30' |
40°20' |
332°20' |
160°20' |
122°10' |
120°00' |
58°10' |
60°00' |
|
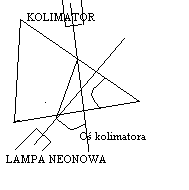
2.Wyznaczanie kąta najmniejszego odchylenia δ
*Przed szczeliną kolimatora ustawiamy lampę neonową.
*Patrząc w okular lunetki obracamy ją wokół stolika i szukamy rozszczepionego, barwnego obrazu szczeliny. Zwężamy szczelinę tak, aby jej obraz składał się z wyraźnie rozdzielonych wąskich prążków.
*Obracamy nieco stolik w jedną i w drugą stronę i obserwujemy kierunek przesuwania się obrazu szczeliny- wybieramy kierunek obrotu, przy którym odchylenie promieni załamanych zmniejsza się. Ustalamy położenie stolika dokładnie w punkcie zwrotnym (jak na rysunku)- kąt odchylenia osiąga wówczas minimum.
Gdy stolik znajduje się w punkcie zwrotnym, ustawiamy lunetkę tak, aby krzyż z nici znalazł się dokładnie w żółtym prążku widma neonu.
Notujemy w tabeli położenia αi obu noniuszy, odpowiadające minimum odchylenia.
Nie poruszając stolika i obracamy lunetkę do pozycji na wprost kolimatora - ustawiamy ją tak, aby obraz szczeliny znalazł się na środku krzyża. Notujemy wskazania ci obu noniuszy - odpowiadają one położeniu lunetki dla promienia nie odchylonego.
Obliczamy kąt minimalnego odchylenia δi - jest on równy różnicy położeń lunetki dla promienia odchylonego: δi=│αi - ci│
Pomiar kąta najmniejszego odchylenia δ powtarzamy trzykrotnie.
Obliczamy wartość kąta najmniejszego odchylenia δ, który jest średnią pomiarów różnicy położeń.
Pomiary dokonane za pomocą spektrometru przedstawia tabela:
POŁOŻENIE LUNETY |
RÓŻNICA POŁÓŻEŃ |
Kąt najmniejszego odchylenia |
||||
Przy najmniejszym odchyleniu-α |
Na wprost kolimatora-c |
δ=|α-c| |
δ=δśr |
|||
106°50' |
286°50' |
60°00' |
241°00' |
45°50' |
45°00' |
45°40' |
104°20' |
284°30' |
62°30' |
240°50' |
43°20' |
43°40' |
|
110°10' |
287°30' |
62°50' |
240°50' |
47°20' |
47°10' |
|
Mogę teraz, korzystając ze wzoru n=sin[(δ+ϕ)/2]/sin[ϕ/2] obliczyć współczynnik załamania szkła(dla żółtej linii neonu).Wynosi on n=1,61
WNIOSEK. Otrzymana przeze mnie w wyniku doświadczenia wartość mieści się w granicach podanych w tablicach fizycznych, co pozwala mi sądzić, że doświadczenie zostało wykonane prawidłowo. Nie oznacza to jednak, że otrzymany przeze mnie wynik nie jest obarczony błędami pomiarowymi.
RACHUNEK BŁĘDÓW
Wielkościami obarczonymi błędami są wartości kątów δ i ϕ oraz sam współczynnik załamania szkła-n.
^Błąd pomiaru Δϕ jest błędem maksymalnym. Obliczam go jako maksymalną wartość różnicy pomiędzy wartością średnią ϕśr a każdą z wartości ϕ.Δϕ=max|ϕśr-ϕ|. Błąd Δϕ=4°15'=0,074rad
^Błąd pomiaru Δδ także jest błędem maksymalnym. Obliczam go jako maksymalną wartość różnicy pomiędzy wartością δśr a różnicami położeń δ.Δδ=max|δśr-δ|. Błąd Δδ=1°40'=0,029rad
^Błąd Δn jest błędem pomiaru, który obliczam ze wzoru
Δn=sin[δ/2]*Δϕ /2sin2[ϕ/2]+cos[(ϕ+δ)/2]*Δδ /2 sin[ϕ/2] Błąd ten wynosi: Δn=0,094
^Doświadczenie wymaga również obliczenia błędu względnego procentowego. Obliczamy go ze wzoru: Bp=(Δn/n)*100% Względny błąd procentowy dla wykonanego doświadczenia wynosi Bp= 5,87%
WNIOSKI
Błąd procentowy nie jest zbyt duży więc nie ma wielkiego wpływu na wynik. Mógł on być jednak spowodowany: -niedokładnym odczytem z noniuszy A i B,
-niedokładnym ustawieniem spektrometru i nieodpowiednim ustawieniem na nim pryzmatu.
NATALIA WALCZAK WYDZ. INŻ. PROD.
ZIP DZIEŃ TYGODNIA- PONIEDZIAŁEK
GR.7 GODZINA: 14-17
ĆWICZNIE 13
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA