1. Układ sterowania powinien zapewnić sterowanemu obiektowi takie warunki, w których przebieg wielkości sterowanej ('wyjście' obiektu, zmienna procesowa) w jakimś sensie odtwarza przebieg wielkości zadanej, czemu na przeszkodzie stoi przede wszystkim dynamika ('inercja') obiektu sterowania oraz obecność zakłóceń. Wielkość zadana podawana jest na zadajnik, którego zadaniem jest: a) kształtowanie żądanej relacji między wielkością zadaną, a wielkością sterowaną¡, b) dostarczanie sygnału odniesienia dla sygnałów pozyskiwanych z czujników wielkości sterowanej (ograniczenie sygnału, filtracja, prekompensacja, dostarczenie sygnału różnicowego). Sterownik ma za zadanie: a) zapewnienie układowi zamkniętemu stabilności, b) kształtowanie żądanej relacji między wielkością zadaną, a wielkością sterowaną, c) ograniczanie wpływu ('usuwanie') zakłóceń d) ograniczanie wpływu niepewności wiedzy o sterowanym obiekcie ('uniewrażliwienie' sterowanej zmiennej na błędy modelowania, ograniczenia wynikające z nieliniowości, niestacjonarność charakterystyk sterowanego obiektu, itp). Czujnik w torze sprzężenia zwrotnego dostarcza informacji o efektywności procesu sterowania.

Sprzężenie zwrotne w układach sterowania: a) zmniejszenie wpływu zakłóceń na wielkość sterowaną b) zmniejszenie wpływu niestacjonarności, niepewności oraz nieliniowości charakterystyk elementów układu sterowania, c) modyfikacja statycznych oraz dynamicznych charakterystyk obiektu (przede wszystkim stabilizacja układu zamkniętego) d) umożliwienie realizacji zadania nadążania, e) umożliwienie rekonstrukcji pomiarowo niedostępnych zmiennych procesowych (koncepcja tak zwanych obserwatorów zmiennych stanu).

e) groźba utraty stabilności układu zamkniętego, f) 'przenoszenie' zakłóceń w torze pomiarowym 'na obiekt'.

2. Zadanie przestawiania a) rzadkie, ale gwałtowne zmiany sygnału zadającego, b) duży (istotny) wpływ zakłóceń, c) mały uchyb e(t) możliwy tylko dla chwil czasu wystarczająco odległych od momentu zmiany sygnału zadającego.
, e_max—dopuszczalny uchyb, ts-czas ustalania t>=T_s Np. sterowanie windą

Zadanie nadążania a) ciągłe zmiany o niegwałtownym charakterze; b) wpływ zakłóceń we wstępnych procesach projektowania do
pominięcia; c) mały uchyb e(t) dla każdej chwili sterow.

3. Nie można np. uzyskać dużej dokładności sterowania i krótkiego czasu wykonania. Ramię robota może szybko i z dużym przeregulowaniem (czyli ryzykując zniszczenie przedmiotu) dosunąć go do ściany, albo dokładnie, lecz powoli przesunąć go bez takiej groźby.

4. Model wejściowo-wyjściowy

G(s) - transmitancja (f. przenoszenia) układu dynamicznego --> Y(s)=U(s)*G(s)

y(t) = u(t)*g(t) =granice całki[0,t]  u(t)g(t- )du(t-)g(t)d <= splot

U(s) i Y(s) mogą być wektorami, więc G(s) to w ogólności macierz operatorowych transmitancji. G(t)G(s): G(s)=L[g(t)] ; g(t)=L^-1[G(s)]

Para wielkości związana prostym i odwrotnym przekształc. Laplace'a

Model w przestrzeni stanu:

X(t)=Ax(t)+B(t) równanie stanu, relacja dynamiczna

Y(t)=Cx(t)+D(t) równanie wyjścia, relacja statyczna

X(t)- wektor stanu u(t)- wektor pobudzeń, y(t)- wektor wyjść (obserw)

Zmienne stanu: zbiór o minimalnej liczności takich wielkości, których znajomośc w chwili to (wraz z informacją o przyszłym sterowaniu u(t)) jednoznacznie określa zachowanie się układu w przyszłości.

Zwiazek miedzy tymi modelami:

L[x(t)]=L[Ax(t)+Bu(t)]

SX(s)-x(0)|_x(0)=0=AX(s)+BU(s)

SX(s)=AX(s)+BU(s)  (s)=(sI_m-A)^-1

(SI_m-A)X(s)=BU(s)  (t)=L^-1[[(sI_m-A)^-1]=e^At

X(s)=(sI_n-A)^-1BU(s) macierz fundamentalna

L[y(t)]=L[Cx(t)+Du(t)]

Y(s)=CX(s)+DU(s)

Y(s)=[C(SI_m-A)^-1 B+D]U(s)

G(s)=C(SI_m-A)^-1B+D=C(s)B+D <=operatorowa transmitancja

5. Dane są dwa n - wymiarowe modele w przestrzeni stanu:

x'(t) = A_xx(t) + B_xu_x(t) , x(0).

y_x(t) = C_xx(t) + D_xu_x(t)

z'(t) = A_zz(t) + B_zu_z(t) , z(0)

y_z(t) = C_zz(t) + D_zu_z(t)

Modele te nazywamy parametrycznie podobnymi, jeżeli istnieje taka macierz P∈R^{n x m} (nieosobliwa macierz podobieństwa), że:

A_z = P^-1A_xP B_z = P^-1B_x C_z = C_xP D_z = D_x

Modele te nazywamy podobnymi o ile są parametrycznie podobne a ponadto: u_x(t) = u_z(t) = u(t) oraz x(0) = Pz(0)

Modele parametrycznie podobne mają taką samą operatorową transmitancję, a więc i odpowiedzi impulsowe i skokowe: G_x(s)=G_z(s)

Dla modeli podobnych ponadto: x(t) = P*z(t) y_x(t) = y_z(t) = y(t)

6. Rozwiązanie tego równania ma postać:

x(t) = e^Atx(t₀) , gdzie e^At - macierz fundamentalna

jest ona definiowana przez analogię:

Φ(s) = (sI_n - A)^-1 - postać operatorowa mac. fundamentalnej

£^-1[1/s-α] = e^αt £^-1[1/sI_n-A] = e^At e^At = def.=

Macierz modalną można wyznaczyć poprzez diagonalizację

M = [x₁ ; x₂ ;…;x_n] , M∈R^{n x m} - macierz modalna zawierająca wektory własne x_i, i∈{1,…,n} macierzy A.

M^-1 =
,y_i∈Cⁿ i∈{1,2, ,n} Λ=

Λ∈R^{n x m} - macierz diagonalna zawiera wartości własne λ_i macierzy A e^Λt =
, e^At = M e^Λt M^-1 lub e^At =

9. diagonalizacja - wyznaczenie takiej macierzy Λ o strukturze macierzy diagonalnej, która pozostaje w relacji podobieństwa z pierwotną macierzą A, a macierzą podobieństwa jest mac. modalna M.

a) Wyznaczanie zbioru wartości własnych macierzy A (λ₁λ₂,..,λ_n)

det -(A -λ_iI_n) = 0 - r - nie charakterystyczne

b) Wyznaczanie przykładowych wektorów własnych odpowiadających uzyskanym wartościom własnym oraz zapisanie ich w tzw. Macierzy modalnej M: (A -λ_iI_n)x_i = 0 , i= 1,2,..,n , M = [x₁ x₂..x_n] , M∈R^{n x m}

c) Wyznaczanie macierzy diagonalnej wg wzoru:

Λ=M^-1A*M , Λ∈R^{n x m} Λ= diag {λ_i} i=1,2…n

10. Ukł. Jest BIBO stabilny (reprezentowany przez g(t) lub G(s)) , jeżeli: 1) u(wej) є L_∞ => y(wyj) є L_∞ ; 2) ||y||_∞≤ c||u||_∞ dla pewnej stałej c≥0 oraz dla każdego u є L_∞. Czyli ukł. jest BIBO stabilny jeżeli jeżeli każdemu ograniczonemu wejściu odpowiada ograniczone wyjście. Kryterium: wszystkie bieguny transmitancji G(s) muszą być w lewej otwartej półpłaszczyźnie zespolonej.

11. Ukł. x'(t)=Ax(t) jest asymptotycznie stabilny<=>gdy dla dowolnych warunków początkowych x(0) є Rⁿ zachodzi lim_t->∞||x(t)||= 0. Asyst. stab. definiuje się tylko dla ukł. o zerowym pobudzeniu u(t)=0. Kryterium AS: wszystkie wartości własne macierzy A muszą leżeć w lewej otwartej półpłaszczyźnie płaszcz. zespolonej.

12. Układ jest wewnętrznie stabilny <=>gdy jest BIBO stabilny dla każdej pary wejście wyjście możliwej do wyróżnienia w tym układzie. Kryterium: a) wyznacznik 1+G_p(s)G_c(s)G_s(s)=0 nie posiada zer w prawej domkniętej półpłaszczyźnie płaszczyzny zespolonej; b) w iloczynie G_p(s)G_c(s)G_s(s) nie występują skreślenia parach złożonych z zera i bieguna z prawej półpłaszczyzny płaszcz zespolonej.

14. Uchyb - różnica pomiędzy zadaną wartością a wielkością sterowaną e(t) = r(t)-c(t). Pewne informacje o uchybie niesie sygnał różnicowy przetwarzany przez sterownik. Uchyb pojawia się na skutek działania zakłóceń: a) na wejściu obiektu sterowanego; b) pomiarowych;. Uchyb można ograniczyć zwiększając wartość wzmocnienia w torze głównym, ale w taki sposób, aby ukł nie stracił stabilności. Zachodzi bowiem
; k_p=lim_s->∞ G_p(s)G_c(s); k_v=lim_s->∞ sG_p(s)G_c(s); k_a=lim_s->∞ s²G_p(s)G_c(s). Albo stosując człon całkuj. przed węzłem, do którego wchodzą zakłócenia.

15.







Stabilny ukł. regulacji automatycznej charakteryzuje się astat I rzędu, jeżeli posiada skończone i niezerowe wzmocnienie prędkościowe k_v ≠0; k_v ≠∞; k_v=lim_s->∞ sG_p(s)G_c(s); Czyli wartość uchybu sygnałowego w stanie ustalonym przy pobudzeniu skokiem jednostkowym jest równe zero.

G(s)=s/s-k jest G(s)=s+k(m-1)/s+mk nie jest

16. Stosując podany korektor układ zamknięty straci wewnętrzną stabilność. Istnieje, bowiem zasada, że korektor nie może eliminować niestabilnych biegunów obiektu (leżących w prawej domkniętej półpłaszczyźnie płaszczyzny zespolonej).

17. Dany jest model:

, dla jednostkowego sprzężenia zwrotnego i przy braku zadajnika możemy zapisać:

⇒ k=2 i T>0 ⇒ e_{_↑}(∞)= lim _s⇒0 s*G_re(s)*(1/s²)=0

18. 1) Linie pierwsiastkowe zaczynają się w biegunach i kończą w zerach układu otwartego.

2) Jeżeli zer jest mniej niż biegunów, to część LP zmierza po asymptotach do ∞.

3) Asymptoty (jeżeli istnieją) przecinają oś rzeczywistą w punkcie σ_a=1/(n-r)*(Σp_i-Σz_i), a kierunki kątowe asymptot liczymy ze wzoru Ψ_a=1/(n-r)*(2m+1)*Π, m=0,1,2,...; n-liczba biegunów układu otwartego;

r-liczba zer układu otwartego; p_i-bieguny; z_i-zera;

4) Asymptoty tworzą symetryczną gwiazdę.

5) LP pokrywają się z osią rzeczywistą tam, gdzie na prawo od danego punktu liczba osobliwości jest nieparzysta.

6) LP spotykają się, załamują i rozchodzą w tzw. Punktach załamania będących rozwiązaniami rzeczywistymi równania: dk/ds=0.

7) Punkty, w których LP przecinają oś jω wyznaczamy: 1+kG₀(s)|_s=jω=0

19. (i) gdy 1+k[L(s)/M(s)] (inaczej - 1+kG₀) - pierwiastki M(s)+kL(s)

Jeżeli k=0 to otrzymamy M(s)=0 --> LP zaczynają się w biegunach G₀ Jeżeli k→nieskończ. to M(s)+kL(s)=0 L(s)=-[M(s)/k] lim(k→nieskończ.)[-M(s)/k]=L(s) zatem LP kończą się w zerach.

21. Aby układ sterowania był dobrze określony, muszą istnieć wszystkie

transmitancje operatorowe zdefiniowane dla trójki zewnętrznych sygnałów {R(s);D(s);N(s)} oraz trójki wyróżnionych wewnętrznych sygnałów {Y1(s); Y2(s); Y3(s)} tego układu. Warunek dobrej określoności sformułować można, zatem w postaci wymagania, aby wyznacznik macierzy występującej we

<< wzorze

nie był tożsamościowo równy zeru >> 1+Gp(s)Gc(s)Gs(s) ≠ 0.

Konieczny i wystarczający warunek dobrej określoności:

Układ jest dobrze określony, (czyli realizowalny), jeżeli wyznacznik 1+Gp(s)Gc(s)Gs(s) nie jest ściśle właściwą, wymierną funkcją zmiennej zespolonej s. Czyli

Przykład: 1+GpGcGs=13/[(s+3)(s+1)]

(s+2)/(s+3) -(s-2)/(s+2)

- (s+5)/(s+1)

22. Do wskaźników bezpośrednich (w dziedzinie czasu) zaliczamy te wskaźniki, które są bezpośrednią miarą określonej cechy przebiegu uchybu e(t) wywołanego standardowym wymuszeniem (np. skokiem jednostkowym). Są to: a) odpowiedź skokowa h(t), b) odpowiedź impulsowa g(t), c) czas ustalania TsΔ, d) czas wystąpienia maksimum przeregulowania T_H, e) tłumienie ξ. Do wskaźników pośrednich (w dziedzinie częstotliwości) zaliczamy te wskaźniki, które na podstawie przebiegu charakterystyk częstotliwościowych pozwalają w przybliżeniu ocenić kształt e(t) przy określonym wymuszeniu. Są to: a) pulsacja drgań tłumionych w₀, b) pulsacja drgań nietłumionych w_n, c) pulsacja rezonansowa w_r, d) 3dB pasmo przenoszenia w_3dB, e) zapas wzmocnienia Mg, Δg, f) zapas fazy Mp , Δp.

Wskaźnik jakości powinien być tak zdefiniowany, aby mierzył żądane cechy przebiegu przejściowego e(t) z dostateczną dokładnością. Nie może nim być sam uchyb e(t), ponieważ jest on funkcją czasu.

23. Znormalizowana odpowiedź skokowa członu inercyjnego:

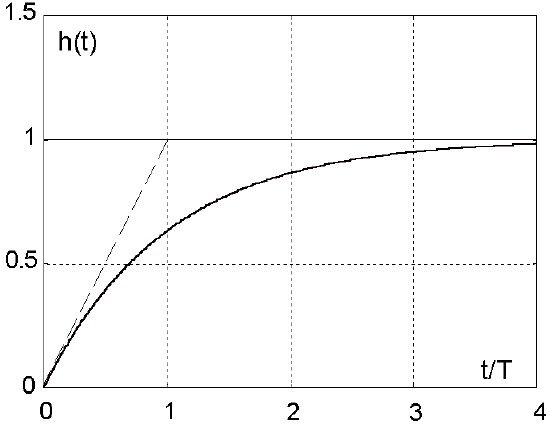
- odpowiedzi impuls. i skok.:

Czas ustalania TsΔ odp. skok.:

TsΔ = {t: h(t)=k(1-Δ)}, 0<Δ<1

TsΔ = -T lnΔ

Charakterystyka widmowa:

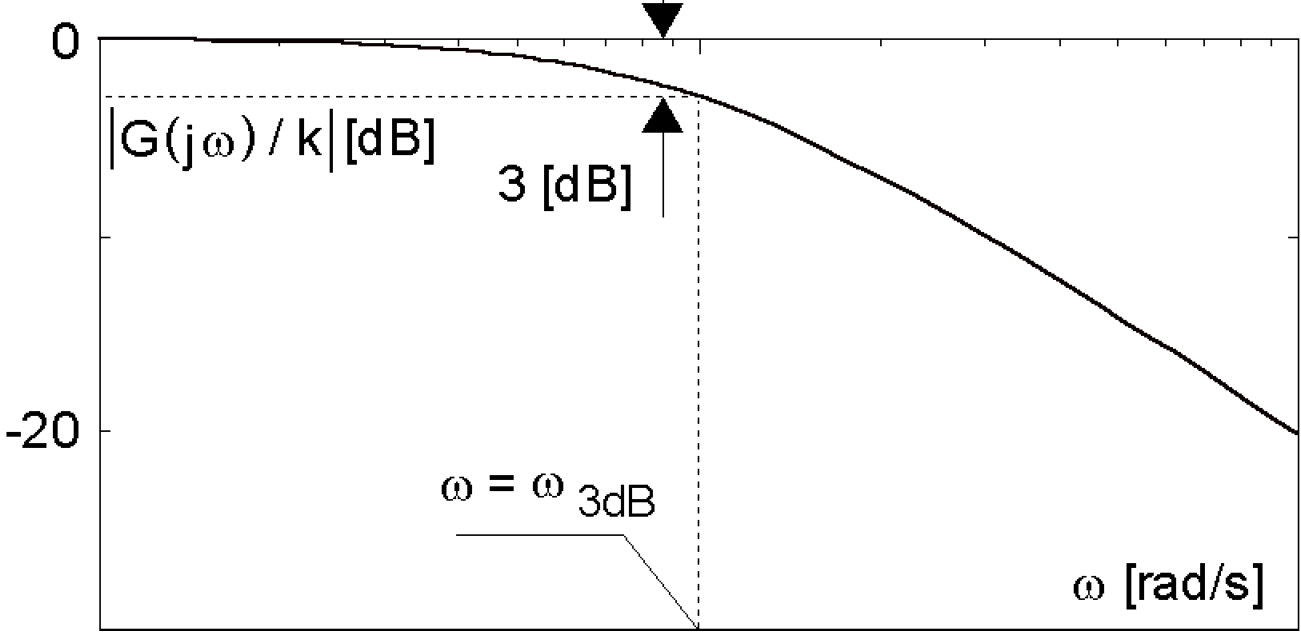
Pulsacja 3dB pasma: w_3dB = 1/T >> M(w3dB)=k/√2 i φ(w3dB)= -45˚

Znormalizowane częstotliwościowe charakterystyki członu inercyjnego:

24. Definicja wskaźników (odp. imp i skok.) dla członu oscylacyjnego

Znormalizowane częstotl. charakterystyki członu oscylacyjnego

Przeregulowanie:
, gdzie:

Czas maksimum:
. Czas ustalania dla strefy kontrolnej 2Δ:
.

Wskaźniki charakterystyki amplitudowej:

-wskaźnik oscylacyjności: Mr=Mmax/M(0) gdzie Mmax=supM(w), w>=0

-pulsacja rezonansowa wr={w: M(w)=Mmax}

-3dB pasmo przenoszenia w_3dB= {w: M(w3dB)=M(0)/√2}

25. Rozważmy prosty układ zamknięty:

- znamy Gp(s)

-szukamy Gc(s)

Transmitancja układu zamkniętego wynosi:

Porównujemy ją z transmitancją wzorcową:

, następnie obliczamy odpowiednie współczynniki: κ, ξ, τ, a z nich odpowiednie wskaźniki (przyjmujemy wcześniej założenia). Zaprojektowany sterownik musi całkowicie skompensować dynamiczne działanie sterowanego obiektu.

26. Po obliczeniach:

,
,

,

dla odpowiedzi skokowej im większe k tym mniejsze tłumienie i krótszy czas ustalania, dla modułu układu:

27. Przeregulowanie
oraz czas maksimum
zależą w następujący sposób od parametrów
, 0<
<1, oraz od
transmitancji:
oraz
Czas ustalania
jest nieciągłą funkcją współczynnika tłumienia
, dla której można podać następującą funkcje majoryzującą

Dla
=0.02 i
oraz przy dostatecznie małych wartościach
mamy:
oraz
.

Wskaźniki
,
oraz
, opisujące amplitudową charakterystykę
członu dynamicznego, związane są parametrami
oraz
tego członu następującymi formułami:

,
, 0<
<
,

Z powyższych wzorów wynika, iż,

28. Zakłada się, że o dynamicznych właściwościach zamkniętego układu decyduje para sprzężonych biegunów jego transmitancji położonych na płaszczyźnie zespolonej w obszarze określonym wymaganiami projektowymi, dotyczącymi przede wszystkim stabilności oraz szybkości procesów przejściowych: s*=-a*+jB*= -ξ/τ +j [sqrt(1-ξ²)]/τ

Obszar definiuje się jako wspólną część półpłaszczyzny leżącej na lewo od s=σ₀, gdzie: σ₀=

oraz stożka wyznaczon kątami

gdzie ^^^

30. Zera funkcji przenoszenia są szkodliwe ze względu na dokładność. Jak wiemy linie pierwiastkowe biegną od biegunów do zer. W związku z tym musimy ograniczać wzmocnienie aby układ był stabilny.

Zera w prawej półpłaszczyźnie nie pozwalają na stosowanie dużych wzmocnień. Skoro jest ograniczenie nastawu wzmocnienia nie możemy zminimalizować uchybu.

31. G=(GcGp)/(1+GcGp) LEAD: Gc(s)=(ao+(a1*)s)/(1+(b1*)s) Wymagania: stabilność, szybkość => s*=-α*+-jβ ; s*=|s*|ejφ* a1(a0)=[a0|Gp(s*)|sin(φ*-v)+sinφ*]/[|s*|G(s*)sinv]

b1(b0)=[-a0|Gp(s*)|sinφ*-sin(φ*+v)]/|s*|sinv] v- kat fazowy obiektu

warunek stabilności regulatora:G1(a0)>0, a0<a0max=[-sin(φ*+v)]/[Gp(s*)|sinφ*] ;stosowalność LEAD: v€ (-360°,-180°)

G=k[s+z]/[s+p]; |z|<|p| Stosując dynamiczny sterownik przyspieszający fazą musimy wszelako liczyć się z koniecznością zapewnienia większych sygnałów sterujących. (stosowne wykresy)

32. LAG: Glag=k{-z+s]/[-p+s] (rys.) Wymagania: szybkość, stabilność=> [-z+s]/[-p+s]przy(s=s*)=∼1 dokładność [-z+s]/[-p+s]przy(s=0)=∼(z/s)→∞

G=s+z/s+p Sterownik opóźniający fazę (LAG) pozwala na zmiejszenie ustalonego błędu prędkościowego. Odbywa się to kosztem: -obnizania szybkości procesów przejściowych w fazie bliskiej stanowi ustalonemu zjawisku tzw. ` przeciąganiu' dotyczy to zwłaszcza odpowiedzi prędkościowej układu zamkniętego. -wzrostu wartości przeregulowaniu skokowej odpowiedzi układu zamkniętego( układu o astatyzmie pierwszego stopnia).

34. Człon inercyjny:

s = ωj
=

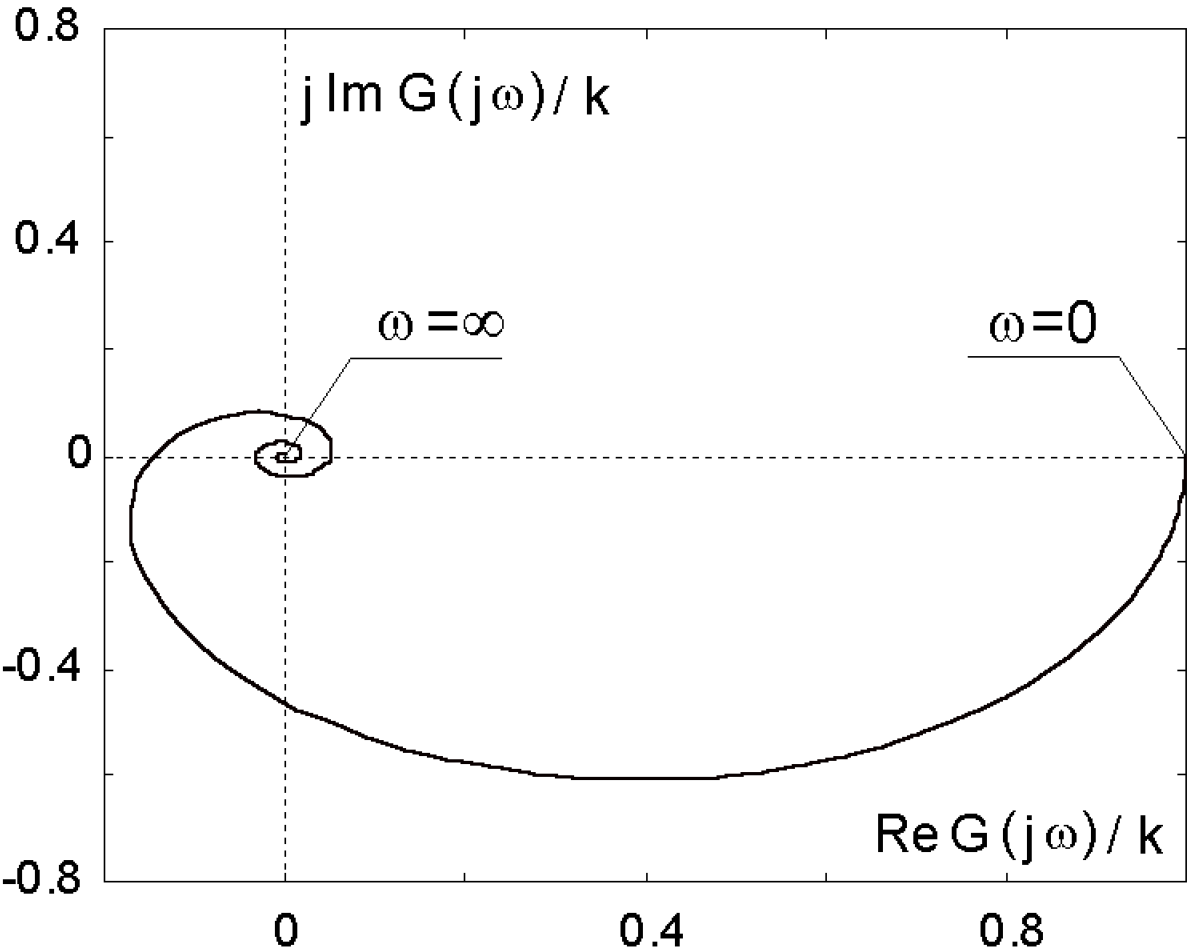
Nyquist: G(jω)=P(ω)+jQ(ω)

Body: G(jω) = |G(jω)| * exp[jφ(ω)] =|G(jω)|*arctg

36. Kryterium Nyquista - Warunkiem tego, by układ opisany transmitancją G był stabilny jest, aby wielomian mianownika funkcji G był wielomianem Hurwitz'a, co oznacza, że wielomian nie posiada zer w domkniętej prawej półpłaszczyźnie s.

Druga wersja twierdzenia o stabilności, - Jeżeli transmitancja układu otwartego nie ma biegunów w otwartej prawej półpłaszczyźnie, układ zamknięty jest stabilny gdy wykres Nyquista transmitancji G nie okrąża punktu (-1;j₀), ani nie przechodzi przez ten punkt

Def. Odległość między punktem (-1;j₀) oraz (G₀(jw_P);0) nazywamy zapasem wzmocnienia. Wyrażamy go w skali logarytmicznej.

Def. Niech w_P>0 będzie taką pulsacją, dla której moduł |G₀(jw_P)|=1. Jest to pulsacja, dla której |G₀(jw_P)|=1 przecina okrąg jednostkowy kąt między ujemną osią odciętych, a prostą przechodzącą przez punkt |G₀(jw_P)| w kierunku (0,0) nazywamy zapasem fazy. Stabilność układu oznacza, że zapas fazy i zapas wzmocnienia są większe od 0.

Zapas fazy = |<(-1)|-|<G₀(jw)|=180°-|<G₀(jw_P)|

37. poprawa własności dynamicznych i statycznych

38. Człon całkujący to człon, który na wyjściu daje sygnał y(t) proporcjonalny do całki sygnału wejściowego x(t):

Poddanie powyższego związku obustronnej transformacji Laplace'a daje związek pomiędzy transformatami obu sygnałów:
stąd: transmitancja członu całkującego ma postać:
Jego odpowiedź impulsowa wygląda następująco:
, charakterystyka skokowa: w dziedzinie operatorowej:
, w dziedzinie czasu:
charakterystyka amplitudowo-fazowa:
, charakterystyka fazowa:
, wzmocnienie maleje o 20 dB. Rzeczywisty człon całkujący
gdzie: k - wzmocnienie, T- stała czasowa

Spis treści:

1. Omów schemat funkcjonalny typowego układu sterowania automatycznego z pętlą sprzężenia zwrotnego.

2. Scharakteryzuj dwa podstawowe zadania realizowane w układach sterowania autom.-zadanie przestawiania i nadążania.

3. Opisz typowe sytuacje, w których projektant układów regulacji zmuszony jest do poszukiwania kompromisowych rozwiązań.

4. Wymień podstawowe modele liniowych obiektów dynamicznych (modele wej-wyj oraz model w przestrzeni stanu). Omów wzajemne związki między tymi modelami.

5. Opisz klasę równoważności podobnych modeli w przestrzeni

6. Zdefiniuj macierz fundamentalną liniowego jednorodnego r-nia

różniczkowego x'(t) = A*x(t) , x(t₀)∈Rⁿ. Opisz znane Ci sposoby wyznaczania takiej macierzy.

9. Co to jest „diagonalizacja“ modelu w przestrzeni stanu? Procedura takiej diagonalizacji. Czy każda macierz stanu da się zdiagonalizować?

10. Podaj definicje oraz BIBO stabilności liniowej obiektów dynamiczn.

11. Podaj definicję oraz kryterium stabilności asymptotycznej liniowego obiektu dynamicznego

12. Podaj definicje oraz kryterium stabilności wewnątrz liniowego obiektu dynamicznego

14. Zdefiniuj pojecie uchybu sterowania. Omów główne przyczyny pojawienia się uchybów. Jakie środki, aby ograniczyć wartość uchybu.

15. Podaj definicje astatyzmu I stopnia układu regulacji automatycznej.

16. Dany jest układ zamknięty z jednostkowym, ujemnym sprzężeniem zwrotnym, obejmującym tor główny złożony z szeregowo połączonych korektora G_c(s)=(s-1)/s oraz obiektu G_p(s)=2/(s-1). Dlaczego taki sposób korekcji jest niedopuszczalny?

17. Dany jest model: (rysunek) Podaj warunki, jakie należy nałożyć na wartości nastaw k oraz T, aby w tym układzie doprowadzić do zerowania się ustalonego uchybu położeniowego. Jaka będzie wówczas wartość ustalonego uchybu prędkościowego?

18. Wymień zasady wykreślania linii pierwiastkowych.

19. Uzasadnij reguły kreślenia LP

21. Scharakteryzuj pojęcie dobrej określoności liniowego układu dynamicznego. Podaj prosty przykład układu ze sprzężeniem zwrotnym, który nie jest dobrze określony. Zinterpretuj własności takiego układu w oparciu o metodę linii pierwiastkowych.

22. Omów bezpośrednie (w dziedzinie czasu) oraz pośrednie (w dziedzinie częstotliwości) wskaźniki jakości regulacji, odnoszące się do (i) stabilności układu zamkniętego oraz do (ii) szybkości procesów przejściowych w tym układzie.

23. Omów podstawowe charakterystyki oraz praktyczne wskaźniki opisujące człon dynamiczny pierwszego rzędu G(s) = k/(1+sT)

24. Omów podstawowe charakterystyki oraz praktyczne wskaźniki opisujące człon dynamiczny drugiego rzędu G(s) = k/[1+2(ts+t2s2)]

25. Scharakteryzuj prostą metodę syntezy układów regulacji, w której człon dynamiczny drugiego rzędu G(s) = k/[1+2(ts+t2s2)] wykorzystywany jest jako pewna wzorcowa funkcja przenoszenia (transmitancja)

26. Dany jest układ, w którym człon k=(s(1 + s)) w torze głównym objęty

jest jednostkowym ujemnym sprzężeniem zwrotnym. Zakładając, że k > 0 jest nastawą swobodną, rozważ wpływ wartości tej nastawy na własności (i) odpowiedzi skokowej oraz (ii) charakterystyki modułu rozważanego układu zamkniętego.

27. Opisz typ monotoniczności następujących praktycznych wskaźników jakości regulacji, odpowiadających wzorcowej funkcji przenoszenia drugiego rzędu …

28. Scharakteryzuj prostą metodę syntezy układów regulacji, opartą na koncepcji 'pary biegunów dominujących' wybranej funkcji przenoszenia projektowanego układu zamkniętego.

30. Uzasadnij tezę, która głosi, że obecność zer funkcji przenoszenia układu otwartego w prawej półpłaszczyźnie zespolonej może w istotny sposób ograniczać statyczną¡ dokładność regulacji, możliwą¡ do uzyskania w odpowiednim układzie zamkniętym.

31. Omów właściwości oraz zastosowanie korektora (regulatora) przyspieszającego fazę LEAD. Posługując się metodą linią pierwiastkowych oraz metodą charakterystycznych częstotliwościowych, podaj stosowne interpretacyjne motywujące użycie takiego korektora w układzie regulacji automatycznej. (rys.)

32. Omów własności oraz zastosowanie korektora (regulatora) opóźniającego fazę LAG. Posługując się metodą linii pierwiastkowych oraz metoda charakterystyk częstotliwościowych, podaj stosowne interpretacje motywujące użycie takiego korektora w ukł. regulacji auto.

34. Wyznacz orientacyjny przebieg charakterystyk Nyquista dla zadanych (prostych!) modeli (funkcji przenoszenia).

36. Podaj definicje zapasów (marginesów) wzmocnienia oraz fazy układu regulacji ze sprzężeniem zwrotnym. Interpretacje tych definicji w oparciu o charakterystyki Nyquista i Bodego otwartego układu regulacji.

37. Scharakteryzuj główne założenia metody korekcji liniowych układów dynamicznych ze sprzężeniem zwrotnym w oparciu o charakterystyki częstotliwościowe odpowiednich układów otwartych.

38. Omów rolę członu całkującego w korektorze dynamiki toru głównego układu regulacji. Przedstaw interpretacje w oparciu o linie pierwiastkowe oraz charakterystyki częstotliwościowe.

Spis treści:

1. Omów schemat funkcjonalny typowego układu sterowania automatycznego z pętlą sprzężenia zwrotnego.

2. Scharakteryzuj dwa podstawowe zadania realizowane w układach sterowania autom.-zadanie przestawiania i nadążania.

3. Opisz typowe sytuacje, w których projektant układów regulacji zmuszony jest do poszukiwania kompromisowych rozwiązań.

4. Wymień podstawowe modele liniowych obiektów dynamicznych (modele wej-wyj oraz model w przestrzeni stanu). Omów wzajemne związki między tymi modelami.

5. Opisz klasę równoważności podobnych modeli w przestrzeni

6. Zdefiniuj macierz fundamentalną liniowego jednorodnego r-nia

różniczkowego x'(t) = A*x(t) , x(t₀)∈Rⁿ. Opisz znane Ci sposoby wyznaczania takiej macierzy.

9. Co to jest „diagonalizacja“ modelu w przestrzeni stanu? Procedura takiej diagonalizacji. Czy każda macierz stanu da się zdiagonalizować?

10. Podaj definicje oraz BIBO stabilności liniowej obiektów dynamiczn.

11. Podaj definicję oraz kryterium stabilności asymptotycznej liniowego obiektu dynamicznego

12. Podaj definicje oraz kryterium stabilności wewnątrz liniowego obiektu dynamicznego

14. Zdefiniuj pojecie uchybu sterowania. Omów główne przyczyny pojawienia się uchybów. Jakie środki, aby ograniczyć wartość uchybu.

15. Podaj definicje astatyzmu I stopnia układu regulacji automatycznej.

16. Dany jest układ zamknięty z jednostkowym, ujemnym sprzężeniem zwrotnym, obejmującym tor główny złożony z szeregowo połączonych korektora G_c(s)=(s-1)/s oraz obiektu G_p(s)=2/(s-1). Dlaczego taki sposób korekcji jest niedopuszczalny?

17. Dany jest model: (rysunek) Podaj warunki, jakie należy nałożyć na wartości nastaw k oraz T, aby w tym układzie doprowadzić do zerowania się ustalonego uchybu położeniowego. Jaka będzie wówczas wartość ustalonego uchybu prędkościowego?

18. Wymień zasady wykreślania linii pierwiastkowych.

19. Uzasadnij reguły kreślenia LP

21. Scharakteryzuj pojęcie dobrej określoności liniowego układu dynamicznego. Podaj prosty przykład układu ze sprzężeniem zwrotnym, który nie jest dobrze określony. Zinterpretuj własności takiego układu w oparciu o metodę linii pierwiastkowych.

22. Omów bezpośrednie (w dziedzinie czasu) oraz pośrednie (w dziedzinie częstotliwości) wskaźniki jakości regulacji, odnoszące się do (i) stabilności układu zamkniętego oraz do (ii) szybkości procesów przejściowych w tym układzie.

23. Omów podstawowe charakterystyki oraz praktyczne wskaźniki opisujące człon dynamiczny pierwszego rzędu G(s) = k/(1+sT)

24. Omów podstawowe charakterystyki oraz praktyczne wskaźniki opisujące człon dynamiczny drugiego rzędu G(s) = k/[1+2(ts+t2s2)]

25. Scharakteryzuj prostą metodę syntezy układów regulacji, w której człon dynamiczny drugiego rzędu G(s) = k/[1+2(ts+t2s2)] wykorzystywany jest jako pewna wzorcowa funkcja przenoszenia (transmitancja)

26. Dany jest układ, w którym człon k=(s(1 + s)) w torze głównym objęty

jest jednostkowym ujemnym sprzężeniem zwrotnym. Zakładając, że k > 0 jest nastawą swobodną, rozważ wpływ wartości tej nastawy na własności (i) odpowiedzi skokowej oraz (ii) charakterystyki modułu rozważanego układu zamkniętego.

27. Opisz typ monotoniczności następujących praktycznych wskaźników jakości regulacji, odpowiadających wzorcowej funkcji przenoszenia drugiego rzędu …

28. Scharakteryzuj prostą metodę syntezy układów regulacji, opartą na koncepcji 'pary biegunów dominujących' wybranej funkcji przenoszenia projektowanego układu zamkniętego.

30. Uzasadnij tezę, która głosi, że obecność zer funkcji przenoszenia układu otwartego w prawej półpłaszczyźnie zespolonej może w istotny sposób ograniczać statyczną¡ dokładność regulacji, możliwą¡ do uzyskania w odpowiednim układzie zamkniętym.

31. Omów właściwości oraz zastosowanie korektora (regulatora) przyspieszającego fazę LEAD. Posługując się metodą linią pierwiastkowych oraz metodą charakterystycznych częstotliwościowych, podaj stosowne interpretacyjne motywujące użycie takiego korektora w układzie regulacji automatycznej. (rys.)

32. Omów własności oraz zastosowanie korektora (regulatora) opóźniającego fazę LAG. Posługując się metodą linii pierwiastkowych oraz metoda charakterystyk częstotliwościowych, podaj stosowne interpretacje motywujące użycie takiego korektora w ukł. regulacji auto.

34. Wyznacz orientacyjny przebieg charakterystyk Nyquista dla zadanych (prostych!) modeli (funkcji przenoszenia).

36. Podaj definicje zapasów (marginesów) wzmocnienia oraz fazy układu regulacji ze sprzężeniem zwrotnym. Interpretacje tych definicji w oparciu o charakterystyki Nyquista i Bodego otwartego układu regulacji.

37. Scharakteryzuj główne założenia metody korekcji liniowych układów dynamicznych ze sprzężeniem zwrotnym w oparciu o charakterystyki częstotliwościowe odpowiednich układów otwartych.

38. Omów rolę członu całkującego w korektorze dynamiki toru głównego układu regulacji. Przedstaw interpretacje w oparciu o linie pierwiastkowe oraz charakterystyki częstotliwościowe.

Spis treści:

1. Omów schemat funkcjonalny typowego układu sterowania automatycznego z pętlą sprzężenia zwrotnego.

2. Scharakteryzuj dwa podstawowe zadania realizowane w układach sterowania autom.-zadanie przestawiania i nadążania.

3. Opisz typowe sytuacje, w których projektant układów regulacji zmuszony jest do poszukiwania kompromisowych rozwiązań.

4. Wymień podstawowe modele liniowych obiektów dynamicznych (modele wej-wyj oraz model w przestrzeni stanu). Omów wzajemne związki między tymi modelami.

5. Opisz klasę równoważności podobnych modeli w przestrzeni

6. Zdefiniuj macierz fundamentalną liniowego jednorodnego r-nia

różniczkowego x'(t) = A*x(t) , x(t₀)∈Rⁿ. Opisz znane Ci sposoby wyznaczania takiej macierzy.

9. Co to jest „diagonalizacja“ modelu w przestrzeni stanu? Procedura takiej diagonalizacji. Czy każda macierz stanu da się zdiagonalizować?

10. Podaj definicje oraz BIBO stabilności liniowej obiektów dynamiczn.

11. Podaj definicję oraz kryterium stabilności asymptotycznej liniowego obiektu dynamicznego

12. Podaj definicje oraz kryterium stabilności wewnątrz liniowego obiektu dynamicznego

14. Zdefiniuj pojecie uchybu sterowania. Omów główne przyczyny pojawienia się uchybów. Jakie środki, aby ograniczyć wartość uchybu.

15. Podaj definicje astatyzmu I stopnia układu regulacji automatycznej.

16. Dany jest układ zamknięty z jednostkowym, ujemnym sprzężeniem zwrotnym, obejmującym tor główny złożony z szeregowo połączonych korektora G_c(s)=(s-1)/s oraz obiektu G_p(s)=2/(s-1). Dlaczego taki sposób korekcji jest niedopuszczalny?

17. Dany jest model: (rysunek) Podaj warunki, jakie należy nałożyć na wartości nastaw k oraz T, aby w tym układzie doprowadzić do zerowania się ustalonego uchybu położeniowego. Jaka będzie wówczas wartość ustalonego uchybu prędkościowego?

18. Wymień zasady wykreślania linii pierwiastkowych.

19. Uzasadnij reguły kreślenia LP

21. Scharakteryzuj pojęcie dobrej określoności liniowego układu dynamicznego. Podaj prosty przykład układu ze sprzężeniem zwrotnym, który nie jest dobrze określony. Zinterpretuj własności takiego układu w oparciu o metodę linii pierwiastkowych.

22. Omów bezpośrednie (w dziedzinie czasu) oraz pośrednie (w dziedzinie częstotliwości) wskaźniki jakości regulacji, odnoszące się do (i) stabilności układu zamkniętego oraz do (ii) szybkości procesów przejściowych w tym układzie.

23. Omów podstawowe charakterystyki oraz praktyczne wskaźniki opisujące człon dynamiczny pierwszego rzędu G(s) = k/(1+sT)

24. Omów podstawowe charakterystyki oraz praktyczne wskaźniki opisujące człon dynamiczny drugiego rzędu G(s) = k/[1+2(ts+t2s2)]

25. Scharakteryzuj prostą metodę syntezy układów regulacji, w której człon dynamiczny drugiego rzędu G(s) = k/[1+2(ts+t2s2)] wykorzystywany jest jako pewna wzorcowa funkcja przenoszenia (transmitancja)

26. Dany jest układ, w którym człon k=(s(1 + s)) w torze głównym objęty

jest jednostkowym ujemnym sprzężeniem zwrotnym. Zakładając, że k > 0 jest nastawą swobodną, rozważ wpływ wartości tej nastawy na własności (i) odpowiedzi skokowej oraz (ii) charakterystyki modułu rozważanego układu zamkniętego.

27. Opisz typ monotoniczności następujących praktycznych wskaźników jakości regulacji, odpowiadających wzorcowej funkcji przenoszenia drugiego rzędu …

28. Scharakteryzuj prostą metodę syntezy układów regulacji, opartą na koncepcji 'pary biegunów dominujących' wybranej funkcji przenoszenia projektowanego układu zamkniętego.

30. Uzasadnij tezę, która głosi, że obecność zer funkcji przenoszenia układu otwartego w prawej półpłaszczyźnie zespolonej może w istotny sposób ograniczać statyczną¡ dokładność regulacji, możliwą¡ do uzyskania w odpowiednim układzie zamkniętym.

31. Omów właściwości oraz zastosowanie korektora (regulatora) przyspieszającego fazę LEAD. Posługując się metodą linią pierwiastkowych oraz metodą charakterystycznych częstotliwościowych, podaj stosowne interpretacyjne motywujące użycie takiego korektora w układzie regulacji automatycznej. (rys.)

32. Omów własności oraz zastosowanie korektora (regulatora) opóźniającego fazę LAG. Posługując się metodą linii pierwiastkowych oraz metoda charakterystyk częstotliwościowych, podaj stosowne interpretacje motywujące użycie takiego korektora w ukł. regulacji auto.

34. Wyznacz orientacyjny przebieg charakterystyk Nyquista dla zadanych (prostych!) modeli (funkcji przenoszenia).

36. Podaj definicje zapasów (marginesów) wzmocnienia oraz fazy układu regulacji ze sprzężeniem zwrotnym. Interpretacje tych definicji w oparciu o charakterystyki Nyquista i Bodego otwartego układu regulacji.

37. Scharakteryzuj główne założenia metody korekcji liniowych układów dynamicznych ze sprzężeniem zwrotnym w oparciu o charakterystyki częstotliwościowe odpowiednich układów otwartych.

38. Omów rolę członu całkującego w korektorze dynamiki toru głównego układu regulacji. Przedstaw interpretacje w oparciu o linie pierwiastkowe oraz charakterystyki częstotliwościowe.

Written by RelaX Team®

January 2006/2007

1/s

K

m

1/s

K

---