Stała dielektryczna różnych materiałów

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie stałej dielektrycznej powietrza (próżni) i materiału PCV.

2. Przebieg ćwiczenia

Pomiar bezwzględnej stałej dielektrycznej dla „próżni”
:

Pomiaru dokonujemy poprzez zmianę odległości d pomiędzy okładkami (próżniowego) kondensatora płaskiego, przy ustalonym stałym napięciu
. Pomiaru ładunku Q na okładkach kondensatora dokonujemy w sposób pośredni wykorzystując zależność Q=UC. W drugiej serii pomiarów w tej części ćwiczenia wykonujemy sprawdzenie zależności pomiędzy ładunkiem Q, a różnicą potencjałów
, jaka pojawi się między okładkami kondensatora. Z nachylenia prostej Q=f(
) można uzyskać wartość stałej dielektrycznej
. Następnie czynności wykonywane w drugiej serii pomiarów wykonujemy kiedy między okładkami znajduje się tworzywo sztuczne PCV

3. Pomiary i obliczenia

Pomiar bezwzględnej stałej dielektrycznej dla próżni

S=0,0531

=1,5kV C=220nF

U [V]	1.3	1.5	1.8	2.2	2.6	3.8
d [cm]	0.35	0.30	0.25	0.20	0.15	0.10
1/d [cm ]	2.86	3.33	4	5	6.67	10
Q=CU [nC]	286	330	396	484	572	836

Ładunek elektryczny Q kondensatora płaskiego w funkcji odwrotności odległości pomiędzy płytami kondensatora

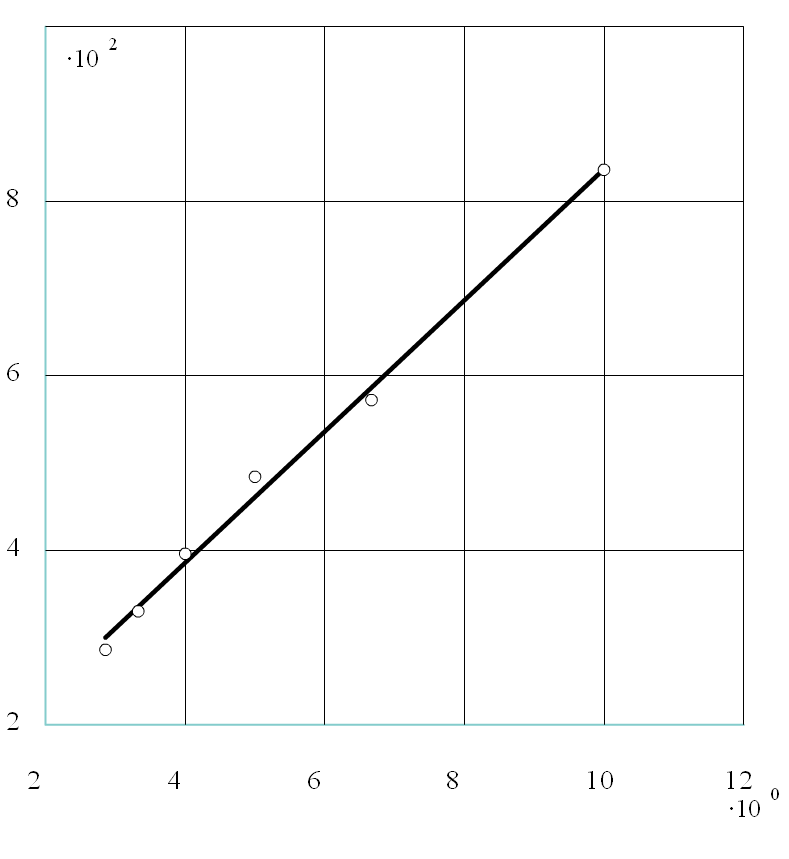
Mając powyższe wyniki pomiarów i wykres możemy z nachylenia prostej z wykresu Q=f(1/d) uzyskać wartość stałej dielektrycznej dla próżni
.

Równanie otrzymanej prostej:

Q=(CU=
(S/d)
)=
S
(1/d)

=[Q/(1/d)]*[1/(S
)]

Przy czym Q/(1/d)=a

- obliczamy z najmniejszej sumy kwadratów

= 75,20

= 2,74

korelacja = 0,997

Następnie podstawiając do równania:

=[(Qd)/(S
)]

=75,20
[n C cm
]

=0,94 * 10^-4 [
]

=0,94 * 10^-11 [
]

=9,4 * 10^-12 [
]

Teraz obliczamy błąd względny:

=±(
)

=±(2,74/75,20+ 10/531 + 0.1/1.5)=+(0.036+0,019 +0,067)

=±0,122

Obliczamy błąd bezwzględny:

= 1,1468* 10^-12

Wynik:

=(9,4±1,1468)*10^-15 [
]

Druga seria pomiarów

S=0,0531
d=0,002m C=220nF

U [kV]	0,5	1	1,5	2	2,5	3	3,5	4
U [V]	0,6	1,3	2,1	2,8	3,6	4,6	5,6	7,0
Q=CU [nC]	132	286	462	616	792	1012	1232	1540

Ładunek elektrostatyczny Q kondensatora płaskiego w funkcji przyłożonego napięcia Uc

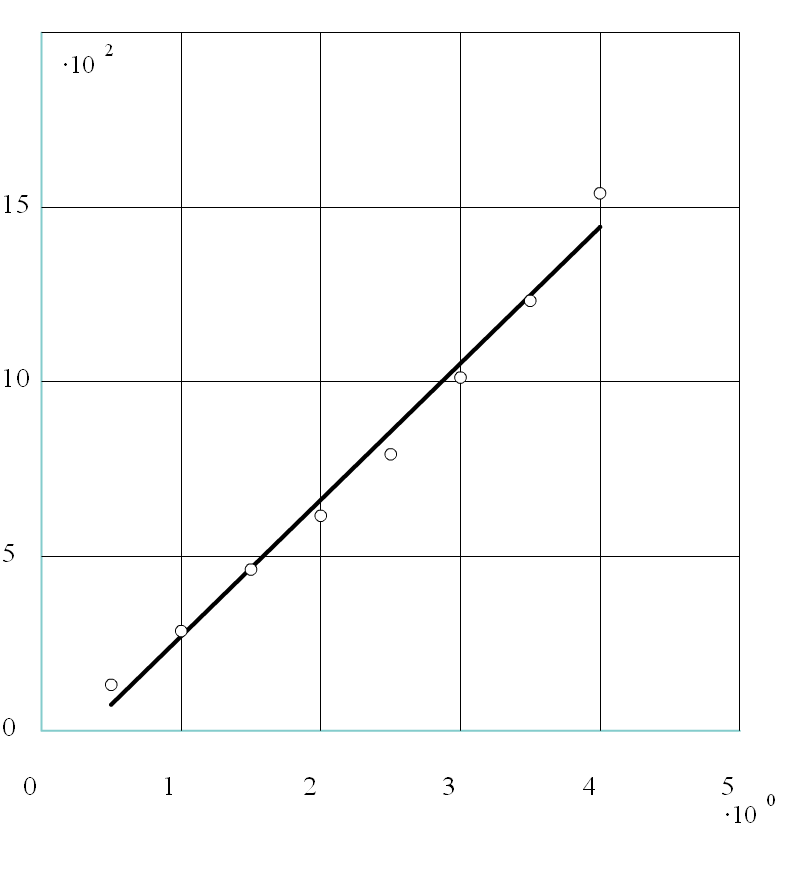
= 390,76

= 18,26

korelacja = 0,993

=[(Qd)/(S
)]

= 4,9 * 10^-4[
]

Błąd względny:

=±(
)=±(18,26/390,76+10/531+0,01/0,2)

=±(0,047+0,019+0,05)

=±0,116

Błąd bezwzględny:

=0,116*4,9*10^-4 [
]

=0,5684 *10^-4 [
]

Wynik:

=(4,9,±0,5684) *10^-4[
]

Pomiary bezwzględnej stałe dielektrycznej dla tworzywa sztucznego - PCV

S=0,0531
d=1cm C=220nF

U [kV]	0,5	1	1,5	2	2,5	3	3,5	4
U [V]	0,5	0,86	1,3	1,7	2,3	2,6	3,0	3,5
Q=CU [nC]	110	189,2	286	374	506	572	660	880

Ładunek elektrostatyczny kondensator płaskiego w funkcji przyłożonego napięcia Uc

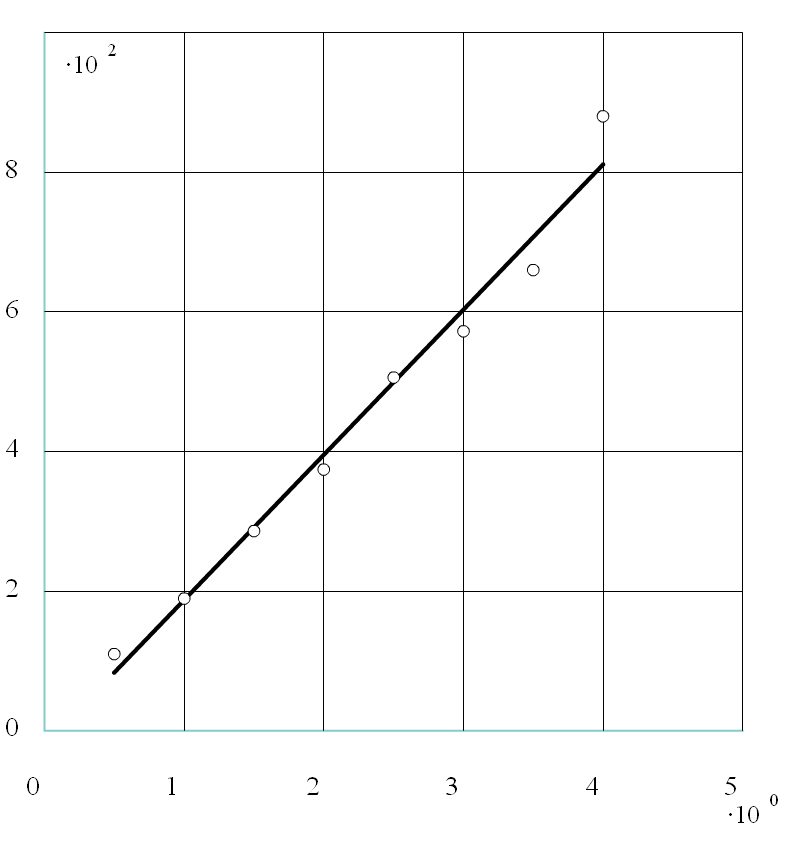
=207,95

=12,07

korelacja - 0,990

Q=

(S/d)

=
(d/S)

=

Błąd względny:

=±(
)=±(12,07/207,95+10/531+0,01/1)

=±(0,058+0,019+0,01)

=±0,087

Błąd bezwzględny:

=

Wynik dla bezwzględnej stałej dielektrycznej podajemy w postaci:

=[
]

=
=

=+(
)=+()

=±

=

=

Wynik dla względnej starej dielektrycznej:

=

4. Wnioski

Błędy w wynikach pomiarów mogły występować z różnych powodów takich jak: niedokładności zmierzenia średnicy powierzchni okładek. Błędy mogły również wyniknąć z tego, że co pomiar musieliśmy rozładowywać kondensator. Także nasza odległość od kondensatora mogła wpłynąć na uzyskiwane wyniki. Nasz wynik dla stałej dielektrycznej dla próżni nie wyszedł zbliżony do wartości tablicowej.

U_c[kV]

Q[nC]

Q[nC]

Q[nC]

1/d[cm]

U_c[kV]

---