Ciała materialne występują w przyrodzie w zależności ok. warunków ciśnienia i temperatury w 3 stanach skupienia: stałym, ciekłym i gazowym.

PŁYNEM nazywamy ciało materialne, które charakteryzuje się dużą ruchliwością cząstek, dzięki której podlega łatwo odkształceniom pod wpływem nawet znikomych sił zewnętrznych przyłożonych do tego ciała i przyjmuje kształt naczynia w którym się znajduje. Płyny dzielimy na ciecze i gazy.

1.Cechy charakterystyczne cieczy: samoistna objętość, bardzo mała ściśliwość (zakładamy, że są one nieściśliwe), tworzą tka zwana powierzchnię swobodną (pow. Rozdzielająca ciecz od gazu)

Cechy charakterystyczne gazów: brak samoistnej objętości, wypełniają całkowicie naczynie do którego zostały wprowadzone, duża ściśliwość, sprężystość objętościowa, nie tworzą powierzchni swobodnej.

2 Płyn jako środek ciągły. (kontinuum matematyczne) środek ciągły czyli bryła geometryczna zawierająca nieskończoną ilość cząsteczek wypełniającą tą objętość w sposób ciągły, jednolity. Umożliwia to wyodrębnienie takiej objętości w otoczeniu p-ktu M nieskończenie małych elementów płynu i następnie przez przejście z ich wymiarami
do

granicy zero stosowanie aparatu analizy matematycznej.

ELAMANTEM PŁYNU rzeczywistego nazywać będziemy taką jego objętość
której wymiary liniowe są wielkościami małymi wyższego rzędu w stosunku do wymiarów naczynia objętości V, w której znajduje się płyn ale która z drugiej strony zawiera tak dużą liczbę cząsteczek materialnych, że właściwości makroskopowe płynu odniesione do tej objętości zachowuję swój sens fizykalny.

Makroskopowe właściwości płynu

Rodzaje pól wielkości fizycznej: Pole H nazywać będziemy jednorodnym jeżeli:

Niejednorodnym jeżeli chociaż jedna zmienna nie równa się 0

Stacjonarnym, ustalonym jeżeli pochodna cząstkowa względem czasu

niestacjonarnym, nieustalonym jeżeli

w polu niejednorodnym, w polu jednorodnym

ściśliwość płynu zdolność do zmniejszania pierwotnej objętości płynu w skutek działania sił zewnętrznych, miara:

WSPÓŁCZYNNIK ŚCIŚLIWOŚCI

(znak „-„ wynika z tego, że dodatni przyrost ciśnienia powoduje ujemny przyrost objętości), p - ciśnienie

MODUŁ SPRĘŻYSTOŚCI PŁYNU

,
T- temperatura

3. Jedna z podstawowych właściwości poruszającego się płynu rzeczywistego jest pewien na ogół niewielki opór stawiany siłom zewnętrznym. Siły te wywołują w płynie naprężenia styczne, które stanowią istotę lepkości lub tarcia wewnętrznego

LEPKOŚĆ zdolność płynu rzeczywistego do przenoszenia naprężeń stycznych podczas jego ruchu.

Istotną cechą wyróżniającą płyn od ciała stałego jest to, że pod wpływem przyłożonych sił zewnętrznych płynie. Miara jest dynamiczny wsp lepkości będący proporcjonalności w „Hipotezie Newtona”
,

PŁYNIĘCIE pod wpływem przyłożonego stałego naprężenia stycznego następuje przyrost odkształcenia postaciowego w czasie.

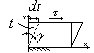
„Hipotezie Newtona” dla płynów doskonale lepkich prędkość z jaką narasta jest wprost proporc. do naprężenia stycznego

kąt odkształcenia postaciowego

szybkość ścinania

szybkość ścinania jest pochodną
względem normalnej do kierunku ścinania. W przypadku prostego ścinania hipotezy Newtona przyjmuje postać:

4. Modele płynów

płyn doskonały - fikcyjny płyn nieściśliwy odznaczający się

zupełnym brakiem lepkości

gaz doskonały - ściśliwy płyn doskonały nie przenoszący naprężeń stycznych ale spełniający dodatkowo równanie stanu płynu doskonałego

5. Powierzchnia kontrolna dowolna otwarta lub zamknięta powierzchnia w polu prędkości płynu odznaczająca się tym, że położenia każdego jej punktu nie ulega zmianie względem przyjętego układu współrzędnych (x,y,z)

powierzchnię kontrolna tworzą wciąż te same punkty w przestrzeni natomiast znajdować się na niej mogą w miarę upływu czasu inne elementy płynu (traktowane jako punkty materialne)

obszar kontrolny - obszar przepływu ograniczony zamkniętą powierzchnią kontrolną

powierzchnia płynna - dowolna powierzchnia w polu przepływu charakteryzująca się tym, że tworzą ją stale te same punkty materialne płynu (cząsteczki), natomiast jej kształt i położenie względem przyjętego układu odniesienia mogą ulegać zmianie pod wpływem czasu

6. Siły działające na płyn

- masowe
- jednostkowa siła masowa

;

X,Y,Z funkcje opisujące zależności położenia

wersory osi x,y,x

- powierzchniowe - rozłożone są w sposób równomierny i ciągły na powierzchni na którą działają, występują w formie naprężeń lub ciśnień.

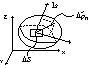
a)wewnętrzne - występujące na wyodrębnionych myślowo powierzchnie wewnątrz obszaru ego płynu, może to być ciśnienie, tarcie wewnętrzne.

b)zewnętrzne - występujące między ściankami naczynia a wypełniającym je płynem lub ciałem stałym i opływającym go płynem

indeks „n” oznacza, że jest to siła, która działa na element powierzchni do którego normalną jest n. W punkcie M możemy zdefiniować naprężenie
na element powierzchniowy, którego normalną jest n

! naprężenie jest zorientowane w przestrzeni !

drugi indeks oznaczać będzie kierunek rzutowania podstawowego wektora
:

w przypadku gdy płyn znajduje się w stanie spoczynku (równowagi)lub gdy płyn jest doskonały

w tych dwóch przypadkach
gdzie

p- ciśnienie hydrostatyczne. „-” wynika z tego, że płyn nie przenosi naprężeń rozciągających

7. stan naprężenia płynu

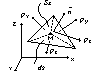
M(x,y,z)

,
- tensor naprężeń

;

- cosinusy kierunkowe

do opisania stanu naprężenia płyty w wybranym punkcie M trzeba podać 9 liczb, nazywanych składowymi naprężenia
są to trzy składowe normalne
oraz 6 składowych stycznych.

Zgodnie z postulatem Boltzmana tensor naprężenia jest symetryczny tzn.
;
;

Twierdzenie Eulera Załóżmy, ze płyn znajduje się w równowadze lub jest to płyn doskonały poruszający się. Naprężenia styczne są równe zero. M(x,y,z)

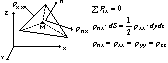
Ciśnienie w punkcie M nie zależy od orientacji poprowadzonej przez ten punkt. Ciśnienie hydrostatyczne p nie zależy od orientacji elementu powierzchniowego przechodzącego przez dany punkt M(x,y,x). Cisnienie jest skalarem, naprężenie tensorem rzędu drugiego!!!!

8. równaniu ruchu płynu rzeczywistego przez naprężenia

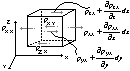
M(x,y,z) M`(x+dx,y+dy,z+dz)

Zaznaczymy składowe w kierunku wybranej osi i dokonamy ich bilansu.

Zgodnie z zasada d'Alamberta robimy bilans sił w kierunku x

po podzieleniu przez
i uporządkowaniu

podstawowe równania ruchu płynu wyrażone w naprężeniach

przypadki szczególne równań różniczkowych ruchu

- płyn doskonały
i zgodnie z tw Eulera

równania Eulera ruchu płynu doskonałego

- płyn w stanie równowagi

równania różniczkowe równowagi płynu

KINEMATYKA PŁYNÓW

Metody badania ruchu płynów

- Metoda Lagrange`a (analiza wędrowna)

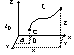
x=x(a,b,c,t) zmienne Lagrange`a

polega na tym, że ruch wybranego elementu płynu opisuje obserwator poruszający się wraz z ta cząsteczką, natomiast wybrany element płynu traktowany jest indywidualnie. Obserwator rejestruje zmiany nie tylko położenia elementu płynu w przestrzeni ale również wszystkie zmiany innych własności fizycznych zachodzących w upływie czasu. Celem wyróżnienia elementu płynu z pośród niezliczonej ilości elementów płynu należy podać jego współrzędne (a,b,c) w chwili t₀. Kazda zmiana którejkolwiek współrzędnej a,b,c oznacza przejście do innego elementu płynu.

W dowolnej chwili czasu t położenie wybranego elementu płynu opisane jest za pomocą tzw współrzędnych Langrange`a
obliczamy pochodne cząstkowe !

- Metoda Eulera (analiza lokalna)

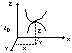
polega na tym, że w wydzielonym obszarze pszestrzeni z poruszającym się płynem zbiór punktów M i badamy jakim zmianom z upływem czasu podlegają prędkości lub inne wielkości fizyczne różnych elementów płynu przechodzących przez ten punkt w przestrzeni.

W metodzie Eulera ruch jest kinematycznie określony gdy dane jest pole prędkości

W przeciwieństwie do metody Lagrange`a zmienne x,y,z,t są równoprawne (tego samego typu) H=H(x,y,z,t)

całość zmian wielkości H opisuje tzw pochodna materialna przy czym jest ona sumą dwóch pochodnych: konwercyjnej (unoszenia) i lokalnej.

Pochodna konwercyjna przedstawia zmiany danej wielkości H przy przejściu z punktu M(x,y,z) do sąsiadującego punktu M`(x+dx,y+dy,z+dz) w czasie dt

Pochodna lokalna opisuje zmiany wielkości H jakie zachodzą w czasie dt w wybranym punkcie M(x,y,z)

10. tor elementu płynu. Linia prądu

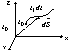
tor elementu - krzywa która jest miejscem goemetrycznym kolejnych położeń elementów płynu z upływem czasu.

;

;
równania różniczkowe toru elementu płynu.

Linia prądu - linia pola wektorowego prędkości albo inaczej jest to pomyślana linia przepływu składająca się z różnych elementów płynu w której w każdej chwili wektor prędkości jest styczny do krzywej.

Warunkiem zaistnienia tej krzywej jest spełnienie

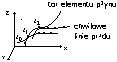
w odróżnieniu od toru elementu płynu kształt lini prądu przechodzącej przez wybrany punkt M(x,y,z) zależy w ogólnym przypadku od kształtu czasu t.

Tylko w przypadku ruchu ustalonego linie prądy pokrywają się z torami płynu. W ogólnym przypadku ruchu nieustalonego tor elementu płynu jest obwiednią chwilowych lini prądu.

Dwie linie prądu nei mogą na ogół się ze sobą przecinać istnieją jednak przypadki szczególne:

1. 
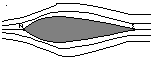
   V=0

2. 
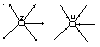
   V=+
   V=-
   

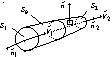
Powierzchnia prądu - powierzchnia która jest miejscem geometrycznym chwilowych linii prądu

W przypadku, gdy w przekroju poprzecznym kontur powierzchni prądu jest zamknięty to powierzchnię prądu nazywamy rurką prądu.

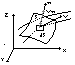
Struga płynu - podobszar płynu zawarty w rurze prądu

;
;

Objętościowe natężenie przepływu jest to objętość przepływająca w jednostce czasu przez powierzchnię S

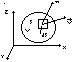
zgodnie z tw Green możemy wydatek przedstawić jako wydatek masowy (masowe natężenie przepływu)

;

Równanie ciągłości - matematyczny zapis rów ciągłości w odniesieniu do pewnego obszaru kontrolnego.

masa płynu zawarta w obs kontrol. w chwili t

- elementarny przyrost masy w obszarze kontrolnym wywołany zmianą gęstości płynu w czasie dt

- zmiana zwrotu wektora V

- elementarny przyrost masy w obszarze kontrolnym wynikający z nadwyżki masy wpływającej nad wypływającą
;

wobec dowolności obszaru całkowania równanie powyższe będzie spełnione tylko wtedy gdy funkcja podcałkowa przyjmie wartość zero.

Równanie ciągłości

Szczególne przypadki równania ciągłości:

a) ruch płynu ściśliwego jest ustalony

b) ruch nieściśliwego płynu
=const

;
jeżeli div jest równe zero to znaczy, że pole jest bez źródeł

Równanie ciągłości w przypadku ustalonego przepływu jednowymiarowego

;

Z równania tego wynika, że wydatek masowy (objętościowy) musi mieć wartość stałą w dowolnym wybranym przekroju poprzecznym przewodu.

Musi być zachowana ciągłość strugi płynu.

W przypadku płynu nieściśliwego

Wydatek masowy przyjmuje wartość stałą w dowolnym wybranym przekroju strugi.

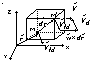
Ruch elementu płynu Stan prędkości odkształcenia w płynie.

M(x,y,x); M`(x+dx,y+dy,z+dz)

Tensor prędkości względnej

- prędkość kątowa

Twierdzenie Helmholtza - prędkość danego punktu płynu jest suma geometryczną prędkości ruchu postępowego, prędkości ruchu obrotowego i prędkości odkształcenia

DYNAMIKA PŁYNU DOSKONAŁEGO

Równanie Eulera

Równanie Bernouliego

Chcąc uzyskać równanie Bernouliego należy scałkować równania różniczkowe Eulera przy następujących założeniach upraszczających:

• ruch odbywa się w polu grawitacyjnym ziemskim

X=Y=0 , Z=-g

• ruch odbywa się wzdłuż określonej linii prądu
  

• ruch jest ustalony
  

• płyn jest parotropowy tzn istnieje tak funkcja P(x,y,z) ze jej pochodne cząstkowe

- równanie Bernouliego

W interpretacji fizykalnej równanie Bernouliego wyraża zasadę zachowanie energii w strudze elementarnej

równanie zasady zachowania en

Interpretacja geometryczna równania Bernouliego

wysokość prędkości

wysokość ciśnienia

z wysokość niwelacyjna (położenia)

Zastosowanie zasady pędu w mechanice płynów

Założenia: ruch jest ustalony, płyn jest niesciśliwy

;
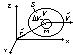
- elementarny pęd

,

- wektor sił zewnętrznych działających na ten obszar płynu

itp. We wzorze mają być bez strzałek u góry

stosujemy tw Greena

- reakcja hydrodynamiczna (wekror odwrotny do
)

=-

Reakcja hydrodynamiczna na ściankę krzywaka

Zał: ruch ustalony, płyn jest nieściśliwy

,

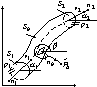
, Q- objętościowe natężenie przepływu

Zasada krętu

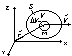
zał:

- wektor
- moment redukcyjny

DYNAMIKA PŁYNÓW RZECZYWISTYCH

- dynamiczny wsp lepkości, D - średnica

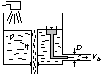
Ruch laminarny zwiększamy h ruch turbulentny

W ruchu burzliwym występuje fluktacja prędkości (składowe prędkości są zmiene)

Liczba Reynoldsa (bezwymiarowa liczba)

- kinematyczny wsp lepkości

Reynolds zauważył po raz pierwszy, że bezwymiarowe wyrażenie Re charakteryzuje w sposób jednoznaczny rodzaj przepływu

W przypadku

jedyną formą przepływu jest tzw ruch laminarny (zabarwiona struga cieczy nie miesza się z cieczą bezbarwną) czyli wszystkie elementy płynu poruszają się równolegle do głównego kierunku przepływu. Nie następuje przy tym makroskopowa wymiana pędu i masy między sąsiadującymi warstewkami cieczy

W przypadku

ma miejsce forma przejściowa ruchu

Powyżej
jedyną statyczną formą przepływu jest ruch turbulentny. Struga zabarwionej cieczy ulega gwałtownemu rozproszeniu w cieczy bezbarwnej co oznacza, że w zakresie tym występuje intensywna makroskopowa wymiana między masy między sąsiadującymi warstewkami

Równania ruchu

Równania konstytutywne (związki fizyczne)

- hipoteza Newtona

mnożymy przez 2 bo przy dewiatorze jest ½

Zgodnie z uogólnioną hipotezą Newtona dewiator naprężenia jest wprost proporcjonalny do dewiatora prędkości odkształcenia

Wynika z niej 6 równań konstytutywnych:

Naveir - Stokes'a równania

Równania różniczkowe nuchu naprężeń, równanie ciągłości i konstytutywne tworzą zamknięty układ 10 równań z 10 niewiadomymi. Wyeliminujmy składowe naprężenia

najbardziej ogólne równania płynu w zakresie laminarnym:

W szczególnym przypadku:

Równania Navier - Stokes'a w ukł cylindrycznym

gdzie

Równanie Bernouliego dla strugi płynu rzeczywistego

- wsp Coliorisa (korygujący energie kinetyczną)

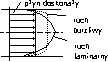
- laminarny,
- turbulentny

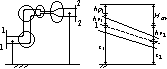
Liniowy przepływ cieczy w rurze o stałym przekroju kołowym

• rozkład naprężeń stycznych

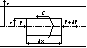
zał: p=p(x),

- przypadek ogólny

Przepływ ustalony i izometryczny

Dp/dx=const=C,

- strata cisnienia

- spadek ciśnienia

Prawo rozkładu naprężeń stycznych

- naprężenie styczne na ściance

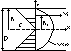
Rozkład prędkości

(„-„ ze wz R prędkość maleje)

;
;

warunki brzegowe: r=R; v=0

Objętościowe natężenie przepływu

Prawo Hogen'` - Poiseuille'a

Q - wydatek

- prawo Hogen'a Poiseuille`a

do wyznaczania dynamicznego lub kinematycznego wsp tarcia

Średnia prędkość przepływu

;
;

Obliczanie strat wywołanych tarciem wewnętrznym

Równanie DRCY`EGO

;

1.
strata ciśnienia

2.
- spadek ciśnienia

- r. Wymiarowe (strukturalne)

- wsp Fanning`a

- wsp oporu przepływu

3.
- wysokość strat

4.
- spadek hydrauliczny

;

- zależność funkcyjna
w zakresie laminarnym przy przepływie cieczy w rurach gładkich

;

porównujac równania stronami:

- zależność funkcyjna
w zakresie turbulentnym przy przepływie cieczy w rurach gładkich 3100<Re<10^5

- formuła Blasiusa

- wzór Kamana - Prandtla

dla 3100<Re<3,6*10^6

- wzór Nikuradse

Straty tarcia wewnętrznego w rurach chropowatych

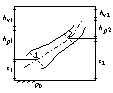
Wykres Nikuradse

- wsp chropowatości wzglednej

w przypadku rur chropowatych

lgy=lga+nlgx ;

W zakresie laminarym
nie ma wpływy więc

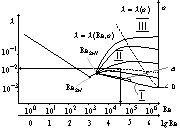
a - równanie Blasiusa

b - równanie Nikuradse, równanie Karmana - Prandtla

Strefy:

I - rury gładkie; II - o przejściowej chropowatości; III - chropowateRodzinę krzywych oporów w zakresie turbulentnym opisuje wzór Waldena

;

Obliczanie strat miejscowych

;
- wsp strat miejscowych =0,7

Przybliżona metoda obliczania
przy przekrojach wielokołowych

(z wyjątkiem wzoru Hagena - poiseuille`a)

- średnica zastępcza

- promień chydrauliczny

S =ab- przekrój cieczy

=2(a+b) - obwód zwilżany cieczą

---