22. Określenie ciągu funkcyjnego. Zbieżność punktowa i jednostajna ciągu funkcyjnego.

Definicja ciągu funkcyjnego

Ciągiem funkcyjnym określonym na zbiorze
nazywamy każdą funkcję odwzorowującą zbiór
w zbiór
. Załóżmy, że
. Wówczas dla oznaczenia ciągu funkcyjnego, którego n-tym wyrazem jest funkcja
używamy oznaczenie
. Niech
oznacza ciąg funkcyjny taki, że
. Niech
.

Definicja zbieżności punktowej ciągu funkcyjnego

Mówimy, że ciąg
jest punktowo zbieżny na zbiorze
do funkcji
jeśli

Definicja zbieżności jednostajnej ciągu funkcyjnego

Mówimy, że ciąg
jest jednostajnie zbieżny na zbiorze
do funkcji
jeśli .

Twierdzenie:

Przykład:

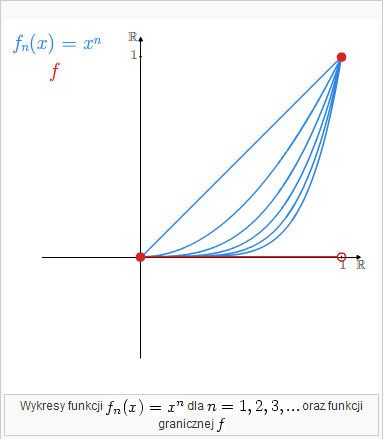
Niech
Wtedy
dla

Ciąg ten nie jest natomiast jednostajnie zbieżny.

Twierdzenie Weierstrassa

Niech

Twierdzenie

Jeśli
jest ciągła na X, to również f jest ciągła na X. Zwykła zbieżność nie implikuje przenoszenia ciągłości.

---