1. Cel ćwiczenia

Celem ćwiczenia jest badanie dźwięku wydawanego przez różne źródła, badanie zmian widma zachodzących przy zmianie warunków wzbudzenia źródła dźwięku.

2. Wprowadzenie:

Fale akustyczne - obiekt wykonujący drgania powoduje okresowe ruchy cząsteczek otaczającego go gazu (zwykle powietrza) będące z nim w bezpośrednim kontakcie. Cząsteczki te, działając siłami molekularnymi, pobudzają do drgań kolejne cząsteczki gazu. W gazie otaczającym drgający obiekt powstaje i rozchodzi się zaburzenie polegające na tworzeniu się okresowych zagęszczeń i rozrzedzeń gazu. Zaburzenie to zwane jest falą akustyczną. Częstotliwość rozchodzącej się w gazie fali akustycznej równa jest częstotliwości drgań źródła.

Fala akustyczna jest falą podłużną.

3. Dźwięk, Widmo dźwięku

Źródłem fali akustycznej może stać się każde sprężyste ciało pobudzone do drgań przez uderzenie, szarpnięcie, potarcie itp. Najczęściej wzbudzone źródło wykonuje jednocześnie wiele niezależnych drgań o różnych amplitudach amplitudach częstotliwościach. Częstotliwości i amplitudy poszczególnych drgań źródła, zależą od cech źródła. tzn. jego wielkości, kształtu, rodzaju materiału z jakiego jest wykonane, sposobu zamocowania, a także os sposobu pobudzenia go do drgań. Każdy rodzaj drgań źródła generuje związaną z nim falę akustyczną. Fala akustyczna, rozchodząca się w ośrodku otaczającym źródło powstaje ze złożenia tych fal. Fala ta na ogół ma przebieg okresowy niesinusoidalny i zwana jest dźwiękiem.

Analiza harmoniczna dźwięku polega na ustaleniu jakie są częstotliwości i amplitudy drgań harmonicznych składających się na dany dźwięk. Do tego celu używa się różnego typu rezonatorów akustycznych. Rezonator „wychwytuje” z badanego dźwięku złożonego ton harmoniczny o określonej częstotliwości. Analizę harmoniczną dźwięku można też przeprowadzić „od końca” metodą FFT (Fast Fourier Transform). Metoda ta (w uproszczeniu) polega na obliczeniu ilu i jakich tonów harmonicznych należałoby użyć, aby pop ich złożeniu otrzymać dźwięk jak najbardziej zbliżony do badanego dźwięku.

W wyniku analizy harmonicznej otrzymuje się tzw. widmo dźwięku. Widmo dźwięku zwykle przedstawia się w postaci wykresu prążkowego. Na osi poziomej wykresu znajdują się częstotliwości drgań harmonicznych występujących w badanym dźwięku, na osi pionowej amplitudy tych drgań.

4. Metoda pomiaru

W ćwiczeniu analiza harmoniczna badanych dźwięków dokonywana będzie metodą FFT.

5. Opis stanowiska.

Na stanowisku pomiarowym znajduje się komputer z odpowiednim oprogramowaniem (Visual Analyser). do komputera podłączony jest mikrofon, którego zadaniem jest przetworzenie słyszalnego dźwięku na sygnał elektryczny. oraz źródło dźwięku (gitara).

6. Wyniki pomiaru

pobudzenie najgrubszej struny poprzez szarpnięcie w różnych jej długościach.

długość struny	Częstotliwość [Hz]	Napięcie [volt]
1/2	130,00	15482,10
	260,00	1378,42
	380,00	866,84
1/3	120,00	16157,54
	260,00	5063,45
	380,00	842,50
1/4	120,00	12758,31
	250,00	7742,90
	370,00	899,55

pobudzenie wszystkich strun poczynając od najgrubszej poprzez szarpnięcie w jednakowej długości.

struna	Częstotliwość [Hz]	Napięcie [volt]
I	130,00	22931,67
	250,00	6205,25
	380,00	806,79
II	120,00	25426,72
	230,00	17800,28
	350,00	2002,93
III	160,00	23299,96
	320,00	9870,90
	460,00	8132,77
IV	240,00	10741,69
	500,00	6904,93
	750,00	2630,14
V	260,00	12855,14
	540,00	6899,63
	810,00	589,07
VI	400,00	4010,36
	810,00	1709,60
	1220,00	136,72

pobudzenie najcieńszej struny poprzez szarpnięcie w różnych jej długościach

długość struny [cm]	Częstotliwość [Hz]	Napięcie [volt]
65	400,00	4010,36
	810,00	1709,62
	1220,00	136,72
60	420,00	6328,32
	860,00	865,30
	1290,00	508,29
45	570,00	4627,15
	1150,00	806,23
	1740,00	20,77
30	860,00	6867,34
	1730,00	448,02
	2600,00	175,40

λ= 2L	długość fali stojącej
gdzie L- długość struny
f = 1 / T = ν / λ	Częstość drgań struny
gdzie v - prędkość fali rozchodzącej się w strunie
zatem
	f = v / 2L
	f = v / 2 * 1 / L

L.p.	x=L [m]	y= f [1/s]	1/L
1.	0,65	400	1,538462
2.	0,60	420	1,666667
3.	0,45	570	2,222222
4.	0,30	860	3,333333

Stosując metodę sumy najmniejszych kwadratów otrzymujemy:

a=259,55631 Δa = 4,72029

b= -5,9727 Δb = 10,86538

wsp. worelacji: 0,99967

Prędkość fali w strunie: v = 2a

V= 2 * 259,55631 = 519,11262 [m/s]

Δv= 2 * Δa = 2 * 4,72029 = 9,5 [m/s]

V = 519,1 + 9,5 [m/s]

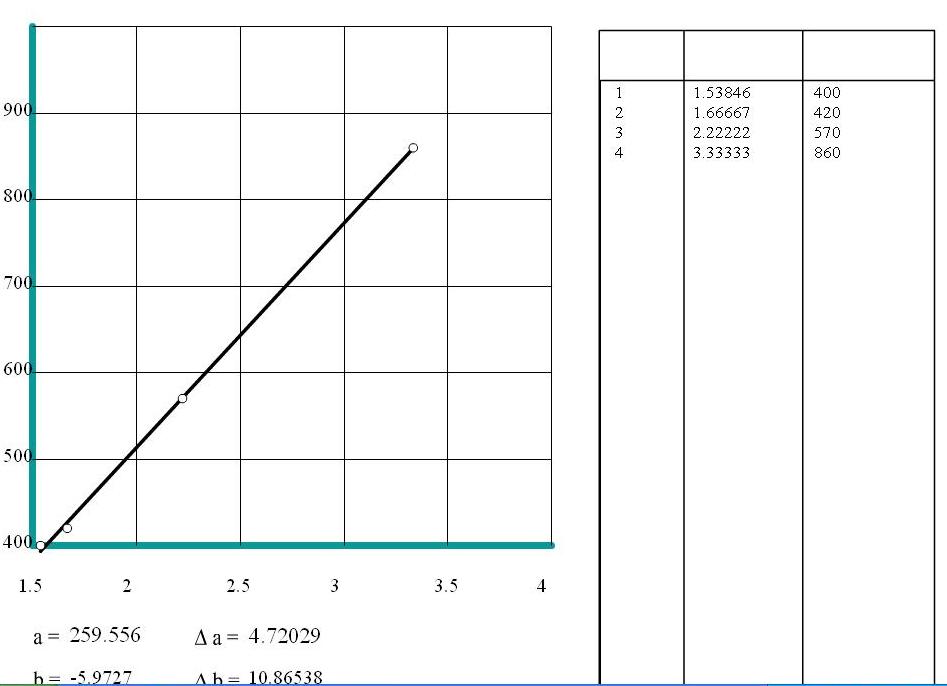
pobudzenie najcieńszej struny poprzez szarpnięcie w różnych jej długościach

Naprężenie	Częstotliwość [Hz]	Napięcie [volt]
maksymalne	140	20239,41
...	120	14203,88
...	110	12647,62
minimalne	80	7122,93

7. Wnioski

Częstotliwości i amplitudy drgań harmonicznych składajacych się na dany dźwięk zależą od cech źródła, a dokładniej od wielkości, kształtu, rodzaju materiału itp.

Z przeprowadzonego badania widzimy, że predkość dźwięku jest zależna od wielu czynników. W przypadku badanych strun zamontowanych w gitarze, jest ich mnóstwo.

Skupiając się na strunie grubej, zaobserwowaliśmy iż widmo dźwiku ulega zmianie gdy struna zostaje pobudzona w innych długościach tej struny.

Podobna zmiana zachodzi gdy zmieniamy naprężenie w strunie. Przy stopniowej zmianie naprężenia struny, widmo jest coraz mniejsze, maleje także prędkość rozchodzenia się dźwięku w strunie.

Porównując widma dźwięków dla wszystkich strun, gdy wzbudzane one były na jednakowych długościach, obserwujemy, iż znaczny wpływ ma budowa przedmiotu (struny), Przy strunie cienkiej (o najmniejszym przekroju) częstotliwość drgań jest o wiele większa niż w przypadku struny grubej...

---