Politechnika Świętokrzyska w Kielcach
Laboratorium elektrotechniki
Ćwiczenie Nr. 3	Temat: Badanie rezonansu napięć i prądów.			Zespół Nr 1 1.Brudnias Damian 2.Swat Kamil 3.Strzygowski Michał
Data wykonania ćwiczenia: 7.11.2005r.		Ocena:	Wydział: WEAiI gr.206B

1. Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie częstotliwości rezonansowej, charakterystyk częstotliwościowych i wykresów wektorowych prądów i napięć w trakcie trwania rezonansu oraz dla częstotliwości różniących się od częstotliwości rezonansowej.

2. Wykaz przyrządów.

- generator z regulowaną częstotliwością

- amperomierze - sztuk 3

- woltomierze - sztuk 3

- płytka z kondensatorem C = 9,3 μF, cewką o indukcyjności L = 330 mH i rezystancją R = 114,6 Ω

- przewody łączeniowe.

3. Schemat pomiarowy:

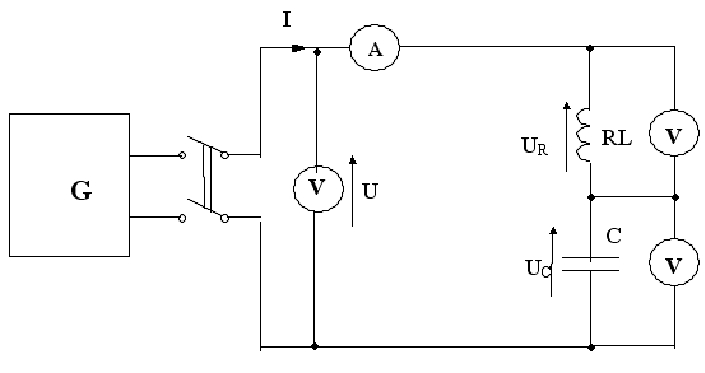
Schemat pomiarowy do badania rezonansu napięć:

Schemat pomiarowy do badania rezonansu prądów:

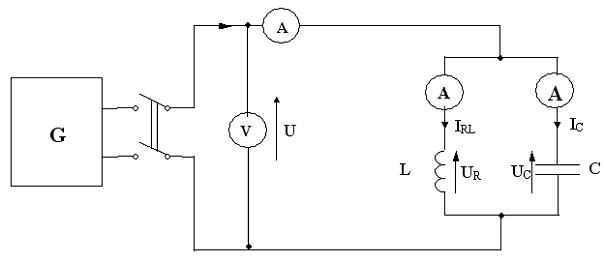
4. Tabele pomiarowe.

Rezonans napięć:

U = 1,5 V R = 114,6 Ω L = 330 mH C = 9,3μF
POMIARY						OBLICZENIA
Lp.	f [Hz]	I[mA]	URL [mV]	UC [mV]	UR [mV]	UL [mV]	|Z| [Ω]	ϕ
1	20	1,2	0,25	1,55
2	30	2,8	0,43	1,68
3	40	4,4	0,7	1,84
4	50	6,5	1,14	2,09
5	60	9,1	1,83	2,41
6	65	10,4	2,23	2,53
7	68	11,0	2,44	2,55
8	69	11,1	2,51	2,53
9	70	11,3	2,58	2,54
10	72	11,5	2,68	2,50
11	75	11,7	2,81	2,43
12	80	11,5	2,89	2,24
13	90	10,3	2,81	1,79
14	100	9,0	2,64	1,44
15	125	6,5	2,24	0,84
16	150	5,0	2,0	0,53
17	200	3,6	1,79	0,3

U = 1,5 V R = 114,6 Ω L = 330 mH C = 9,3μF
	f	ϕ	I	IL	IC	|Z|
Lp.	Hz	°	mA	mA	mA	Ω
1	20		10,1	11,5	1,7
2	30		9,0	10,3	2,7
3	35		8,2	9,7	3,2
4	40		7,5	9,3	3,5
5	50		5,9	8,2	4,5
6	55		5,4	7,9	5,0
7	60		4,7	7,4	5,5
8	65		4,4	7,1	6,1
9	68		4,2	6,8	6,3
10	70		4,1	6,7	6,5
11	71		4,1	6,6	6,6
12	72		4,1	6,5	6,7
13	75		4,0	6,4	7,1
14	80		4,1	6,1	7,5
15	90		4,6	5,6	8,4
16	100		5,3	5,2	9,3
17	125		7,8	4,3	11,5
18	150		10,8	3,7	14,2

5. Przykładowe obliczenia.

REZONANS NAPIĘĆ

Napięcie na rezystancji cewki:

Napięcie na indukcyjności:

Dla f =20 Hz i I= 0,62 mA:

ω = 2⋅π⋅f = 125,66 rad/s

X_L = ω⋅L = 41,47 Ω

Moduł impedancji:

Dla f =20 Hz i I= 0,62 mA:

ω = 2⋅π⋅f = 125,66 rad/s

X_L = ω⋅L = 41,47 Ω

X_C = 1/ωC = 855,7 Ω

R = 114,6 Ω

Kąt ϕ:

Dla f =20 Hz

ω = 2⋅π⋅f = 125,66 rad/s

X_L = ω⋅L = 41,47 Ω

X_C = 1/ωC = 855,7 Ω

R = 114,6 Ω

Częstotliwość rezonansowa obliczona:

Różnica częstotliwości policzonej i zmierzonej:

REZONANS PRĄDÓW

Moduł impedancji:

Dla f =20 Hz

ω = 2⋅π⋅f = 125,66 rad/s

X_L = ω⋅L = 41,47 Ω

X_C = 1/ωC = 855,7 Ω

R = 114,6 Ω

Kąt ϕ:

Przy założeniu, że rezystancja znajduje w gałęzi z cewką wykonujemy następujące obliczeia:

gdzie I_L1 - składowa urojona prądu I_L dla danej chwili

I_L2 - składowa rzeczywista prądu I_L dla danej chwili

I_P - składowa urojona wypadkowa układu dla danej chwili

Obliczanie częstotliwości rezonansowej

Różnica częstotliwości policzonej i zmierzonej:

6. Krzywe rezonansowe I,U_L, U_C, Z w funkcji częstotliwości.

Dla rezonansu napięć:

Dla rezonansu prądów:

7. Wykresy wektorowe.

Dla rezonansu szeregowego:

U_C=U_CMAX

U_C=U_L

U_L=U_LMAX

Dla rezonansu równoległego:

W trakcie rezonansie:

Poniżej częstotliwości rezonansowej (f = 70 Hz):

Powyżej częstotliwości rezonansowej (f = 88 Hz):

8.Wnioski.

Z przeprowadzonych badań i z używanych podczas nich elementów wnioskujemy, że rezonans występuje w obecności elementów LC. Za pomocą obliczeń wyznaczyliśmy częstotliwość rezonansową która różni się od tej uzyskanej w wyniku przeprowadzonych pomiarów. Przypuszczamy, że przyczyną tego było nie uwzględnienie rezystancji i innych pasożytniczych wielkości. Częstotliwość w obwodzie szeregowym i równoległym przy zastosowaniu tych samych elementów jest identyczna, gdyż zależy ona od wartości użytych elementów LC. Przebieg prądu w funkcji częstotliwości dla rezonansu szeregowego charakteryzuje się tym, iż prąd osiąga maksimum przy częstotliwości rezonansowej. Wartości napięć na cewce i kondensatorze, inaczej niż w teorii, mają swe maksima w pobliżu częstotliwości rezonansowej. Jest to spowodowane występowaniem wartości pasożytniczych. Moduł impedancji osiąga swe minimum w funkcji częstotliwości przy f = f rezonansowej. Przy rezonansie prąd ograniczony jest tylko wartością rezystancji i w związku z tym nie jest przesunięty w fazie z napięciem.

Przy rezonansie równoległym prąd osiąga wartość minimalną. Częstotliwość rezonansowa zw teorii zachodzi gdy B_C = B_L, ale w praktyce nie jest tak do końca. Moduł impedancji osiąga maksimum w okolicach częstotliwości rezonansowej. Tak jak w rezonansie szeregowym częstotliwość rezonansowa różni się od tej obliczonej. W czasie zmiany częstotliwości zmieniał się charakter obwodu i kąty między prądami a napięciami zasilającymi. Przy obliczeniach kąta ϕ uwzględniliśmy rezystor połączony w szereg z cewką. W związku na samym początku musieliśmy liczyć przesunięcie między prądem a napięciem w tej gałęzi a potem dopiero całego obwodu wraz z kondensatorem. Dlatego nie skorzystaliśmy ze wzoru na wartość ϕ w połączeniu równoległym R, L, C. Obliczenia nasze mimo, że wykonane w inny sposób są prawidłowe.

---