Piotr Jankowiak gr. C 22. 03. 2000 r.

WM sem. IV ( mgr )

Ćwiczenie nr 20.

Temat: Wyznaczanie stosunku c_p / c_v dla powietrza metodą Clementa i Desoremes'a.

Tabela wyników.

Nr pomiaru	h1 [mmH2O]	h2 [mmH2O]	χ
1	9,2	1,8	1,243
2	10,3	2,2	1,272
3	9,9	2,1	1,269
4	9,7	2,1	1,276
5	10,2	2,3	1,291

χ_śr = 1,2702

W rozumowaniach termodynamicznych często występuje ciepło właściwe przy stałym ciśnieniu c_p oraz ciepło właściwe przy stałej objętości c_v. Stosunek tych dwóch wielkości oznaczamy:

Jest to wykładnik adiabaty, który wynosi:

• dla gazu jednoatomowego χ=1,66

• dla gazu dwuatomowego χ=1,4

• dla gazu wieloatomowego χ=1,3.

Powietrze uważamy jako gaz dwuatomowy ze względu na dwa dominujące w nim atomy: tlenu i azotu. Przyjmujemy także:

• c_p = 5/2 R

• c_v = 3/2 R

• c_p - c_v = R

gdzie R stała gazowa.

Przemiany adiabatyczne są przemianami bez wymiany ciepła z otoczeniem, czyli dq = 0.

Równania POISSONA:

p₁V₁^χ = p₂V₂^χ,

pV^χ = const,

pV = const.

Zasada pomiaru.

W balonie szklanym B o objętości kilkudziesięciu litrów zamknięty jest gaz (powietrze) pod ciśnieniem o p₁ wyższym od ciśnienia atmosferycznego p₃ o około 100 mmH₂O. Na wykresie pV stanowi temu odpowiada punkt 1. Zawór Z pozwala na połączenie balonu z powietrzem atmosferycznym. Otwierając ten zawór na czas około 3 s spowodujemy adiabatyczne rozprężanie gazu. Ciśnienie w butli spada wtedy do ciśnienia atmosferycznego, a więc

Δp_ad = p₁ (1).

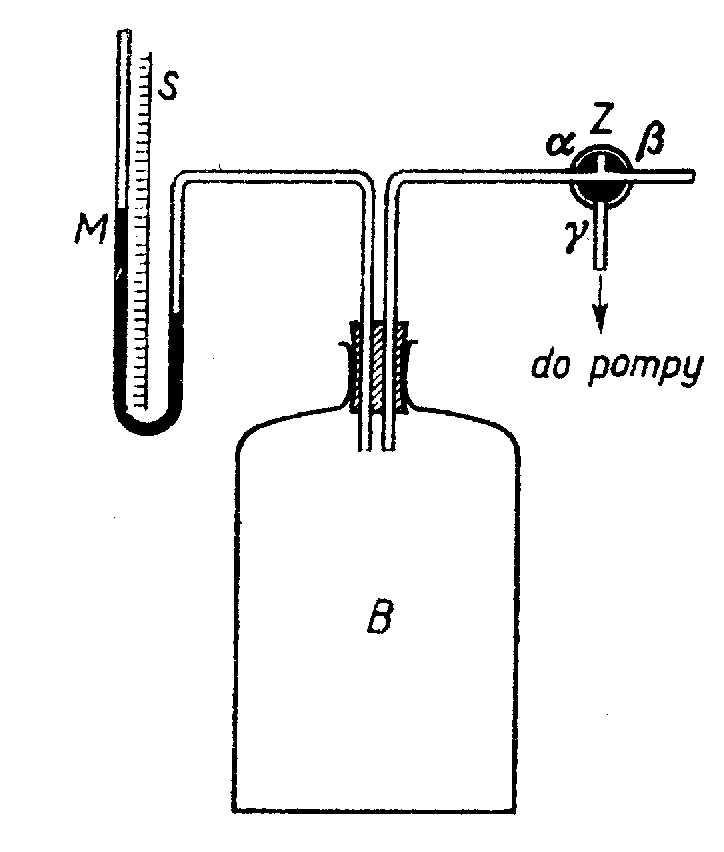
Aparatura do wyznaczania c_p / c_v.

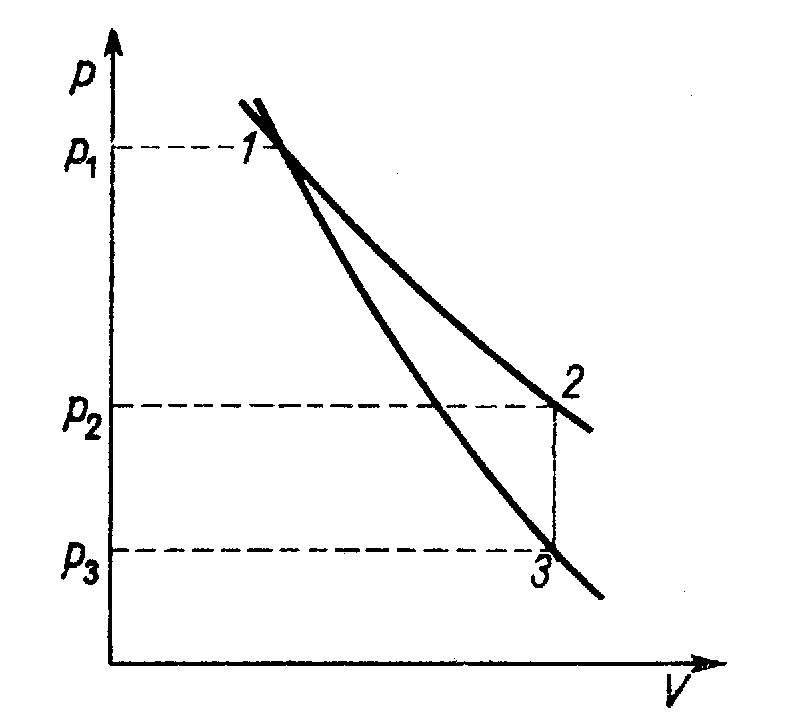
Cykl przemian przy wyznaczaniu χ.

Na wykresie odpowiada to przejściu od punktu 1 do 3 po adiabacie

pV^χ = const (2).

Po zamknięciu zaworu gaz powoli ogrzewa się, a jego ciśnienie wzrasta do wartości p₂ odpowiadającej punktowi 2. Punkty 2 i 3 leżą na tej samej izochorze, ponieważ przemiana odbywa się przy stałej objętości (zamknięta butla). Ze względu na stałość temperatury otoczenia punkty 1 i 2 leżeć muszą na tej samej izotermie

pV = const (3).

Zatem przejściu od punktu 1 do punktu 2 po izotermie odpowiada zmiana ciśnienia

Δp_iz = p₁ - p₂ (4).

Aby znaleźć związek pomiędzy χ a Δp_iz i Δp_ad wykonujemy następujące działania na równaniach (2) i (3).

logarytmowanie

różniczkowanie

przejście do przyrostów skończonych

Dzieląc obydwa równania stronami otrzymamy:

Podstawiając za Δp_ad i Δp_iż wartości z równań (1) i (4) otrzymamy

Ponieważ ciśnienie mierzymy za pomocą manometru wodnego to:

Oszacowanie błędów na podstawie serii pomiarowej.

χ_śr = 1,270

Nr pomiaru	χ	εi	εi^2
1	1,243	0,027	0,000729
2	1,272	-0,002	0,000004
3	1,269	0,001	0,000001
4	1,276	0,006	0,000036
5	1,291	0,021	0,000441

5

---