Spis treści:

Rozdział II: Przykłady projektowania elementów konstrukcji betonowych i żelbetowych

wg PN - B - 03264 - 1999

1. Podstawowe wielkości wytrzymałościowe betonu.

2. Podstawowe wielkości wytrzymałościowe stali zbrojeniowej.

3. Wymiarowanie belek żelbetowych o przekroju prostokątnym ze względu za zginanie.

4. Wymiarowanie belek żelbetowych ze względu na ścinanie.

5. Sprawdzenie szerokości rozwarcia np.

6. Sprawdzenie ugięć belek żelbetowych.

7. Wymiarowanie płyt żelbetowych jednokierunkowo zbrojonych.

8. Wymiarowanie słupów żelbetowych.

9. Wymiarowanie słupów betonowych.

10. Wymiarowanie stropu Akermana.

II.1. Podstawowe wielkości wytrzymałości betonu.

Klasa betonu			B15	B20	B25	B30	B37	B45	B50	B55	B60	B65	B70
Wytrzymałość gwarantowana , MPa			15	20	25	30	37	45	50	55	60	65	70
Wytrzymałość charakterystyczna, MPa		na ściskanie fck	12	16	20	25	30	35	40	45	50	55	60
				na rozciąganie fctk	1,1	1,3	1,5	1,8	2,0	2,2	2,5	2,7	2,9	3,1	3,2
Wytrzymałość średnia na rozciąganie fctm, MPa			1,6	1,9	2,2	2,6	2,9	3,2	3,5	3,8	4,1	4,4	4,5
Wytrzymałość obliczeniowa dla konstrukcji żelbetowych i sprężonych, MPa		na ściskanie fcd	8,0	10,6	13,3	16,7	20,0	23,3	26,7	30,0	33,3	36,7	40,0
				na rozciąganie fctd	0,73	0,87	1,00	1,20	1,33	1,47	1,67	1,80	1,93	2,06	2,13
Wytrzymałość obliczeniowa dla konstrukcji betonowych, MPa	na ściskanie fct		6,7	8,9	11,1	13,9	16,7	19,4	22,2	25,0	27,8	30,6	33,3
Moduł sprężystości			26	27,5	29	30,5	32	33,5	35	36	37	38	39

II.2. Podstawowe wielkości wytrzymałości stali zbrojeniowej.

Klasa stali	Gatunek	Średnica prętów [mm]	Granica plastyczności		Wytrzymałość charakterystyczna ffk [MPa]
							charakterystyczna fyk [MPa]	obliczeniowa fyd [MPa]
A-0	St0S	5,5 - 40	220	190	260
A-I	St3SX, St3SY	5,5 - 40	240	210	310
A-II	18G2	6 - 32	355	310	410
A-III	34GS	6 - 32	410	350	500
A-III N	20G1VY	6 - 28	490	420	500

Moduł sprężystości E_s=

II.3. Wymiarowanie belek żelbetowych o przekroju prostokątnym
ze względu na zginanie.

1. Wymagania dotyczące zbrojenia belek.
   

1. 
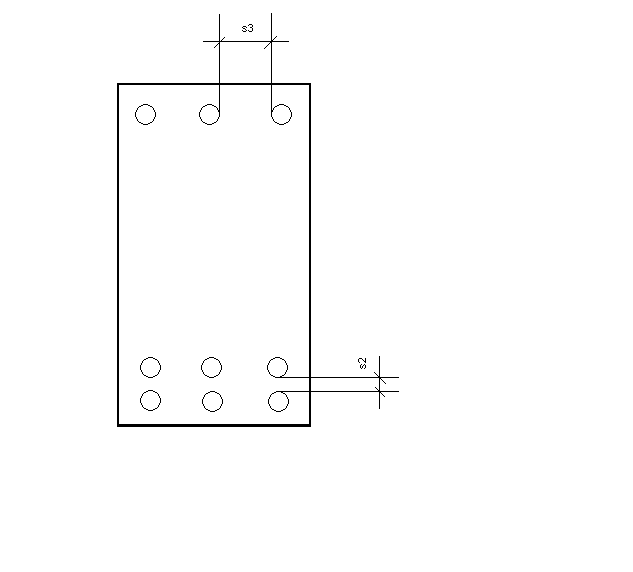
   minimalny rozstaw prętów.

dg - maksymalny wymiar kruszywa

2. średnica podłużnych rozciąganych prętów
   ,

3. średnica podłużnych prętów ściskanych
   ,

4. co najmniej
   zbrojenia potrzebnego w przęśle musi być doprowadzona do podpory bez odgięć, ale nie mniej niż 2 pręty,

5. średnica strzemion w elementach monolitycznych
   , ale nie więcej niż 12mm, powinna stanowić co najmniej 0,2 średnicy zbrojenia podłużnego,

6. w belkach o szerokości
   można stosować strzemiona pojedyncze,
   

7. 
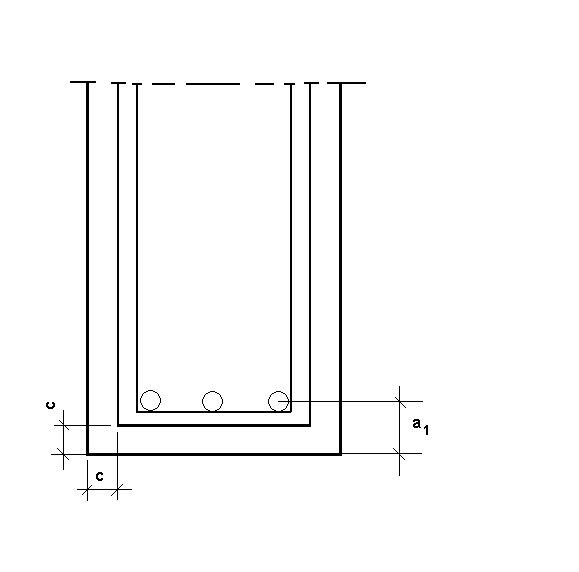
   otulina (a₁)

+ ø_s +
ø

ø_s - średnica strzemiona

ø - średnica prętów nośnych

a₁ - otulina

c - otulina (zależy od klasy środowiska)

Przy projektowaniu belek minimalna grubość otuliny powinna być zwiększona o odchyłkę Δh (zależy od poziomu wykonawstwa i kontroli jakości).

Dla elementów wykonywanych na placu budowy Δh = 5-10mm. Ze względu na p. poż. otulenia mogą być jeszcze większe.

1. Ogólne zasady sprawdzania stanu granicznego nośności zgięciowej.

Polega na wykazaniu, ze w każdym przekroju belki moment zginający wywołany obciążeniem obliczeniowym jest mniejszy lub równy maksymalnemu momentowi wywołanemu działaniem sił wewnętrznych.

Powstające w elemencie siły wewnętrzne doprowadzają do powstania stanu granicznego nośności gdy:

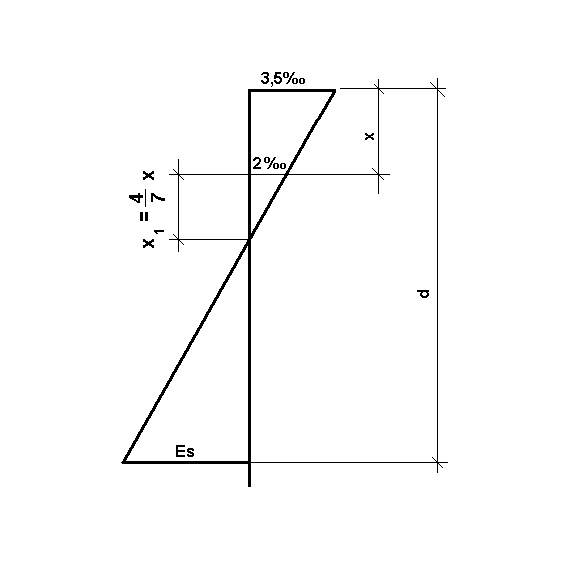
1. odkształcenie w stali rozciąganej osiągnie
   ‰

2. odkształcenie w skrajnym ściskanym włóknie betonu będzie równe
   = 3,5‰

W celu wyznaczenia sił wewnętrznych przyjmuje się następujące założenia:

1. wytrzymałość betonu na rozciąganie jest pomijana,

2. naprężenia w strefie ściskanej mają wykres prostokątny

Są dwa modele obliczeniowe:

A Zależność między naprężeniami a odkształceniami ma postać

w [‰]

B model uproszczony (wymaga spełnienia warunków sił uogólnionych).

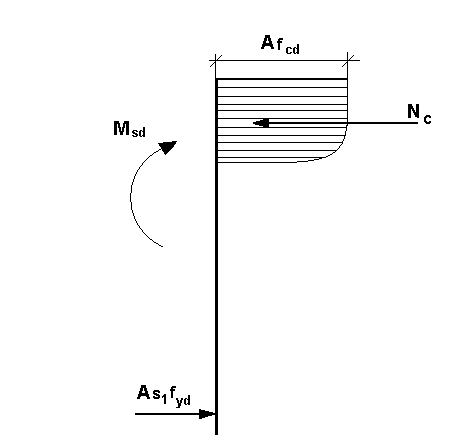
f_cd - wytrzymałość obliczeniowa betonu na ściskanie
(w konstrukcjach żelbetowych)

f_yd - wytrzymałość obliczeniowa stali

Krzywoliniowa zależność
na odcinku
, na pozostałych
naprężenia są stałe
i wynoszą

Niewiadomymi są:

x - wysokość strefy ściskanej

As₁ - powierzchnia stali zbrojeniowej

Można je znaleźć korzystając z warunków:

1 warunek równowagi sił:

2 warunek równowagi momentów:

W celu znalezienia powierzchni zbrojenia As₁ wylicza się zasięg strefy ściskanej
z równania 2 i podstawia do 1. Kończy to obliczenia ale musi być spełniony warunek odkształcenia w stali
<10‰. Doprowadza to do tego, że względna wysokość strefy ściskanej x musi spełniać warunki:

i

Należy zwrócić uwagę na stopień zbrojenia

- minimalny stopień zbrojenia (zależy od klasy stali i betonu) [%]

beton stal	B15	B20	B25	B30	B37	B45	B50
A-0	0,75	0,99	1,25	1,56	1,88	2,18	2,51
A-I	0,68	0,90	1,13	1,42	1,70	1,98	2,27
A-II	0,46	0,61	0,76	0,96	1,15	1,34	1,54
A-III	0,41	0,54	0,68	0,85	1,02	1,19	1,36

- maksymalny stopień zbrojenia

beton stal	B15	B20	B25	B30	B37	B45	B50
A-0	2,28	3,02	3,79	4,76	5,70	6,64	7,61
A-I	2,02	2,68	3,35	4,21	5,04	5,87	6,73
A-II	1,23	1,63	2,05	2,57	3,08	3,59	4,11
A-III	1,05	1,39	1,79	2,19	2,62	3,06	3,50

Stopień zbrojenia
oblicza się ze wzoru:

Można oszacować maksymalną wartość momentu, który może przenieść przekrój pojedynczo zbrojony.

Stal
A-0	0,95	0,7865	0,4284
A-I	1,05	0,7692	0,4235
A-II	1,55	0,6931	0,993
A-III	1,75	0,6667	0,3900

S_c,max - moment statyczny pola betonu strefy ściskanej względem środka
ciężkości zbrojenia rozciąganego

Proporcje wyników belek prostokątnych

Podstawowy wpływ na wymiary przekroju mają wymagania stanów granicznych:

1. ugięcie

2. zginanie

3. ścinanie

4. zaupowanie

ad a) Przy ustalaniu wstępnych wymiarów przekroju korzysta się z warunku na stan graniczny ugięcia. Jeżeli z obliczeń wychodzi, że
to decydujące znaczenie o wymiarach przekroju ma zginanie. W tej sytuacji należy założyć proporcje
i ponownie obliczyć
b i d z zależności
.

ad c) Przy silnie obciążonych belkach, o małej rozpiętości należy sprawdzić, czy dobrze są dobrane wymiary przekroju ze względu na duże ścinanie.

Wymiary muszą spełniać warunek.

ad d) W większości typowych przypadków stan graniczny zarysowania nie ma wpływu na wymiary przekroju. Gdy dopuszczalna szerokość rozwarcia np. W_lim=0,1 mm to należy liczyć się z tym, że o wymiarach przekroju decyduje stan graniczny zarysowania. Dlatego wymiary przekroju należy zwiększyć: b-0 30% z h-40% w stosunku do wymiarów wynikających ze stanu granicznego zginania belki.

1. Wymiarowanie belki o przekroju prostokątnym za pomocą równań.

Algorytm postępowania:

1.Przyjęcie betonu i stali, założenie stopnia zbrojenia.

2.Wstępne ustalenie wymiarów przekroju ze względu na stan graniczny ugięcia.

l_eff - rozpiętość obliczeniową

3.Obliczenie potrzebnego pola przekroju zbrojenia As₁ korzystając
z modelu A lub modelu B.

Przykład 1. Belka swobodnie podparta o rozpiętości w świetle podpór 6m, obciążona równomiernie na całej długości obciążeniem q_o (bez ciężaru własnego belki). Zaprojektować belkę jeżeli q_o = 20 kN/m.

1. Przyjęto beton B 25, stal A-III

dla B 25 f_cd = 13,3 MPa,

dla A-III f_yd = 350 MPa

2. Założono stopień zbrojenia

3. Obliczenie rozpiętości obliczeniowej.

4. Obliczanie momentu maksymalnego.

Obciążenie q_o należy zwiększyć o ciężar własny belki, który stanowi 5 - 10% całego obciążenia. My przyjmujemy 10% i zwiększamy obciążenie mnożąc je przez 1,1.

5. Z tabeli do wymiarowania przekrojów zginanych odczytano parametr główny A dla

A = 3,51 MPa

Korzystając ze wzoru pomocniczego
można obliczyć b.

6. Obliczenie wysokości użytecznej przekroju ”d” z warunku na stan graniczny ugięcia.

7. Obliczenie szerokości belki „b”

8. Na tej podstawie przyjęto

wysokość belki

przyjęto otuliny a₁ = 4cm
+
ø =

ostatecznie dla ujednolicenia przyjęto h = 45cm

szerokość belki b = 20cm

wysokość użyteczna przekroju d = h-4 = 45-4 = 41cm

9. Obliczenie potrzebnego zbrojenia As₁ dla modelu A

(równanie kwadratowe)

Z równania równowagi sił otrzymuje się

pole przekroju zbrojenia

Przyjęto 4Ø18 o As₁ = 10,18 cm²

rzeczywisty stopień zbrojenia

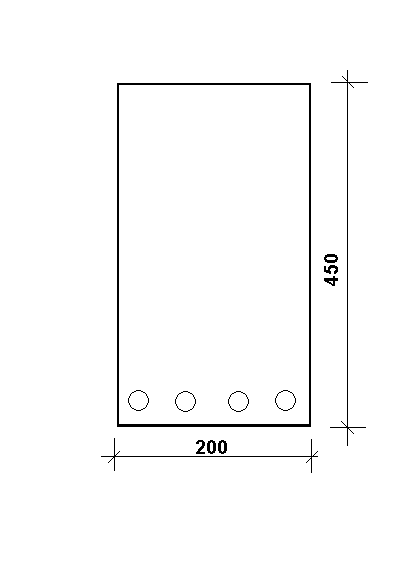
Należy przyjmować jak najwięcej prętów o małych średnicach (nie odwrotnie), ale tak żeby można je było umieścić w jednym szeregu, w przeciwnym wypadku zmieni się „d” i obliczenia należy zacząć od nowa. Należy pamiętać o zachowaniu odległości między prętami zgodnie z zaleceniami normy.

Dla porównania obliczamy zbrojenie dla modelu B.

(równanie kwadratowe)

Wyniki w obu przypadkach są prawie identyczne.

Wymiarowanie belek żelbetowych o przekroju prostokątnych przy pomocy tablic.

Algorytm postępowania:

1. Przyjęcie zbrojenia betonu, stopnie zbrojenia.

2. Wstępne ustalenie wymiarów przekroju poprzecznego ze względu na stan graniczny ugięcia.

3. Ustalenie zbrojenia nośnego na podstawie tablic 1

• wyliczamy główny parametr „A” ze wzoru

• z tabeli 1 dla danego betonu i stali i obliczonego „A” odczytujemy
  ‰

• dla obliczonego „A” odczytujemy stopień zbrojenia
  i obliczamy potrzebne zbrojenie ze wzoru:

Przykład 1. Zaprojektować przy pomocy tablic belkę żelbetową swobodnie podpartą o przekroju prostokątnym. Belka obciążona jest obciążeniem ciągłym równomiernie rozłożonym o wartości q_o=45kN/m (bez ciężaru własnego), rozpiętość belki w świetle podpór l_n=5,5m.

1. Przyjęto.

beton B 30 f_cd = 16,7 MPa

stal A-III f_yd = 350 MPa

2. Założono stopień zbrojenia
.

3. Rozpiętość obliczeniowa.

4. Moment maksymalny

5. Wstępne przyjęcie wymiarów przekroju.

dla
, stali A-III i betonu B 30 z tabeli odczytujemy główny parametr A = 3,83 MPa

założono proporcje wymiarów przekroju do wzoru

za d wstawiamy 2b

Przyjęto b=0,25m, h=0,50m, d=0,5 - 0,04=0,46m

6. Obliczenie zbrojenia nośnego z wykorzystaniem tablic

Tablice 1 służą do wymiarowania na podstawie modelu A.

Oblicza się
i dla danego betonu i stali

1. odczytuje się
   ‰

2. odczytuje się stopień zbrojenia
   i oblicza się powierzchnię zbrojenia ze wzoru:

• obliczamy parametr główny „A”

• dla betonu B30 i stali A-III z tablic odczytano (po interpolacji)

‰ < 10‰

• obliczamy zbrojenie nośne

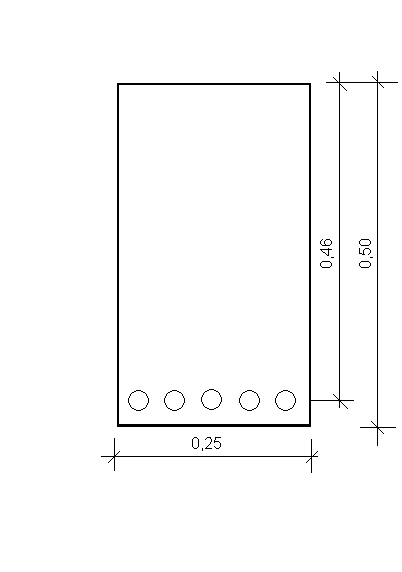
przyjęto 5Ø20 A_s1=15,71cm²

Na podstawie tablic można znaleźć nośność belki o przekroju prostokątnym.

Przykład. Znaleźć nośność belki o przekroju prostokątnym b=0,30m, h=0,50m, d=0,46cm. Belka wykonana z betonu B20 i stali A-II. Zbrojenie nośne składa się z 6 prętów Ø18.

1. dla 6Ø18 A_s1=15,27cm²=0,001527m²

2. stopień zbrojenia belki

3. dla
   z tablic odczytano A=2,758MPa

4. Moment maksymalny obliczamy ze wzoru:

Odp. Nośność belki wynosi M_max=0,175MNm

II.4. Wymiarowanie belek żelbetowych ze względu na ścinanie.

Metoda kratownicowa

o zmiennym kącie

nachylenia krzyżulców

betonowych.

Algorytm postępowania:

1. Obliczenie siły tnącej V_sd miarodajnej (w licu podpory)

2. Obliczenie V_Rd1, jest to siła, która powoduje takie naprężenia rozciągające, które jest w stanie przenieść sam beton.

Jeżeli

V_sd < V_Rd1

to nie liczymy zbrojenia na ścinanie, jedynie w strefie przypodporowej
(to jest na długości
) należy zagęścić strzemiona, czyli rozstaw ich nie może być większy niż

s_max

3. Jeżeli V_sd > V_Rd1 to należy wymiarować przekrój ze względu na ścinanie

k - współczynnik określający efekt stali

1,0 - jeżeli do podpory doprowadzono mniej niż 50% prętów

1,6 - d d w [m]

f_ctd - wytrzymałość obliczeniowa betonu na rozciąganie

- stopień zbrojenia prętów podłużnych (bez prętów odgiętych)

Możliwe są dwa rozwiązania:

• siłę ścinającą przenoszą same strzemiona

• siłę ścinającą pręty odgięte i strzemiona

4. Liczymy długość strefy przypodporowej na której potrzebne jest zbrojenie na ścinanie (l_t)

q_o - całkowite obciążenie z ciężarem własnym belki

1. jeżeli
   

to oznacza, że wpływ ścinania na nośność belki jest niewielki. W takim przypadku siłę

ścinającą przenoszą same strzemiona.

Ze wzoru na „V_Rd3” (siła w krzyżulcu rozciąganym bez prętów odgiętych)

przyjmujemy

obliczamy potrzebny rozstaw strzemion „s₁”

A_sw1 - pole przekroju poprzecznego prętów tworzących jedno strzemię

strzemiona dwuramienne A_sw1=2a_w1

(a - pole przekroju pręta z którego wykonano strzemię)

f_ywd1 - granica plastyczności strzemion

z - ramię sił wewnętrznych w przekroju

Obliczony rozstaw strzemion musi spełniać wymagania normy.

Z formalnego punktu widzenia należy sprawdzić warunek:

- współczynnik f_ck w [MPa]

2. jeżeli l_t > 2d

to oprócz strzemion trzeba zaprojektować pręty odgięte.

Długość l_t dzieli się na odcinki, które obejmują poszczególne pręty odgięte (l_t1, l_t2, l_t3...).

Przy wymiarowaniu bierze się do obliczeń maksymalną siłę tnącą dla każdego odcinka (patrz przykład). Na odcinkach gdzie uwzględnia się pręt odgięty wartość kąta
wynika z geometrii przekroju i rozstawu prętów.

Obliczenia przeprowadza się w następujący sposób:

• ustala się odcinki l_t1, l_t2, l_t3...

• dla każdego oblicza się miarodajną siłę tnąca (jest to siła poprzeczna maksymalna na tym odcinku)

• ustala się rozstaw odgięć s₂

• oblicza się siłę przenoszoną przez pręt odgięty na danym odcinku, ze wzoru:

A_sw2 - pole przekroju poprzecznego prętów odgiętych

α - kąt nachylenia prętów odgiętych

- kąt nachylenia „krzyżulca betonowego”, musi być spełniony warunek:

• ustala się wartość siły przenoszonej przez strzemiona (V_w1), musi być spełniony warunek:
  

• oblicza się rozstaw strzemion na danym odcinku ze wzoru:

• sprawdza się nośność krzyżulców betonowych, musi być spełniony warunek:

V_Rd2 - graniczna siła poprzeczna ze względu na ukośne ścinanie, oblicza się ze wzoru:

- współczynnik obliczony ze wzoru
f_ck w [MPa]

Jeżeli warunek nie jest spełniony należy zmienić (zwiększyć) wymiary przekroju belki
i obliczenia zaczynać od początku.

Zalecenia praktyczne dotyczące obliczeń ze względu na ścinanie:

1. Jeżeli rozstaw strzemion z obliczeń wychodzi za duży (nie spełnia zaleceń normy) to najprostszym rozwiązaniem jest zmniejszenie
   ich średnicy np. z Ø8 na Ø6.

2. Gdy rozstaw jest mniejszy niż 50 mm to należy zwiększyć średnicę strzemion (zbyt gęsto ułożone strzemiona utrudniają betonowanie).

3. Praktycznym rozwiązaniem jest ujednolicenie rozstawu strzemion na danym odcinku l_t - do najmniejszego z obliczonych s₁. Kosztem niewielkiego wzrostu zużycia stali ułatwia się i przyśpiesza konstruowanie szkieletu zbrojeniowego i eliminuje możliwość popełnienia błędów.

4. Średnica strzemion w belkach monolitycznych od 4,5 ÷ 12 mm, ze stali klasy A - 0, A - I.

5. Rozstaw strzemion zależy od
   

- jeżeli
to

- jeżeli
to

- jeżeli
to

- jeżeli
i szerokość belki >300mm to należy stosować strzemiona czteroramienne.

6. Rozstaw prętów odgiętych w strefie przypodporowej.

7. Pręty zbrojenia dolnego mogą być odginane aby przy podporze przenieść siły tnące lub momenty ujemne. Nie należy bez potrzeby odginać prętów zbrojeniowych, komplikuje to wykonawstwo, a korzyści są ograniczone ponieważ strzemiona zawsze muszą przenieść siłę równą co najmniej 50% siły tnącej. Praktycznie wystarcza odgięcie jednego pręta a w przypadku dużych sił tnących (gdy l_t > 5d) dwóch prętów.

Przykład. Zaprojektować belkę żelbetową ze względu na zginanie i ścinanie. Belka o przekroju prostokątnym, obciążona obciążeniem ciągłym równomiernie rozłożonym o wartości
(bez ciężaru własnego). Rozpiętość belki w świetle podpór 5,6 m (l_n=5,6 m).

1. Przyjęto beto B 25 f_cd = 13,3MPa, f_ck = 20 MPa, f_ctd = 1,0 MPa

pręty nośne stal A-III f_yd = 350 MPa

strzemiona stal A-0 f_ywd1 = 210 MPa

Wymiarowanie ze względu na zginanie.

2. Założono stopień zbrojenia

3. Rozpiętość obliczeniowa belki.

4. Moment maksymalny od obciążeń obliczeniowych.

5. Wstępne przyjęcie wymiarów przekroju.

dla
, A-III, B 25 z tablic odczytano

dlatego założono, że

przyjęto b = 0,25 m, h = 0,55 m, d = 0,55-0,4 = 0,51 m

6. Obliczenie zbrojenia głównego ze względu na zginanie.

a)

b) dla B 25 i A-III z tablic odczytano:

= 3,23‰ < 10‰

c) przekrój zbrojenia nośnego ze względu na zginanie

przyjęto 5Ø22 o A_s1 = 19 cm²

rzeczywisty stopień zbrojenia

Wymiarowanie ze względu na ścinanie.

1. Obliczenie siły poprzecznej miarodajnej (w licu podpory)

reakcje

miarodajna siła tnąca w licu podpory

2. Obliczenie siły przenoszonej przez sam beton.

• zakładamy, że do podpory doprowadzimy bez odgięć 3Ø22 o Q_s = 11,4 cm²

• współczynnik k = 1,6 - d = 1,6 - 0,51 = 1,09 m

(dlatego że do podpory doprowadzono > niż 50% prętów bez odgięć)

3. Długość odcinka, na którym potrzebne jest zbrojenie ze względu na ścinanie.

l_t > 2d

dlatego należy zastosować pręty odgięte

Odcinek l_t podzielono na 3 części

l_t1 = 0,52 m

l_t2 = 0,57 m

l_t3 = 0,36 m - na tym odcinku tylko same strzemiona

4. Wymiarowanie zbrojenia na odcinku pierwszym l_t1 = 0,52 m

• miarodajna siła tnąca w licu podpory

• rozstaw odgięć s₂ = l_t2 = 0,57 m

• dla prętów Ø22 pole powierzchni pojedynczego pręta
  

• siła przenoszona przez pręt odgięty

• ponieważ V_w2 = 161 kN > 0,5V_sd = 78,54 kN to strzemiona należy zaprojektować

na siłę V_w1 = 0,5V_sd

V_w1 = 78,54 kN = 0,07854 MN

• przyjęto strzemiona Ø8 dwuramienne ze stali A-I o f_ywd1 = 210 MPa i przekroju
  

• obliczamy rozstaw strzemion na odcinku l_t1

• potrzebna liczba strzemion na tym odcinku

• sprawdzenie nośności krzyżulców betonowych (V_WR2)

nośność nie jest przekroczona

• ponieważ

to rozstaw strzemion na odcinku l_t1 musi być mniejszy niż

warunek jest spełniony dlatego, że s₁ = 0,139m = 139 mm

5. Odcinka l_t2 nie wymiarujemy dlatego, że ma on nośność prawie taką samą jak odcinek l_t2,
a miarodajna siła tnąca jest dużo mniejsza od siły na odcinku l_t2.

na odcinku l_t1 V_sd = 157,08 kN

na odcinku

6. Wymiarowanie zbrojenia na odcinku l_t3 = 0,36 m

siłę tnącą przeniosą same strzemiona

• 
  

• miarodajna siła tnąca na tym odcinku

• ponieważ
  długość odcinka l_t3 musimy zwiększyć tak żeby
  

czyli

• obliczamy rozstaw strzemion na tym odcinku

l_t3 = 0,46 m,

• przyjęcie rozstawu strzemion 0,076m na odcinku l_t3 oznaczałoby różny rozstaw

strzemion w strefie przypodporowej (dlatego, że na odcinku l_t1 i l_t2 s₁ = 0,139m). W celu ujednolicenia i ułatwienia wykonawstwa przedłużamy dodatkowo odcinek l_t3 do
Na tym odcinku rozstaw strzemion będzie wynosił:

7. Ostatecznie przyjęto na całym odcinku przypodporowym:

rozstaw strzemion s₁ = 0,135m

na odcinku l_t = 2,01m należy zastosować 16 strzemion Ø 8 co 0,135m (13,5 cm)

II.5. Sprawdzenie szerokości rozwarcia rys.

Obliczanie szerokości rozwarcia rys jest pracochłonne. W wielu wypadkach nie ma potrzeby wykonywania pracochłonnych szczegółowych obliczeń.

Najczęściej sprawdzenie szerokości rozwarcia rys polega na porównaniu średnic użytego w projekcie zbrojenia nośnego z maksymalnymi wartościami średnic podanymi w tabeli.

Obliczenia należy przeprowadzić gdy:

1. Ø > Ø_max

2. zawsze gdy dopuszczalna szerokość rys W_lim = 0,1mm

Z tabeli można korzystać jeżeli:

1. 
   

2. zbrojenie w belce zostało prawidłowo zaprojektowane ze względu na zginanie

Maksymalne średnice prętów zbrojenia, przy których spełniony jest stan graniczny szerokości rozwarcia rys.

Stopień zbrojenia	KLASA STALI
		A - I		A - II		A - III		A - IV
		Wlim = 0,2	Wlim = 0,3	Wlim = 0,2	Wlim = 0,3	Wlim = 0,2	Wlim = 0,3	Wlim = 0,2	Wlim = 0,3
1,00	18	32	18	32	14	31	8	22
1,50	27	32	27	32	20	40	12	23
2,00	32	32	32	32	28	40	16	28

Przykład. Do zadania z obliczenia zbrojenia na ścinanie, sprawdzić czy zachowany jest stan graniczny rozwarcia rys.

• belka żelbetowa w środowisku suchym, wewnątrz budynku: klasa środowiska - 1

• graniczna wartość szerokości rozwarcia rys dla kl. 1 W_lim = 0,3

• 
  można skorzystać z tabeli

• dla stopnia zbrojenia
  , dla klasy stali A - III, przy W_lim = 0,3 z tabeli

odczytano maksymalna średnicę zbrojenia, przy której spełniony jest stan graniczny

szerokości rozwarcia rys.

Ø_max = 40mm

zastosowano zbrojenie Ø = 22mm

czyli Ø22 < Ø 40

Warunek szerokości rozwarcia rys jest zachowany.

II.6. Sprawdzenie ugięć belek żelbetowych.

Sprawdzenie stanu granicznego ugięć polega na wykazaniu, że ugięcie obliczone jest mniejsze niż wartość graniczna dopuszczalna dla danego typu konstrukcji.

Dokładne obliczanie ugięć jest bardzo pracochłonne, a konieczne tylko w wyjątkowych przypadkach (przy belkach słabo obciążonych o dużych rozpiętościach). Dlatego wygodnie jest korzystać z uproszczonych zależności umożliwiających szybkie szacowanie ugięć. Do tego celu służy tabela.

Maksymalna wartość
przy których stan graniczny ugięcia nie jest przekroczony.

A - I			A - II			A - III
[%]	B15	B25	[%]	B15	B25	[%]	B15	B25
1,00	29,7	30,7	1,00	20,1	20,8	1,00	17,8	18,4
1,25	26,7	28,6	1,25	18,7	19,4	1,25	16,5	17,1
1,50	25,8	26,8	1,50	17,4	18,2	1,50	15,4	16,1

Tabela ta została opracowana dla belek swobodnie podpartych przy założeniu:

,
Ø

q_d - obciążenie długotrwałe

q - obciążenie całkowite

- średni współczynnik obciążenia

Ø
- współczynnik pełzania

Jeżeli belki mają inne rozpiętości to:

a)
- współczynnik z tablicy należy pomnożyć przez 0,8

b)
- współczynnik z tablicy należy pomnożyć przez (1 - 0,133)

Przykład. Do zadania na obliczanie ścinania

l_eff = 5,88 m, b = 0,25 m, h = 0,55 m, d = 0,51m, Ø
= 2,

• maksymalna wartość
  z tabeli
  (po interpolacji)

• wartość rzeczywista
  

• wniosek
  

Ugięcia nie są przekroczone.

II.7. Wymiarowanie płyt żelbetowych jednokierunkowo zbrojonych.

1. Zalecenia konstrukcyjne.

1. grubość płyty monolitycznej nie może być mniejsza niż:

• płyty stropowe w obiektach budownictwa powszechnego - 60 mm

• płyty dachowe - 50 mm

2. średnica zbrojenia nośnego:

• w płytach monolitycznych - Ø ≤ 4,5 mm

• w płytach prefabrykowanych (zbrojonych siatką zgrzewaną) - Ø ≤ 3 mm

3. odstęp między prętami zbrojenia głównego „a”

• 
  przy płytach o grubości h_ff > 100 mm

• gdy h_ff ≤ 100 mm, a ≤ 120 mm

• praktycznie nie stosuje się rozstawów a < 50 mm

4. zbrojenie rozdzielcze nie powinno mieć rozstawu większego niż 300 mm, a nośność nie mniejszą niż
   zbrojenia głównego na mb przy obciążeniu równomiernie rozłożonym i
   nośności zbrojenia głównego przy siłach skupionych.

5. otulina zbrojenia płyty w każdym przypadku co najmniej 15 mm, ale nie mniej niż średnica zbrojenia

6. stopień zbrojenia w typowych rozwiązaniach
   

2. Algorytm postępowania.

1. Wstępne przyjęcie wymiarów płyty

musi być spełniony warunek:

d - wysokość użyteczna przekroju

l_eff - rozpiętość obliczeniowa płyty

Ø

Ø - średnica pręta nośnego

c - otulenie

2. Wymiarowanie płyty ze względu na zginanie.

Wymiaruje się jak belkę o szerokości b = 100 cm i wysokości h_f. Ustala się średnicę prętów nośnych i odstępy między nimi.

3. Sprawdzenie nośności ze względu na ścinanie.

Nośność płyty na ścinanie nie decyduje o jej grubości, należy jednaj sprawdzić dla płyty o d Ø ≤ 4h_f.

Nośność na ścinanie nie jest przekroczona jeżeli:

V_sd ≤ V_Rd1

V_sd ≤ V_Rd2

b_w = 1 m

- wytrzymałość betonu na ścinanie

Przykład. Zaprojektować płytę żelbetowa jednokierunkowo zbrojoną wg danych:

1. obciążenie (razem z płytą) przypadające na 1 m².

płyty q₀ = 9,3 kN/m²

na pas o szerokości 1 m

2. rozpiętość w świetle podpór l_n = 2,5m

3. przyjęto stal A-I f_yd = 210 MPa

beton B20 f_cd = 10,6 MPa

1. Rozpiętość obliczeniowa.

2. Moment maksymalny.

3. Moment maksymalny.

Ø

założono wstępnie grubość płyty h_ff = 0,09m

założono pręty o śr. Ø = 10mm

otulenie c = 1,5 cm

4. Sprawdzenie warunku sztywności.

5. Obliczanie potrzebnego zbrojenia przypadającego na 1 m szerokości płyty.

1. obliczanie głównego parametru

z tabeli 2 odczytujemy stopień zbrojenia

Jeżeli odczytany stopień zbrojenia będzie mniejszy niż 1,2%, to należy zmniejszyć grubość płyty. Jeżeli stopień zbrojenia będzie większy niż 1,2% to należy zwiększyć grubość płyty.

z tabeli 2 odczytujemy ξ_eff = 0,205 < ξ_eff,lim = 0,62

2. obliczanie zbrojenia głównego

• przyjęto zbrojenie Ø8 o a_s1 = 0,50 cm²

• rozstaw prętów można oszacować w sposób przybliżony korzystając z tabeli,

przyjmując dla Ø 8 rozstaw osiowy 8 cm i wtedy pole przekroju na 1 m płyty będzie wynosić A_s1 = 6,29cm²

wtedy rzeczywisty stopień zbrojenia

• rozstaw prętów można obliczyć w następujący sposób

należy przyjąć a = 0,08 m

rzeczywiste pole zbrojenia

i wtedy rzeczywisty stopień zbrojenia

6. Sprawdzenie nośności ze względu na ścinanie:

V_sd ≤ V_Rd1

V_sd ≤ V_Rd2

1. miarodajna siła tnąca

V_sd = 11,62kN < V_Rd1 = 51 kN

warunek jest spełniony

V_sd = 11,62 kN < V_Rd2 = 207 kN

warunek jest spełniony

II.8. Wymiarowanie słupów żelbetowych.

1. Zalecenia konstrukcyjne.

1. Minimalny przekrój słupa 0,25 x 0,25 m.

Gdy stopień zbrojenia jest niewiele większy od minimalnego wymiary przekroju można zmniejszyć do 0,20 x 0,20 m.

2. Norma zaleca, żeby smukłość słupów nie przekraczała
   , l_o - długość obliczeniowa

3. Zbrojenie główne słupów wykonuje się z prętów o średnicach od Ø 12 do Ø 32 ze wskazaniem na większe średnice.

4. W każdym narożu musi być co najmniej jeden pręt.

5. 
   Minimalny stopień zbrojenia musi spełniać warunek

N_sd - siła podłużna wywołana obciążeniem obliczeniowym

6. Maksymalny stopień zbrojenia

bez istotnej potrzeby nie należy zwiększać ponad 3%

7. Rozstaw prętów głównych
   

8. Strzemiona:

• minimalna średnica 4,5 mm lecz nie mniej niż 0,2Ø prętów głównych

• rozstaw strzemion:

gdy
- 15Ø zbrojenia głównego

gdy
- 10Ø zbrojenia głównego

minimalne z

2. Wiadomości ogólne.

Słupy żelbetowe są zwane mimośrodowo ściskanymi, dlatego, że siła podłużna działająca w osi słupa uważana jest za siłę prawie osiową. Wynika to z tego, że idealne osiowo przyłożenie siły jest w praktyce niemożliwe. W tych warunkach powstaje mimośród niezamierzony (przypadkowy) oznaczony symbolem „e_a”, którego wartość należy przyjmować następująco:

Jeżeli siła działa w pewnej odległości od osi , to wartość mimośrodu konstrukcyjnego „e_e” oblicza się z wzoru:

Całkowity mimośród (mimośród początkowy) „e₀”

e₀ = e_a + e_e

Jeżeli musi się uwzględnić wpływ smukłości i obciążeń długotrwałych to mimośród początkowy należy zwiększyć mnożąc go przez współczynnik „
”.

współczynnik
oblicza się ze wzoru:

N_crit - siła krytyczna

Konieczność uwzględnienia wpływu smukłości i obciążeń długotrwałych występuje gdy:

l₀ - długość obliczeniowa

Wartość siły krytycznej oblicza się ze wzoru:

J_c - moment bezwładności przekroju betonowego liczony względem środka ciężkości przekroju

J_c - moment bezwładności stali zbrojeniowej liczony względem środka ciężkości przekroju betonowego

k_lt - współczynnik uwzględniający wpływ obciążenia długotrwałego

Ø_(∞,to)

N_sd,lt - siła długotrwała

Ø_(∞,to) - współczynnik pełzania, gdy brak szczegółowych danych, Ø_(∞,to) = 2

- musi spełniać warunek:

f_cd - w [MPa]

E_cm - średnia wartość E_c,nom

Praktycznym problemem jest wyznaczenie siły krytycznej gdy nieznana jest dokładna ilość zbrojenia. Najczęściej szacuje się J_s na podstawie zakładanych (przy określaniu wymiarów) stopni zbrojenia
i
.

Gdy po zwymiarowaniu przekroju okaże się, że sumaryczna powierzchnia zbrojenia różni się od założonej o ponad 20% to należy powtórzyć całe wymiarowanie od obliczenia N_crit dla powierzchni zbrojenia będącej średnią z uprzednio założonej i otrzymanej w wyniku wymiarowania.

Przekrój poprzeczny słupa żelbetowego.

A_s1 - zbrojenie w strefie rozciąganej (lub mniej ściskanej)

A_s2 - zbrojenie w strefie ściskanej

e_s2 - odległość między osią działania siły a osią zbrojenia A_s2,

e_s1 - odległość między osią działania siły N_sd a osią zbrojenia A_s1,

gdy należy uwzględnić wpływ smukłości to za e_e podstawić e_tot
X_eff - wysokość ściskanej

3. Wstępne przyjmowanie wymiarów przekroju słupa.

Ze względu na sposób projektowania rozróżnia się następujące rodzaje słupów:

1. betonowe

2. żelbetowe

3. uzwojone

ad. a) Słupy betonowe.

Słupy te mają przekrój kwadratowy. Wymiar boku przekroju można oszacować z zależności:

- wytrzymałość obliczeniowa dla konstrukcji betonowych

Jeżeli słup jest bardzo smukły tzn.
to wymiary można nieco zwiększyć. Ostatecznie wymiary zaokrągla się do pełnych 5 cm, gdy bok jest > 60 cm to do 10 cm.

ad. b) Słupy żelbetowe.

Na sposób przyjmowania wymiarów podstawowy wpływ ma wielkość mimośrodu.

1) Mały mimośród (cały przekrój jest ściskany, ale liczymy się z występowaniem strefy rozciąganej)

O wymiarach przekroju decyduje wielkość siły i przekrój jest zbliżony do kwadratu.

Algorytm postępowania:

• zakłada się sumaryczny stopień zbrojenia
  
  

• zakładając proporcje boków np.
  z zależności obliczamy wymiary przekroju.

lub

Mimośród jest na tyle mały, że cały przekrój słupa będzie ściskany, to o wymiarach przekroju decyduje wartość siły N_sd. Wymiary można przyjąć z warunku:

przy założeniu, że b i h różnią się niewiele

Sumaryczny stopień zbrojenia musi być większy minimalnego.

2) Duży mimośród.

Jeżeli strefa rozciągana występuje w przekroju słupa i ma duży zasięg, to o wymiarach przekroju decyduje wartość momentu zginającego. Przekrój ma kształt prostokątny o proporcjach belki zginanej.

Algorytm postępowania:

• zakładamy stopień zbrojenia
  np.
  

• z tablic dla belek zginanych odczytuje się odpowiadającą mu wartość „A”

• zakładamy proporcję boków
  , z zależności
  odczytujemy wymiary słupa

• stopień zbrojenia ściskanego
  można oszacować z warunku:

4. Wymiarowanie słupów z dużym mimośrodem.

przyjmuje się
,
- odczytujemy z tabeli

lub

Zbrojenie w strefie ściskanej

Zbrojenie w strefie rozciąganej

Graniczna wartość

Klasa stali
A - 0	0,63
A - I	0,62
A - II	0,55
A - III	0,53

Jeżeli A_s2 jest ujemne lub mniejsze od
to oznacza, że przekrój słupa jest za duży. Jeżeli nie można go zmniejszyć to A_s2 przyjąć konstrukcyjnie i przy obliczaniu A_s1 założyć A_s2 = 0

5. Wymiarowanie słupów z małym mimośrodem.

Zbrojenie oblicza się ze wzoru:

• zbrojenie w strefie ściskanej

• zbrojenie w strefie rozciąganej

Jeżeli A_s2 jest ujemne lub mniejsze d minimalnego należy zmniejszyć przekrój lub przyjąć:

Jeżeli A_s1 jest ujemne, to należy spróbować zwymiarować jak dla dużego mimośrodu.

• Powinno się sprawdzić stopień zbrojenia wykorzystanej stali
  , wtedy jest 100% wykorzystanie stali

,
- z równania

Przykład. Zaprojektować słup żelbetowy obciążony siłą N_sd=2500kN = 2,5MN na mimośrodzie e_e=0,03m. Słup w jednokondygnacyjnym budynku halowym, utwierdzony w stopie fundamentowej i połączony z konstrukcją dachu w sposób przegubowy. budynek bez suwnic, przykryty dachem o konstrukcji sztywnej.

,

wysokość słupa l_cd=3,5m,

długość działania siły N_sd,lt = 1900kN

Przyjęto:

beton B 25,
;

stal A - II f_yd = 310 MPa

1. Wstępne przyjęcie wymiarów przekroju

przyjęto wstępnie h = 45 cm = 0,45 m i b = 40 cm = 0,4 m

a₁ = a₂ = 0,04m

2. Sprawdzenie smukłości słupa

• długość obliczeniowa
  

należy uwzględnić wpływ wyboczenia

3. Obliczanie mimośrodu całkowitego

1. mimośród przypadkowy

przyjęto e_a=1,5cm = 0,015m

2. mimośród początkowy

3. obliczanie współczynnika zwiększającego mimośród początkowy

• siła krytyczna

moment bezwładności stali - założono stopień zbrojenia

dla B 25

przyjęto

Ø =

mimośród całkowity

4. sprawdzenie czy w przekroju jest strefa rozciągana

to siła znajdująca się w rdzeniu przekroju (nie ma strefy rozciąganej)

Cały przekrój jest ściskany. Wymiarujemy jak dla małego mimośrodu.

4. Obliczanie zbrojenia ściskanego

5. Obliczanie zbrojenia w strefie mniej ściskanej

należy sprawdzić czy ten stopień zbrojenia jest mniejszy od minimalnego

przyjęto

W strefie rozciąganej przyjęto zbrojenie A_s1=A_s1,min

6. Sumaryczny stopień zbrojenia.

Założony stopień zbrojenia to 2,5%, ponieważ 20% z 2,5% to 0,5%. Można uznać, że zbrojenie zaprojektowano prawidłowo.

7. Przyjęto:

• w strefie ściskanej 4Ø25 o A_s2 = 19,64 cm²

• w strefie mniej ściskanej 3Ø25 o A_s1 = 14,73 cm²

• rzeczywisty stopień zbrojenia
  

8. Uwagi praktyczne

1. Jeżeli A_s2 > 0 natomiast A_s1 < 0 to albo przyjmujemy
   , albo liczymy jeszcze raz jak dla dużego mimośrodu.

2. Jeżeli A_s2 < 0 lub mniejsze od minimalnego to należy zmniejszyć wymiary przekroju.

II.9. Wymiarowanie słupów betonowych.

Słupy betonowe to takie słupy, w których w ogóle nie użyto stali zbrojeniowej lub stopień zbrojenia jest mniejszy od minimalnego.

Nośność słupa betonowego sprawdza się ze wzoru:

- uwzględnia smukłość i pełzanie betonu, zależy od
a jego wartość podana jest w tabeli w normie

e_o - w słupach betonowych jest to tylko mimośród początkowy przyjmowany jako:

l_cd - odległość między podporami

- wytrzymałość obliczeniowa betonu dla konstrukcji betonowych

l_eff - zastępcza długość obliczeniowa obliczona ze wzoru:

l₀ - obliczeniowa długość słupa

k_lt - współczynnik

Ø_(∞,to)

N_sd,lt, N_sd, Ø_(∞,to) - jak w słupach żelbetowych

Wpływ smukłości i pełzania uwzględnia się gdy

h - wysokość przekroju słupa

W przeciwnym wypadku przyjmuje się l_eff = l₀

Algorytm postępowania przy projektowaniu słupów z betonu klasy nie wyższej niż B 20:

1. ustala się długość obliczeniową i zastępczą

2. wstępnie przyjmuje się wartość współczynnika
   (najczęściej
   

3. ze wzoru
   oblicza się wymiary słupa przyjmując b = h i po zaokrągleniu oblicza się wartość współczynnika
   

4. sprawdza się nośność słupa

5. jeżeli nośność słupa jest za duża lub za mała przeprowadza się korektę wymiarów

Gdy słup jest projektowany z betonu klasy wyższej niż B 20 to jego nośność określa się zgodnie z zasadami podanymi dla słupów żelbetowych, przyjmując w odpowiednich wzorach A_s1 = A_s2 = 0 i
.

Przykład. Zaprojektować słup betonowy obciążony osiowo siłą obliczeniową N_sd = 850 kN (0,85 MN). Długotrwała część obciążenia N_sd,lt = 650kN.

Długość obliczeniowa słupa l₀ = 3,5 m.

Przyjęto beton B 15 o

1. Ustalenie zastępczej długości obliczeniowej.

Ø_(∞,to) =

2. Wstępnie przyjęto
.

3. Obliczenie wymiarów przekroju ze wzoru.

założono przekrój kwadratowy b = h

przyjęto wymiary słupa 45 x 45 cm

4. Mimośród niezmierzony (początkowy).

5. Ustalenie wartości współczynnika.

z tabeli odczytano

6. Sprawdzenie nośności

850 MN < 1060 kN

Nośność jest za duża. Można spróbować sprawdzić nośność dla słupa o przekroju 40 x 40 cm.

7. Zakładamy wymiary 40 x 40 [cm].

• 
  mimośród początkowy

• 
  ustalenie wartości współczynnika
  

z tabeli odczytano

• sprawdzenie nośności

nośność jest przekroczona

Ostatecznie przyjęto 45 x 45 [cm]

II.10. Wymiarowanie stropu Akermana.

Przykład. Zaprojektować zbrojenie nośne stropu Akermana, o rozpiętości w świetle ścian l_n=4,70 m. Strop pracuje jako swobodnie podparty. Na wykonanie stropu przewidziana beton B 20 i stal A - III. Przyjęto strop z pustaków o wysokości 20 cm z nadbetonem 4 cm. Na stropie znajdują się pomieszczenia biurowe.

1. Zestawienie obciążeń na 1 m² stropu.

Rodzaj obciążenia	qk		q
1. Obciążenia stałe:
a) deszczułki podłogowe na lepiku 22 mm	0,23	1,1	0,253
b) gładź cementowa 10 mm	0,19	1,3	0,247
c) podkład betonowy 40 mm	0,92	1,3	1,196
d) papa 1 warstwa	0,05	1,2	0,06
e) styropian 30 mm	0,013	1,2	0,016
f) warstwa wyrównawcza 20 mm	0,38	1,3	0,494
g) ciężar własny stropu (z tabeli)	3,13	1,1	3,44
h) tynk cementowo - wapienny 15 mm	0,285	1,3	0,371
	5,198		6,577
2. Obciążenie zmienne:
pomieszczenia biurowe	2,0	1,3	2,6
	7,198		9,177

Obciążenie obliczeniowe przypadające na 1 m² stropu:

2. Na jedno żebro przypada.

3. Rozpiętość obliczeniowa.

4. Schemat statyczny.

5. Moment maksymalny.

6. Przekrój obliczeniowy żebra.

przyjmujemy a₁ = 30 mm = 0,03m

d = 240 - 30 = 210 mm = 0,21m

Przyjęto przekrój pozornie teowy o wymiarach:

b_eff x h = 0,31 x 0,24 [m]

7. Obliczanie zbrojenia nośnego żebra.

dla B 20 i stali A-III stopień zbrojenia
,

przyjęto Ø14 o

8. Sprawdzenie ze względu na ścinanie.

maksymalna siła tnąca

Nie ma potrzeby sprawdzania ze względu na ścinanie gdy spełniony jest warunek:

za b podstawiamy b = 0,07m

k = 1,6 - d = 1,39

Obliczanie zbrojenia na siły tnące jest zbędne.

9. Sprawdzenie szerokości rozwarcia rys.

stopień zbrojenia

z tabeli odczytano Ø_max przy której stan graniczny szerokości rozwarcia rys nie jest przekroczony dla A-III i
Ø_max = 31 mm

Ø14 < Ø31

stan graniczny rozwarcia rys nie jest przekroczony

10. Sprawdzenie ugięcia.

Do sprawdzenia ugięcia stopień zbrojenia liczymy w ten sposób, że za b podstawiamy b_eff.

dla betonu B 20, stali A-III i
z tabeli odczytano
przy którym ugięcia nie są przekroczone:

rzeczywista wartość

Ugięcia nie są przekroczone.

- 6 -

ø

20mm

dg + 5mm

1,5 ø

30mm

dg + 5mm

0,5 ø

10mm

1,5 ø

30mm

dg + 5mm

k

50 mm

h

na tych odcinkach siłę tnącą przeniosą pręty odgięte i strzemiona

300 mm

a ≤

1,5 h

250 mm

słup ściskany osiowo słup ściskany mimośrodowo

e_e - mimośród konstrukcyjny

e_e = max

l_cd - odległość między podporami [cm]

h - wysokość przekroju

M_sd - maksymalny moment
na długości słupa

N_sd - siła ściskająca obliczeniowa

β - współczynnik uwzględniający pracę słupa, sposób zamocowania końców (z normy)

E_s - moduł sprężystości stali

E_s = 210000 MPa

e_e = max

CD

---