AGH Metrologia Laboratorium					Grupa: Rafał Sopliński Paweł Straszak Rafał Szemraj Marcin Szydełko
^wydział EAIiE	^rok akademicki 2001/2002		^rok studiów II
Temat : Badanie własności dynamicznych przetworników pomiarowych i korekcja dynamiczna.
^data wykonani^a 11.10.2001		^data zaliczenia 16.10.2001		^ocena

1. Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z modelami przetworników pomiarowych, ich podstawowymi cechami i właściwościami.

2. Część teoretyczna:

Ponieważ elektryczne sygnały pomiarowe są często pochodnymi badanych lub mierzonych sygnałów innego typu (np.: akustycznych lub mechanicznych) toteż informacje o mierzonej wielkości mogą być zakodowane w każdym z parametrów elektrycznego sygnału przetwarzanego przez dany układ pomiarowego przetwornika (np. w amplitudzie, częstotliwości, fazie, szerokości impulsów). Z tego względu różnorodność tych układów jest bardzo duża i zalicza się do nich między innymi: filtry, wzmacniacze pomiarowe, czujniki czy przekładniki.

3. Pomiary i wyznaczanie charakterystyk:

1. Pomiary rozpoczęliśmy od zmontowania układu pomiarowego wykorzystując dostępny układ przetwornika pomiarowego stopnia I-go oraz zestaw mierników (woltomierze cyfrowe i oscyloskop).

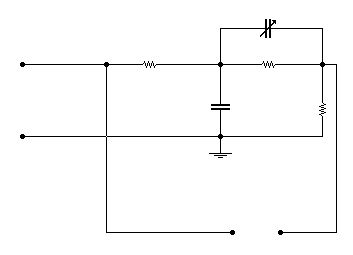
2. Następnym krokiem było odpowiednie dobranie wartości kondensatora jako jednego z elementów układu korektora. Celem tej operacji było otrzymanie na wyjściu układu przebiegu jak najbardziej zbliżonego kształtem do sygnału podawanego na wejście. Zmieniając dekadowo wartość pojemności jednocześnie obserwowaliśmy i porównywaliśmy na ekranie oscyloskopu kształty obu przebiegów. Oceniliśmy, że przebiegi najbardziej były zbliżone do siebie dla wartości C = 0,11 μF. Dla tej wartości nie następował również efekt przesterowania sygnału wyjściowego.

3. Kolejnym etapem było wyznaczenie stałej czasowej dla trzech poszczególnych części obwodu:

• Układu inercyjnego z korektorem;

• Układu inercyjnego bez korektora;

• Samego korektora.

Jeżeli na wejście danego układu podamy sygnał skokowy (np. przebieg prostokątny) to sygnał na wyjściu jako odpowiedź na to wymuszenie będzie miał postać funkcji czasu
, gdzie C jest stałą charakterystyczną dla przebiegu wejściowego i związaną z jego amplitudą a τ - stałą czasową danego obwodu. Widzimy, że po czasie t = τ równanie to przyjmuje postać
. Znajdując więc przedział czasu, po którym amplituda sygnału wyjściowego stanowi 0,637 amplitudy sygnału wymuszenia znajdujemy stałą czasową danego układu. Stałą czasową możemy również wyznaczyć metodą graficzną znajdując punkt przecięcia się stycznej do krzywej propagacji w punkcie (0,0) z krzywą y = C, czyli wartością amplitudy po czasie ustalania.

Wyniki pomiarów dla poszczególnych układów:

• Układ inercyjny z korekcją:

U_wy ustalone = 4,5 [V] 0,637*U_wy = 2,86 [V]

τ₁ = 1,4 [ms]

• Układ inercyjny bez korekcji

U_wy ustalone = 7,2 [V] 0,637*U_wy = 4,58 [V]

τ₂ = 4,4 [ms]

• Układ samego korektora

U_wy ustalone = 6,0 [V] 0,637*U_wy = 3,82 [V]

τ₃ = 1,2 [ms]

4. Kolejnym etapem pomiarów było wyznaczenia charakterystyk amplitudowej i fazowej każdego z trzech układów. Pod spodem umieszczamy wyniki pomiarów w postaci tabel pomiarowych i wykresów
   i
   (wykresy zależności amplitudy sygnału wyjściowego i przesunięcia fazowego mięedzysygnałowego w zależności od częstotliwości sygnału podawanego na wejście).

• Układ inercyjny z korektorem:

Dla U_we = 7 V

f [Hz]	Uwy [V]	Δϕ [rad]
10	1,4	0,00
100	1,22	10,05
250	0,84	91,06
500	0,51	138,16
750	0,35	160,14
1000	0,23	125,60
1500	0,16	113,04
2000	0,12	1,38
3000	0,08	17,33
5000	0,05	21,35
6000	0,04	12,81

Szukamy częstotliwości granicznej tego układu:

Z definicji wynika, że częstotliwość graniczna to taka przy której wzmocnienie maleje o 3 dB. Z takiego założenia wynika, że
. Dla naszego napięcia wejściowego Uwe = 7 V ⇒ Uwy=4,9. Z wykresu i tabeli wynika więc, że częstotliwość graniczna tego układu leży dużo poniżej 10 Hz.

Pogrubiona linia przedstawia teoretyczną charakterystykę fazowo-częstotliwościową.

UWAGA: Wyniki w zakreślonej części tabeli (dotyczące wartości przesunięć fazowych) są obarczone dużym błędem spowodowanym faktem odczytywania wartości generowanej częstotliwości bezpośrednio z pokrętła generatora, które prawdopodobnie było źle skalibrowane (wskazywało inną częstotliwość niż rzeczywiście generowana). Bardziej właściwym postępowaniem w tej sytuacji było by sprawdzanie wartości częstotliwości sygnału wejściowego na ekranie oscyloskopu.

• 
  
  Układ korektora:

Dla U_we = 7 V

f [Hz]	Uwy [V]	Δϕ [^o]
10	6,91	14
100	2,18	60
250	1,01	85
500	0,54	78
750	0,36	75
1000	0,23	85
1500	0,16	102
2000	0,12	103
3000	0,09	85
5000	0,05	89
6000	0,04	94

Szukamy częstotliwości granicznej tego układu:

Dla naszego napięcia wejściowego Uwe = 7 V ⇒ Uwy=4,9.

Pogrubiona linia przedstawia teoretyczną charakterystykę fazowo-częstotliwościową.

UWAGA: Wyniki w zakreślonej części tabeli (dotyczące wartości przesunięć fazowych) są obarczone dużym błędem spowodowanym faktem odczytywania wartości generowanej częstotliwości bezpośrednio z pokrętła generatora, które prawdopodobnie było źle skalibrowane (wskazywało inną częstotliwość niż rzeczywiście generowana). Bardziej właściwym postępowaniem w tej sytuacji było by sprawdzanie wartości częstotliwości sygnału wejściowego na ekranie oscyloskopu.

Wnioski :

1. Układ z korektorem ma dużo mniejsza stałą czasową niż układ bez korektora. Wniosek z tego taki, że zastosowanie układu korektora powoduje, że cały układ nie wprowadza znacznych zniekształceń sygnału (kształt bardziej zbliżony do wejściowego).

2. Na podstawie charakterystyki napięciowo-częstotliwościowej wnioskujemy, że dany układ jest filtrem dolnoprzepustowym, czyli przenosi sygnały małej częstotliwości (dany układ do ok. 10 Hz). Sygnały wysokich częstotliwości są zwierane przez kondensator C do masy.

3. Dzięki zastosowaniu w układzie korektora kondensatora nastawnego możemy poprzez regulację doprowadzić do sytuacji w której cały układ wprowadza tylko niewielkie znieksztalcenia kształtu sygnału.

4. Badany przez nas układ jest układem I-go rzędu, czyli takim którego sygnał wyjściowy nie oscyluje w czasie ustalania.

Charakterystyki wyznaczone na podstawie symulacji komputerowej wykonanej za pomocą programu Workbench.

Układ z korektorem

f [Hz]	Uwy [V]	Δϕ [^o]
10	1,37	4
25	1,36	7
50	1,33	14
75	1,28	21
100	1,23	25
125	1,16	31
150	1,11	35
175	1,07	39
200	0,97	44
300	0,76	55
400	0,62	64
600	0,43	71
800	0,33	74
1000	0,27	79

Układ samego korektora

f [Hz]	Uwy [V]	Δϕ [^o]
5	1,4	-4
10	1,44	-11
25	1,64	-25
50	2,17	-38
75	2,79	-40
100	3,38	-43
125	3,9	-40
150	4,3	-38
175	4,7	-38
200	5	-36
300	5,8	-32
400	6,5	-29

Układ inercyjny bez korektora

f [Hz]	Uwy [V]	Δϕ [^o]
5	6,94	7
10	6,78	16
25	5,92	30
50	4,35	50
75	3,27	62
100	2,58	68
125	2,12	74
150	1,79	75
175	1,54	73
200	1,36	75
300	0,92	82
400	0,69	80
600	0,46	86

1

5

T

y(t)= A(1-e^-1)

Elementy układu korektora

t [ms]

y(t)

y(t)=A

C

---