   

 

Wydział Mechaniczny

Laboratorium Kinematyki, Dynamiki i Teorii Drgań

Ćwiczenie nr 5.2.1 i 5.2.2

Temat: Doświadczalne wyznaczanie momentów bezwładności metodą ruchu obrotowego oraz metodą wahadła fizycznego

Semestr: V Skład grupy:

Studia: dzienne Paweł Frankowski

Studium magisterskie Tomasz Jagła

Grupa: A Robert Gugała

Zespół: III Ireneusz Olszak

Rok akademicki: 1999/2000 Adam Sagan

1.METODA RUCHU ODROTOWEGO

1. Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z metodą doświadczalną wyznaczania momentów bezwładności. Metodą tą jest metoda ruchu obrotowego. Doświadczalne wyznaczanie masowych momentów bezwładności brył jest istotne ze względu na często występujące trudności z analitycznym ich określeniem.

W ćwiczeniu wyznaczamy masowe momenty bezwładności brył metodą ruchu obrotowego drogą doświadczalną i porównamy z wynikami analitycznymi.

2. 
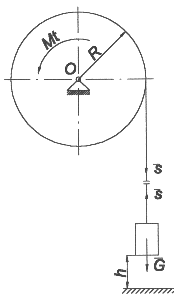
   Schemat stanowiska badawczego oraz badanego koła zębatego i krążka:
   
   

Szkic stanowiska badawczego

Uproszczony rysunek koła zębatego badanego w ćwiczeniu

Rysunek krążka badanego w ćwiczeniu

3. Część teoretyczna:

Punktem wyjścia w metodzie ruchu obrotowego jest Druga Zasada Dynamiki Newtona dla ruchu obrotowego, którą zapisać możemy:

Badane ciało porusza się ruchem obrotowym opisanym równaniem:

I₀ = SR - M_t

gdzie:

 - Przyspieszenie kątowe ruchu obrotowego

S - napięcie w linie

M_t - moment tarcia

Ciężarek porusza się ruchem postępowym opisanym równaniem:

gdzie: p - przyspieszenie ciężarka

Jeżeli uwzględnimy, że:

p = R

oraz założymy, że ruch ciężarka jest jednostajny, to:

po powiązaniu ze sobą powyższych równań i wyrugowaniu S otrzymujemy:

Uwzględniając warunki przeprowadzania badania ostatni wzór zapisać możemy w postaci:

gdzie:

G₁ - masa pierwszego ciężarka w N

G₂ - masa drugiego ciężarka w N

h - droga jaką przebywają ciężarki w m

t₁ - czas ruchu pierwszego ciężarka w s

t₂ - czas ruchu drugiego ciężarka w s

R - promień krążka na który nawijano nić

Wyznaczanie momentów bezwładności

Dla stanowiska

gdzie R = 0,035m

Dla stanowiska wraz z krążkiem

Dla stanowiska wraz z kołem zębatym

Analiza błędów.

W analizie błędów przyjmuję (dla uproszczenia), że błędy popełnione zostały w pomiarach wykonanych przez studentów - czyli przy pomiarze wielkości: h, t₁, t₂.

Błąd bezwzględny masowego momentu bezwładności wynosi:

gdzie:

błąd względny pomiaru wynosi:

Podstawiając otrzymane wyniki do powyższych wzorów otrzymujemy:

Dla stanowiska:

Błędy bezwzględne pomiaru drogi h i pomiaru czasu t ustalam odpowiednio:

h = 0,002m

t₁ = t₂ = 0,02s

ostatecznie błąd bezwzględny masowego momentu bezwładności stanowiska wynosi:

I₀ = 0,0000035591514 Ns²m

błąd względny dla stanowiska wynosi:

Ostatecznie moment bezwładności dla stanowiska z uwzględnieniem błędu wynosi:

I₀ = 0,00000643819050,0000035591514 kgm²

Przy błędzie względnym wynoszącym 55,28 % dla ustalonych przeze mnie błędów bezwzględnych przyrządów pomiarowych.

Dla stanowiska wraz z krążkiem:

Wzory na I_0, a_1, a₂, a₃ są identyczne jak przy obliczeniach momentu bezwładności samego stanowiska. Po podstawieniu odpowiednich wartości otrzymujemy:

a₁ = - 0,00106302257 Ns²

a₂ = 0,00232902344 mNs

a₃ = - 0,00118919556 mNs

I₀ = 0,0000523443844 Ns²m

Błąd względny pomiaru dla układu stanowisko + krążek wynosi:

∂_  5,150116804 %

Ostatecznie moment bezwładności dla stanowiska wraz z krążkiem z uwzględnieniem błędu wynosi:

I₀ = 0,0010163727610,0000523443844 Ns²m

Przy błędzie względnym wynoszącym 5,15 % dla ustalonych przeze mnie błędów bezwzględnych przyrządów pomiarowych.

Dla stanowiska wraz z kołem zębatym:

Wzory na I_0, a_1, a₂, a₃ są identyczne jak przy obliczeniach błędu dla momentu bezwładności samego stanowiska. Po podstawieniu odpowiednich wartości otrzymujemy:

a₁ = -0,00755757269 Ns²

a₂ = 0,01624559281 mNs

a₃ = -0,01183825600 mNs

I₀ = 0,0004023107059 Ns²m

Błąd względny pomiaru dla układu stanowisko + koło zębate wynosi:

∂_  5,378037601 %

Ostatecznie moment bezwładności dla stanowiska wraz z kołem zębatym z uwzględnieniem błędu wynosi:

I₀ = 0,0074806227796 ± 0,0004023107059 Ns²m

Przy błędzie względnym wynoszącym 5,38 % dla ustalonych przeze mnie błędów bezwzględnych przyrządów pomiarowych.

Analityczne wyznaczenie momentu bezwładności

Wyprowadzenie wzoru na moment bezwładności dla rury

Analitycznie wyznaczam moment bezwładności dla krążka z otworem o średnicy r = 0,0075 m, średnicy zewnętrznej R = 0,048 m i masie m = 2,205 kg

Wnioski, komentarze i omówienie wyników:

Na podstawie analizy otrzymanych wyników stwierdzić można, że metoda doświadczalna obarczona jest dosyć dużym błędem wynoszącym dla stanowiska 55,28 %, natomiast błąd przy wyznaczaniu masowego momentu bezwładności dla krążka i dla koła zębatego był mniejszy i wynosił odpowiednio 5,15 % i 5,38 %. Błędy te wynikały z dokładności przeprowadzonego badania. Największy wpływ na powstanie błędów miał pomiar czasu, a ściślej rzecz biorąc refleks mierzącego oraz ustawienie odważników na podanej wysokości - talerzyk był przekrzywiony i stąd duża zmienność ustawienia. Duży wpływ na dokładność pomiarów mają także takie czynniki jak: drgania talerzyka z odważnikami, tarcie występujące nie tylko pomiędzy linką a krążkiem, ale również w ułożyskowaniu wałka na którym był osadzony badany przedmiot ( to wszystko wpływało na zakłócenie ruchu obrotowego)- czynniki te nie zostały uwzględnione w obliczeniach momentu bezwładności co mogło mieć znaczący wpływ na rozbieżność pomiędzy momentem bezwładności wyznaczonym doświadczalnie a momentem wyznaczonym analitycznie. Metody analityczne nie uwzględniają powyższych czynników, jednak w wielu przypadkach teoretyczne wyznaczenie momentów bezwładności może być bardzo skomplikowane ( np. koło zębate) lub wręcz niemożliwe. Dokładność metody doświadczalnej można zwiększyć poprzez zastosowanie nowoczesnej techniki pomiarowej.

2. METODA WAHADŁA FIZYCZNEGO

1. Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z metodą doświadczalną wyznaczania momentów bezwładności. Metodą tą jest metoda wahadła fizycznego. Doświadczalne wyznaczanie masowych momentów bezwładności brył jest istotne ze względu na często występujące trudności z analitycznym ich określeniem.

W ćwiczeniu wyznaczamy masowe momenty bezwładności brył metodą wahadła fizycznego drogą doświadczalną i porównamy z wynikami analitycznymi.

2. Schemat układu:

1 - trzpień; 2 - ciężarek; 3 - nakrętki; 4 - badana bryła

Metoda wahadła fizycznego polega na tym, że badaną bryłę zawieszamy na osi przechodzącej przez jej środek.

Ciężar P ważymy zgodnie z poniższym schematem:

l

P

Q_w

e_w

Rysunki badanych brył

Rysunek krążka badanego w ćwiczeniu

Uproszczony rysunek koła zębatego badanego w ćwiczeniu

3. Równania wykorzystane w obliczeniach:

- wzór na moment bezwładności na drodze doświadczalnej:

• dla krążka:

• dla koła zębatego:

- wzór na moment bezwładności dla metody analitycznej dla krążka (wyprowadzenie wzoru znajduje się w części poświęconej wyznaczaniu momentów bezwładności metodą ruchu obrotowego na str. 10):

I₀ = 0,5m(R² - r²)

- wzory na wyznaczenie błędów:

bezwzględnego na drodze doświadczalnej:

względnego:

4. Obliczenia:

Moment bezwładności z doświadczenia:

dla :

L = 0,432 m

P = 0,73575 N

T_W = 1,222 s

T_Wb = 1,402 s

T_Wk = 1,468 s

Dla krążka:

I_0kr = 0,003802912 kgm²

Dla koła zębatego:

I_0z = 0,005328038 kgm²

5. Analiza błędów

Błędu bezwzględne pomiaru ciężaru P, pomiaru długości L oraz pomiarów czasów T_Wb, T_Wk, T_W ustalam następująco:

P = 0,1N

L = 0,001 m

T_Wb = 0,01s

T_Wk 0,01 s

T_W = 0,01 s

dla krążka:

błąd bezwzględny

I_0kr = 0,001233415 kgm²

błąd względny

dla koła zębatego:

błąd bezwzględny:

I_0kr = 0,001704335 kgm²

błąd względny:

Moment bezwładności wyznaczony analitycznie:

Analitycznie wyznaczam moment bezwładności dla krążka z otworem o średnicy r = 0,0075 m, średnicy zewnętrznej R = 0,048 m i masie m = 2,205 kg

6. Wnioski:

Wpływ na błędy pomiarowe miały przede wszystkim:

• Niedokładność studentów

• Niedokładność przyrządów pomiarowych

• Zła technika pomiaru

Przy wyznaczaniu momentu bezwładności bryły wielkością obarczoną błędem pomiaru był okres ruchu wahadłowego bryły (dlatego mierzony był czas większej liczby okresów T i do obliczeń przyjęta była wartość średnia). Mieliśmy podane wartości masy oraz dokładnie zmierzoną odległość środka masy od osi zawieszenia, dlatego te wielkości wpływają w małym stopniu na błąd pomiaru.

Masowe momentu bezwładności dla krążka wyznaczone :

1.doświadczalnie metodą ruchu obrotowego:

I₀ = 0,0010163727610,0000523443844 Ns²m

2. doświadczalnie metodą wahadła fizycznego:

I_0kr = 0,003802912 kgm² ± 0,001233415 kgm²

3.analitycznie

I₀ = 0,002602175

Wszystkie z otrzymanych wyników obarczone są pewnym błędem - nawet w metodzie analitycznej błędy mogły wystąpić np. przy pomiarze średnicy czy wyznaczaniu masy krążka. Z otrzymanych wyników można wywnioskować, że metoda ruchu obrotowego jest najmniej dokładna, dlatego, że występowało tarcie między elementami współpracującymi oraz z zastosowania nici, która była rozciągliwa i ważka (czynniki te nie były uwzględniane podczas obliczeń).

6

---