Momenty bezwładności figur płaskich - definicje i wzory

Dana jest figura płaska o polu A oraz prostokątny układ współrzędnych Oxy.

Momentem bezwładności figury względem osi x jest

dA

y

I

A

x

∫

=

2

.

Momentem bezwładności figury względem osi y jest

dA

x

I

A

y

∫

=

2

.

Momentem dewiacyjnym figury względem prostokątnego układu osi x i y jest

∫

=

A

xy

xydA

I

.

Z definicji momentów bezwładności wynika, że mogą być one tylko dodatnie.

Natomiast moment dewiacyjny może być dodatni, ujemny lub równy zero.

W przypadku równoległego przesunięcia osi układu korzystamy z twierdzenia

Steinera, wyrażonego poniższymi wzorami:

y

y

x

x

O

A

dA

a

b

x

c

y

c

y

x

A

C(b, a)

O

2

a

A

I

I

c

x

x

⋅

+

=

2

b

A

I

I

c

y

y

⋅

+

=

b

a

A

I

I

c

c

y

x

xy

⋅

⋅

+

=

gdzie osie

x

c

i

y

c

są osiami centralnymi, natomiast

b i a są współrzędnymi punktu C w

układzie

Oxy. Z rysunku wynika, że są to odległości między osiami.

Osiowe momenty bezwładności oraz dewiacyjny moment figury względem osi

centralnych można wyznaczyć korzystając z przekształconych wzorów Steinera:

2

a

A

I

I

x

x

c

⋅

−

=

2

b

A

I

I

y

y

c

⋅

−

=

b

a

A

I

I

xy

y

x

c

c

⋅

⋅

−

=

.

Przyjmijmy

prostokątny układ współrzędnych

Oξη obrócony o kąt φ względem układu

Oxy. Współrzędne dowolnego punktu figury płaskiej spełniają zależności:

ξ = x cos φ + y sin φ

η = y cos φ − x sin φ.

ξ

x

O

y

η

φ

A

φ

y

η

ξ

x

Wykorzystując te zależności wyznaczamy momenty bezwładności i moment
dewiacyjny w obróconym układzie

Oξη:

ϕ

ϕ

−

ϕ

+

ϕ

=

=

∫

cos

sin

I

sin

I

cos

I

dA

η

I

xy

y

x

A

ξ

2

2

2

2

ϕ

ϕ

+

ϕ

+

ϕ

=

=

∫

cos

sin

I

sin

I

cos

I

dA

ξ

I

xy

x

y

A

η

2

2

2

2

(

)

(

)

ϕ

−

ϕ

+

ϕ

ϕ

−

=

=

∫

2

2

sin

cos

I

cos

sin

I

I

ξηdA

I

xy

y

x

A

ξη

lub

(

) (

)

ϕ

−

ϕ

−

+

+

=

2

2

2

2

sin

I

cos

I

I

I

I

I

xy

y

x

y

x

ξ

(

) (

)

ϕ

+

ϕ

−

−

+

=

2

2

2

2

sin

I

cos

I

I

I

I

I

xy

y

x

y

x

η

(

)

ϕ

+

ϕ

−

=

2

2

2

cos

I

sin

I

I

I

xy

y

x

ξη

.

Osie układu prostokątnego, w którym moment dewiacyjny

I

ξη

= 0 nazywamy

głównymi osiami bezwładności. Kąt φ

o

między osiami prostokątnego układu

Oxy i układu

głównych osi bezwładności spełnia równanie:

y

x

xy

I

I

I

tg

−

−

=

ϕ

2

2

o

Momenty bezwładności względem głównych osi bezwładności osiągają wartości

ekstremalne:

2

2

1

2

2

xy

y

x

y

x

max

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

2

2

2

2

2

xy

y

x

y

x

min

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

.

Z powyższych wzorów wynika, że

2

1

I

I

I

I

I

I

η

ξ

y

x

+

=

+

=

+

Główna oś bezwładności, względem której moment bezwładności ma wartość

tworzy z osią x kąt

, natomiast główna oś bezwładności, względem której

max

I

I

=

1

1

ϕ

2

moment bezwładności ma wartość

min

I

I

=

2

tworzy z osią x kąt

2

ϕ

. Kierunki główne

minimalnego i maksymalnego momentów bezwładności wyznaczamy następująco:

1. I

x

> I

y

to

, natomiast

o

1

ϕ

=

ϕ

2

o

2

π

+

ϕ

=

ϕ

2. I

x

< I

y

to

2

o

1

π

+

ϕ

=

ϕ

, natomiast

o

2

ϕ

=

ϕ

3. I

x

= I

y

, I

xy

> 0 to

4

1

π

−

=

ϕ

, natomiast

4

2

π

=

ϕ

4. I

x

= I

y

, I

xy

< 0 to

4

1

π

=

ϕ

, natomiast

4

2

π

−

=

ϕ

.

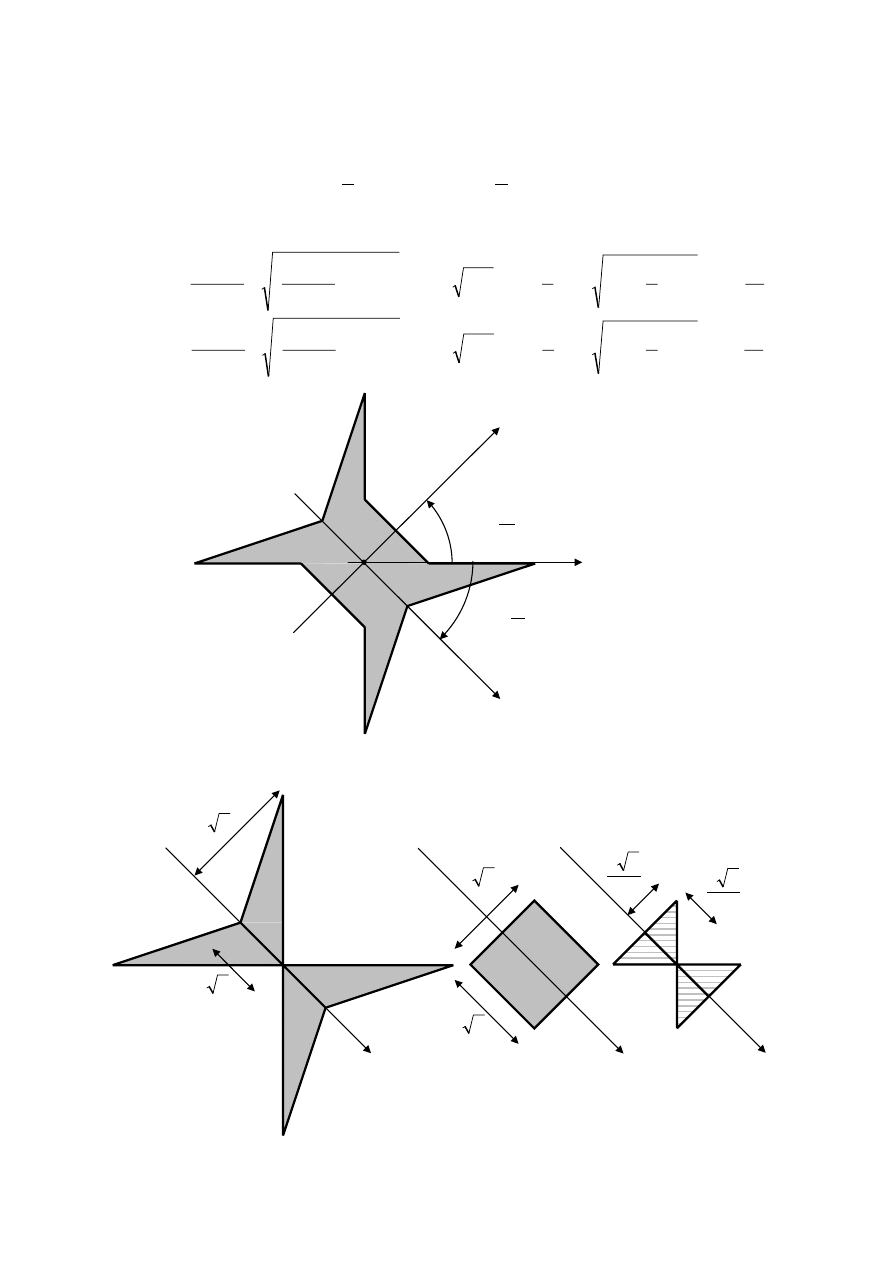
Znak dodatni bądź ujemny kąta φ ilustruje poniższy rysunek.

y

y

x

O

φ > 0

O

φ < 0

x

O głównych centralnych osiach bezwładności mówimy wówczas, gdy układ osi

głównych ma początek w środku ciężkości rozpatrywanej figury płaskiej. Momenty
bezwładności względem tych osi nazywamy głównymi centralnymi momentami
bezwładności.

Jeżeli jedna z osi układu współrzędnych jest osią symetrii figury płaskiej, to moment

dewiacyjny figury w takim układzie współrzędnych jest równy zero.

W przypadku wyznaczania momentów bezwładności i momentu dewiacyjnego figury

złożonej będziemy stosować metodę superpozycji, traktując rozpatrywaną figurę jako sumę
figur elementarnych, takich jak np. prostokąt, trójkąt i fragment koła. Korzystać będziemy z
wartości momentów bezwładności i momentu dewiacyjnego dla wymienionych figur.
1. Prostokąt

y

O

b

y

c

C

2

b

2

h

h

y

b

dA

=dxdy

y

O

x

dx

dy

h

x

c

x

x

3

0 0

2

2

3

1

bh

dxdy

y

dA

y

I

b h

A

x

∫∫

∫

=

=

=

3

3

0 0

2

2

3

1

hb

dxdy

x

dA

x

I

b h

A

y

=

=

=

∫∫

∫

2

2

0 0

4

1

h

b

xydxdy

xydA

I

b h

A

xy

∫∫

∫

=

=

=

3

2

3

2

12

1

2

3

1

2

bh

h

bh

bh

h

A

I

I

x

x

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

3

2

3

2

12

1

2

3

1

2

hb

b

bh

hb

b

A

I

I

y

y

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

0

2

2

4

1

2

2

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

h

b

bh

h

b

h

b

A

I

I

xy

y

x

c

c

2. Trójkąt

b

y

O

C

y

c

3

h

3

b

h

b

dA=dxdy

y

x

O

x

dx

y

dy

y=−

h

x

b

h

+

⋅

h

x

c

x

3

0

0

2

2

12

1

bh

dx

dy

y

dA

y

I

b

b

x

1

h

A

x

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

3

0

0

2

2

12

1

hb

dx

dy

x

dA

x

I

b

b

x

1

h

A

y

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

2

2

0

0

24

1

b

h

dx

dy

xy

dA

xy

I

b

b

x

1

h

A

xy

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

3

2

3

2

36

1

3

2

1

12

1

3

bh

h

bh

bh

h

A

I

I

x

x

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

3

2

3

2

36

1

3

2

1

12

1

3

hb

b

bh

hb

b

A

I

I

y

y

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

2

2

2

2

72

1

3

3

2

1

24

1

3

3

h

b

h

b

bh

h

b

h

b

A

I

I

xy

y

x

c

c

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

4

3. Ćwiartka koła

y

O

C

y

c

r

π

r

3

4

π

r

3

4

r

dA=ρdφdρ

x

O

ρ

y=ρsinφ

x=ρcosφ

dρ

φ

dφ

y

x

c

x

4

0 0

2

2

2

16

1

r

d

d

sin

dA

y

I

2 r

A

x

π

=

ρ

ϕ

ϕρ

ρ

=

=

∫∫

∫

π

4

0 0

2

2

2

16

1

os

r

d

d

c

dA

x

I

2 r

A

y

π

=

ρ

ϕ

ϕρ

ρ

=

=

∫∫

∫

π

4

0 0

2

8

1

os

r

d

d

c

sin

dA

xy

I

2 r

A

xy

∫∫

∫

π

=

ρ

ϕ

ϕρ

ϕ

ρ

=

=

4

2

2

4

2

05488

0

3

4

4

1

16

1

3

4

r

.

r

r

r

r

A

I

I

x

x

c

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

4

2

2

4

2

05488

0

3

4

4

1

16

1

3

4

r

.

r

r

r

r

A

I

I

y

y

c

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

4

2

2

4

2

01647

0

3

4

4

1

8

1

3

4

r

.

r

r

r

r

A

I

I

xy

y

x

c

c

−

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

4. Półkole

O

C

r

r

π

r

3

4

y

c

=y

x

c

x

4

4

8

1

16

1

2

πr

πr

I

I

y

x

=

⋅

⋅

=

=

5

4

2

2

4

10976

0

3

4

4

1

16

1

2

r

.

r

r

r

I

c

x

≅

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

⋅

=

0

=

=

xy

y

x

I

I

c

c

5. Kwadrat

y

c

C

y

c

C

a

x

c

x

c

a

4

12

1

a

I

I

c

c

y

x

=

=

0

=

c

c

y

x

I

W przypadku kwadratu momenty bezwładności i moment dewiacyjny w dowolnym

układzie osi centralnych przyjmują podane powyżej wartości.

Przykład I

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższego trójkąta

równoramiennego w układzie Oxy.

C

x

y

y

c

x

c

C

O

O

C

1

C

2

y

c

a

a

a

x

y

O

a

x~

c

3

−

=

a

y~

c

2

=

C

a

3a

y

x

c

x

6

Wprowadzamy

układ osi centralnych dla trójkąta. Oś x

c

jest osią symetrii figury.

Następnie dzielimy trójkąt równoramienny na dwa trójkąty prostokątne.

Moment bezwładności trójkąta równoramiennego względem osi x

c

jest sumą

momentów bezwładności względem tej osi dwu jednakowych trójkątów prostokątnych,
stykających się podstawą z osią x

c

.

4

3

2

1

3

12

1

2

a

a

a

I

c

x

=

⋅

⋅

⋅

=

Moment bezwładności trójkąta równoramiennego względem osi y

c

jest sumą

momentów bezwładności względem tej osi dwu jednakowych trójkątów prostokątnych. Na
osi y

c

leżą środki ciężkości obu trójkątów, a więc

( )

4

3

2

3

3

36

1

2

a

a

a

I

c

y

⋅

=

⋅

⋅

=

Moment dewiacyjny trójkąta równoramiennego względem układu osi x

c

y

c

jest równy

zero, gdyż oś x

c

jest osią symetrii rozpatrywanej figury.

0

=

c

c

y

x

I

Aby wyznaczyć momenty bezwładności i moment dewiacyjny dla trójkąta

równoramiennego w układzie Oxy należy skorzystać z twierdzenia Steinera. Pole powierzchni
trójkąta wynosi

2

3

2

3

2

1

a

a

a

A

=

⋅

⋅

=

.

( )

4

2

2

4

2

5

12

2

3

2

1

a

.

a

a

a

y~

A

I

I

c

x

x

=

⋅

+

=

⋅

+

=

(

)

4

2

2

4

2

5

28

3

3

2

3

a

.

a

a

a

x~

A

I

I

c

y

y

c

=

−

⋅

+

=

⋅

+

=

(

)

4

2

18

2

3

3

0

a

a

a

a

y~

x~

A

I

I

c

c

y

x

xy

c

c

−

=

⋅

−

⋅

+

=

⋅

⋅

+

=

Przykład II

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższego trójkąta w

układzie współrzędnych Oxy.

c

y

A

B

3a

6a

8a

5a

2a

3a

C

D

a

3

10

4a

x

6a

2a

6a

3a

O

y

x

8a

5a

6a

2a

4a

2a

y

O

Rozpatrywaną figurę otrzymamy odejmując figurę II od figury I.

7

4a

O

2a

2a

6a

8a

C

1

x

y

1

c

y

1

c

x

figura I

4a

6a

a

3

10

2a

5a

3a

3a

y

2a

6a x

2

c

y

2

c

x

figura II

4a

C

2

a

3

10

O

2

I

12

6

4

2

1

a

a

a

A

=

⋅

⋅

=

,

a

x~

c

3

10

1

=

,

a

y~

c

4

1

=

,

2

II

6

3

4

2

1

a

a

a

A

=

⋅

⋅

=

,

a

x~

c

3

10

2

=

,

a

y~

c

3

2

=

.

2

2

2

II

I

6

6

12

a

a

a

A

A

A

=

−

=

−

=

Moment bezwładności względem osi x wyznaczymy jako różnicę momentu

bezwładności względem osi x figury I i figury II.

(

)

( )

( )

( )

( )

4

2

2

2

2

2

3

2

2

II

II

2

1

I

I

II

I

159

3

6

3

4

36

1

4

12

6

4

36

1

2

1

a

a

a

a

a

a

a

a

a

y~

A

I

y~

A

I

I

I

I

c

x

c

x

x

x

x

c

c

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

⋅

−

⋅

+

⋅

⋅

=

=

⋅

+

−

⋅

+

=

−

=

W przypadku wyznaczania momentu bezwładności względem osi y nie musimy

dzielić figury. Bok BD trójkąta jest równoległy do osi y i do osi

. Moment bezwładności

względem osi

obliczymy korzystając ze wzoru

c

y

c

y

( )

4

3

3

3

16

4

3

36

1

36

1

a

a

a

h

b

I

c

y

=

⋅

⋅

=

⋅

⋅

=

Moment bezwładności względem osi y wyznaczymy z wykorzystaniem wzoru Steinera

4

2

2

4

2

a

72

3

10

6

3

16

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

=

⋅

+

=

a

a

a

x~

A

I

I

c

y

y

c

W celu obliczenia momentu dewiacyjnego traktujemy rozpatrywany trójkąt jako

różnicę figury I i figury II.

(

)

( ) ( )

( ) ( )

4

2

2

2

2

2

2

2

2

II

II

1

1

I

II

I

94

3

3

10

6

3

4

72

1

4

3

10

12

6

4

72

1

2

1

1

a

a

a

a

a

a

a

a

a

a

a

y~

x~

A

I

y~

x~

A

I

I

I

I

c

c

y

x

c

c

y

x

xy

xy

xy

c2

c

c

c

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

−

−

⋅

⋅

+

⋅

⋅

−

=

=

⋅

⋅

+

−

⋅

⋅

+

=

−

=

Przykład III

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższej figury w

układzie współrzędnych Oxy.

8

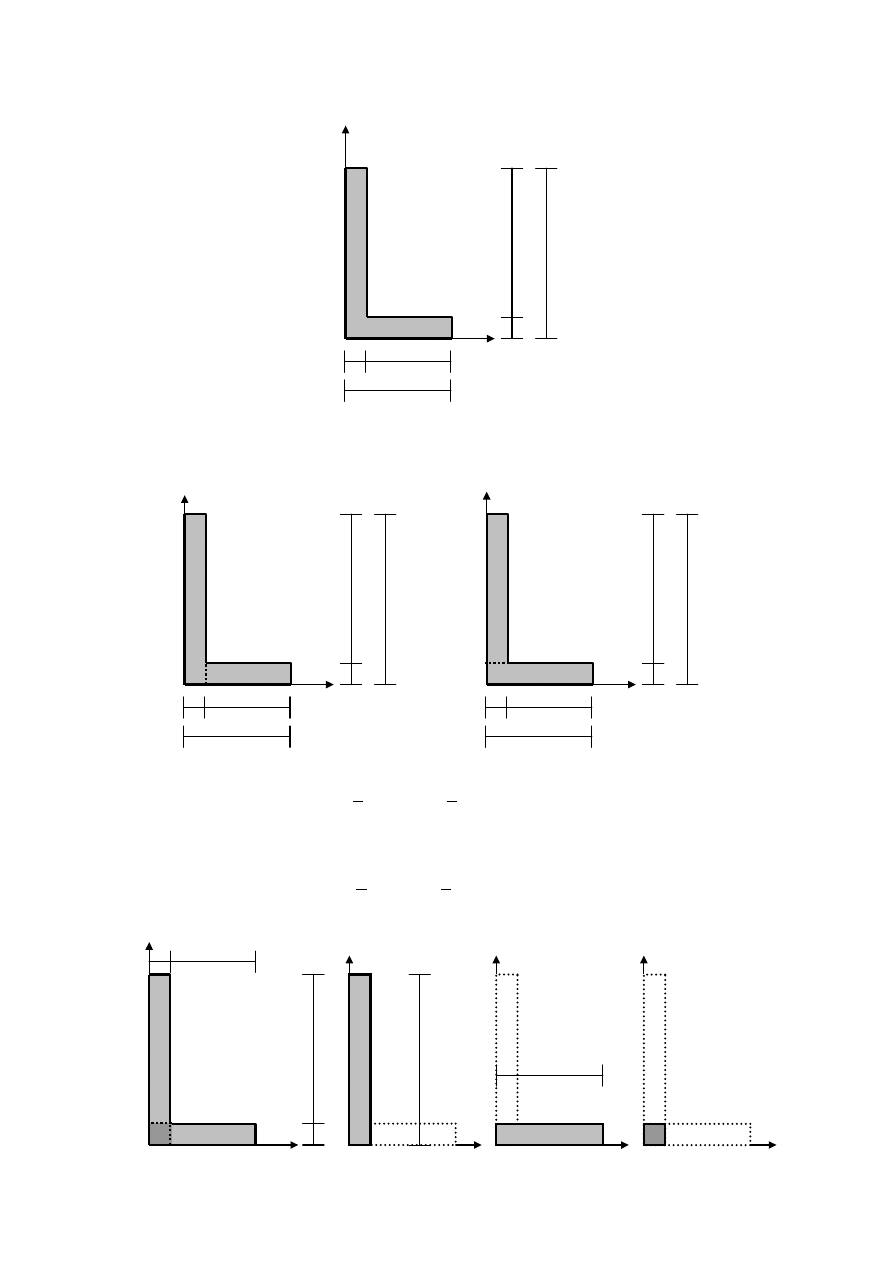
O

x

5a

a

4a

y

a

7a 8a

Przed wyznaczeniem momentu bezwładności rozpatrywanej figury względem osi x

dokonamy jej podziału na dwa prostokąty, tak żeby każdy prostokąt jednym bokiem stykał się
z osią x.

a

7a

4a

a

5a

8a

x

y

y

x

5a

a

4a

a

7a 8a

( )

4

3

3

172

4

3

1

8

3

1

a

a

a

a

a

I

x

=

⋅

⋅

+

⋅

⋅

=

W celu obliczenia momentu bezwładności figury względem osi y dokonamy jej

podziału na dwa prostokąty, z których każdy jednym bokiem styka się z osią y.

( )

4

3

3

44

5

3

1

7

3

1

a

a

a

a

a

I

y

=

⋅

⋅

+

⋅

⋅

=

Dla wyznaczenia momentu dewiacyjnego zastosujemy jeszcze inny podział.

a

7a

x

y

x

y

y

5a

4a

a

x

y

8a

x

9

Do obliczeń przyjmujemy figury składowe, zgodne z powyższym rysunkiem. Dwa

prostokąty o wymiarach 8a x a i a x 5a mają część wspólną w postaci kwadratu o boku a, dla
którego moment dewiacyjny będzie uwzględniony dwukrotnie. Należy więc w obliczeniach
moment dewiacyjny dla tego kwadratu, traktowanego jako trzecia figura, przyjąć ze znakiem
minus.

( )

( )

4

2

2

2

2

2

2

22

4

1

5

4

1

8

4

1

a

a

a

a

a

a

a

I

xy

=

⋅

⋅

−

⋅

⋅

+

⋅

⋅

=

.

10

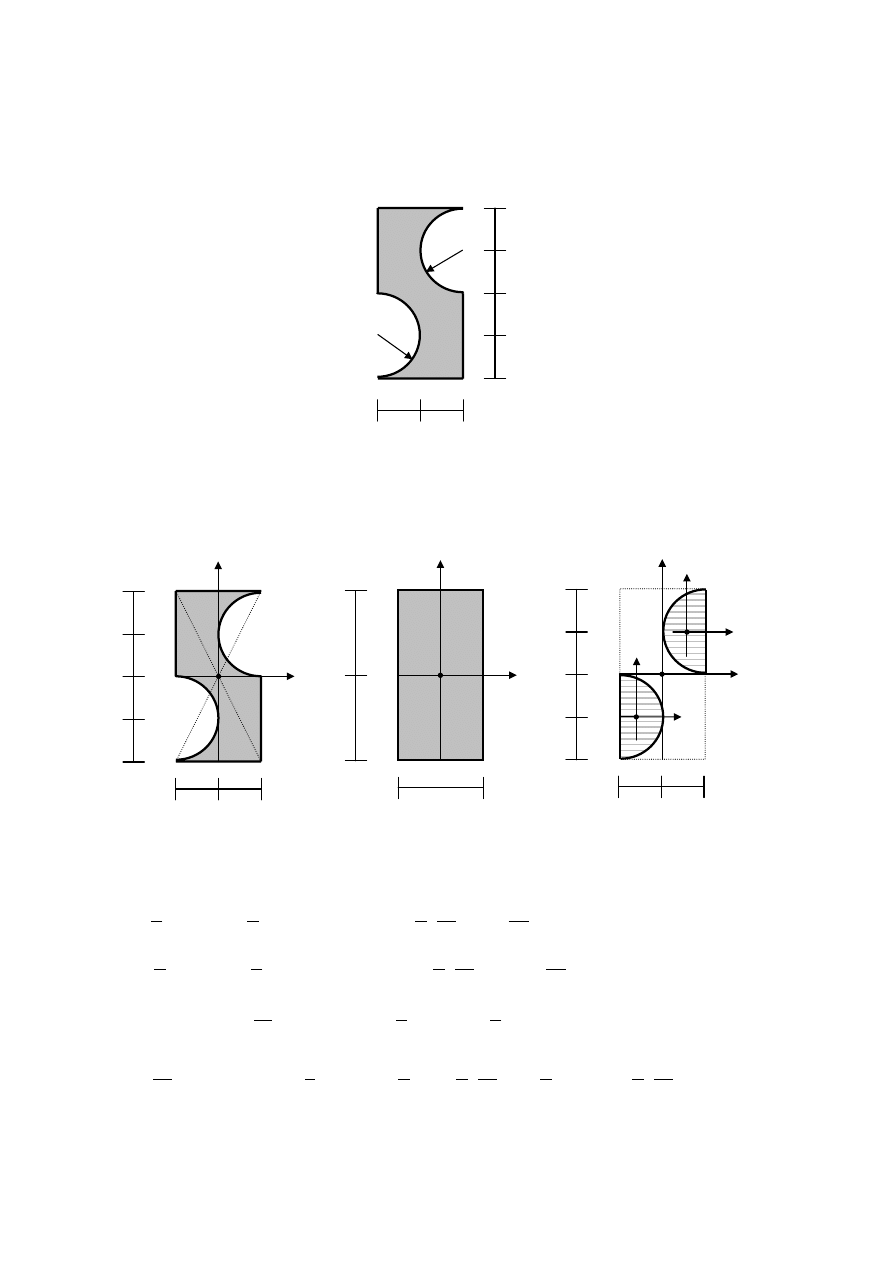
Przykład 2.1. Figura ze środkiem symetrii

Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury korzystając z metody analitycznej i graficznej (konstrukcja koła Mohra).

3r

3r

3r

3r

3r

3r

3r

3r

Rozpatrywana figura ma środek symetrii w punkcie przecięcia przekątnych prostokąta,

w który jest wpisana. Środek ciężkości figury leży w jej środku symetrii. Przez środek
symetrii prowadzimy osie centralne x i y . Następnie dzielimy figurę na prostokąt i dwa
półkola, które traktujemy jako pola ''ujemne''.

c

c

C

y

c

3r

3r

C

3

y

3

c

y

2

c

C

2

x

3

c

6r

C=C

1

y

c

3r

3r

C

y

c

3r

3r

3r

3r

6r

6r

3r

3r

3r

3r

x

2

c

x

c

x

c

x

c

W związku z tym, że własne osie centralne figury II i III (górnego i dolnego półkola)

nie pokrywają się z osiami centralnymi całej figury, będziemy korzystać z twierdzenia
Steinera. Wyznaczmy zatem pola powierzchni i współrzędne środków ciężkości dla tych figur
w układzie x y .

c

c

( )

2

2

II

2

9

3

2

1

πr

r

π

A

=

⋅

⋅

=

,

π

r

r

π

r

r

x~

c

4

3

3

3

4

3

2

−

=

⋅

−

=

,

r

y~

3

2

c

=

( )

2

2

III

2

9

3

2

1

πr

r

π

A

=

⋅

⋅

=

,

π

r

r

π

r

r

x~

c

4

3

3

3

4

3

3

+

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

−

=

,

r

y~

c

3

3

−

=

( )

( )

( )

4

2

2

4

3

91

545

3

2

9

3

8

1

2

12

6

12

1

r

.

r

πr

r

π

r

r

I

c

x

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

⋅

⋅

−

⋅

⋅

=

( )

( )

4

2

2

2

2

4

3

91

113

3

3

4

3

2

9

3

3

4

2

9

3

8

1

2

6

12

12

1

r

.

π

r

r

πr

π

r

πr

r

π

r

r

I

c

y

=

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

⋅

+

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛ ⋅

⋅

−

⋅

⋅

⋅

−

⋅

⋅

=

4

2

47

146

3

3

4

3

3

2

9

0

2

0

r

.

π

r

r

r

πr

I

c

c

y

x

−

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

⋅

⋅

+

⋅

−

=

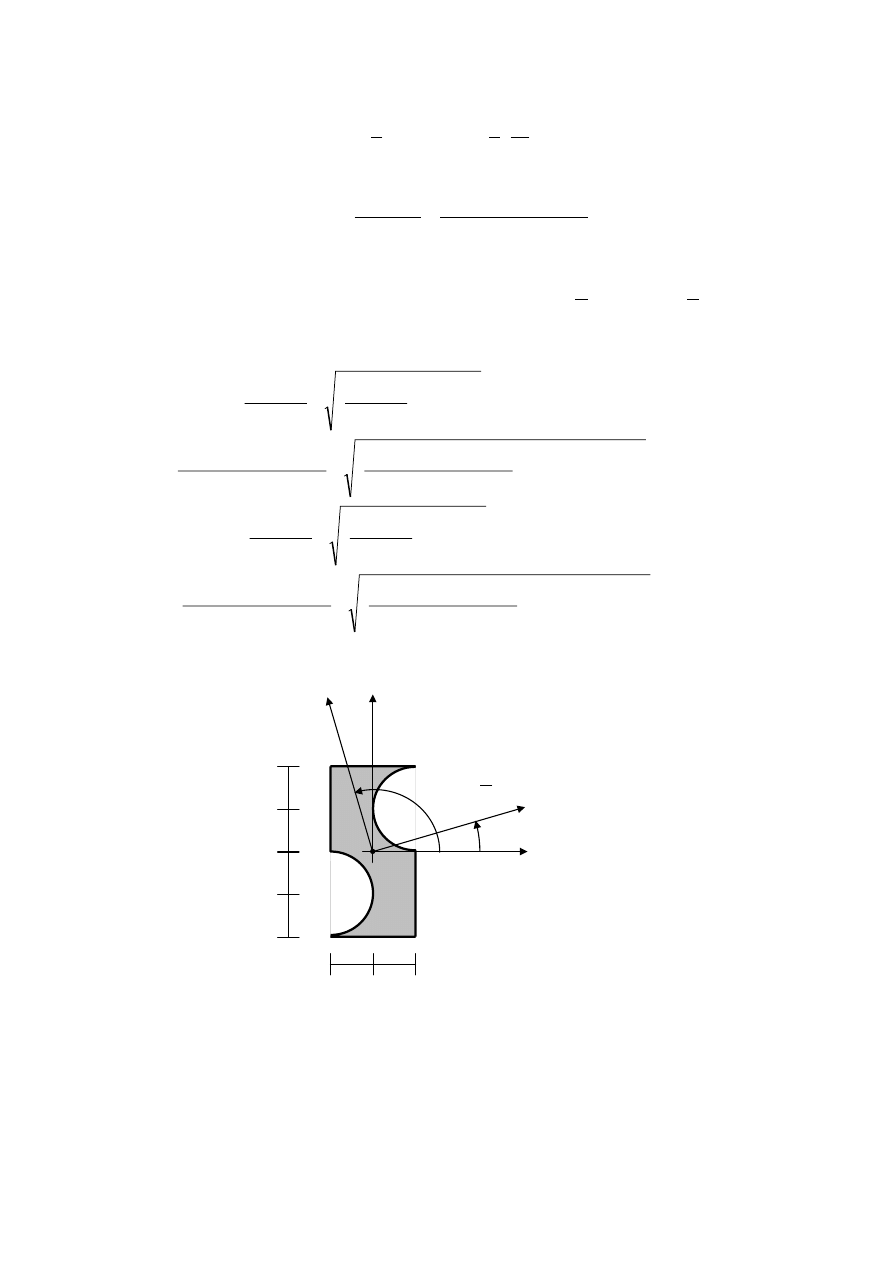
Wyznaczamy teraz kierunki główne.

(

)

6781

0

91

113

91

545

47

146

2

2

2

4

4

4

o

.

r

.

r

.

r

.

I

I

I

tg

C

C

C

C

y

x

y

x

=

−

−

⋅

−

=

−

−

=

ϕ

rad

5959

0

2

o

.

=

ϕ

,

rad

2979

0

o

.

=

ϕ

.

Ponieważ

>

to

c

x

I

c

y

I

o

1

ϕ

=

ϕ

=

0.2979 rad, natomiast

2

o

2

π

+

ϕ

=

ϕ

=

⎟

⎠

⎞

⎜

⎝

⎛

π

+

2

2979

0

.

rad =

=1.8687rad
Główne centralne momenty bezwładności przyjmują następujące wartości:

(

)

4

2

4

2

4

4

4

4

2

2

1

89

590

47

146

2

91

113

91

545

2

91

113

91

545

2

2

r

.

r

.

r

.

r

.

r

.

r

.

I

I

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

max

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

(

)

4

2

4

2

4

4

4

4

2

2

93

68

47

146

2

91

113

91

545

2

91

113

91

545

2

2

r

.

r

.

r

.

r

.

r

.

r

.

I

I

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

min

2

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

Na poniższym rysunku przedstawione są kierunki główne.

kierunek

I

max

kierunek

I

min

x

c

C

y

c

2

o

2

π

+

ϕ

=

ϕ

rad

2979

0

o

1

.

=

ϕ

=

ϕ

3

r

3r

3r

3r

3

r

3

r

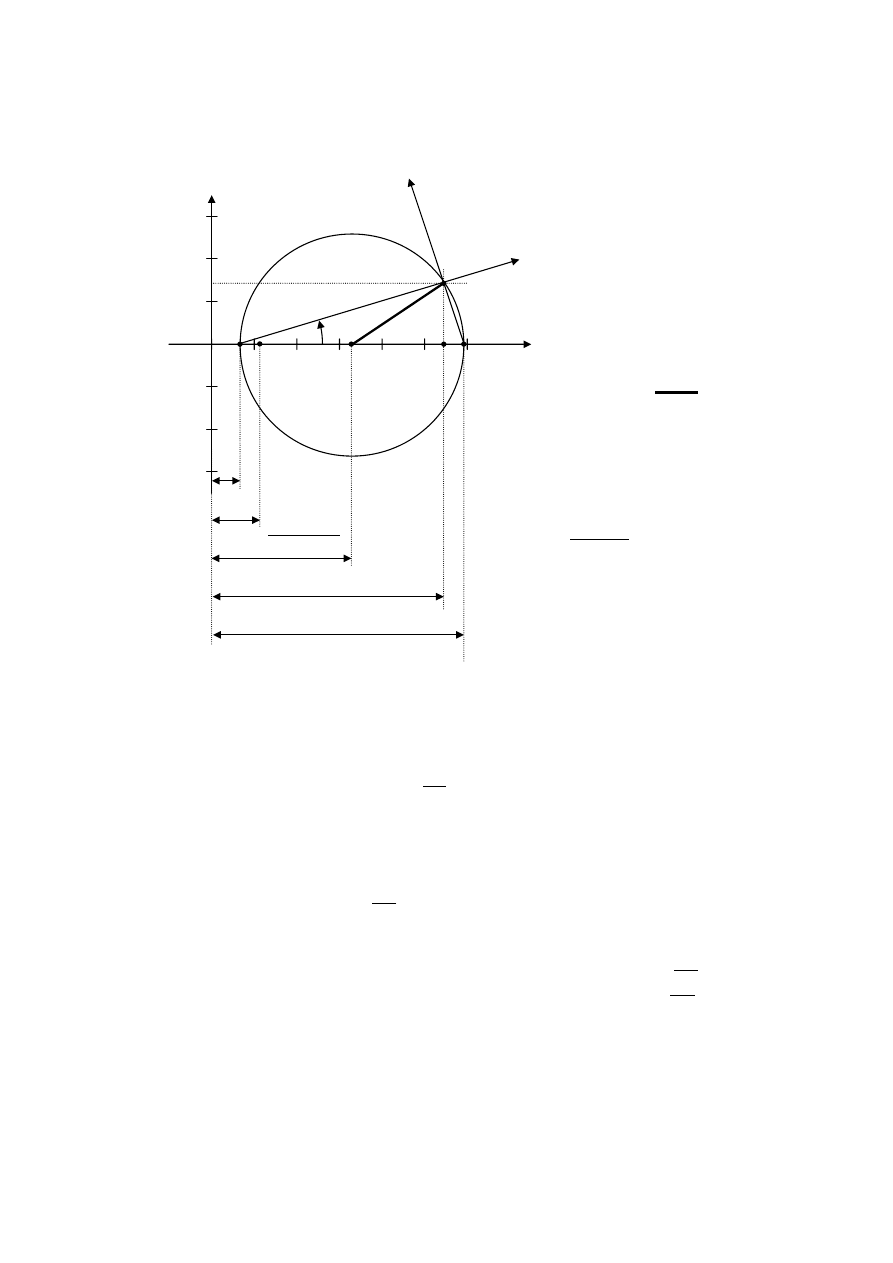
Główne centralne momenty bezwładności oraz kierunki główne można wyznaczyć

metodą graficzną, stosując konstrukcję koła Mohra. Korzystamy z wyznaczonych wartości
momentów bezwładności w układzie x y

c

c

4

91

545

r

.

I

c

x

=

,

,

4

91

113

r

.

I

c

y

=

oraz wartości momentu dewiacyjnego

2

4

47

146

r

.

I

c

c

y

x

−

=

.

Przyjęta skala: 100

r

4

Momenty dewiacyjne

Momenty bezwładności

O

o

ϕ

C

B

A

D

F

R

kierunek minimalnego
momentu bezwładności

kierunek maksymalnego
momentu bezwładności

E

c

y

I

(

)

2

+

c

c

y

x

I

I

1

I

2

I

c

x

I

( )

( )

(

)

(

)

( )

0

0

0

2

0

0

1

2

,

I

F

,

I

E

I

,

I

D

,

I

I

C

,

I

B

,

I

A

c

c

c

c

c

c

c

y

x

x

y

x

y

x

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

Kolejność postępowania przy rozwiązywaniu zadania metodą graficzną jest następująca:
1. Wyznaczenie położenia punktów

A i B

Wartości momentów bezwładności w układzie

x y

,

stanowią

odpowiednio współrzędne punktów

A(545.91r

c

c

4

91

545

r

.

I

c

x

=

4

91

113

r

.

I

c

y

=

4

,0) i

B(113. 91r

4

,0).

2. Wyznaczenie położenia punktu

C

Punkt

C(329.91r

4

,0) jest środkiem odcinka

AB i środkiem koła Mohra.

3. Wyznaczenie położenia punktu

D

Po uwzględnieniu wartości

oraz

otrzymamy współrzędne

4

91

545

r

.

I

c

x

=

4

47

146

r

.

I

c

c

y

x

−

=

punktu

D(545.91r

4

,−(−146.47

r

4

)), czyli

D(545.91r

4

,146.47

r

4

).

4. Wyznaczenie promienia koła Mohra
Łączymy punkty

C i D odcinkiem

CD

, który stanowi promień

R koła Mohra. Promieniem

tym zataczamy okrąg.
5. Wyznaczenie głównych momentów bezwładności
Koło Mohra przecina oś poziomą w dwu punktach:

E i F. Długość odcinka

OE

odpowiada

minimalnemu momentowi bezwładności

, natomiast długość odcinka

2

I

F

O

odpowiada

maksymalnemu momentowi bezwładności .

1

I

6. Wyznaczenie kierunków głównych
Oś przechodząca przez punkty

E i D jest osią maksymalnego momentu bezwładności, a oś

przechodząca przez punkty

F i D jest osią minimalnego momentu bezwładności.

3

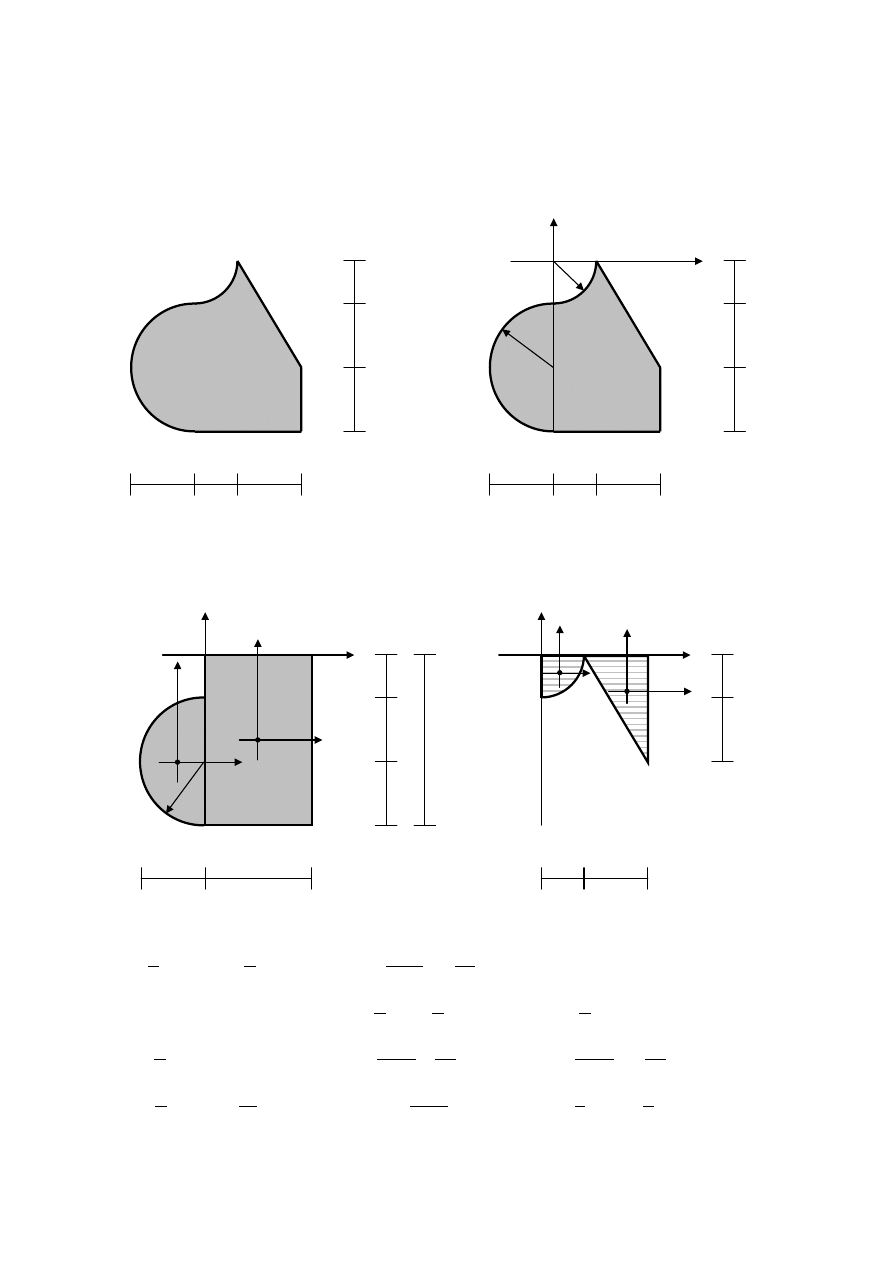
Przykład 2.2. Figura złożona

Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury.

2r

2r

3r

3r

3r

3r

3r

O

2r

y

x

2r

2r

3r

3r

3r

3r

W celu wyznaczenia środka ciężkości oraz obliczenia wartości momentów

bezwładności i momentu dewiacyjnego przyjmujemy układ współrzędnych Oxy oraz
dzielimy rozpatrywaną figurę na cztery figury podstawowe.

3r

5r

O

3r

3r

2r

3r

x

I II

1

C

C

1

c

x

1

c

y

2

c

x

2

c

y

2

III

2

r

2

r

3

r

3

r

O

x

y

IV

4

C

3

c

x

3

c

y

4

c

x

c

y

4

3

C

y

8r

Obliczamy pola figur składowych i określamy współrzędne ich środków ciężkości.

( )

2

2

I

2

9

3

2

1

πr

r

π

A

=

⋅

⋅

=

,

π

r

π

r

x~

c

4

3

3

4

1

−

=

⋅

⋅

−

=

,

r

y~

c

5

1

−

=

2

II

40

8

5

r

r

r

A

=

⋅

=

,

r

r

x~

c

2

5

5

2

1

2

=

⋅

=

,

r

r

y~

c

4

8

2

1

2

−

=

⋅

−

=

( )

2

2

III

2

4

1

πr

r

π

A

=

⋅

⋅

=

,

π

r

π

r

x~

c

3

8

3

2

4

3

=

⋅

⋅

=

,

π

r

π

r

y~

c

3

8

3

2

4

3

−

=

⋅

⋅

−

=

2

IV

2

15

5

3

2

1

r

r

r

A

=

⋅

⋅

=

,

r

r

r

x~

c

4

3

3

2

2

4

=

⋅

+

=

,

r

r

y~

c

3

5

5

3

1

4

−

=

⋅

−

=

Całkowite pole figury wynosi:

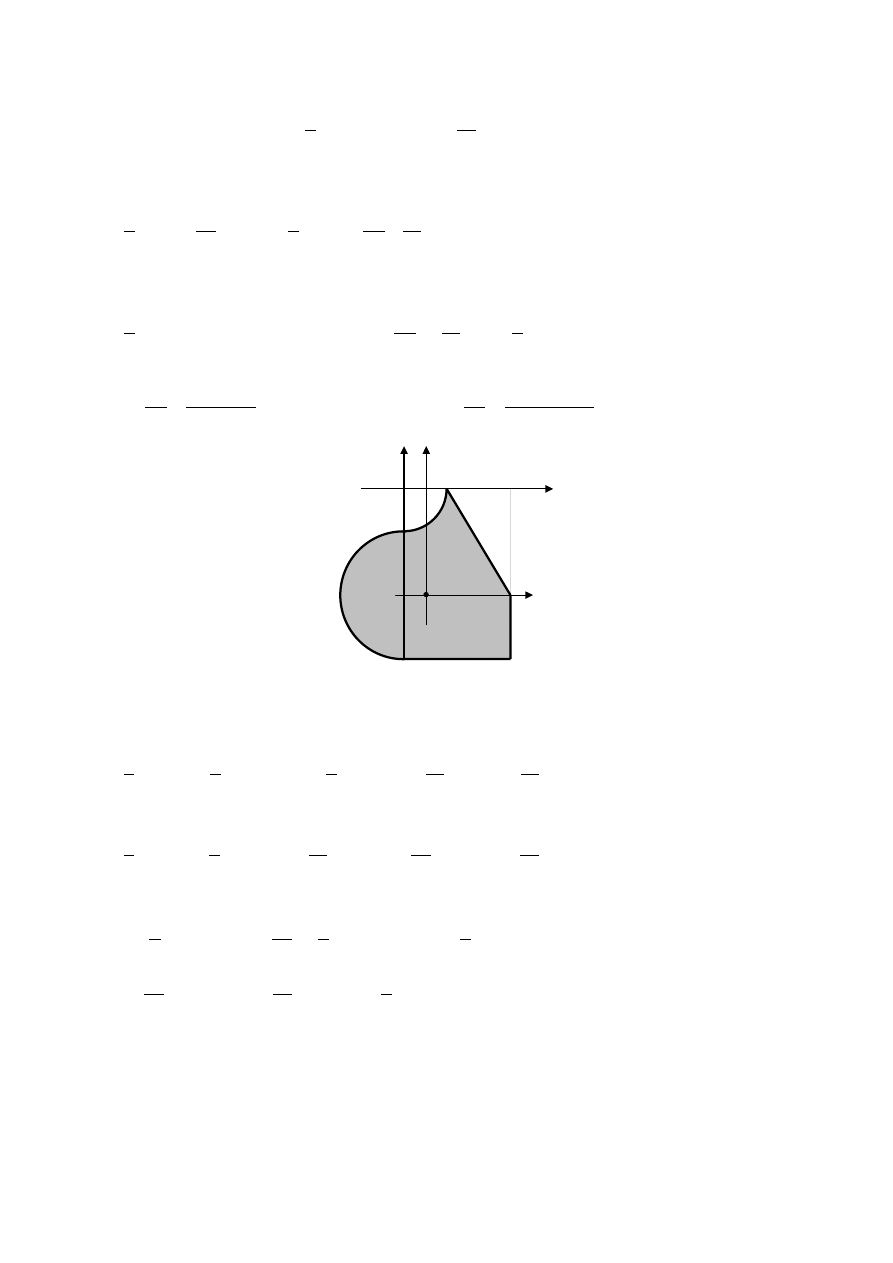
2

2

2

2

2

IV

III

II

I

496

43

2

15

40

2

9

r

.

r

πr

r

πr

A

A

A

A

A

=

−

−

+

=

−

−

+

=

Moment statyczny względem osi

y wynosi:

3

2

2

2

2

4

IV

3

III

2

II

1

I

333

.

49

4

2

15

3

8

2

5

40

4

2

9

r

r

r

π

r

πr

r

r

π

r

r

x~

A

x~

A

x~

A

x~

A

S

c

c

c

c

y

=

⋅

−

⋅

−

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

π

=

=

⋅

−

⋅

−

⋅

+

⋅

=

Moment statyczny względem osi

x wynosi:

(

)

(

)

3

2

2

2

2

4

IV

3

III

2

II

1

I

519

215

3

5

2

15

3

8

4

40

5

2

9

r

.

r

r

π

r

πr

r

r

r

r

y~

A

y~

A

y~

A

y~

A

S

c

c

c

c

x

−

=

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

−

−

⋅

+

−

⋅

π

=

=

⋅

−

⋅

−

⋅

+

⋅

=

Współrzędne środka ciężkości rozpatrywanej figury wynoszą odpowiednio:

r

.

r

.

r

.

A

S

x~

y

c

1342

1

496

43

333

49

2

3

=

=

=

oraz

r

.

r

.

r

A

S

~

x

c

9549

4

496

43

519

.

215

y

2

3

−

=

−

=

=

.

x

y

O

C

c

x

c

y

Wyznaczymy momenty bezwładności i moment dewiacyjny w układzie Oxy.

( )

(

)

( )

( )

( )

4

3

4

3

2

2

4

IV

III

II

I

18

1204

5

3

12

1

2

16

1

8

5

3

1

5

2

9

3

8

1

r

.

r

r

r

π

r

r

r

πr

r

π

I

I

I

I

I

x

x

x

x

x

=

⋅

⋅

−

⋅

−

⋅

⋅

+

−

⋅

+

⋅

=

=

−

−

+

=

( )

( )

( )

( )

( )

4

2

2

3

4

3

4

IV

III

II

I

25

238

4

2

15

3

5

36

1

2

16

1

5

8

3

1

3

8

1

r

.

r

r

r

r

r

π

r

r

r

π

I

I

I

I

I

y

y

y

y

y

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

⋅

−

⋅

−

⋅

⋅

+

⋅

=

=

−

−

+

=

(

)

( ) ( )

( )

( ) ( )

( )

4

2

2

2

4

2

2

2

IV

III

II

I

88

254

3

5

4

2

15

3

5

72

1

2

8

1

5

8

4

1

4

5

2

9

0

r

.

r

r

r

r

r

r

r

r

r

r

πr

I

I

I

I

I

xy

xy

xy

xy

xy

−

=

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

⋅

+

⋅

⋅

−

−

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

−

⋅

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛

π

−

⋅

−

⋅

+

=

=

−

−

+

=

Następnie wyznaczymy momenty bezwładności i moment dewiacyjny w układzie osi
centralnych x i y korzystając z przekształconych wzorów Steinera:

c

c

(

)

4

2

2

4

2

c

31

136

9549

4

496

43

18

1204

r

.

r

.

r

.

r

.

y~

A

I

I

x

x

c

=

−

⋅

−

=

⋅

−

=

(

)

4

2

2

4

2

c

30

182

1342

1

496

43

25

238

r

.

r

.

r

.

r

.

x~

A

I

I

y

y

c

=

⋅

−

=

⋅

−

=

2

(

)

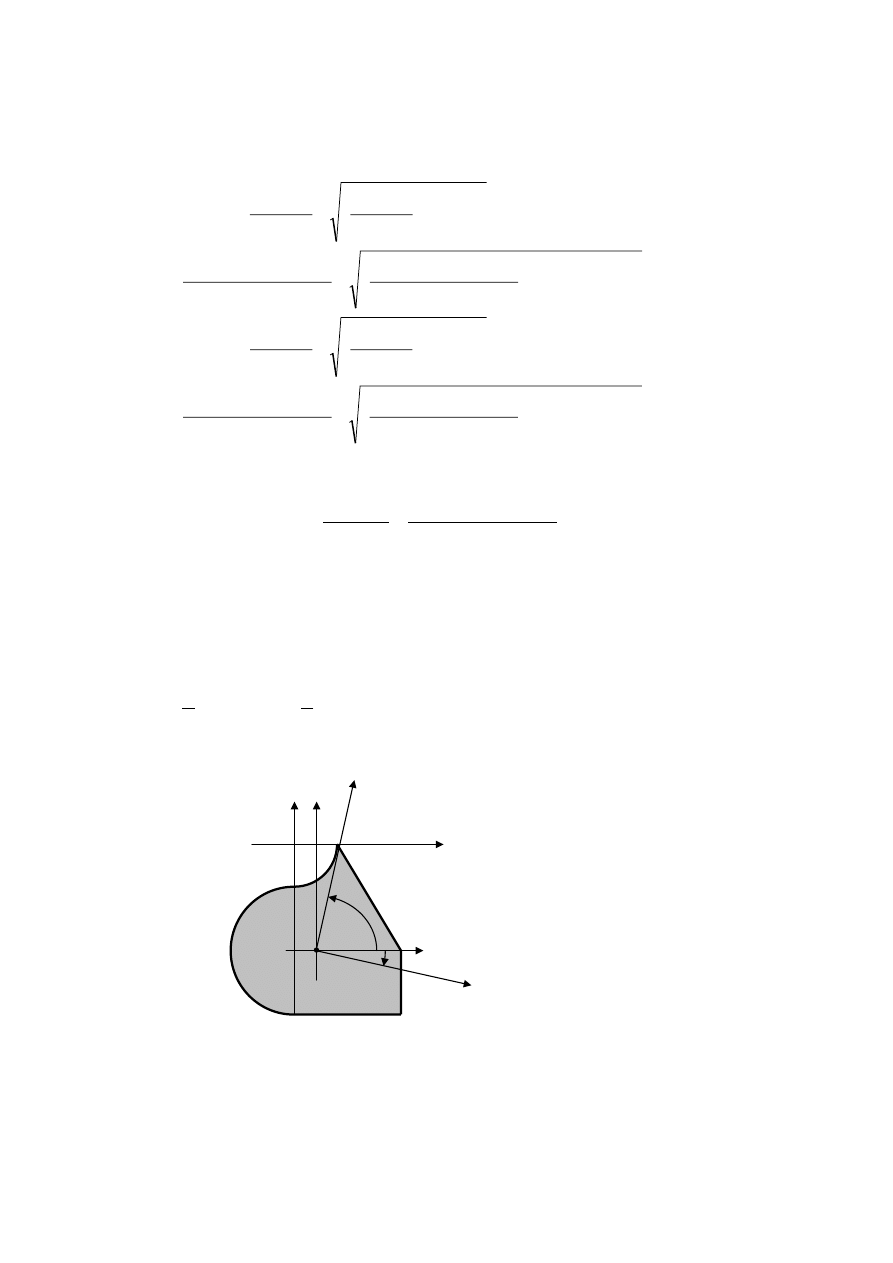
4

2

4

c

c

44

10

9549

4

1342

1

496

43

88

254

r

.

r

.

r

.

r

.

r

.

y~

x~

A

I

I

xy

y

x

c

c

−

=

−

⋅

⋅

−

−

=

⋅

⋅

−

=

.

Momenty bezwładności względem głównych centralnych osi bezwładności osiągają

wartości:

(

)

4

2

4

2

4

4

4

4

2

2

1

56

184

44

10

2

30

182

31

136

2

30

182

31

136

2

2

r

.

r

.

r

.

r

.

r

.

r

.

I

I

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

max

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

(

)

4

2

4

2

4

4

4

4

2

2

2

05

134

44

10

2

30

182

31

136

2

30

182

31

136

2

2

r

.

r

.

r

.

r

.

r

.

r

.

I

I

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

min

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

Kąt φ

o

między osiami centralnymi x y i głównymi centralnymi osiami bezwładności

spełnia równanie:

c

c

(

)

4540

0

30

182

31

136

44

10

2

2

2

4

4

4

o

.

r

.

r

.

r

.

I

I

I

tg

c

c

c

c

y

x

y

x

−

=

−

−

⋅

−

=

−

⋅

−

=

ϕ

stąd

,

.

rad

4262

0

2

o

.

−

=

ϕ

rad

2131

0

o

.

−

=

ϕ

Główna oś bezwładności, względem której moment bezwładności ma wartość

tworzy z osią

kąt

, natomiast główna oś bezwładności, względem której

moment bezwładności ma wartość

max

I

I

=

1

c

x

1

ϕ

min

I

I

=

2

tworzy z osią kąt

c

x

2

ϕ

.

W związku z tym, że

<

to:

c

x

I

c

y

I

rad

3577

1

rad

2

2131

0

2

o

1

.

π

.

=

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

π

+

ϕ

=

ϕ

, zaś rad

2131

0

o

2

.

−

=

ϕ

=

ϕ

.

x

y

O

C

c

x

c

y

1

ϕ

2

ϕ

Kierunek minimalnego
momentu bezwładności

Kierunek maksymalnego
momentu bezwładności

3

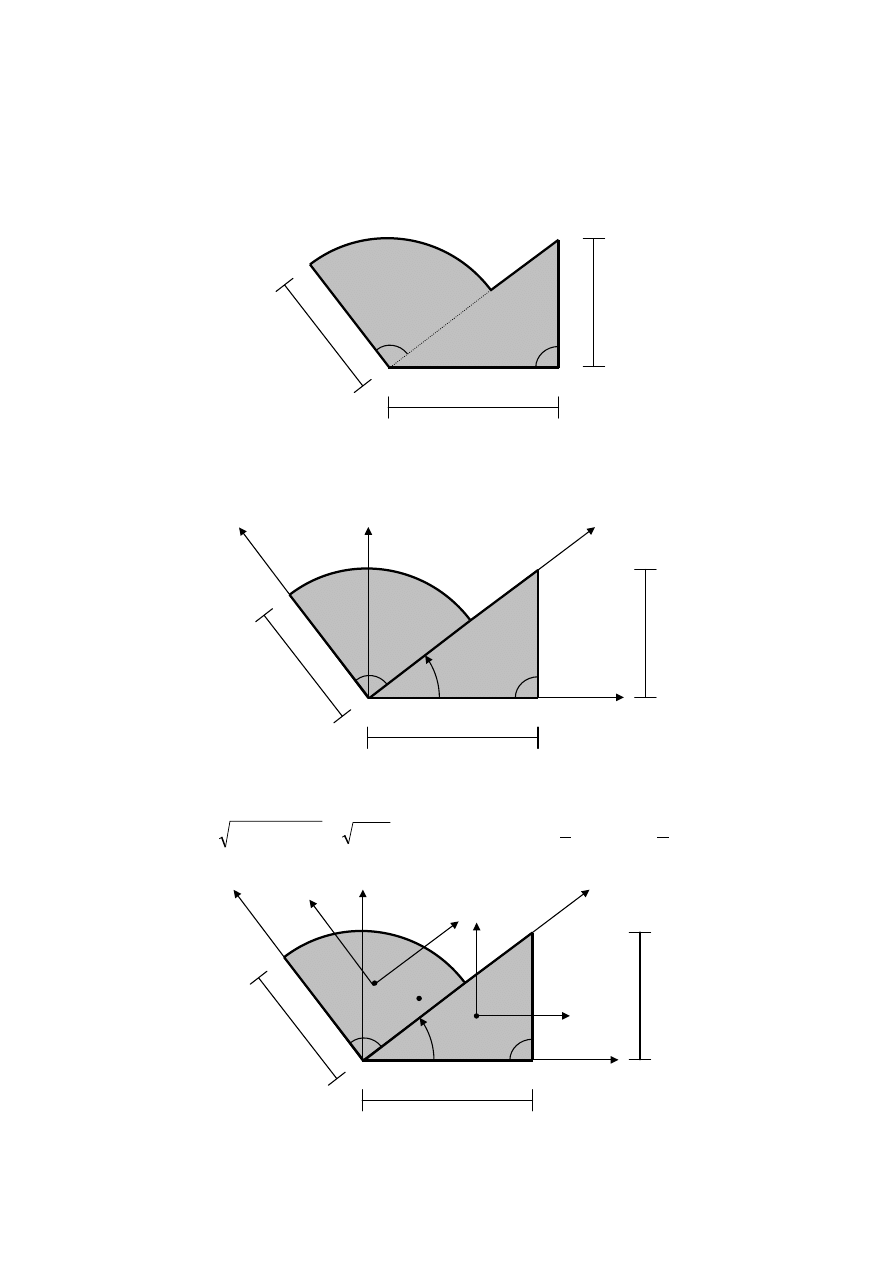
Przykład 2.3. Figura złożona

Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury.

·

4r

3r

·

3r

W celu wyznaczenia środka ciężkości oraz obliczenia wartości momentów

bezwładności i momentu dewiacyjnego przyjmujemy dwa współśrodkowe prostokątne układy
współrzędnych Oxy i Ouv oraz dzielimy rozpatrywaną figurę na dwie figury podstawowe.

v

I

II

3r

α

4r

·

·

x

O

3r

y

u

Z wymiarów zadania wynika, że przeciwprostokątna trójkąta (figura II) ma długość

równą :

( ) ( )

r

r

r

r

5

25

4

3

2

2

2

=

=

+

, a więc

5

3

=

α

sin

,

5

4

=

α

cos

.

3r

3r

4r

·

·

C

1

C

2

v

O

α

II

I

u

y

x

C

2

c

x

2

c

y

1

c

u

1

c

v

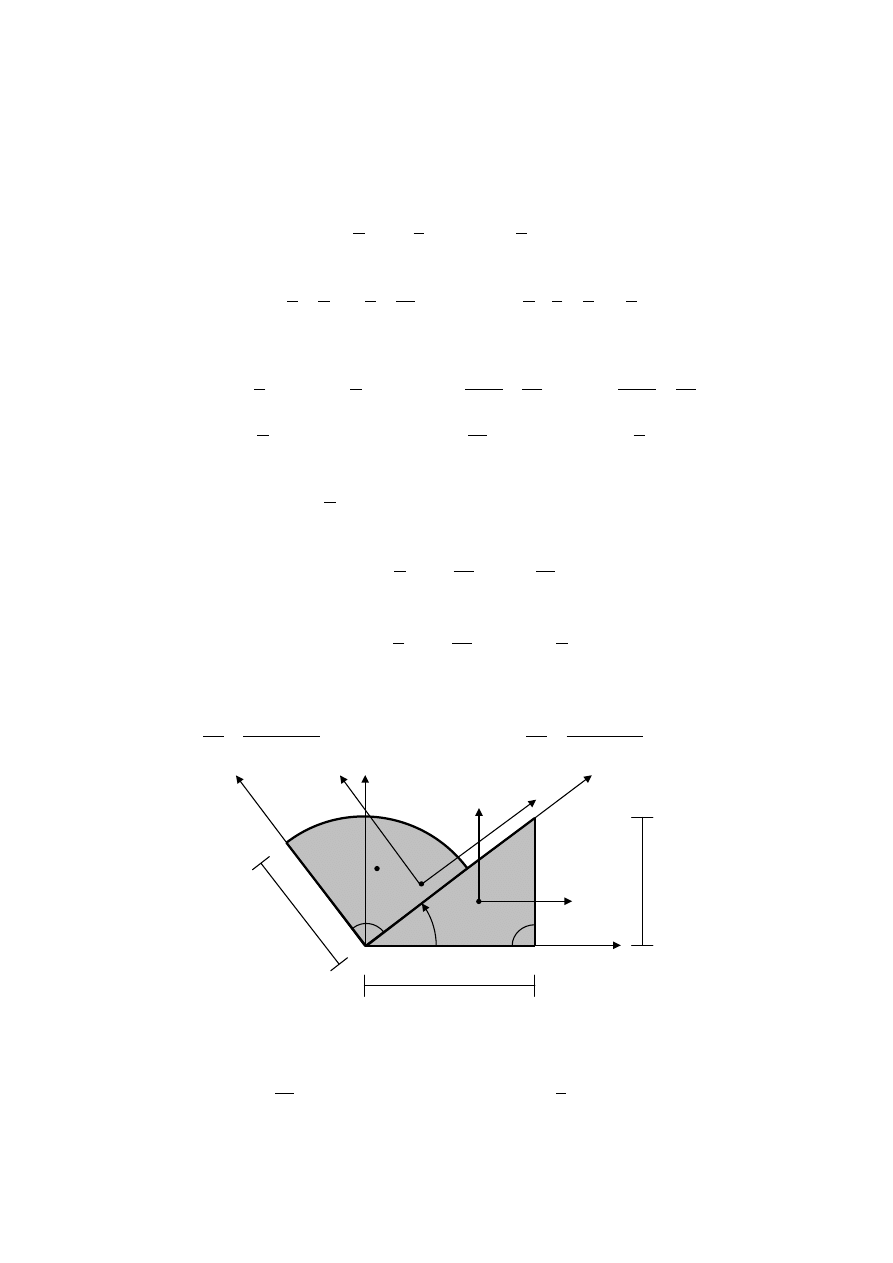
Układ współrzędnych Ouv obrócony jest o kąt α względem układu Oxy. Współrzędne

dowolnego punktu spełniają zależności:

u = x cos α + y sin α

v = y cos α − x sin α.

Współrzędne środka ciężkości trójkąta (II figury) w układzie Oxy są równe:

r

r

x~

c

3

8

4

3

2

2

=

⋅

=

,

r

r

y~

c

=

⋅

=

3

3

1

2

zaś w układzie Ouv przyjmują wartości:

r

r

r

u~

c

15

41

5

3

5

4

3

8

2

=

⋅

+

⋅

=

,

r

r

r

v~

c

5

4

5

3

3

8

5

4

2

−

=

⋅

−

⋅

=

Obliczamy pola figur składowych i określamy współrzędne ich środków ciężkości w

układzie Ouv.

( )

2

2

I

4

9

3

4

1

πr

r

π

A

=

⋅

⋅

=

,

π

r

π

r

u~

c

4

3

3

4

1

=

⋅

=

,

π

r

π

r

v~

c

4

3

3

4

1

=

⋅

=

,

2

II

6

3

4

2

1

r

r

r

A

=

⋅

⋅

=

,

r

u~

c

15

41

2

=

,

r

v~

c

5

4

2

−

=

.

Całkowite pole figury wynosi:

2

2

2

II

I

0686

13

6

4

9

r

.

r

πr

A

A

A

=

+

⋅

=

+

=

Moment statyczny względem osi v wynosi:

3

2

2

2

II

1

I

4

25

15

41

6

4

4

9

r

.

r

r

π

r

r

u~

A

u~

A

S

c

c

v

=

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

π

=

⋅

+

⋅

=

Moment statyczny względem osi u wynosi:

3

2

2

2

II

1

I

2

4

5

4

6

4

4

9

r

.

r

r

π

r

r

v~

A

v~

A

S

c

c

u

=

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

π

=

⋅

+

⋅

=

Współrzędne środka ciężkości rozpatrywanej figury w układzie Ouv wynoszą

odpowiednio:

r

.

r

.

r

.

A

S

u~

v

c

9436

1

0686

13

4

25

2

3

=

=

=

oraz

r

.

r

.

r

A

S

v~

u

c

3214

0

0686

13

2

.

4

2

3

=

=

=

.

3r

3r

4r

·

·

C

1

C

2

v

α

II

I

u

y

x

C

c

u

c

v

2

c

y

2

c

x

Wyznaczymy momenty bezwładności i moment dewiacyjny dla obu figur składowych

w układzie osi Ouv. Dla pierwszej figury (ćwiartka koła) mamy

( )

4

4

I

I

904

15

3

16

1

r

.

r

π

I

I

v

u

=

⋅

⋅

=

=

,

( )

4

4

I

125

10

3

8

1

r

.

r

I

uv

=

⋅

=

.

Dla drugiej figury (trójkąt) obliczenia przeprowadzimy w układzie osi Oxy.

2

( )

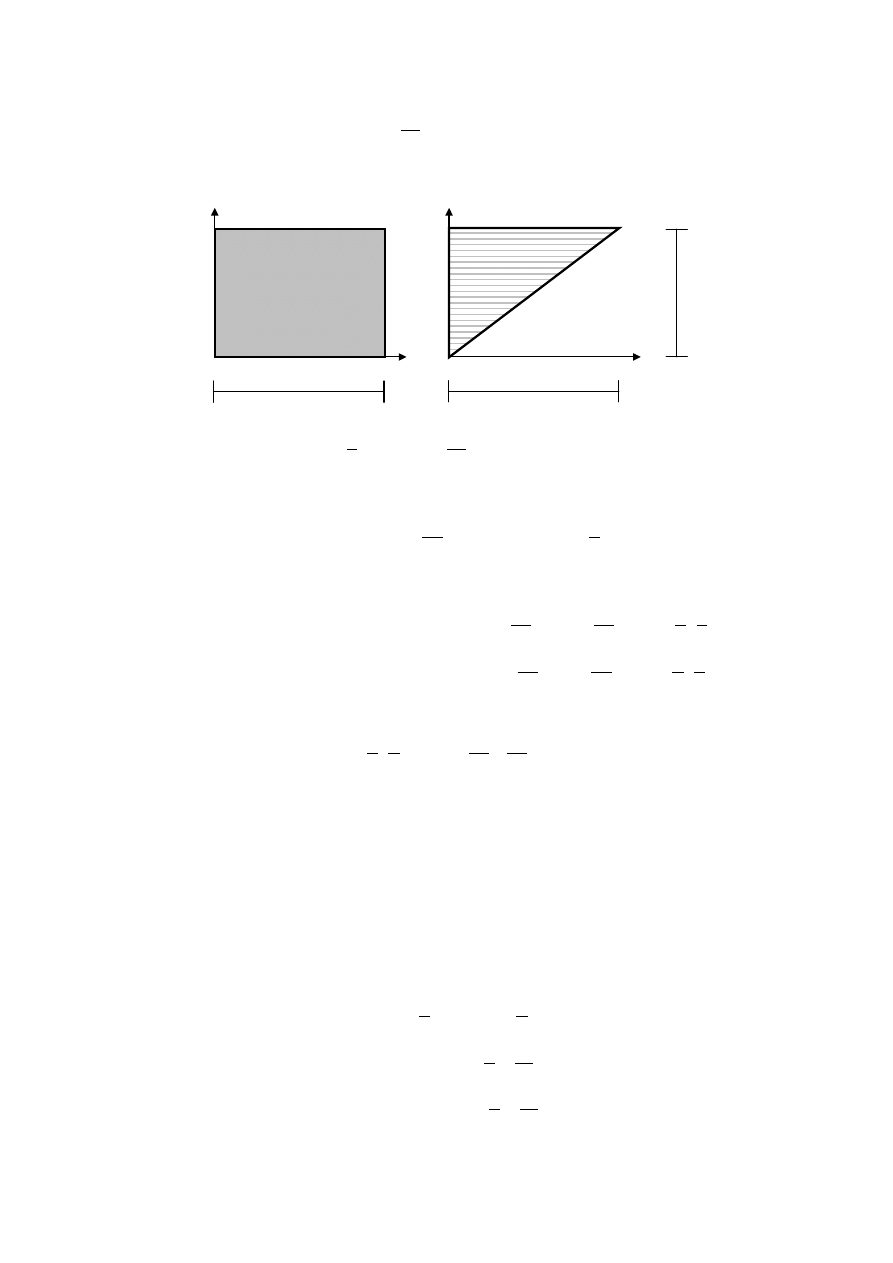
4

3

II

9

3

4

12

1

r

r

r

I

x

=

⋅

⋅

=

W celu wyznaczenia momentu bezwładności względem osi y figury II, przedstawimy

ją jako różnicę dwu figur, zgodnie z poniższym rysunkiem.

y

x

O

4r

O

4r

y

3r

x

( )

( )

4

3

3

II

48

4

3

12

1

4

3

3

1

r

r

r

r

r

I

y

=

⋅

⋅

−

⋅

⋅

=

Moment dewiacyjny figury II w układzie Oxy wyznaczymy korzystając z twierdzenia

Steinera

( ) ( )

4

2

2

2

II

II

18

3

8

6

3

4

72

1

2

2

r

r

r

r

r

r

y~

x~

A

I

I

c

c

II

y

x

xy

c

c

=

⋅

⋅

+

⋅

⋅

=

⋅

⋅

+

=

.

Momenty bezwładności i moment dewiacyjny figury II w obróconym układzie Ouv

wyznaczamy z zależności:

4

4

4

4

II

2

II

2

II

76

5

5

3

5

4

18

25

9

48

25

16

9

2

r

.

r

r

r

cos

sin

I

sin

I

cos

I

I

xy

y

II

x

u

=

⋅

⋅

−

⋅

+

⋅

=

α

α

−

α

+

α

=

4

4

4

4

II

2

II

2

II

II

24

51

5

3

5

4

18

25

9

9

25

16

48

2

r

.

r

r

r

cos

sin

I

sin

I

cos

I

I

xy

x

y

v

=

⋅

⋅

+

⋅

+

⋅

=

α

α

+

α

+

α

=

(

)

(

)

(

)

4

4

4

4

2

2

II

II

II

II

68

13

25

9

25

16

18

5

4

5

3

48

9

r

.

r

r

r

sin

cos

I

cos

sin

I

I

I

xy

y

x

uv

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

+

⋅

⋅

−

=

=

α

−

α

+

α

α

−

=

Momenty bezwładności i moment dewiacyjny rozważanej figury, będącej sumą figury

I i II, w obróconym układzie Ouv obliczymy jako sumy momentów dla figur składowych.

4

4

4

II

I

664

21

76

5

904

15

r

.

r

.

r

.

I

I

I

u

u

u

=

+

=

+

=

4

4

4

II

I

144

67

24

51

904

15

r

.

r

.

r

.

I

I

I

v

v

v

=

+

=

+

=

4

4

4

II

I

555

3

68

13

125

10

r

.

r

.

r

.

I

I

I

uv

uv

uv

−

=

−

=

+

=

.

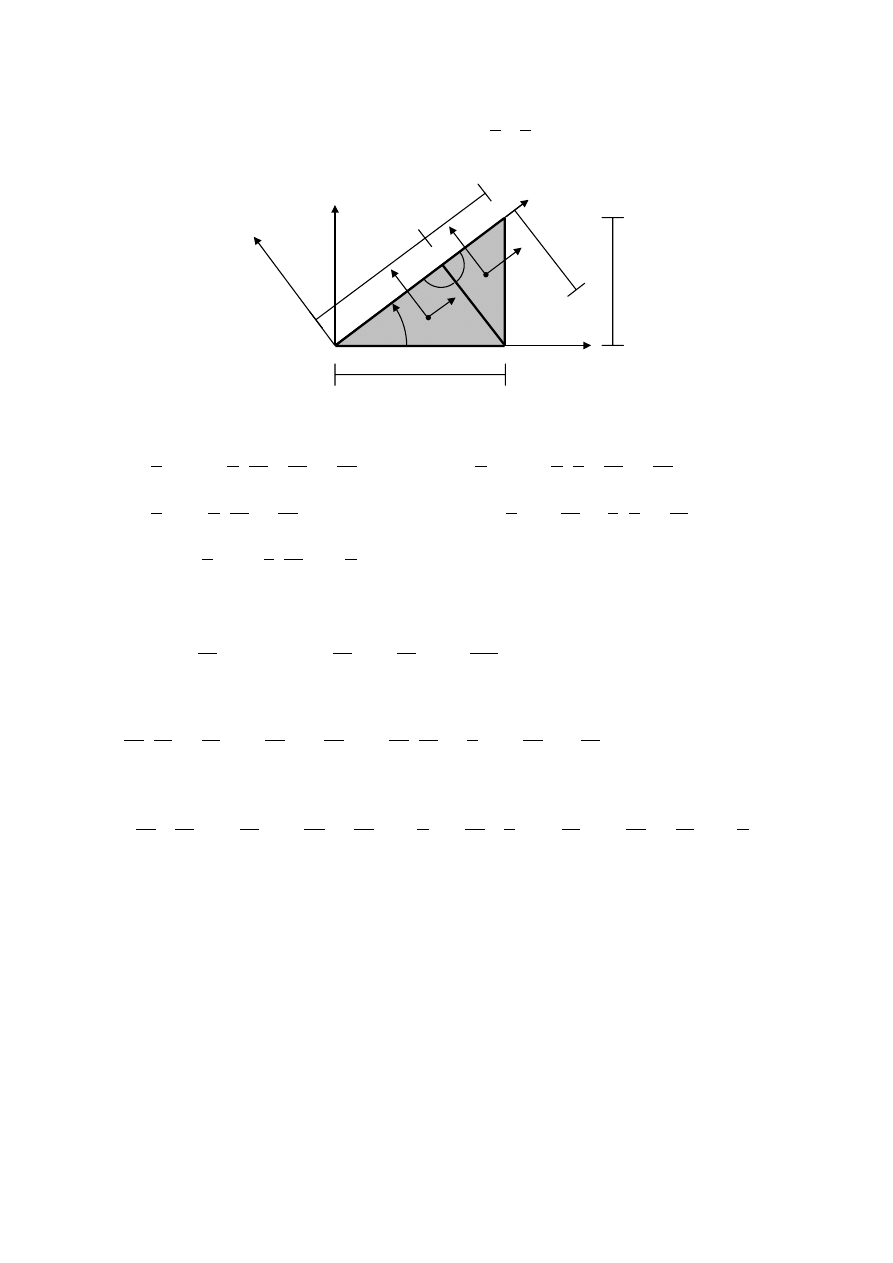
Momenty bezwładności i moment dewiacyjny trójkąta w obróconym układzie Ouv

możemy obliczyć bez konieczności transformowania ich przez obrót układu. Trójkąt można
podzielić na dwa trójkąty prostokątne, których boki przyprostokątne są równoległe do osi
układu Ouv zgodnie z poniższym rysunkiem.

5

3

=

α

sin

,

5

4

=

α

cos

r

r

α

sin

r

h

5

12

5

3

4

4

=

⋅

=

⋅

=

r

r

α

cos

r

b

5

16

5

4

4

4

2

=

⋅

=

⋅

=

3

r

r

α

sin

r

b

5

9

5

3

3

3

3

=

⋅

=

⋅

=

3r

h

4r

· ·

C

3

C

2

v

α

III

u

y

x

2

c

u

2

c

v

3

c

u

3

c

v

2

b

3

b

II

Pola powierzchni figury II i III oraz współrzędne ich środków ciężkości w obróconym

układzie Ouv wynoszą

2

2

II

25

96

5

12

5

16

2

1

2

1

r

r

r

h

b

A

=

⋅

⋅

=

⋅

⋅

=

,

2

3

III

25

54

5

12

5

9

2

1

2

1

r

r

r

h

b

A

=

⋅

⋅

=

⋅

⋅

=

r

r

b

u~

c

15

32

5

16

3

2

3

2

2

2

=

⋅

=

⋅

=

r

r

r

b

b

u~

c

5

19

5

9

3

1

5

16

3

1

3

2

3

=

⋅

+

=

⋅

+

=

r

r

h

v~

v~

c

c

5

4

5

12

3

1

3

1

3

2

−

=

⋅

−

=

⋅

−

=

=

Momenty bezwładności i moment dewiacyjny trójkąta, będącego sumą trójkątów II i

III, w obróconym układzie Ouv obliczymy jako sumy momentów dla figur składowych.

(

)

4

4

3

3

3

2

III

II

76

5

25

144

5

12

5

12

1

12

1

r

.

r

r

r

h

b

b

I

I

u

u

=

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

⋅

=

⋅

+

⋅

=

+

4

2

2

3

2

2

3

2

3

III

III

3

2

2

II

II

2

III

II

r

24

51

5

19

25

54

5

9

5

12

36

1

15

32

25

96

5

16

5

12

36

1

.

r

r

r

r

r

r

r

r

u~

A

I

u~

A

I

I

I

c

c

v

c

c

v

v

v

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

=

=

⋅

+

+

⋅

+

=

+

4

2

2

2

2

2

2

3

3

III

III

2

2

II

II

III

II

68

13

5

4

5

19

25

54

5

12

5

9

72

1

5

4

15

32

25

96

5

12

5

16

72

1

3

3

2

2

r

.

r

r

r

r

r

r

r

r

r

r

v~

u~

A

I

v~

u~

A

I

I

I

c

c

v

u

c

c

v

u

uv

uv

c

c

c

c

−

=

=

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛−

⋅

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

=

⋅

⋅

+

+

⋅

⋅

+

=

+

Momenty bezwładności i moment dewiacyjny rozważanej figury, będącej sumą figury

I, II i III w obróconym układzie Ouv obliczymy jako sumy momentów dla figur składowych.

4

4

4

III

II

I

664

21

76

5

904

15

r

.

r

.

r

.

I

I

I

I

u

u

u

u

=

+

=

+

+

=

4

4

4

III

II

I

144

67

24

51

904

15

r

.

r

.

r

.

I

I

I

I

v

v

v

v

=

+

=

+

+

=

4

4

4

III

II

I

555

3

68

13

125

10

r

.

r

.

r

.

I

I

I

I

uv

uv

uv

uv

−

=

−

=

+

+

=

.

Otrzymane wyniki są identyczne z uzyskanymi przy zastosowaniu podziału na dwie

figury składowe.

Osiowe momenty bezwładności oraz dewiacyjny moment figury względem osi

centralnych

wyznaczymy korzystając z przekształconych wzorów Steinera:

c

c

v

u

(

)

4

2

2

4

2

3140

20

3214

0

0686

13

664

21

r

.

r

.

r

.

r

.

v~

A

I

I

c

u

u

c

=

⋅

−

=

⋅

−

=

4

(

)

4

2

2

4

2

7763

17

9436

1

0686

13

144

67

r

.

r

.

r

.

r

.

u~

A

I

I

c

v

v

c

=

⋅

−

=

⋅

−

=

r

.

r

.

r

.

r

.

r

.

v~

u~

A

I

I

c

c

uv

v

u

c

c

4

2

4

7186

11

3214

0

9436

1

0686

13

555

3

−

=

⋅

⋅

−

−

=

⋅

⋅

−

=

.

Kąt φ

o

między osiami prostokątnego układu

i układu głównych osi bezwładności

spełnia równanie:

c

c

v

u

(

)

2356

9

7763

17

3140

20

7186

11

2

2

2

4

4

4

o

.

r

.

r

.

r

.

I

I

I

tg

c

c

c

c

v

u

v

u

=

−

−

⋅

−

=

−

−

=

ϕ

stąd

, a więc

.

rad

4629

1

2

o

.

=

ϕ

rad

7315

0

o

.

=

ϕ

Główna oś bezwładności, względem której moment bezwładności ma wartość

tworzy z osią

kąt

, natomiast główna oś bezwładności, względem której

moment bezwładności ma wartość

max

I

I

=

1

c

u

1

ϕ

min

I

I

=

2

tworzy z osią kąt

c

u

2

ϕ

.

c

u

I >

to

, a

c

v

I

rad

7315

0

o

1

.

=

ϕ

=

ϕ

rad

3023

2

rad

2

7315

0

2

o

2

.

.

=

⎟

⎠

⎞

⎜

⎝

⎛

π

+

=

π

+

ϕ

=

ϕ

Momenty bezwładności względem głównych osi bezwładności

osiągają wartości

ekstremalne:

c

c

v

u

(

)

4

2

4

2

4

4

4

4

2

2

1

8322

30

7186

11

2

7763

17

3140

20

2

7763

17

3140

20

2

2

r

.

r

.

r

.

r

.

r

.

r

.

I

I

I

I

I

I

I

c

c

c

c

c

c

v

u

v

u

v

u

max

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

(

)

4

2

4

2

4

4

4

4

2

2

2

2581

7

7186

11

2

7763

17

3140

20

2

7763

17

3140

20

2

2

r

.

r

.

r

.

r

.

r

.

r

.

I

I

I

I

I

I

I

c

c

c

c

c

c

v

u

v

u

v

u

min

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

Kierunek maksymalnego
momentu bezwładności

C

Kierunek minimalnego
momentu bezwładności

1

ϕ

2

ϕ

c

u

c

v

5

Przykład 2.4. Figura z dwiema osiami symetrii

Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury.

2a

2a

2a

2a

4a

4a

4a

4a

Dla rozważanej figury przyjmiemy dwa współśrodkowe układy współrzędnych xy oraz

ξη. Oba układy są układami centralnymi. Układ ξη jest ponadto układem osi głównych,
ponieważ osie ξ i η są osiami symetrii figury. Należy oczywiście ustalić, która z osi układu ξη
jest osią maksymalnego momentu bezwładności, a która osią minimalnego momentu
bezwładności.

x

η

y

ξ

C

2a

2a

2a

2a

4a

4a

4a

4a

x

y

I

II

C

III

2a

2a

4a

4a

Moment bezwładności rozpatrywanej figury względem osi x policzymy jako

podwojoną sumę momentów bezwładności figur składowych (figury I, II i III).

( )

( )

( )

4

3

3

3

312

2

2

12

1

2

4

3

1

6

2

3

1

2

a

a

a

a

a

a

a

I

x

=

⎥⎦

⎤

⎢⎣

⎡

⋅

⋅

+

⋅

⋅

+

⋅

⋅

⋅

=

Moment bezwładności figury względem osi y ma taką samą wartość.

4

312a

I

I

x

y

=

=

Wyznaczymy teraz moment bezwładności względem osi η, stosując nowy podział na

figury składowe. Figury II i IV traktujemy jako pola "ujemne". Momenty bezwładności figury
I i II mnożymy przez dwa, natomiast moment bezwładności figury IV mnożymy przez cztery.

η

6a

I

η

III

a

2

2

a

2

2

IV

a

2

a

2

II

4a

4a

η

6a

Centralny moment bezwładności kwadratu nie zależy od kierunku osi centralnej. Oś η

jest osią centralną dla kwadratu I, II i III.

( )

( )

(

)

(

) (

)

4

3

4

4

4

3

1

177

2

2

2

2

12

1

4

2

2

12

1

4

12

1

6

12

1

2

a

a

a

a

a

a

I

η

=

⋅

⋅

⋅

−

⋅

+

⎥⎦

⎤

⎢⎣

⎡

⋅

−

⋅

⋅

=

W dalszych obliczeniach wykorzystamy to, że suma momentów bezwładności

względem obu osi układów współśrodkowych jest stała.

η

ξ

y

x

I

I

I

I

+

=

+

czyli

4

4

4

3

2

446

3

1

177

312

2

2

a

a

a

I

I

I

I

I

I

η

x

η

y

x

ξ

=

−

⋅

=

−

⋅

=

−

+

=

Z porównania wartości głównych momentów bezwładności wynika, że oś ξ jest kierunkiem
maksymalnego momentu bezwładności a oś η jest kierunkiem minimalnego momentu
bezwładności.

4

2

3

1

177 a

I

I

I

min

η

=

=

=

,

4

1

3

2

446 a

I

I

I

max

ξ

=

=

=

x

ξ-kierunek maksymalnego
momentu bezwładności

C

η -kierunek minimalnego
momentu bezwładności

4

2

π

=

ϕ

4

1

π

−

=

ϕ

2

Przykład 2.5. Figura z dwiema osiami symetrii

Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury korzystając z metody analitycznej i graficznej (konstrukcja koła Mohra).

a

a

2a

2a

5a

5a

a

a

2a

2a

5a

5a

Dla rozważanej figury przyjmiemy dwa współśrodkowe układy współrzędnych xy oraz

ξη. Oba układy są układami centralnymi. Układ ξη jest ponadto układem osi głównych
ponieważ osie ξ i η są osiami symetrii figury. Należy oczywiście ustalić, która z osi układu ξη
jest osią maksymalnego momentu bezwładności, a która osią minimalnego momentu
bezwładności.

ξ

η

x

y

C

5a

5a

2a

2a

a

a

5a

5a

2a

2a

a

a

W celu wyznaczenia momentu bezwładności względem osi x dokonamy podziału
rozpatrywanej figury na figury składowe.

a

a

2a

2a

5a

5a

III

3

4

c

x

4

c

y

C

x

y

I

IV

4

C

4

c

x

4

c

y

C

II

5a

5a

2a

2a

a

a

Moment bezwładności rozpatrywanej figury względem osi x policzymy jako

podwojoną sumę momentów bezwładności względem osi x figur składowych (figury I, II, III i
IV). Moment bezwładności figury względem osi y ma taką samą wartość. W przypadku figury
IV należy zastosować twierdzenie Steinera. Pole powierzchni figury III i IV wynosi

2

IV

III

6

6

2

2

1

a

a

a

A

A

=

⋅

⋅

=

=

(

)

( )

( )

( )

( )

4

2

2

3

3

3

3

IV

III

II

I

6

1

248

6

3

1

2

6

6

2

36

1

2

6

12

1

2

2

3

1

3

3

12

1

2

2

a

a

a

a

a

a

a

a

a

a

a

a

I

I

I

I

I

I

x

x

x

x

y

x

=

=

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⋅

+

⋅

⋅

+

⋅

⋅

+

⋅

⋅

+

⋅

⋅

⋅

=

=

+

+

+

⋅

=

=

Dewiacyjny moment rozpatrywanej figury w układzie xy policzymy jako podwojoną

sumę momentów dewiacyjnych figur składowych (figury I, II, III i IV). W przypadku figury
III i IV należy zastosować twierdzenie Steinera. Momenty dewiacyjne tych dwóch figur w
układzie xy mają te same wartości, można więc w obliczeniach uwzględnić to, licząc
podwojoną wartość momentu dewiacyjnego np. dla figury III.

(

) (

)

( ) ( )

( ) ( )

( ) ( )

4

2

2

2

2

2

2

2

III

II

I

IV

III

II

I

4

1

57

6

3

1

2

2

3

1

6

6

2

72

1

2

2

2

4

1

3

3

24

1

2

2

2

2

a

a

a

a

a

a

a

a

a

a

a

I

I

I

I

I

I

I

I

xy

xy

xy

xy

xy

xy

xy

xy

−

=

=

⎭

⎬

⎫

⎩

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

⋅

+

⋅

⋅

+

⋅

−

⋅

⋅

=

=

⋅

+

+

⋅

=

+

+

+

⋅

=

Główna oś bezwładności, względem której moment bezwładności ma wartość

2

max

I

I

=

1

tworzy z osią x kąt

, natomiast główna oś bezwładności, względem której

moment bezwładności ma wartość

1

ϕ

min

I

I

=

2

tworzy z osią x kąt

2

ϕ

.

Ponieważ I

x

= I

y

, I

xy

< 0 to

4

1

π

=

ϕ

, natomiast

4

2

π

−

=

ϕ

.

Momenty bezwładności względem głównych centralnych osi bezwładności osiągają

wartości ekstremalne:

4

2

4

4

2

2

2

1

12

5

305

4

1

57

6

1

248

2

2

a

a

a

I

I

I

I

I

I

I

I

I

xy

x

xy

y

x

y

x

max

=

⎟

⎠

⎞

⎜

⎝

⎛−

+

=

+

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

4

2

4

4

2

2

2

2

12

11

190

4

1

57

6

1

248

2

2

a

a

a

I

I

I

I

I

I

I

I

I

xy

x

xy

y

x

y

x

min

=

⎟

⎠

⎞

⎜

⎝

⎛−

−

=

−

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

ξ - kierunek maksymalnego
momentu bezwładności

η - kierunek minimalnego
momentu bezwładności

x

4

1

π

=

ϕ

4

2

π

=

ϕ

C

Główne centralne momenty bezwładności możemy wyznaczyć w inny sposób.

III

a

2

2

3

a

2

2

3

a

2

3

a

2

3

η

a

2

2

a

2

4

I

II

η

η

3

Obliczymy wartość momentu bezwładności względem osi η, stosując nowy podział na

figury składowe. Figurę III traktujemy jako pole "ujemne". Momenty bezwładności figury I i
III mnożymy przez cztery.

(

)

( )

4

3

4

3

12

11

190

2

2

3

2

2

3

12

1

4

2

3

12

1

2

4

2

2

12

1

4

a

a

a

a

a

a

I

η

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

⋅

−

⋅

+

⋅

⋅

⋅

=

W dalszych obliczeniach wykorzystamy to, że suma momentów bezwładności

względem obu osi układów współśrodkowych jest stała.

η

ξ

y

x

I

I

I

I

+

=

+

czyli

4

4

4

12

5

305

12

11

190

6

1

248

2

2

a

a

a

I

I

I

I

I

I

η

x

η

y

x

ξ

=

−

⋅

=

−

⋅

=

−

+

=

Z porównania wartości głównych momentów bezwładności wynika, że oś

ξ jest

kierunkiem maksymalnego momentu bezwładności, a oś

η jest kierunkiem minimalnego

momentu bezwładności.

4

2

12

11

190

a

I

I

I

min

η

=

=

=

,

4

1

12

5

305

a

I

I

I

max

ξ

=

=

=

Główne centralne momenty bezwładności oraz kierunki główne można wyznaczyć metodą
graficzną, stosując konstrukcję koła Mohra. Korzystamy z wyznaczonych wartości
momentów bezwładności w układzie

xy

4

4

167

248

6

1

248

a

.

a

I

I

y

x

=

=

=

oraz wartości momentu dewiacyjnego

4

4

250

57

4

1

57

a

.

a

I

xy

−

=

−

=

.

Kolejność postępowania przy wyznaczaniu głównych momentów bezwładności i kierunków
głównych metodą graficzną jest następująca:
1. Wyznaczenie położenia punktów

A i B

Wartości momentów bezwładności w układzie

xy

stanowią odpowiednio

współrzędne punktów

A

4

167

248

a

.

I

I

y

x

=

=

(

)

0

167

248

4

,

a

.

I

x

=

i B

(

)

0

167

248

4

,

a

.

I

y

=

. W rozpatrywanym

zadaniu położenie punktów A

(

)

0

167

248

4

,

a

.

i B

(

)

0

167

248

4

,

a

.

jest wspólne.

2. Wyznaczenie położenia punktu C
Punkt C

(

)

(

)

0

167

248

5

0

4

,

a

.

I

I

.

y

x

=

+

⋅

, czyli C

(

)

0

167

248

4

,

a

.

, jest środkiem odcinka

AB i

środkiem koła Mohra. W rozpatrywanym zadaniu położenie punktów

C, A i B jest wspólne.

3. Wyznaczenie położenia punktu

D

Po uwzględnieniu wartości

oraz

otrzymamy współrzędne

4

167

248

a

.

I

x

=

4

250

57

a

.

I

xy

−

=

punktu

D

(

)

(

)

4

4

250

57

167

248

a

.

I

,

a

.

I

xy

x

−

−

=

−

=

, czyli

D

(

)

4

4

250

57

167

248

a

.

,

a

.

.

4. Wyznaczenie promienia koła Mohra
Łączymy punkty

C i D odcinkiem

CD

, który stanowi promień

R koła Mohra. Promieniem

tym zataczamy okrąg.
5. Wyznaczenie głównych momentów bezwładności
Koło Mohra przecina oś poziomą w dwu punktach:

E i F. Współrzędne tych punktów są

następujące:

E

(

)

0

917

190

4

,

a

.

,

F

(

)

0

417

305

4

,

a

.

. Długość odcinka

OE

odpowiada

minimalnemu momentowi bezwładności

, natomiast długość odcinka

2

I

F

O

odpowiada

maksymalnemu momentowi bezwładności .

1

I

6. Wyznaczenie kierunków głównych

4

Oś przechodząca przez punkty

E i D jest osią maksymalnego momentu bezwładności, a oś

przechodząca przez punkty

F i D jest osią minimalnego momentu bezwładności.

2

I

O

Momenty bezwładności

Moment

y dewiac

yj

ne

kierunek maksymalnego
momentu bezwładności

kierunek minimalnego
momentu bezwładności

Przyjęta skala: 50

r

4

1

I

E

2

y

x

y

x

I

I

=

=

I

I

+

A=B=C

D

F

R

4

2

π

−

=

ϕ

4

1

π

=

ϕ

(

)

( )

(

)

(

)

( )

0

0

0

2

0

0

1

2

,

I

F

,

I

E

I

,

I

D

,

I

I

C

,

I

B

,

I

A

xy

x

y

x

y

x

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

5

Przykład 2.6. Przekrój złożony z trzech kształtowników walcowanych.

Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższego przekroju złożonego z trzech kształtowników walcowanych.

120x80x10

240

80x80x10

Dane dotyczące kształtowników przyjęto wg: Mikołaj Żyburtowicz Konstrukcje stalowe,
WSiP, 1974.
Kształtownik I - ceownik [ 240

y

x

x

y

e

s

h

2

4

4

cm

3

42

cm

248

cm

3600

cm

23

2

e

mm

85

s

mm

240

h

.

F

I

I

.

y

x

=

=

=

=

=

=

Kształtownik II - kątownik nierównoramienny L 120x80x10

b

x

a

x

y

y

ξ

ξ

η

η

1

x

x

e

y

e

1

x

2

4

4

4

4

cm

2

19

cm

575

cm

7

57

cm

6

99

cm

279

cm

93

3

e

cm

96

1

e

mm

120

b

mm

80

a

1

.

F

I

.

I

.

I

I

.

.

x

η

y

x

x

y

=

=

=

=

=

=

=

=

=

Kształtownik III - kątownik równoramienny L 80x80x10

a

e

x

x

y

y

η

ξ

ξ

e

η

a

2

4

4

4

cm

1

15

cm

5

36

cm

140

cm

4

88

cm

35

2

e

mm

80

a

.

F

.

I

I

.

I

I

.

η

ξ

y

x

=

=

=

=

=

=

=

W tablicach do projektowania konstrukcji stalowych nie są podane wartości

momentów dewiacyjnych, których znajomość jest nieodzowna do wyznaczenia głównych
centralnych momentów bezwładności oraz kierunków głównych dla rozpatrywanego
przekroju złożonego. Moment dewiacyjny ceownika względem jego osi centralnych jest
równy zero, gdyż oś x jest osią symetrii przekroju. Momenty dewiacyjne obu kątowników w
układzie xy są różne od zera. W celu wyznaczenia momentu dewiacyjnego skorzystamy ze
wzorów na główne momenty bezwładności:

2

2

1

2

2

xy

y

x

y

x

max

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

2

2

2

2

2

xy

y

x

y

x

min

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

.

Po odjęciu stronami otrzymamy:

2

2

2

1

2

2

xy

y

x

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

=

−

.

Następnie po przekształceniu wzór na moment dewiacyjny przyjmie postać:

2

2

2

1

2

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

⎟

⎠

⎞

⎜

⎝

⎛ −

±

=

y

x

xy

I

I

I

I

I

.

W tablicach do projektowania konstrukcji stalowych kierunek maksymalnego

momentu bezwładności oznaczony jest przez ξ, natomiast kierunek minimalnego momentu
bezwładności oznaczony jest przez η. Uwzględniając to otrzymamy wzór:

2

2

2

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

±

=

y

x

η

ξ

xy

I

I

I

I

I

.

Wyznaczamy momenty dewiacyjne dla kątowników.

Kształtownik II - kątownik nierównoramienny L 120x80x10

W tablicach do projektowania konstrukcji stalowych podana jest tylko wartość

minimalnego momentu bezwładności

. W celu wyznaczenia wartości

skorzystamy z

zależności

η

I

ξ

I

η

ξ

y

x

I

I

I

I

+

=

+

,

czyli

η

y

x

ξ

I

I

I

I

−

+

=

.

2

Po podstawieniu wartości odczytanych z tablic otrzymamy

4

4

4

4

cm

9

320

cm

7

57

cm

6

99

cm

279

.

.

.

I

I

I

I

η

y

x

ξ

=

−

+

=

−

+

=

Wyznaczamy moment dewiacyjny

4

2

4

4

2

4

4

2

2

cm

29

96

2

cm

6

99

cm

279

2

cm

7

57

cm

9

320

2

2

.

.

.

.

I

I

I

I

I

y

x

η

ξ

xy

±

=

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

±

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

±

=

Znak momentu dewiacyjnego zależy od położenia kątownika nierównoramiennego w

stosunku do układu osi centralnych xy.

W rozpatrywanym przypadku w pierwszej i trzeciej ćwiartce układu współrzędnych, w

których iloczyn współrzędnych x·y jest dodatni, znajduje się większa część pola figury (na
powyższym rysunku są to ciemniejsze fragmenty figury). Na tej podstawie można stwierdzić,
że moment dewiacyjny kątownika nierównoramiennego jest dodatni.

4

cm

29

96.

I

xy

=

Kształtownik III - kątownik równoramienny L 80x80x10

W przypadku kątownika równoramiennego w tablicach podane są wartości obu

głównych centralnych momentów bezwładności

i . Poza tym

, a więc wzór na

moment dewiacyjny uprości się.

ξ

I

η

I

y

x

I

I

=

4

4

4

2

2

2

cm

75

51

2

cm

5

36

cm

140

2

2

2

2

.

.

I

I

I

I

I

I

I

I

I

η

ξ

η

ξ

y

x

η

ξ

xy

±

=

=

−

±

=

−

±

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

±

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

±

=

Znak momentu dewiacyjnego zależy od położenia kątownika równoramiennego w

stosunku do układu osi centralnych xy.

x

y

C

x

y

C

W rozpatrywanym przypadku w drugiej i czwartej ćwiartce układu współrzędnych, w

których iloczyn współrzędnych x·y jest ujemny, znajduje się większa część pola figury (na
powyższym rysunku są to ciemniejsze fragmenty figury). Na tej podstawie można stwierdzić,
że moment dewiacyjny kątownika równoramiennego jest ujemny.

4

cm

75

51.

I

xy

−

=

3

Dla przekroju złożonego z trzech kształtowników walcowanych przyjmujemy układ osi

Oxy.

II

I

III

x

1

C

y

O

1

c

x

3

c

x

3

c

y

1

c

y

2

c

x

2

c

y

2

C

3

C

4cm

8cm

8cm

0.5cm

12cm

8cm

12cm

8.5cm

12cm

W celu wyznaczenia współrzędnych środka ciężkości figury złożonej określamy pola

powierzchni i współrzędne środków ciężkości w układzie

Oxy dla figur składowych na

podstawie tablic do projektowania konstrukcji stalowych.

2

I

cm

3

42.

A

=

0

1

=

c

x~

cm

23

2

1

.

y~

c

−

=

2

II

cm

2

19.

A

=

(

)

cm

96

5

cm

96

1

4

2

.

.

x~

c

−

=

+

−

=

cm

93

3

2

.

y~

c

=

2

III

cm

1

15.

A

=

(

)

cm

35

14

cm

35

2

12

3

.

.

x~

c

=

+

=

(

)

cm

15

6

cm

35

2

5

8

3

.

.

.

y~

c

−

=

−

−

=

Pole powierzchni figury złożonej wynosi

2

2

2

2

III

II

I

cm

6

76

cm

1

15

cm

2

19

cm

3

42

.

.

.

.

A

A

A

A

=

+

+

=

+

+

=

Moment statyczny figury złożonej względem osi y wynosi

(

)

3

2

2

2

3

III

2

II

1

I

cm

253

102

cm

35

14

cm

1

15

cm

96

5

cm

2

19

0

cm

3

42

.

.

.

.

.

.

x~

A

x~

A

x~

A

S

c

c

c

y

=

⋅

+

−

⋅

+

⋅

=

=

⋅

+

⋅

+

⋅

=

Moment statyczny figury złożonej względem osi x wynosi

(

)

(

)

3

2

2

2

3

III

2

II

1

I

cm

738

111

cm

15

6

cm

1

15

cm

93

3

cm

2

19

cm

23

2

cm

3

42

.

.

.

.

.

.

.

y~

A

y~

A

y~

A

S

c

c

c

x

−

=

−

⋅

+

⋅

+

−

⋅

=

=

⋅

+

⋅

+

⋅

=

Współrzędne środka ciężkości figury złożonej są równe

cm

335

1

cm

6

76

cm

253

102

S

2

3

.

.

.

A

x~

y

c

=

=

=

cm

459

1

cm

6

76

cm

738

111

S

2

3

.

.

.

A

y~

x

c

−

=

−

=

=

Moment bezwładności figury złożonej względem osi x wynosi

(

)

(

)

4

2

2

4

4

2

2

4

2

3

III

III

II

2

1

I

I

III

II

I

cm

9

1692

cm

15

6

cm

1

15

cm

4

88

cm

575

cm

23

2

cm

3

42

cm

248

3

1

.

.

.

.

.

.

y~

A

I

I

y~

A

I

I

I

I

I

c

x

x

c

x

x

x

x

x

c

c

=

−

⋅

+

+

+

−

⋅

+

=

=

⋅

+

+

+

⋅

+

=

+

+

=

Moment bezwładności figury złożonej względem osi y wynosi

(

)

(

)

4

2

2

4

2

2

4

4

2

3

III

III

2

2

II

II

I

III

II

I

cm

4

7579

cm

35

14

cm

1

15

cm

4

88

cm

96

5

cm

2

19

cm

6

99

cm

3600

3

2

.

.

.

.

.

.

.

x~

A

I

x~

A

I

I

I

I

I

I

c

y

c

y

y

y

y

y

y

c

c

=

⋅

+

+

−

⋅

+

+

=

=

⋅

+

+

⋅

+

+

=

+

+

=

Moment dewiacyjny figury złożonej w układzie xy wynosi

(

)

(

)

4

2

4

2

4

3

3

III

III

2

2

II

II

I

III

II

I

cm

8

1737

cm

15

6

cm

35

14

cm

1

15

cm

75

51

cm

93

3

cm

96

5

cm

2

19

cm

29

96

0

3

3

2

2

.

.

.

.

.

.

.

.

.

y~

x~

A

I

y~

x~

A

I

I

I

I

I

I

c

c

y

x

c

c

y

x

xy

xy

xy

xy

xy

c

c

c

c

−

=

=

−

⋅

⋅

+

−

⋅

−

⋅

+

+

=

=

⋅

⋅

+

+

⋅

⋅

+

+

=

+

+

=

4

Znając wartości momentów bezwładności i momentu dewiacyjnego figury złożonej w

układzie

Oxy możemy korzystając z twierdzenia Steinera wyznaczyć momenty bezwładności

i moment dewiacyjny w układzie osi centralnych

.

c

c

y

x

(

)

4

2

2

4

2

cm

8

1529

cm

459

1

cm

6

76

cm

9

1692

.

.

.

.

y~

A

I

I

c

x

x

c

=

−

⋅

−

=

⋅

−

=

(

)

4

2

2

4

2

cm

9

7442

cm

335

1

cm

6

76

cm

4

7579

.

.

.

.

x~

A

I

I

c

y

y

c

=

⋅

−

=

⋅

−

=

(

)

4

2

4

cm

6

1588

cm

459

1

cm

335

1

cm

6

76

cm

8

1737

.

.

.

.

.

y~

x~

A

I

I

c

c

xy

y

x

c

c

−

=

−

⋅

⋅

−

−

=

⋅

⋅

−

=

.

Momenty bezwładności względem głównych centralnych osi bezwładności przyjmują

wartości:

(

)

4

2

4

2

4

4

4

4

2

2

1

cm

7

7842

cm

6

1588

2

cm

9

7442

cm

8

1529

2

cm

9

7442

cm

8

1529

2

2

.

.

.

.

.

.

I

I

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

max

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

(

)

4

2

4

2

4

4

4

4

2

2

2

cm

0

1130

cm

6

1588

2

cm

9

7442

cm

8

1529

2

cm

9

7442

cm

8

1529

2

2

.

.

.

.

.

.

I

I

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

min

=

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

Kąt φ

o

między osiami prostokątnego układu

i układu głównych osi bezwładności

spełnia równanie:

c

c

y

x

(

)

5373

0

cm

9

7442

cm

8

1529

cm

6

1588

2

2

2

4

4

4

o

.

.

.

.

I

I

I

tg

c

c

c

c

y

x

y

x

−

=

−

−

⋅

−

=

−

−

=

ϕ

stąd

,

.

rad

4930

0

2

o

.

−

=

ϕ

rad

2465

0

o

.

−

=

ϕ

Główna oś bezwładności, względem której moment bezwładności ma wartość

tworzy z osią

kąt

, natomiast główna oś bezwładności, względem której

moment bezwładności ma wartość

max

I

I

=

1

c

x

1

ϕ

min

I

I

=

2

tworzy z osią kąt

c

x

2

ϕ

.

Ponieważ

<

to kąt

c

x

I

c

y

I

rad

3243

1

rad

2

2465

0

2

o

1

.

π

.

=

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

π

+

ϕ

=

ϕ

, natomiast kąt

.

rad

2456

0

o

2

.

−

=

ϕ

=

ϕ

x

y

O

C

y

c

x

c

kierunek maksymalnego
momentu bezwładności

kierunek minimalnego
momentu bezwładności

1

ϕ

2

ϕ

5

Przykład 2.7. Przekrój złożony z dwuteownika i płaskowników.

Polecenie: Dobrać grubość g płaskownika o szerokości 90mm tak, aby moment bezwładności

figury złożonej był co najmniej dwa razy większy od momentu bezwładności względem

osi x dla dwuteownika .

x

I

Wyznaczyć przyrost momentów bezwładności

,

oraz pola powierzchni figury złożonej

F w stosunku do charakterystyk geometrycznych dwuteownika.

x

I

y

I

240

240

g

240mm

g

90mm

x

x

y

y

240

x

x

y

y

2

4

4

cm

1

46

cm

221

cm

4250

.

F

I

I

y

x

=

=

=

Dane dotyczące dwuteownika oraz płaskownika przyjęto wg: Władysław Bogucki, Mikołaj
Żyburtowicz Tablice do projektowania konstrukcji metalowych. Wyd. V, "Arkady" 1984, s.
20, 73.

Moment bezwładności względem osi x dla przekroju złożonego wynosi

4

2

3

4

cm

4250

2

2

1

cm

12

cm

9

cm

9

12

1

2

cm

4250

⋅

≥

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⋅

⋅

+

⋅

⋅

⋅

+

=

g

g

g

I

x

Po przekształceniu otrzymujemy nierówność w postaci

0

cm

4250

cm

2592

cm

216

cm

6

4

3

2

2

3

≥

−

⋅

+

⋅

+

⋅

g

g

g

,

która spełniona jest dla g≥1.4559cm.

Płaskowniki o szerokości 90mm są dostępne w następujących grubościach: 6, 8, 10,

12, 14, 16, 20, 25, 30 i 40mm. Najmniejsza grubość płaskownika spełniająca warunek
g≥1.4559cm wynosi 16mm=1.6cm. Wartości momentów bezwładności i pola przekroju
poprzecznego złożonego wynoszą

(

)

4

4

4

2

3

4

cm

8974

cm

4724

cm

4250

cm

6

1

2

1

cm

12

cm

6

1

cm

9

cm

6

1

cm

9

12

1

2

cm

4250

=

+

=

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

⋅

⋅

+

⋅

⋅

⋅

+

=

.

.

.

I

x

(

)

4

4

4

3

4

cm

4

415

cm

4

194

cm

221

cm

9

cm

6

1

12

1

2

cm

221

.

.

.

I

y

=

+

=

⋅

⋅

⋅

+

=

2

2

2

2

cm

9

74

cm

8

28

cm

1

46

cm

9

cm

6

1

2

cm

1

46

.

.

.

.

.

F

=

+

=

⋅

⋅

+

=

Przyrosty momentów bezwładności

,

oraz pola powierzchni figury złożonej F w

stosunku do charakterystyk geometrycznych dwuteownika są równe:

x

I

y

I

4

cm

4724

=

∆

x

I

4

cm

4

194.

I

y

=

∆

2

cm

8

28.

F

=

∆

Przyrosty względne momentów bezwładności ,

oraz pola powierzchni figury złożonej F

w stosunku do dwuteownika są równe:

x

I

y

I

%

%

I

I

x

x

111

100

cm

4250

cm

4724

4

4

=

⋅

=

∆

%

%

.

I

I

y

y

88

100

cm

221

cm

4

194

4

4

=

⋅

=

∆

%

%

.

.

F

F

62

100

cm

1

46

cm

8

28

2

2

=

⋅

=

∆

.

Z porównania wartości przyrostów momentów bezwładności przekroju złożonego

oraz

widać, że momenty bezwładności zwiększają się

znacznie, gdy duża część pola przekroju znajdzie się możliwie daleko od osi, względem której
jest obliczony moment.

4

cm

4724

=

∆

x

I

4

cm

4

194.

I

y

=

∆

2