//wmii.uwm.edu.pl/~germaniuk adres strony internetowej

Literatura.

W. Krysicki J. Bartos Rachunek prawdopodobieństwa i statystyka matematyczna w

Zadaniach.

Część I Rachunek prawdopodobieństwa

Część II Statystyka matematyczna

Wojciech Kordecki Rachunek prawdopodobieństwa i statystyka matematyczna

Definicje, twierdzenia, wzory.

Elementy statystyki opisowej.

Statystyka matematyczna zajmuje się analizą i opisem dużych zbiorowości i zjawisk masowych przy pomocy metod rachunku prawdopodobieństwa. Badaniu podlega pewien zbiór elementów ze względu na jedną lub więcej cech, który oznaczać będziemy przez Ζ . Zbiór Ζ posiadający przynajmniej jedną cechę wspólną dla wszystkich jego elementów i własność ze względu na którą elementy tego zbioru różnią się między sobą nazywamy populacją generalną.

Badaniu mogą podlegać wszystkie elementy zbioru Ζ / badanie kompletne / lub jego część / badanie częściowe /. Badanie kompletnie w większości nie jest możliwe / zbiór jest nieskończony, badanie jest pracochłonne, niszczy badane elementy / dlatego statystyka matematyczna zajmuje się głównie wnioskowaniem o całej zbiorowości na podstawie informacji uzyskanych z pewnego skończonego podzbioru ß zboru Ζ . Ten skończony zbiór będziemy nazywać próbą. Aby próba wiernie reprezentowała populację generalną Ζ to każdy element tej populacji powinien mieć jednakowe prawdopodobieństwo trafienia do próby. Taką próbę nazywamy próbą losową prosta.

Badaniu może podlegać jedna cecha lub więcej cech elementów populacji generalnej.

Na początek zajmiemy się badaniem jednej cechy. Badane cechy mogą być mierzalne wyrażane za pomocą liczby i niemierzalne / odcień barwy, kolor włosów, płeć, zawód …. /. W praktyce cechą niemierzalnym przyporządkowuje się liczby. Cechy mierzalne mogą być typu ciągłego / wartości cechy mogą przyjąć wszystkie liczby z określonego przedziału / i typu skokowego / wszystkich wartości cechy jest skończona lub przeliczalną ilość /.

Statystyka opisowa zajmuje się wstępnym opisem próby bez posługiwania się rachunku prawdopodobieństwa.

Szereg rozdzielczy.

Niech
będą wartościami cechy n - elementowej próby.

Przy większej liczebności próby (n > 30 ) w celu ułatwienia analizy próbę grupuje się w klasy tj. przedziały najczęściej jednakowej długości przyjmując uproszczenie, że wszystkie wartości należące do klasy mają wartość równą wartości środka przedziału. Następnie oblicza się liczebności przedziałów tzn. liczby - ilość elementów próby które maję wartości cechy z określonego przedziału. Ustalenie tych elementów tworzy szereg rozdzielczy danych próby.

Próba nie przedstawiona za pomocą szeregu rozdzielczego nazywamy próbą nieuporządkowaną /danymi nieuporządkowanymi /.

Istnieje kilka reguł ustalenia orientacyjnego liczby klas k i długości przedziału. Liczba klas nie może być za mała / traci się szczegóły danych / i nie za duża / traci się przejrzystość danych /.

Oblicza się tzw. rozstęp danych
gdzie
jest odpowiednio największą i najmniejszą wartością cechy w próbie.

Liczba klas
lub można odczytać z tabeli

Liczba pomiarów n	Liczba klas k
30 - 60	6 - 8
60 - 100	7 - 10
100 - 200	9 - 12
200 - 500	11 - 17
500 - 1500	16 - 25

Długość przedziału przyjmuje się
z nadmiarem tak aby

Punkty stanowiące granice poszczególnych klas ustala się z dokładnością
gdzie
jest dokładnością pomiaru wartości cechy w próbie.

Po ustaleniu tych elementów tworzy się szereg rozdzielczy próby.

Przedziały	Liczebność	Środki	Częstość	Łamana rozkładu
Klasowe cechy	klasy	klas	cechy w klasie	empirycznego
..	.	.	.	.
..	.	.	.	.

liczebność próby

długość przedziału klasowego

liczba przedziałów klasowych

końce i - tego przedziału klasowego

Stąd pole zawarte między łamaną łączącą punkty o współrzędnych
,
, ……….. ,
,
a osią OX jest równe 1 .

Analogicznie wartości
określają empiryczne wartości prawdopodobieństwa zdarzenia - wartość cechy elementu wylosowanego z populacji generalnej będzie należała do i - tego przedziału klasowego. Wartości te wraz ze wzrostem liczby n do nieskończoności dążą do wartości teoretycznych całej populacji generalnej.

Parametry opisowe próby obliczane za pomocą szeregu rozdzielczego.

Średnia arytmetyczna

Wartości
i = 1,2,….,k to środki przedziałów klasowych. Wartość
w przybliżeniu równa się średniej arytmetycznej z wartości cechy próby nieuporządkowanej. Ponadto
i
. Ostania własność jest prawdziwa wtedy i tyko wtedy gdy od wartości
odejmujemy wartość
.

Wariancja

Jest to średni rozrzut w kwadracie wartości cechy w próbie względem średniej arytmetycznej
.

Odchylenie standardowe

Jest to średni rozrzut wartości cechy w próbie względem średniej arytmetycznej

Mniejsza wariancja i odchylenie standardowe - rozrzut wartości cechy mniejsze a skupienie większe i odwrotnie większa wariancja i odchylenie standardowe - rozrzut wartości cechy większy a skupienie mniejsze. Wariancja i odchylenie jest miarą rozrzutu wartości cechy w próbie względem średniej arytmetycznej
.

Mediana czyli wartość środkowa.

Z szeregu rozdzielczego wartość środkową cechy oblicza się za pomocą wzoru:

gdzie indeks
to numer klasy zawierająca wartość środkową próby nieuporządkowanej.

Moda czyli dominanta

Modę czyli wartość dominującą w próbie z szeregu rozdzielczego oblicza się wzorem:

gdzie indeks
to numer klasy najliczniejszej.

Moment centralny
rzędu

Współczynnik asymetrii / skośności /

Jest miarą odstępstwa od symetrii wartości cechy w próbie. Dla
dane są symetryczne względem wartości
. Gdy
to antysymetria występuje w lewą stronę. Gdy
to antysymetria jest w prawą stronę.

Współczynnik spłaszczenia / eksces /

Jest miarą odstępstwa wartości cechy w próbie od rozkładu normalnego w pionie. / rozkład ten będzie zdefiniowany w dalszej wykładu /. W rozkładzie normalnym
i
.

Przykład
W badaniu rzeczywistego czasu przebywania cząstek reagentów
w reaktorze przepływowym doświadczalnie stosując metodę typu
sygnał /odpowiednio dobrana substancja, zwana traserem / --
odpowiedz, uzyskano następujące wyniki / w d /
4,6	5,5	5		4,9		3,9		4,3	4,3		3,7		4,5		4,6		4,2	5,3		5,3		3,8	4	4
3,9	2,7	3,3		6,2		5,4		4,5	5,9		8,3		3,3		6		3,8	6,1		3,2		3,9	6,1	4,5
6,2	5,3	5,7		5,1		5,4		6,3	4,7		5,2		4,8		4,4		4,3	6		3,7		3,7	5,1	4,7
5,3	5,7	5,4		6,6		5,5		4,6	5,2		4,6		5,9		4,3		5,3	4,6		4,7		5,3	6,5	3,7
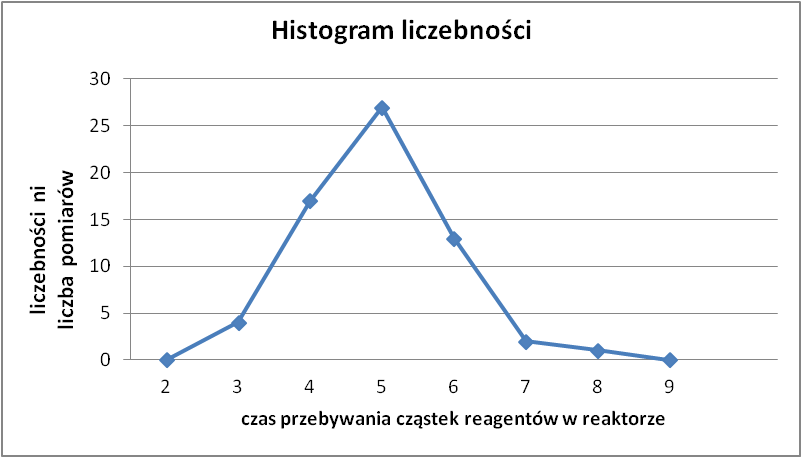
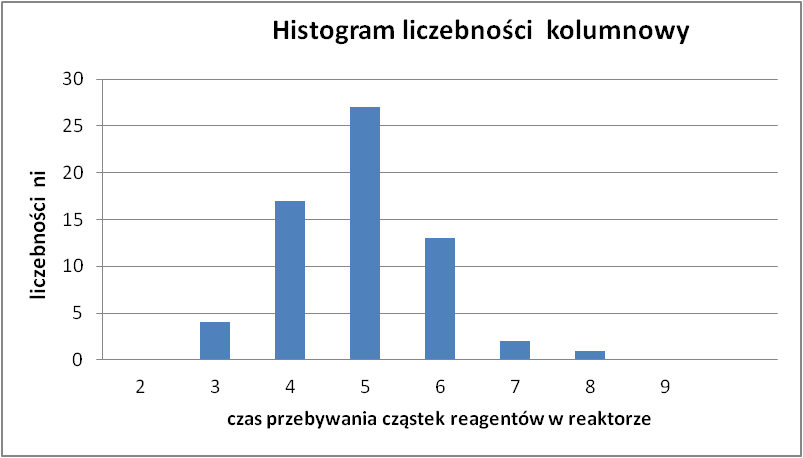
a) Określić populację generalną i rodzaj cechy oraz utworzyć szereg rozdzielczy. b). Podać interpretację danych /utworzyć histogram danych/
c). Obliczyć podstawowe parametry próby / średnią arytmetyczną ,wariancją,…./ Ad a),b)….

Elementem populacji generalnej jest doświadczenie badające rzeczywisty czas przebywania

cząstek reagentów w reaktorze przepływowym. Doświadczeń można przeprowadzić nieskończenie wiele a więc populacja jest nieskończona. Cecha - czas przebywania reagentów wyrażona w dniach jest typu ciągłego ponieważ można uzyskać każdą wartość z przedziału np. 2 do 10. Dokładność pomiaru α = 0,1 dnia.

= 8,3 - 2,7 = 5,6 . Dla liczby klas k = 7, 8 ,9.

Długość przedziału
∼ 0,8 ; 0,7 ; 0,62

Dla k = 6
∼ 0,9333 a więc decydując się na k = 6 i
mamy najlepsze przybliżenie z nadmiarem długości przedziału klasowego i przyzwoitą długość.

Skrajny lewy koniec przedziału klasowego
przyjmujemy 2,5.

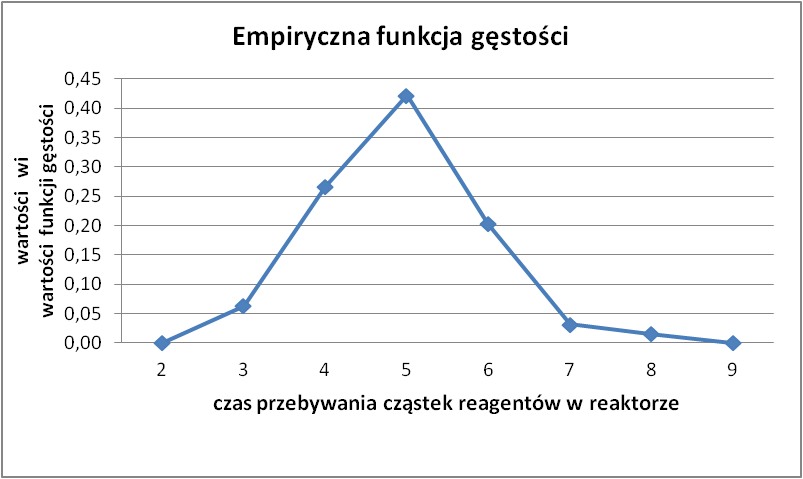
czas przebywania			liczba	środki		Częstość	funkcja
reagentów /w d /			pomiarów	przedziałów		przedziału	gęstości
2,5	3,5		4	3		0,063	0,06
3,5	4,5		17	4		0,266	0,27
4,5	5,5		27	5		0,422	0,42
5,5	6,5		13	6		0,203	0,20
6,5	7,5		2	7		0,031	0,03
7,5	8,5		1	8		0,016	0,02
	n =		64
			długość przedziału klasowego

Ad c).

czas przebywania regentów / w d /		Liczba pomiarów	środki przedziałów	składniki	składniki	składniki	składniki	składniki
2,5	3,5	4	3	12	14,77	36	-28,39	54,57
3,5	4,5	17	4	68	14,45	272	-13,32	12,28
4,5	5,5	27	5	135	0,16	675	0,01	0
5,5	6,5	13	6	78	15,11	468	16,29	17,56
6,5	7,5	2	7	14	8,64	98	17,95	37,3
7,5	8,5	1	8	8	9,47	64	29,16	89,77
	n =	64		315	62,61	1613	21,7	211,49

Średnia arytmetyczna
=
= 4,92 / z próby nieuporządkowanej
= 4,89 /

Wariancja sp. I
=
= 0,98 / z próby nieuporządkowanej
= 0,98 /

Wariancja sp. II
=
= 0,98

Odchylenie standardowe
=
= 0,99

Wartość środkowa należy do 3 - go przedziału stąd indeks w wzorze na medianę
= 3

Mediana
=
= 4,91

Najliczniejszy przedział ma indeks
= 3 stąd

Moda (dominanta)
=
= 4,83

Moment centralny 3 - go rzędu
=
= 0,34

Współczynnik asymetrii / skośności /
= 0,35

Moment centralny 4 - go rzędu
=
= 3,3045

Współczynnik spłaszczenia / eksces /
= 0,4

Parametry opisowe z próby nieuporządkowanej

Niech
będą wartościami cechy n - elementowej próby nieuporządkowanej.

Średnia arytmetyczna

i
. Ostania własność jest prawdziwa wtedy i tyko wtedy gdy od wartości
odejmujemy wartość
.

Wariancja

Jest to średni rozrzut w kwadracie wartości cechy w próbie względem średniej arytmetycznej
.

Odchylenie standardowe

Jest to średni rozrzut wartości cechy w próbie względem średniej arytmetycznej

Mniejsza wariancja i odchylenie standardowe - rozrzut wartości cechy mniejsze a skupienie większe i odwrotnie większa wariancja i odchylenie standardowe - rozrzut wartości cechy większy a skupienie mniejsze. Wariancja i odchylenie jest miarą rozrzutu wartości cech w próbie względem średniej arytmetycznej
.

Mediana czyli wartość środkowa.

Z szeregu rozdzielczego wartość środkową cechy oblicza się za pomocą wzoru:

Gdzie
dane próby nieuporządkowanej ustawione w kolejności rosnącej.

Moda czyli dominanta

Modę czyli wartość dominującą w próbie jest to wartość najczęściej występująca w próbie

Moment centralny
rzędu

Współczynnik asymetrii / skośności /

Jest miarą odstępstwa od symetrii wartości cechy w próbie. Dla
dane są symetryczne względem wartości
. Gdy
to antysymetria występuje w lewą stronę. Gdy
to antysymetria jest w prawą stronę.

Współczynnik spłaszczenia / eksces /

Jest miarą odstępstwa wartości cechy w próbie od rozkładu normalnego w pionie. / rozkład ten będzie zdefiniowany w dalszej wykładu /. W rozkładzie normalnym
i
.

Przykład

Badano wpływ preparatu jodowego na nieśność kur. Z populacji kur wybrano grupę doświadczalną której podano ten preparat. Liczba jaj zniesionych w okresie zimowym była następująca: 78 , 123 , 70 ,84 ,80.

a). Określić typ danych, elementy populacji generalnej i typ cechy.

b). Obliczyć podstawowe parametry próby.

Ad. a).

Dane próby są nieuporządkowane ponieważ nie możemy utworzyć szeregu rozdzielczego (n=5<30). Elementem badanej populacji generalnej jest kura której podaje się preparat jodowy których może w czasie być nieskończenie wiele a więc zbiór badanej populacji generalnej jest nieskończony. Cecha - liczba jaj zniesionych w okresie zimowym przez kurę z tej populacji jest typu skokowego (dyskretnego) i wartości jest przeliczalna ilość / nie możemy wykluczyć 1000 jaj ale z prawdopodobieństwem prawie zerowym lub zerowym /.

Ad. b).

Średnia arytmetyczna

Wariancja

Sposób II.

Odchylenie standardowe

Mediana czyli wartość środkowa.

Pozostałe podane parametry dla tak małej próby nie mają większego znaczeni.

---