Piotr Zaszkowski

Laboratorium Fizyczne

Ćwiczenie nr 2a.

Temat: Pomiar przyspieszenia ziemskiego za pomocą różnicowego wahadła matematycznego.

Teoria zjawiska:

Przez ciężar ciała rozumiemy siłę z jaką Ziemia przyciąga dane ciało. Siła ta nadaje swobodnie spadającemu ciału przyspieszenie g zwane przyspieszeniem ziemskim. Wartość tej siły można przedstawić wzorem: F = mg.

Wartość przyspieszenia ziemskiego nie jest stała, ale zależy od położenia punktu na powierzchni Ziemi. Przyczynami tego zjawiska są: a) spłaszczenie kuli ziemskiej, b) ruch obrotowy Ziemi, c) niejednorodność budowy Ziemi.

Jak wiadomo Ziemia ma kształt zbliżony do elipsoidy obrotowej, spłaszczonej od strony biegunów geograficznych, w skutek tego wartość g zależy od szerokości geograficznej i jest największa na biegunie, a najmniejsza na równiku.

Ruch obrotowy Ziemi powoduje powstanie siły odśrodkowej, która zmniejsza ciężar każdego ciała znajdującego się na Ziemi. Siła odśrodkowa jest prostopadła do osi ziemskiej, a więc jej kierunek względem poziomu zależy od szerokości geograficznej. Zmniejszenie ciężaru ciała jest największe na równiku i w miarę zbliżania się do bieguna maleje do zera.

Wartość g zmienia się w skutek działania tych dwóch czynników od wartości ok. 9,78m/s² na równiku do ok. 9,83m/s² na biegunie.

Niejednorodność budowy Ziemi, jak i również ukształtowanie powierzchni Ziemi powodują niewielkie lokalne wahania wartości g.

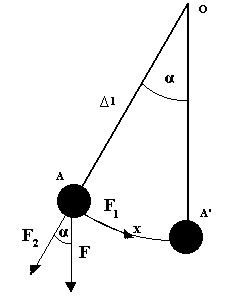
Wahadłem matematycznym nazywamy punkt materialny zawieszony na nieważkiej i nierozciągliwej nici, wykonujący drgania w płaszczyźnie pionowej. Siłę ciężkości działającą na ten punkt materialny rozkładamy na dwie składowe - równoległą i prostopadłą do nici ( tak jak zostało to pokazane na poniższym rysunku ). Składowa równoległą jest zrównoważona przez siłę naciągu nici, natomiast składowa prostopadła jest bezpośrednią przyczyną drgań tego wahadła.

Ruchem harmonicznym nazywamy taki ruch drgający, w którym siła jest wprost proporcjonalna do wychylenia i zwrócona ku środkowi drgań.

F = -4π²mx/T² gdzie x - wychylenie

Wyprowadzenie wzoru roboczego:

Z powyższego wzoru widać jasno, że siła powodująca ruch wahadła jest siłą wprost proporcjonalną do wychylenia, z czego wynika, że ruch wahadła dla małych wychyleń można uznać za harmoniczny.

Ponieważ g i l są wielkościami stałymi, równanie to wyraża zasadniczą cechę dynamiczną ruchu harmonicznego: przyspieszenie jest proporcjonalne do wychylenia.

F = 4π²mx/T² = mg x/Δl

Po przyrównaniu powyższych wartości otrzymujemy: g = 4π²( l₂ -l₁ )/ΔT² gdzie ΔT = T₂ - T₁.

Obliczenia do wykonanych pomiarów:

Przyspieszenie ziemskie (według obliczeń) wynosi:

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla l₁ i l₂:

Niepewność całkowita dla T₁:

Niepewność całkowita dla T₂:

Wartości pochodnych cząstkowych :

Podstawiając wszystkie wartości otrzymujemy:

Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wynik pomiaru:

Wnioski:

Dzięki wahadłom matematycznym można dość precyzyjnie wyznaczyć wartość przyspieszenia ziemskiego. Podczas przeprowadzania doświadczenia należy pamiętać, aby ruch wahadła odbywał się po torze prostym, a nie po okręgu. Dlatego też kąt wychylenia wahadła powinien być niewielki.

F = mg

F₁ = F sinα

sinα = łuk AA'/Δl

dla małych kątów można przyjąć łuk AA' = x

gdzie x - prosta łącząca punkty A i A'

wówczas:

F₁ = mg x/Δl gdzie Δl = l₂ - l₁

---