Uniwersytet Zielonogórski		SPRAWOZDANIE Z ĆWICZENIA
	Instytut Fizyki
			TEMAT: Wyznaczanie długości fali świetlnej przy pomocy siatki dyfrakcyjnej
Wydział Mechaniczny
			Data		ZALICZENIE
			Nr ćw.

Sprawozdanie pobrane ze StudentSite.pl
Chcesz więcej? Wejdź na: http://www.studentsite.pl/materialy_studenckie.html
Możesz także wspomóc swoimi sprawozdaniami innych: http://www.studentsite.pl/panel_materialy_studenckie/add

OBOWIĄZUJACY ZAKRES MATERIAŁU:

1. Widmo fal elektromagnetycznych. Własności fal elektromagnetycznych. Fale świetlne.

2. Widma emisyjne i absorpcyjne. Zjawisko pochłaniania światła.

3. Zjawisko odbicia i załamania światła. Prawa Snelliusa.

4. Zjawisko interferencji i dyfrakcji światła. Doświadczenie Younga.

5. Dualizm korpuskularno - falowy światła. Kwant światła, energia kwantu.

6. Przyrządy spektralne: spektografy, spektrometry. Siatka dyfrakcyjna i jej zastosowanie.

LITERATURA:

1. Jerzy Massalski, Michalina Massalska - FIZYKA dla inżynierów część I Fizyka Klasyczna.

2. "Słownik fizyczny" - Wiedza Powszechna, Warszawa 1984

3. PORADNIK INŻYNIERA - mechanika tom pierwszy, Wydawnictwo Naukowo - Techniczne Warszawa.

4. Czesław Bobrowski Fizyki - krótki kurs dla inżynierów.

1. Wstęp teoretyczny

1. Widmo fal elektromagnetycznych. Własności fal elektromagnetycznych. Fale świetlne.

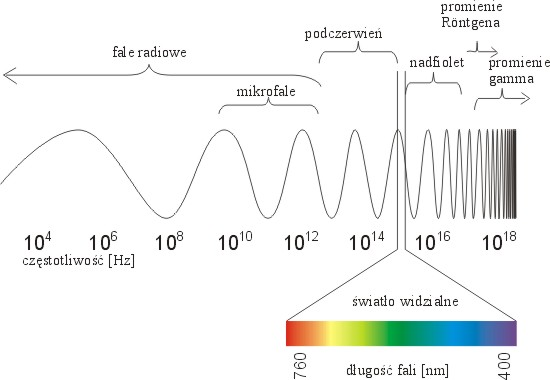
Fale elektromagnetyczne można podzielić ze względu na częstotliwość lub długość, taki podział nazywa się widmem fal elektromagnetycznych. Obejmuje ono fale radiowe, mikrofale, promieniowanie podczerwone, światło widzialne, promieniowanie nadfioletowe, promieniowanie rentgenowskie, promieniowania gamma.

Zakresy poszczególnych rodzajów promieniowania nie mają wyraźnych i ostrych granic. Niektóre z nich wzajemnie zachodzą na siebie. Dzieje się tak np. w zakresie promieniowania nadfioletowego i rentgenowskiego czy też promieniowania podczerwonego i promieniowania radiowego.

Fale elektromagnetyczne wypełniają otaczającą nas przestrzeń, my jednak zauważamy jedynie fale z małego zakresu widma tzw. światło widzialne. Promieniowanie elektromagnetyczne rozchodząc się objawia swe własności falowe zachowując się jak każda fala, ulega interferencji, dyfrakcji, spełnia prawo odbicia i załamania.

Rozchodzenie się fali w ośrodkach silnie zależy od ośrodków oraz częstotliwości fali. Fala rozchodząc się w ośrodku pobudza do drgań cząsteczki, atomy i elektrony zawarte w ośrodku, które są źródłami fal wtórnych, zmieniając tym samym warunki rozchodzenia się fali w stosunku do próżni.

Powstawanie i pochłanianie promieniowania elektromagnetycznego wiąże się ze zmianą ruchu ładunku elektrycznego.

Własności promieniowania elektromagnetycznego silnie zależą od długości fali (częstotliwości promieniowania) i dlatego dokonano podziału promieniowania elektromagnetycznego ze względu na jego częstotliwość.

Właściwości fal elektromagnetycznych:

- fale elektromagnetyczne emiotowane są z nadajnika, a odbierane przez odbiornik.

- przechodzą przez izolatory, a nie przechodzą przez przewodniki.

- podlegają zjawisku odbicia zgodnie z prawem odbicia,

- jest falą poprzeczną

- ulegają zjawisku dyfrakcji, interferencji i polaryzacji,

2. Widma emisyjne i absorpcyjne. Zjawisko pochłaniania światła.

Widmo emisyjne - jest to widmo wybranego typu promieniowania wysyłanego przez dany obiekt. W przypadku fal elektromagnetycznych (od mikrofal po promieniowanie rentgenowskie i gamma) emitowanych przez pojedyncze atomy (lub jądra) widmo emisyjne ma linie widmowe o ściśle określonych energiach.

Jest to rezultatem istnienia skwantowanych poziomów energetycznych - emitowane promieniowanie może mieć tylko pewne dopuszczalne energie, równe różnicy energii dwóch stanów kwantowych układu (świecenie ciał). Powstające widmo, tzw. widmo liniowe, niesie informacje o składzie chemicznym, także izotopowym (w przypadku widma emisyjnego promieniowania gamma lub alfa), źródła, co jest wykorzystywane do wykonywania analiz jego składu chemicznego i (izotopowego).

W pewnych obszarach widma emisyjnego, przy gęstej strukturze linii, obserwuje sie tzw. widma pasmowe - struktura pasm dostarcza informacji o budowie cząstek (np. widmo emisyjne podczerwone cząsteczek organicznnych). Przy zlaniu się poziomów energetycznych w szerokie pasma (jak w przypadku promieniowania cieplnego ciał stałych lub gazu w wysokiej temperaturze i pod wysokim ciśnieniem), obserwuje się widma ciągłe (np. widmo emisyjne światła żarówki lub Słońca).

Widmo absorpcyjne - jest to widmo powstające przy przenikaniu promieniowania przez materię dla niego przezroczystą. W przypadku fal elektromagnetycznych atomy ośrodka pochłaniają rezonansowo promieniowanie o energii odpowiadającej swojej strukturze energetycznej i natychmiast potem spontanicznie emitują światło, przy czym emisja owa zachodzi izotropowo.

W kierunku rozchodzenia się padającej fali elektromagnetycznej w widmie absorpcyjnym obserwuje się bardzo silne zaniki natężenia dla energii właściwych danej substancji. Umożliwia to badanie składu chemicznego absorbenta. Obrazem widma absorpcyjnego związku chemicznego są pasma o strukturze liniowej lub ciągłej z silniej lub słabiej zaznaczonymi ekstremami.

3. Zjawisko odbicia i załamania światła. Prawa Snelliusa.

Zjawisko odbicia światła - mówi, że w tej samej płaszczyźnie znajdują się: promień padający, promień odbity i normalna do powierzchni wyprowadzone w miejscu padania promienia świetlnego. Poza tym kąt padania jest zawsze równy kątowi odbicia.

Zjawisko załamania światła - mówi, że stosunek sinusa kąta padania do sinusa kąta załamania promienia świetlnego na granicy dwóch ośrodków równa się względnemu współczynnikowi załamania światła drugiego ośrodka względem pierwszego czyli stosunkowi bezwzględnego współczynnika załamania ośrodka drugiego do bezwzględnego współczynnika załamania ośrodka pierwszego.

Bezwzględny współczynnik załamania światła określany jest wzorem:

N = c/v

v - prędkość światła w danym ośrodku

c - prędkość światła w próżni (c = 299 792 458 m/s)

n - bezwzględny współczynnik załamania

Znajomość bezwzględnych współczynników załamania umożliwia szybkie obliczenie prędkości światła w danych ośrodku, wg wzoru:

V = c/n

Mając bezwzględne współczynniki załamania ośrodka z którego pada światło i ośrodka do którego załamuje się światło, można obliczyć względny współczynnik załamania.

n12=n2 /n1

n1 - bezwzględny współczynnik załamania ośrodka 1 (z którego wychodzi światło)

n2 - bezwzględny współczynnik załamania ośrodka 2(do którego przechodzi światło)

n12 - współczynnik załamania (względny) ośrodka 2 względem ośrodka 1

Względny współczynnik załamania decyduje o tym jak bardzo światło ma tendencję do skręcania swego kierunku podczas przechodzenia do innego ośrodka. Inaczej mówiąc - przy dużym względnym współczynniku załamania światło będzie się silniej załamywać.

W przypadku, gdy nie ma dokładnego stwierdzenia o jaki współczynnik chodzi, najczęściej samo wyrażenie "współczynnik załamania" należy rozumieć jako "bezwzględny współczynnik załamania".

Prawa Snelliusa - opisuje zmianę kierunku biegu promienia światła przy przejściu przez granicę między dwoma ośrodkami przeźroczystymi o różnych współczynnikach załamania. Prawo to mówi, że promienie padający i załamany oraz prostopadła padania (normalna) leżą w jednej płaszczyźnie, a kąty spełniają zależność:

gdzie:

n1 — współczynnik załamania światła ośrodka pierwszego,

n2 — współczynnik załamania światła ośrodka drugiego,

θ1 — kąt padania, kąt między promieniem padającym a normalną do powierzchni granicznej ośrodków,

θ2 — kąt załamania, kąt między promieniem załamanym a normalną.

4. Zjawisko interferencji i dyfrakcji światła. Doświadczenie Younga.

Interferencja fal - nazywamy zjawisko nakładania się fal, w których zachodzi stabilne w czasie ich wzajemne wzmocnienie w jednych punktach przestrzeni, oraz osłabienie w innych, w zależności od stosunków fazowych fal. Interferować mogą tylko fale spójne, dla których odpowiadające im drgania zachodzą wzdłuż tego samego lub podobnych kierunków.
             Jeżeli fale są niespójne to
i natężenie fali wypadkowej jest równe sumie natężeń fal składowych. Podczas nakładania się fal spójnych amplituda fali wypadkowej zmienia się od
do
w zależności od wartości trzeciego członu w równaniu (1). W najprostszym przypadku, aby zaszła interferencja muszą być spełnione następujące warunki ₁=₂ oraz ₁(t)-₂(t)=const. Podczas nakładania się światła pochodzącego z dwóch źródeł nie będących laserami lub nawet pochodzących z różnych miejsc tego samego źródła nie obserwujemy interferencji. Jest to spowodowane przez emisję światła przez wzbudzone atomy w postaci skończonych ciągów falowych, których fazy początkowe zmieniają się niezależnie. Dwie fale nazywamy falami spójnymi jeżeli różnica ich faz nie zależy od czasu. Spójne fale świetlne ze zwykłych (nielaserowych) źródeł otrzymujemy metodą dzielenia światła pochodzącego z jednego źródła na dwie lub więcej wiązek. Promieniowanie w każdej z nich pochodzi od tych samych atomów źródła i ze względu na wspólne pochodzenie, wiązki te są spójne. Do podziału światła na wiązki spójne można wykorzystać zjawiska odbicia lub załamania światła.
Okazuje się jednak, że powyższe warunki są zbyt silne i interferencję możemy obserwować nawet wtedy, gdy częstości nakładających się fal nie są dokładnie równe. Również nie musimy używać źródeł o punktowych rozmiarach. W ogólności, interferujące ze sobą fale muszą mieć spełnione tzw. warunki spójności czasowej i przestrzennej.

Dyfrakcja światła - to zjawisko fizyczne zmiany kierunku rozchodzenia się fali na krawędziach przeszkód oraz w ich pobliżu. Zjawisko zachodzi dla wszystkich wielkości przeszkód ale wyraźnie jest obserwowane dla przeszkód o rozmiarach porównywalnych z długością fali. Dyfrakcja używana jest do badania fal, oraz obiektów o niewielkich rozmiarach, w tym i kryształów, ogranicza zdolność rozdzielczą układów optycznych. Jeżeli wiązka fal przechodzi przez szczelinę lub omija obiekt, to zachodzi zjawisko ugięcia. Zgodnie z zasadą Huygensa fala rozchodzi się w ten sposób, że każdy punkt fali staje się nowym źródłem fali, tak powstałe fale rozchodzą się jako fale kuliste a fala w każdym punkcie jest sumą wszystkich fal (interferencja). Za przeszkodą pojawią się obszary wzmocnienia i osłabienia rozchodzących się fal. Zjawisko dyfrakcji występuje dla wszystkich rodzajów fal np. fal elektromagnetycznych, fal dźwiękowych oraz fal materii.

Jeden z najprostszych przykładów zjawiska dyfrakcji zachodzi, gdy równoległa wiązka światła (np z lasera) przechodzi przez wąską pojedynczą szczelinę zwaną szczeliną dyfrakcyjną. Zgodnie z zasadą Huygensa każdy punkt szczeliny o szerokości d, jest nowym źródłem fali. Między źródłami zachodzi interferencja, co powoduje wzmacnianie i osłabianie światła rozchodzącego się w różnych kierunkach. Dla pojedynczej szczeliny jasność w funkcji kąta odchylenia od osi przyjmuje postać:
, gdzie: I - intensywność światła, I₀ - intensywność światła w maksimum czyli dla kąta równego 0, λ - długość fali, d - szerokość szczeliny, funkcja sinc(x) = sin(x)/x.

Przepuszczenie fali przez szczelinę dyfrakcyjną pozwala na określenie kierunku rozchodzenia się fali. Im mniejsza jest szerokość szczeliny, tym dokładniej można to zrobić. Jednocześnie zmniejszanie szczeliny powoduje, że trudniej jest określić energię fali, ponieważ rozprasza się ona na większy obszar. W efekcie iloczyn błędu określenia energii oraz błędu pomiaru kierunku musi być większy od pewnej stałej. Oznacza to, że istnieje granica dokładności pomiaru parametrów rozchodzącej się fali. Zjawisko to ma fundamentalne znaczenie, jeżeli weźmie się uwagę, że każda materialna cząstka jest falą. Zjawisko to jest potwierdzeniem zasady nieoznaczoności. Dualizm korpuskularno-falowy powoduje, że możliwa jest obserwacja dyfrakcji cząstek materialnych. Eksperymenty udowodniły, że zjawisko to zachodzi dla elektronów i neutronów Aby wzmocnić falę przechodzącą przez szczelinę stosuje się w optyce układy wielu takich szczelin, nazywane siatką dyfrakcyjną Efekty optyczne od każdej szczeliny dodają się, przez co zachowanie fali zależy tylko od stałej siatki. Zjawisko dyfrakcji zachodzi również, kiedy fale przechodzą przez wiele blisko siebie położonych warstw. Jeżeli odległość między warstwami jest stała, kolejne maksima fali można opisać zależnością:
gdzie: d - stała siatki, θ - kąt od osi wiązki światłą, λ - długość fali, m - przyjmuje wartości od 1 do nieskończoności

Dla promieniowania rentgenowskiego zjawisko to pozwala na obserwacje kolejnych warstw kryształu. W świetle widzialnym dyfrakcję na warstwach można obserwować jako rozproszenie światła białego na powierzchni płyty CD. Kolejne ścieżki tworzą, następujące po sobie warstwy, na których fale o różnych kolorach, załamują się pod różnym kątem. W efekcie światło białe rozdziela się na poszczególne barwy. Jeżeli prześledzimy zachowanie się fali, która omija przeszkodę mniejszą niż dwie długości fali, okaże się, że fala nie reaguje na tak mały obiekt. Fakt ten powoduje konieczność stosowania krótszych fal do obserwacji mniejszych przedmiotów. Aby obserwować strukturę krystaliczną materii, konieczne jest użycie fal rentgenowskich. Zjawisko dyfrakcji pozwoliło na rozwój krystalografii rentgenowskiej, dzięki której odkryto strukturę spirali DNA. W procesie produkcji układów scalonych wykorzystuje się światło do rysowania kształtu obwodu elektrycznego na podłożu. Zjawisko dyfrakcji zmusza producenta mikroprocesorów do zastosowania fal dwa razy krótszych niż, konieczna precyzja struktury układu. Dla obwodów o dokładności 0,13 μm, oznacza to konieczność posłużenia się ultrafioletem. Jeżeli układy scalone mają się rozwijać zgodnie z prawem Moore'a, konieczne jest wdrożenie nowych technologii opierających się na falach mniejszej długości. Światło ulega największemu załamaniu w narożach i zakrętach ścieżek maski, konstruktorzy obecnie tak modyfikują maskę w narożach otworów i na zakrętach ścieżek by zminimalizować dyfrakcję, długość światła dobiera się tak by pierwsze prążki interferencyjne równoległych ścieżek nie nakładały się, poprawiono własności emulsji. Po dokonaniu tych zmian ww kryterium długości fali udało się złagodzić.

Doświadczenie Younga - eksperyment polegający na przepuszczeniu spójnego światła poprzez dwa pobliskie otwory w przesłonie i rzutowaniu na ekran. Na ekranie wskutek interferencji tworzą się charakterystyczne prążki, tzn. obszary w których światło jest wygaszone lub wzmocnione.

Warunek powstania maksimum:

Warunek powstania minimum:

gdzie:

* d - odległość między szczelinami,

* λ - długość fali

* αk - kąt pod jakim tworzy się k-te maksimum lub minimum i może być widoczne na ekranie (względem prostej przechodzącej przez środek odległości między szczelinami w kierunku padającego na nie promienia światła).

Eksperyment potwierdził falową naturę światła i stanowił poważny argument przeciwko korpuskularnej koncepcji światła, której zwolennikiem był Isaac Newton. Po raz pierwszy eksperyment ten wykonał około roku 1805 Thomas Young, fizyk angielski.

Bardziej widowiskowy i łatwiejszy sposób wykonania tego doświadczenia, polega na użyciu siatki dyfrakcyjnej, czyli płytki ze szkła, na której gęsto zarysowane są rysy pełniące rolę przesłon pomiędzy szczelinami. Obraz interferencyjny widoczny w tym przypadku na ekranie jest znacznie wyraźniejszy i jaśniejszy niż przy użyciu jedynie dwóch szczelin.

Thomasa Younga zainspirowały obserwacje fal na wodzie pochodzących z dwóch różnych źródeł - ich wzajemne wzmacnianie się i osłabianie. Chcąc wykonać podobny eksperyment z użyciem światła, użył nieprzezroczystego materiału, w którym wyciął dwie bardzo małe dziurki. Do uzyskania spójnego światła Young przepuścił światło świecy najpierw przez pojedynczy mały otwór. Światło to, zgodnie z Zasadą Huygensa rozchodziło się w postaci fali kulistej a następnie docierało do dwóch szczelin na kolejnej przesłonie. Różnica faz promieni dochodzących do obu szczelin była cały czas jednakowa dla danej częstotliwości, a zatem były to fale spójne. Po przejściu przez obie szczeliny, promienie rozprzestrzeniały się (znów zgodnie z zasadą Huygensa) i oświetlały ekran tworząc na nim kolorowe prążki interferencyjne.

Doświadczenie w swojej pierwotnej formie nie budziło wielkich kontrowersji w świecie fizyki, jednak późniejsze jego modyfikacje postawiły przed fizykami znaki zapytania. Okazało się bowiem, że nawet pojedyncze fotony wysyłane przez szczeliny w znacznych odstępach czasu, które nie miały prawa wzajemnie ze sobą interferować, tworzyły za szczelinami na światłoczułym materiale wzór interferencyjny. Efekt ten będąc jedną z manifestacji kwantowej natury światła jest często używany do objaśniania podstaw mechaniki kwantowej.

W kwantowo-mechanicznym podejściu efekt interferencji spowodowany jest nakładaniem się funkcji falowej opisującej stan fotonu.

5. Dualizm korpuskularno - falowy światła. Kwant światła, energia kwantu.

Dualizm korpuskularno - falowy - cecha wielu obiektów fizycznych (np. światła czy elektronów) polegająca na tym, że w pewnych sytuacjach, zachowują się one jakby były cząstkami (korpuskułami), a w innych sytuacjach jakby były falami.

Wg mechaniki kwantowej właściwie całą materię charakteryzuje ten dualizm. Każdej cząstce, a nawet każdemu obiektowi makroskopowemu można przypisać charakterystyczną dla niego funkcję falową, wynikającą z probabilistycznej natury materii. Z drugiej strony każde oddziaływanie falowe można opisać w kategoriach cząstek.

Energia kwantu :

E = hv

Wzór Plancka mówi, jaką energię zaabsorbowało dane ciało :

E = nhv , n  N

n - częstotliwość;

E - energia;

h - stała Plancka;

n - ilość kwantów zaabsorbowanych przez ciało.

6. Przyrządy spektralne: spektografy, spektrometry. Siatka dyfrakcyjna i jej zastosowanie.

Spektograf jest to przyrząd optyczny służący do otrzymywania widma analizowanego światła, w którym widmo to rejestruje się na błonie fotograficznej. Najczęściej stosuje się spektografy pryzmatyczne i siatkowe, w których rozszczepienie światła uzyskuje się dzięki dyfuzji światła na siatce dyfrakcyjnej. Istnieją również spektrometry masowe dynamiczne: rezonansowe i impulsowe. W spektrometrach masowych rezonansowych wiązka jonów przenika przez obszar elektrod, do których przyłożone jest pole elektromagnetyczne wysokiej częstości. Spektografy różnią się od spektometrów tym, że luneta jest zastąpiona obiektywem, w którego płaszczyźnie ogniskowej obrazowej widmo jest utrwalane na błonie fotograficznej. Spektometr masowy jest to urządzenie do rozdzielania wiązek cząstek naładowanych (zwykle jonów ), według wartości stosunku masy cząstki ładunku, za pomocą pól elektrycznych i magnetycznych. Rozdzielone wiązki są rejestrowane na błonie fotograficznej (spektograf) lub w licznikach cząsteczek. Pierwszym spektometrem masowym skonstruowanym przez Thomsona, zastosowano pole elektrostatyczne i równoległe do niego pole magnetyczne. Odchylone jony o tej samej masie, lecz różnych prędkościach układały się na paraboli. Obecnie istnieje wiele typów spektometrów masowych ( Astona, Dempstera i inne ) różniących się rodzajem i kierunkiem pól, kształtem obszaru ich działania i rozkładem ich natężeń.

Siatka dyfrakcyjna - jeden z najprostszych przyrządów do przeprowadzania analizy widmowej. Tworzy ją układ równych, równoległych i jednakowo rozmieszczonych szczelin. Jest to przezroczysta lub półprzezroczysta płytka - kryształowa, szklana lub z tworzywa sztucznego. Na jedną ze stron płytki zostaje naniesiona seria równoległych nieprzezroczystych linii, o stałym i odpowiednio małym rozstawie - od kilkunastu linii na milimetr aż do tysiąca w przypadku dobrych siatek. Działanie siatki dyfrakcyjnej polega na wykorzystaniu zjawiska dyfrakcji i interferencji światła do uzyskania jego widma. W tym celu pomiędzy źródłem światła a białym ekranem umieszcza się siatkę dyfrakcyjną. Na ekranie uzyskuje się w ten sposób widmo światła. Jako pierwszy w swoich doświadczeniach prymitywną siatkę dyfrakcyjną zastosował angielski fizyk Thomas Young. Typowa siatka dyfrakcyjna posiada 12000 szczelin na cal (tj. na 2,54 cm) szerokości. Stała takiej siatki wynosi 2116 nm (d = 2,54cm/12000). Została wynaleziona w 1821 roku przez Fraunhofera. Była pierwszym instrumentem pozwalającym wyznaczyć długość fal świetlnych. Prążki jasne powstają dla kątów α_n spełniających warunek:

dsin(α_n) = nλ gdzie:λ - długość fali, d - stała siatki, n - rząd ugięcia

2. Opracowanie części doświadczalnej

1. Analiza wykonanego ćwiczenia

Włączyłem oświetlenie pola widzenia lunety oraz skali i wyregulowałem jasność pola widzenia lunety. Umieściłem siatkę dyfrakcyjną na stoliku spektrometru prostopadle do padającej wiązki światła. Obracając całym mechanizmem znalazłem widmo I rzędu z prawej strony linii centralnej. Następnie znalazłem widmo I rzędu po lewej stronie linii centralnej. Zmierzone wartości katów zapisałem w tabeli 1. Następnie w miejsce lampy sodowej ustawiłem rurke z helem. Obracając całym mechanizmem znalazłem widmo I rzędu z prawej i z lewej strony linii centralnej dla barwy fioletowej, zielonej, żółtej i czerwonej. . Zmierzone wartości katów zapisałem w tabeli 2. Następnie obliczyłem stałą d siatki dyfrakcyjnej przyjmując długość fali  = 589,3 nm. Następnie obliczyłem długość fali dla wszystkich obserwowanych linii w widmie otrzymanym przy pomocy świecącej rurki helu ze wzoru:

n *  = dsin , n = 1

2. Wnioski

Ćwiczenie zostało wykonane zgodnie z poleceniami znajdującymi się w opisie ćwiczenia, polegało ono na wyznaczeniu długości fali świetlnej przy pomocy siatki dyfrakcyjnej. Wyniki zestawione w tabelach są przybliżone do wartości podawanych w tabelach fizycznych. Ewentualne błędy, które mogły wystąpić są spowodowane błędami w odczycie na spektrometrze.

---