Zaliczone

Pracownia Zakładu Fizyki Politechniki Lubelskiej	Kierunek studiów: Zarządzanie i Marketing
Imię i nazwisko: Łukasz Bojarski	Prowadzący laboratorium: mgr Marianna Bobyk
Wydział: ZiPT Grupa: ZiM 3.1	Data wykonania ćwiczenia: 8.10.1999

Temat: WYZNACZANIE PRĘDKOŚCI FALI GŁOSOWEJ METODĄ REZONANSU (M 5.2)

1. Cel ćwiczenia, podstawy teoretyczne.

W rurze zamkniętej jednostronnie znajduje się słup powietrza, który możemy wprowadzić w ruch drgający, który zachowuje analogię z falą stojącą. Węzeł otrzymamy przy zamkniętym końcu rury, a strzałkę przy jej końcu otwartym. Powstawanie strzałki i węzła możemy zaobserwować zbliżając kamerton do pionowo ustawionej menzurki wypełnionej cieczą. Kamerton pobudzony do drgań będzie źródłem fali biegnącej, która ulegnie odbiciu na granicy powietrze-ciecz i w wyniku interferencji z falą padającą wytwarza falę stojącą. Jeśli dobierzemy odpowiednio długość słupa cieczy, zaobserwujemy zjawisko rezonansu przejawiające się w otrzymaniu maksymalnej amplitudy drgań słupa powietrza i maksymalnego natężenia dźwięku wydobywającego się z rury (warunek rezonansu: częstotliwość drgań własnych słupa powietrza i kamertonu musi być taka sama). Drgania własne zostaną wzbudzone w słupie powietrza, jeśli jego długość będzie równa nieparzystej wielokrotności ćwiartki fali wywołanej drganiami kamertonu.

długość fali

wysokość słupa powietrza n=0,1,2,3,...

Korzystając z zależności v=f obliczamy prędkość rozchodzenia się fali głosowej w powietrzu w temperaturze otoczenia T. Prędkość fali głosowej przy temperaturze T₀=273K wyraża się wzorem:

2. Wykonanie ćwiczenia

Przygotowujemy przyrząd pomiarowy przedstawiony na poniższym rysunku:

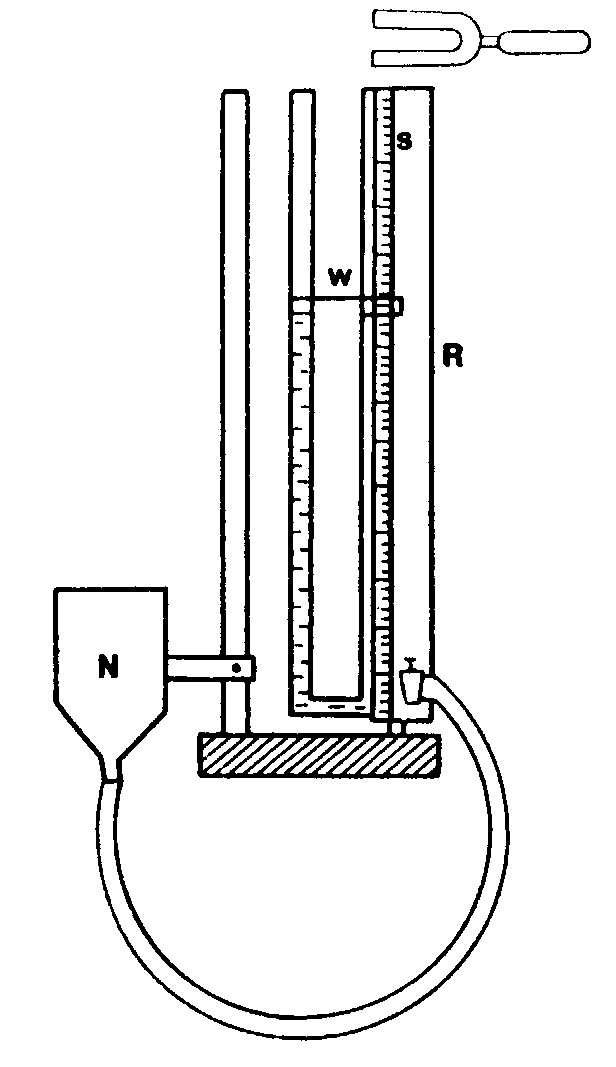
R - rura z wodą

S - skala, na której odczytujemy wysokość słupa wody

N - naczynie z wodą połączone z rurą R wężem gumowym

W - wskazówka

Między rurę R i naczynie N wstawiamy kran umożliwiający łączenie lub rozdzielanie naczyń R i N

Położenie zbiornika N zmieniamy regulując wysokość słupa powietrza w rurze R. Nad rurą R umieszczamy kamerton. Aby dokonać pomiaru długości fali  odkręcamy kran i podnosimy naczynie N jak najwyżej - jest to minimalna wysokość słupa powietrza w rurze. Zamykamy kran i opuszczamy zbiornik N na dół. Wprawiając kamerton w drgania odkręcamy częściowo kran, co spowodowało powolne obniżanie się poziomu wody w rurze. Przy wysokości słupa powietrza równej
wystąpi zjawisko rezonansu, co przejawi się maksymalnym natężeniem dźwięku. W tym momencie zamykamy kran i ustawiamy wskazówkę W na poziomie wody w rurze (pierwszy węzeł fali stojącej) i dokonujemy odczytu
. Pomiaru dokonujemy 10-krotnie. Następnie analogicznie wyznaczamy położenie
drugiego węzła fali, mając świadomość wystąpienia zjawiska rezonansu przy wysokości słupa powietrza
. Następnie obliczamy długość fali, korzystając z faktu, że
. Tak więc ostatecznie otrzymujemy
. Do pomiaru temperatury wykorzystujemy termometr.

3. Pomiary i obliczenia

Otrzymane wyniki pomiarów zamieszczamy w poniższej tabeli:

Obliczamy wartość średnią wysokości słupa powietrza. Wartość średnia wyraża się następującym wzorem:

gdzie l_i oznacza i-ty pomiar wysokości słupa powietrza, a n- liczbę pomiarów.

Obliczenia zaprezentuję kolejno dla l₁ i l₂, gdzie l₁ - wysokość słupa powietrza dla
, l₂ - wysokość słupa powietrza dla
.

Obliczamy błędy pozorne (residua) poszczególnych pomiarów, wiedząc, że:

r_i(l₁)=l₁-l₁ r_i(l₂)=l₂-l₂

Obliczenia zaprezentuję przykładowo dla pierwszych pomiarów l₁ i l₂. Wyniki kolejnych obliczeń zamieszczamy w tabeli.

r_i(l₁)=l₁₍₁₎-l₁=180 - 173=7

r_i(l₂)=l₂₍₁₎-l₂=570 - 564=6

Następnie obliczam kwadraty błędów pozornych dla poszczególnych pomiarów, wiedząc, że:

r_i²(l₁)=(l₁-l₁)²

r_i²(l₂)=(l₂-l₂)²

Obliczenia zaprezentuję przykładowo dla ostatnich pomiarów l₁₍₁₀₎ i l₂₍₁₀₎. Wyniki kolejnych obliczeń zamieszczam w tabeli.

r₁₀²(l₁₍₁₀₎)=(l₁₍₁₀₎-l₁₍₁₀₎)²=(174-173)²=1

r₁₀²(l₂₍₁₀₎)=(l₂₍₁₀₎-l₂₍₁₀₎)²=(564-564)²=0

Obliczam sumy kwadratów r_i dla l₁ i l₂:

Ponieważ nie mamy podanych wartości prawdziwych l₁ i l₂, dlatego też możemy obliczyć jedynie wartość średnią l₁ i l₂ jako przybliżenie wartości prawdziwych. Średni błąd kwadratowy pojedynczego pomiaru zapiszemy wówczas jako:

Błąd standardowy
określa błąd przypadkowy pojedynczego pomiaru, a jego wartość nie zależy od liczny pomiarów danej serii, a tylko od własności mierzonego obiektu i warunków, w jakich jest wykonywany pomiar.

Wyniki pomiaru wysokości słupa powietrza zapiszemy przy kryterium 3-sigmowym:

czyli

co oznacza, że w tych przedziałach można z prawdopodobieństwem p=99,7% oczekiwać wartości rzeczywistych l₁ i l₂.

Po analizie stwierdzam, że nie popełniliśmy błędów grubych, gdyż każde

oraz
.

Wielkością, która pozwala nam ocenić o ile wyznaczona wartość
i
różni się od wartości rzeczywistej jest „błąd standardowy średniej”, tak zwany „średni błąd kwadratowy średniej arytmetycznej” -
i
:

Następnie obliczamy prędkość fali głosowej
w temperaturze T:

Obliczamy odchylenie standardowe (średni błąd kwadratowy)
dla wielkości obliczanej (arytmetycznej)
korzystając ze wzoru:

Obliczam pochodne cząstkowe różniczkując wzór
:

Podstawiam pochodne cząstkowe do wyjściowego wzoru:

Korzystając z kryterium 3-sigmowego: 3
, określamy przedział, w którym (z prawdopodobieństwem p=99,7%) znajduje się wartość prędkości fali głosowej.

Obliczamy maksymalny błąd względny (błąd, którego faktycznie popełniony błąd nie przekracza) wielkości
różniczkując wzór

Obliczam pochodną cząstkową
:

i podstawiam pochodne do wzoru:

Temperaturę mierzymy za pomocą termometru, przyjmując, że błąd pomiaru odpowiada wartości najmniejszej działki skali stosowanego termometru:

(T = t + 273)

więc

Niedokładność pomiaru wysokości słupa powietrza wynika z niedokładności odczytu, którą przyjmujemy:

Podstawiam wartości liczbowe z pierwszego pomiaru i obliczam błąd maksymalny możliwy do popełnienia:

4. Wnioski

• Większy wpływ na niedokładność pomiaru prędkości fali głosowej w powietrzu miały odczyty wysokości słupa powietrza l₁ i l₂, co wiąże się z różną reakcją na głośność dźwięku, osób przeprowadzających pomiary.

• Aby zmniejszyć niedokładność pomiaru prędkości fali głosowej w powietrzu, należałoby zastosować metodę pozwalającą z większą dokładnością określić wartość wysokości słupa powietrza.

• Błąd pomiaru prędkości fali głosowej w powietrzu był niewielki, dlatego wyznaczanie prędkości fali głosowej w powietrzu metodą rezonansu może być z powodzeniem stosowane w warunkach laboratoryjnych

• Nie było błędu grubego, co wskazuje na poprawność przeprowadzonych pomiarów

• Zastosowanie kryterium 3-sigmowego pozwoliło nam określić przedział, w którym z dużym prawdopodobieństwem znajduje się wartość rzeczywista wyznaczanej przez nas wielkości fizycznej.

---