Kudźma Zygmunt*

OPÓŹNIENIA W HYDROSTATYCZNYCH UKŁADACH

NAPĘDOWYCH STEROWANYCH DŁAWIENIOWO

1. Wprowadzenie

W ostatnim czasie zauważa się tendencję do stosowania w napędach hydrostatycznych wyższych wartości ciśnień, jak również wzrostu prędkości przepływu cieczy roboczych przez elementy składowe tychże układów. Tendencje te wynikają z dążenia projektantów do minimalizacji wymiarów gabarytowych elementów hydraulicznych przy jednoczesnym zapewnieniu jak najwyższej wartości wskaźnika mocy generowanej lub przenoszonej do masy jednostkowej, czyli kW/kg [1]. Ten kierunek działania podyktowany jest dążeniem do uzyskania większej wydajności maszyn roboczych z napędem hydrostatycznym. Ze wzrostem prędkości przepływu w elementach hydraulicznych jednak należy się liczyć ze spadkiem sprawności hydraulicznej związanej ze stratami ciśnienia, które dla przepływu turbulentnego, rosną parabolicznie wraz z prędkością przepływu. Drugim ograniczeniem zwiększenia szybkości działania hydrostatycznego układu napędowego jest zjawisko kawitacji.

Kawitacja jest zjawiskiem polegającym na gwałtownej przemianie fazowej - z fazy ciekłej w fazę gazową pod wpływem zmiany ciśnienia. Jeżeli ciecz gwałtownie przyśpiesza, zgodnie z zasadą zachowania energii, ciśnienie statyczne płynu musi zmaleć..

W olejach stosowanych w układach hydraulicznych zawarta jest pewna ilość (10 Ⴘ 12%) rozpuszczonego powietrza. Ciśnienie parowania najbardziej lotnych frakcji takich olejów w zakresie temperatur pracy urządzeń z napędem hydrostatycznym, jest bardzo niskie, więc kawitacja w tych układach polega w pierwszej fazie na uwalnianiu i wydzielaniu się powietrza. Zjawisko to zwane jest aeracją. Ze względu na to jednak, że warunki powstawania pęcherzy par cieczy i wydzielanie się powietrza oraz częściowo skutki tych zjawisk są podobne przyjęto dla procesu wydzielania się powietrza w hydrostatycznych układach również nazwę kawitacji. Kawitacja pojawia się wtedy, gdy wartość ciśnienia w dowolnym punkcie obwodu hydraulicznego spadnie poniżej poziomu nasycenia dla danej temperatury. Na rys.1 przedstawia się, za pracą [11] graficznie zależność wartości ciśnienia p_kaw, przy której następuje wydzielanie się powietrza w postaci pęcherzyków z oleju hydraulicznego w funkcji temperatury.

Po aproksymacji punktów pomiarowych otrzymano zależność:

P_kaw = (4,36t + 39,13)·10² (1)

gdzie: t [^oC], p_kaw [N/m²].

Jak wynika z przedstawionych ograniczeń zwiększenia wydajności maszyn roboczych z napędem hydrostatycznym można poszukiwać w odpowiednio zaprogramowanych właściwościach dynamicznych tych układów. Wiąże się to z dopuszczalnym, ze względu na obciążenia dynamiczne, skróceniem czasów rozruchu i hamowania..

* dr inż. Kudźma Zygmunt Instytut Konstrukcji i Eksploatacji Maszyn Pol. Wrocławska.

Rys. 1. Wpływ temperatury na wartość ciśnienia(ciśnienie bezwzględne) wydzielania się powietrza z oleju hydraulicznego HL68

W ostatnich latach zauważyć można intensywny rozwój różnego typu systemów sterowania wpływających na parametry stanów nieustalonych hydrostatycznych układów napędowych, szczególnie należy tu wymienić układy „load sensing” lub sterowane mikroprocesorowo w technice proporcjonalnej.

Należy jednak nadmienić, że ze względu na stosunkowo niski koszt jak i specyficzne warunki pracy, wiele maszyn roboczych ciężkich z napędem hydrostatycznym wyposażonych w pompy stałego wydatku sterowanych jest dławieniowo za pomocą rozdzielaczy konwencjonalnych. Projektant układu napędowego, obok tak podstawowych parametrów jak moc wyjściowa, sprawność itd., stoi przed problemem zapewnienia określonych właściwości dynamicznych ze względu na specyfikę projektowanej maszyny. W artykule przedstawiono wpływ parametrów konstrukcyjnych układu hydrostatycznego na właściwości dynamiczne.

2. Model dynamiczny układu hydrostatycznego sterowanego dławieniowo

Literatura poświęcona stanom nieustalonym w hydrostatycznych układach napędowych jest stosunkowo bogata [2, 3, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 16, 17, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29], z krajowej, kompleksowe podejście do zagadnienia prezentują książki prof. J.Tomczyka [2], oraz prof. Palczaka [3] i prof. Garbacika [7] w których, stosując różne podejście, przedstawiono podstawy tworzenia modeli dynamicznych elementów i układów. Uwzględniając współczesne techniki obliczeniowe nie jest więc problemem stworzenie i rozwiązanie modelu matematycznego stanów nieustalonych układów hydrostatycznych nawet rozbudowanych pod względem strukturalnym. Problem istotny tkwi w wiarygodności i przedziale zmienności przyjętych poszczególnych współczynników równań modelu matematycznego. Należy uwzględnić, że układy hydrostatyczne tworzą obiekty o złożonej strukturze fizycznej w których podstawowe wielkości charakteryzujące układ przyjmują zmienne wartości, np. lepkość czynnika roboczego zmieniająca się z temperaturą i w mniejszym stopniu z ciśnieniem. Pod wpływem drgań zmienia się przepływ przez szczeliny oraz siły tarcia, a więc straty wolumetryczne i opory ruchu. Z tego powodu, między innymi, te wielkości w rozważaniach analitycznych uwzględnia się poprzez pewnego rodzaju uśrednienie a odnoszące się do stanów ustalonych. O trafności przyjętych założeń upraszczających, a w efekcie o poprawności rozwiązań analitycznych decydować powinno zawsze porównanie wyników uzyskanych na drodze obliczeń i wyznaczonych doświadczalnie z określonym przedziałem ufności.

Model dynamiczny układu hydraulicznego z silnikiem tłokowym i pompą stałej wydajności przedstawiono w sposób poglądowy na rys 2.

Rys.2. Model układu hydraulicznego z silnikiem tłokowym i pompą stałej wydajności:
Qpt, - wydajność teoretyczna pompy, Qs - chłonność silnika (cylindra hydraulicznego),
Qv - straty przecieków, Qc - przepływ wywołany ściśliwością cieczy oraz

od­kształceniami elementów układu hydraulicznego, A - pole po­wierzchni czynnej
tłoka, v - prędkość tłoka, f - współczynnik tarcia wiskotycznego

Ze względu na strukturę analizowanego układu i charakter występujących w nim zjawisk do analizy teoretycznej wykorzystano model układu o parametrach skupionych, opisany równaniami różniczkowymi zwyczajnymi i algebraicznymi przyjmując powszechnie stosowane założenia upraszczające [2, 4, 5, 6, 9]. Przy przyjętych założeniach upraszczających model matematyczny rozruchu układu hydrostatycznego napędowego tworzy się według równania ciągłości przepływu ( zasada zachowania masy) oraz warunku równowagi sił działających na tłok cylindra. Równanie ciągłości przepływu w króćcu tłocznym pompy ma postać.:

Q_pt = Q_s + Q_v + Qc . (2)

Dla silnika tłokowego chłonność wyraża się związkiem

Q_s = A·v . (3)

Straty przecieków zależą liniowo od ciśnienia w układzie można więc napisać:

Q_v = a·p . (4)

gdzie: a - współczynnik proporcjonalności, którego wartość można określić na podstawie

charakterystyk statycznych elementów z których zestawiony został układ, p - wartość

ciśnienia w układzie.

Przepływ wywołany ściśliwością i odkształceniami elementów określany jest wg relacji:

Qc = Kc·
, (5)

gdzie: Kc - pojemność ściśliwości układu (kapacytancja)

Równanie ciągłości przepływu w postaci:

Qpt = A·v + a·p + Kc·
_, (6)

oraz równanie równowagi sił działających na tłok cylindra w postaci:

m_zr·
+ f·v + F = p·A , (7)

gdzie: m_zr - zredukowana masa obciążenia zewnętrznego i cieczy roboczej, f - współczynnik
tarcia płynnego określany na podstawie sprawności mechanicznej cylindra i sprawności

hydraulicznej obwodu, F - obciążenie zewnętrzne, A - pole powierzchni czynnej tłoka,

t - czas.

pozwalają po rozwiązaniu, na określenie przebiegu ciśnienia podczas rozruchu analizowanego układu.

Dla rozpatrywanego układu (rys.2) rozruch układu odbywa się w dwóch etapach:

Etap l - obejmuje okres od momentu przesterowania rozdzielacza do chwili, w której w

układzie wystąpi ciśnienie p_u o wartości odpowiadającej obciążeniu zewnętrznemu,
tłok cylindra wraz z obciążeniem znajduje się w tym okresie w spoczynku. v = 0.

Etap 2 - w którym wszystkie masy układu są w ruchu.

Analiza 1-szego etapu rozruchu. Warunki początkowe etapu 1: v = 0, t = 0, p = 0.

Zależność ciśnienia p od czasu t w 1 etapie otrzymuje się całkując równanie bilansu przepływu (6) zestawionego dla przewodu tłocznego pompy ( pomijając człon A·v)

Rozwiązanie równania (6) jest następujące:

(8)

W chwili dla której ciśnienie osiągnie wartość p = p_u (wartość ciśnienia w ruchu ustalonym) następuje zakończenie 1 etapu rozruchu (w układzie mechanicznym odpowiada to procesowi kasowania luzów).

Czas trwania etapu 1 (czas reakcji) uzyskujemy przekształcając równanie (8):

. (9)

Warunki końcowe etapu 1,(indeks 1k) stanowiące jednocześnie warunki początkowe (indeks 2p) dla etapu 2, otrzymamy dla p = p_u uwzględniając zależność (9) w równaniu (6). Warunki te są następujące: p_1k = p_2p = p_u

_. (10)

Po przekształceniach Laplace'a i rozwiązaniu układu równań (6) i (7), w jednostkach bezwzględnych, przebieg ciśnienia w 2 etapie rozruchu hydrostatycznego układu napędowego z silnikiem tłokowym przedstawia wyrażenie:

p = p_u +
, (11)

Poszczególne symbole w wyrażeniu (11) oznaczają:

- częstość kołowa drgań własnych nie tłumionych, (12)

- częstość kołowa drgań tłumionych układu, (13)

- zredukowany (bezwymiarowy)współczynnik tłumienia. (14)

2. Wielkości kryterialne opisujące parametry rozruchu układu hydrostatycznego

Powszechnie przyjętymi wielkościami kryterialnymi, opisującymi właściwości dynamiczne układu są:

• częstość drgań własnych nietłumionych ω₀ i tłumionych ω.

• zredukowany współczynnik tłumienia ξ

• czas reakcji τ.

• czas trwania procesu przejściowego tp.

• współczynnik nadwyżki dynamicznej ciśnienia φ_d definiowany jako stosunek różnicy wartości ciśnienia maksymalnego p_max i ciśnienia w stanie ustalonym p_u do wartości ciśnienia w stanie ustalonym, czyli:

(15)

Przebieg ciśnienia p(t) po skokowym wymuszeniu natężenia przepływu Q (przy przyjęciu parametrów skupionych i założeń upraszczających [2, 4, 5]) opisany jest równaniem różniczkowym liniowym drugiego rzędu [2, 4] analogicznym jak dla jedno masowego ruchu drgającego. Poglądowo przebieg podstawowych parametrów podczas rozruchu dla dwóch wartości współczynnika tłumienia: ξ <1 i ξ >1 i z zaznaczonymi wielkościami kryterialnymi pokazano na rys. 3.

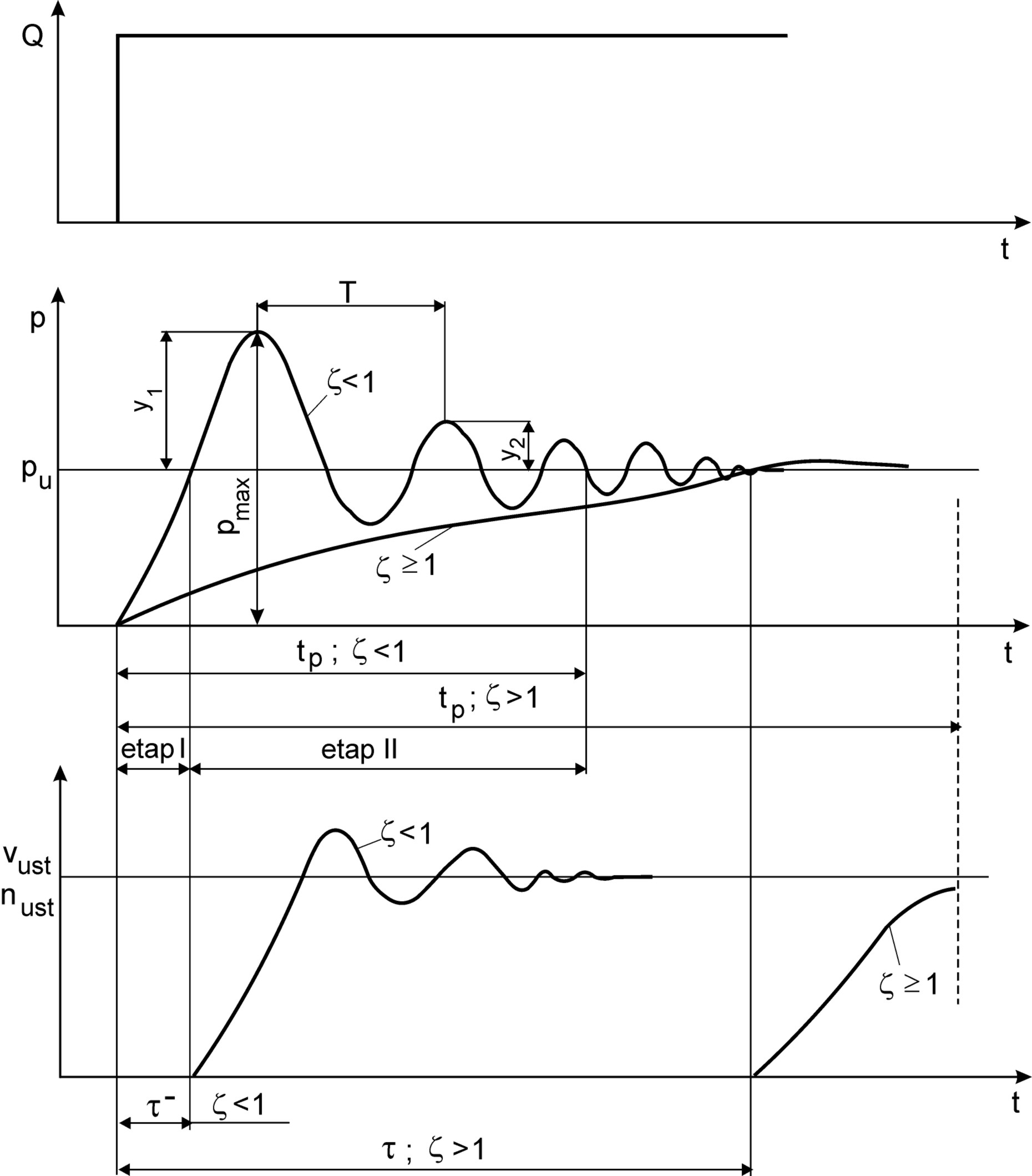
Rys. 3. Przebieg ciśnienia p, prędkości liniowej v (obrotowej n) przy skokowym
wymuszeniu natężenia przepływu Q podczas rozruchu.T - okres drgań własnych,
 - czas reakcji (zawarty pomiędzy wprowadzeniem wymuszenia a odpowiedzią
układu - początek ruchu elementu wykonawczego),  - zredukowany współczynnik
tłumienia, t_p- czas trwania procesu przejściowego

Z punktu widzenia wydajności maszyny roboczej z napędem hydrostatycznym o stanie przejściowym decydują dwa podstawowe parametry: zredukowany współczynnik tłumienia ξ

Oraz czas reakcji τ.

Tłumienie w hydrostatycznych układach napędowych

Tłumienie w hydrostatycznych układach napędowych spowodowane jest głównie występowaniem przecieków wewnętrznych, oporów związanych z przepływem cieczy roboczej oraz sił tarcia wywołanych ruchem elementu wykonawczego i mechanizmu napędzanego. Istotny wpływ na tłumienie a więc i na charakter rozruchu ma pojemność ściśliwości zależna między innymi od konstrukcji, ilości i jakości przewodów, scharakteryzowana kapacytacją układu.

Kapacytancja Kc wartość, która zależy od objętości początkowej Vo cieczy w układzie i zastępczego modułu sprężystości objętościowej Bz oleju i podatnych elementów.

Zredukowany współczynnik tłumienia ξ, po sprowadzeniu równania opisującego przebieg ciśnienia w drugim etapie rozruchu (gdy ciśnienie osiągnie wartość p_u) do postaci kanonicznej określa wyrażenie (14) (w przypadku napędu liniowego). Mając do czynienia z napędem obrotowym m_zr zastępujemy Jzr [kgm²] (zredukowany masowy moment bezwładności) a A zastępujemy q_s [m³] (chłonność właściwa silnika). O ile takie parametry jak powierzchnia czynna tłoka A, masa zredukowana m_zr lub zredukowany masowy moment bezwładności Jzr, chłonność właściwa q_s silnika nie wymagają bliższej definicji i są określone wprost na podstawie założeń projektowych układu napędowego, to pewnego wyjaśnienia wymagają pojęcia: kapacytancja układu hydrostatycznego określona współczynnikiem Kc, współczynnik przecieków wewnętrznych a, współczynnik tarcia f.

Kapacytancja

Pod pojęciem kapacytancji układu hydrostatycznego rozumiana jest podatność tego układu na odkształcenia pod wpływem ciśnienia. Zredukowana kapacytancja K_c układu jest sumą kapacytancji cieczy roboczej K_ol i elementów układu K_el, czyli:

. (16)

Ze względu na wartość ciśnień maksymalnych występujące w układach napędowych jako elementy podatne można uwzględnić tylko przewody elastyczne, natomiast przewody stalowe traktować jako nieodkształcalne.

Kapacytancję cieczy roboczej wyznacza się z zależności:

, (17)

gdzie: V_ol - objętość początkowa cieczy w sztywnych elementach, B_ol - moduł sprężystości
objętościowej cieczy roboczej.

Kapacytancję przewodów elastycznych, definiowana analogicznie jak dla cieczy, wyznacza się z zależności:

, (18)

gdzie: V_p - początkowa objętość cieczy w przewodach elastycznych, B_p - zastępczy moduł

sprężystości objętościowej przewodów elastycznych i zawartego w nich oleju.

Przewody elastyczne w porównaniu z przewodami sztywnymi odznaczają się dużą odkształcalnością sprężystą. Wyraża się to dużą zmianą ich objętości ze wzrostem ciśnienia, zwaną potocznie puchliwością. Zależy ona od konstrukcji węża, własności materiałów użytych do jego produkcji oraz technologii wykonania. Z pewnym przybliżeniem można przyjąć, że przy wzroście ciśnienia o 20 MPa następuje wzrost objętości początkowej o około 2 ÷ 2,5 %, a więc moduł B_p przyjmuje wartość na poziomie B_p = (0,7 ÷ 1)10³ MPa.

Natomiast B_ol wg [12] przyjmuje wartość B_ol = (1,25 ÷ 2,0)10³ MPa. Należy jednak zaznaczyć, że podana wartość B_ol jest wartością uśrednioną. W obliczeniach dokładnych należy jednak uwzględniać wpływ takich wielkości jak: ciśnienie, stopień zapowietrzenia czynnika roboczego, temperatury, na wartość modułu sprężystości objętościowej [12,13].

W celu zwiększenia zredukowanego współczynnika tłumienia  efektywnym sposobem jest zainstalowanie hydroakumulatora o określonej kapacytancji K_a, którą można obliczyć na podstawie zależności [14]:

, (19)

gdzie: p_o, V_o - ciśnienie i objętość gazu początkowe, V - zmiana objętości gazu,
V₁ - objętość końcowa gazu, n - wykładnik politropy.

Gdy V << V_o wzór (19) upraszcza się do postaci [14, 15]:

(20)

Ponieważ dane dotyczące modułu sprężystości przewodów elastycznych nie są, przez producentów, publikowane najwłaściwszą metodą określającą wartość tego parametru jest metoda doświadczalna opisana w dalszej kolejności.

Współczynnik tarcia f.

Współczynnik tarcia lepkiego f jest sumą odpowiednio zredukowanych współczynników tarcia lepkiego w przewodach i w cylindrze hydraulicznym: [4,16]:

, (21)

gdzie: f_p, f_s - odpowiednio zredukowane współczynniki tarcia lepkiego w przewodach i w
cylindrze.

Wartość zredukowanego współczynnika tarcia lepkiego w przewodach wg [16] określa zależność:

, (22)

gdzie: p - spadek ciśnienia w instalacji, A - powierzchnia czynna cylindra, v_ust - prędkość
ustalona tłoka.

Współczynnik f_s wyznaczyć można wg [17] z zależności przybliżonej:

, (23)

gdzie: F - obciążenie cylindra, _c - sprawność mechaniczna cylindra.

Współczynnik przecieków a

Wartość współczynnika przecieków wewnętrznych a układu hydraulicznego określa się jako współczynnik kierunkowy prostej aproksymującej efektywnego natężenia przepływu Q od ciśnienia p. Charakterystyka ta stanowi równocześnie podstawę do wyznaczania sprawności wolumetrycznej
układu

(24)

Przekształcając równanie (24) uzyskano zależność na współczynnik a przecieków wewnętrznych układu w funkcji sprawności wolumetrycznej i parametrów pracy.

(25)

3. Weryfikacja doświadczalna

Weryfikację rozwiązań teoretycznych przeprowadzono na stanowiskach badawczych realizujących ruch obrotowy i postępowy. W rozwiązaniach analitycznych wykorzystywano współczynniki równań określone empirycznie. Badania z silnikiem tłokowym przeprowadzono na stanowisku którego schemat hydrauliczny obrazuje rys. 4.

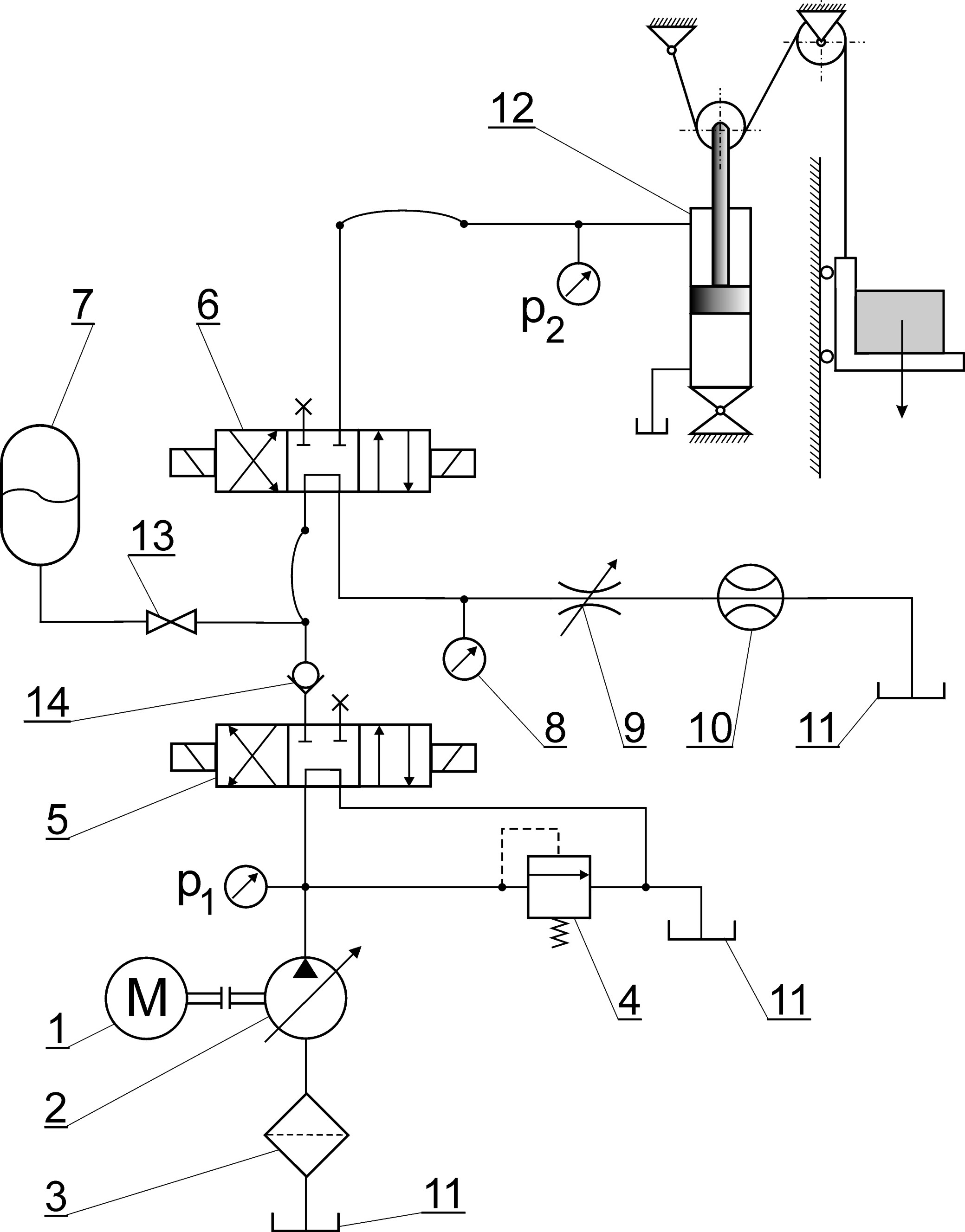
Rys. 4. Schemat hydrauliczny układu doświadczalnego z silnikiem tłokowym:
1 - silnik elektryczny, 2 - pompa wielotłoczkowa, 3 - filtr ssawny, 4 - zawór

bezpieczeństwa, 5,6 - rozdzielacz sterowany elektromagnetycznie,
7 - akumulator hydropneumatyczny, 8 - manometr, 9 - zawór dławiący,
10 - przepływomierz, 11 - zbiornik, 12 - cylinder hydrauliczny, 13 - zawór
odcinający, 14 - zawór zwrotny

Pompa wielotłoczkowa 2 typu PTOZ-40R napędzana silnikiem elektrycznym 1 typu SZD-114 (moc N = 11 kW, obroty 1400 obr/min) zasysa olej ze zbiornika 11, przez filtr ssawny 3 i podaje go przez rozdzielacze 5 i 6 typu RSR-12 z wmontowanymi przystawkami elektromagnetycznymi do cylindra hydraulicznego 12 (D = 50 mm, d = 25 mm). Cylinder obciążony był przez układ linowy i bloczki masą m_zr. Układ przed przeciążeniem zabezpieczony był zaworem maksymalnym 4 typu ZP-42. Ponadto układ badawczy wyposażony był w akumulator hydropneumatyczny 7 (p_o = 2,0 MPa, V_o =2, 5 dm³), który można było odłączyć od instalacji za pomocą zaworu odcinającego 13.Rejestrację zmian ciśnienia w układzie podczas rozruchu poprzedzono badaniami statycznymi w celu określenia wartości współczynników równań modelu matematycznego. Podstawowym celem badań było określenie wpływu kapacytancji układu na charakter rozruchu, a dokładniej na wartość współczynnika tłumienia i czas reakcji.

Kapacytancję akumulatora hydropneumatycznego korzystając z zależności definicyjnej
można określić doświadczalnie na stanowisku, którego schemat obrazuje rys. 5 poprzez zmiany objętości gazu V_g spowodowane przyrostem ciśnienia Δp. W celu uzyskania wymaganej wartości ciśnienia wykorzystano pompę 1 z napędem ręcznym (prasa do wzorcowania manometrów), natomiast zmianę objętości V_g określono za pomocą wyskalowanego naczynia pomiarowego po odpowiednim ustawieniu zaworów odcinających.

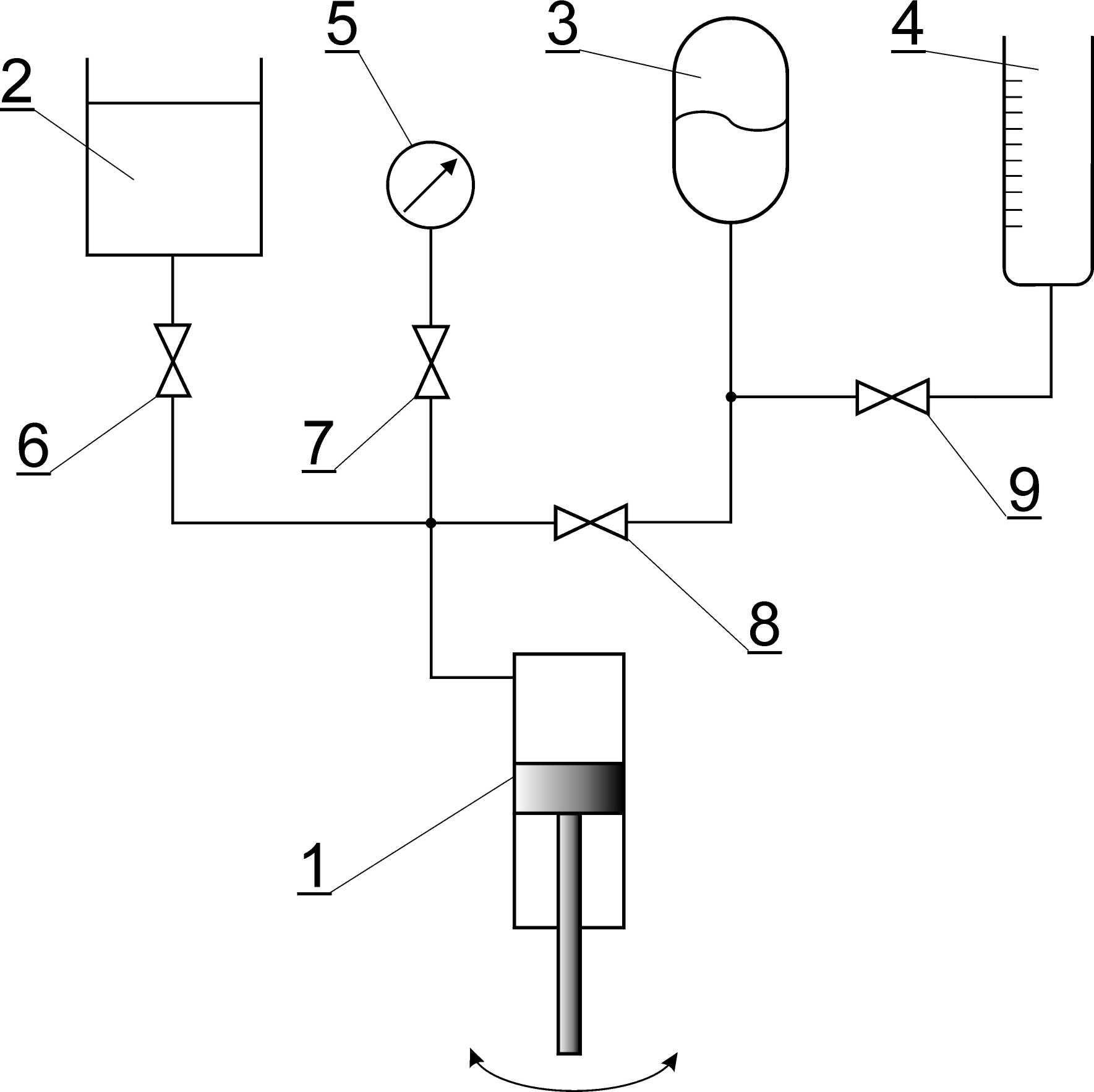
Rys. 5. Schemat układu do określania kapacytancji akumulatora hydropneumatycznego w

warunkach stacjonarnych: 1 - pompa z napędem ręcznym, 2 - zbiornik zalewowy,
3 - badany hydroakumulator, 4 - zbiornik pomiarowy, 6,7,8,9 - zawory odcinające,

warunki początkowe pracy akumulatora: V₀ = 2,5 dm³ , p₀ = 2 MPa.

Rys. 6. Zmiana objętości V_g w funkcji przyrostu ciśnienia p akumulatora hydraulicznego

Kapacytancję akumulatora hydropneumatycznego wyznaczono na podstawie pomiarów statycznych, które przedstawiono na rys. 6 przeprowadzając linaeryzację zależności V_g = f(p) w zakresie ciśnień pracy za pomocą siecznej.

Na podstawie przeprowadzonych pomiarów statycznych i geometrii układu parametry charakterystyczne wynoszą:

- powierzchnia czynna tłoka A = 14,7·10^-4 m²;

- współczynnik przecieków a = 4,6·10^-12 m⁵/Ns;

- kapacytancja układu:

bez akumulatora K_c = 4,33·10^-12 m⁵/N;

z akumulatorem K_ca = 2,1·10^-10m⁵/N;

- wydajność teoretyczna pompy Q_pt =0,63·10^-3 m³/s;

- masa zredukowana m_zr = 1220 kg;

- wartość ciśnienia w ruchu ustalonym p_u = 5 MPa;

- prędkość w ruchu ustalonym v_u = 0,41 m/s;

- spadek ciśnienia w instalacji p = 8·10⁵ N/m².

Przykładowy wynik pomiarów przebiegu ciśnienia przy skokowym wymuszeniu natężenia przepływu pokazano na rys. 7.

Rys. 7. Porównanie przebiegu ciśnienia obliczeniowego (linia kreskowa) z przebiegiem

rzeczywistym. Q_pt = 0,63·10^-3 m³/s, m_zr = 1220 kg, układ bez akumulatora

czas reakcji τ.=0,11 s.

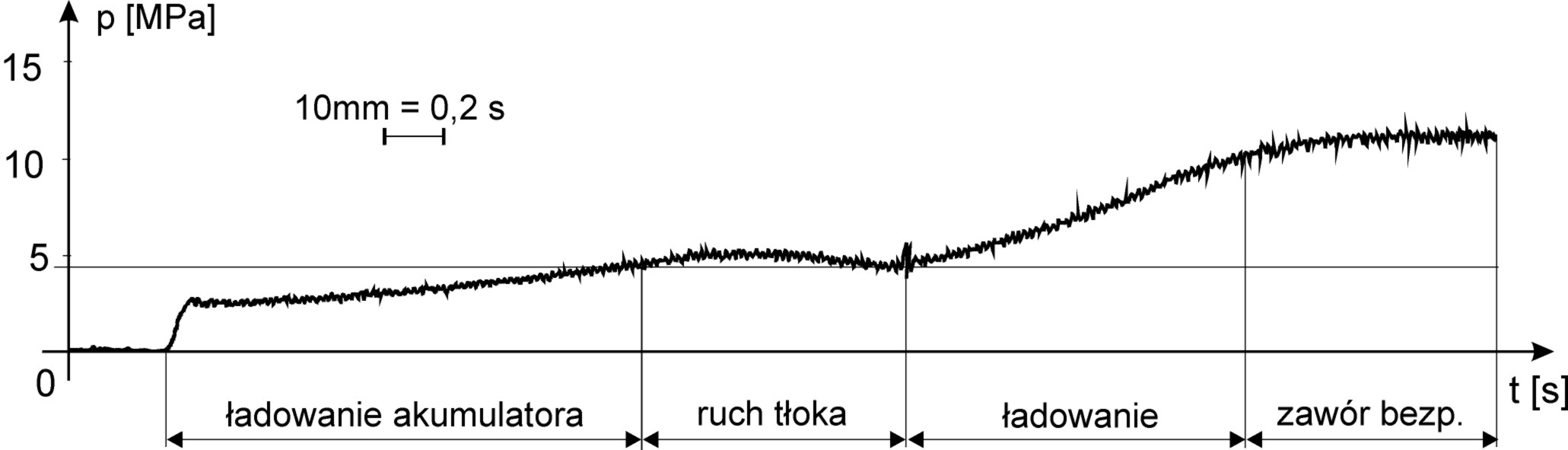
Rys. 8. Przebieg ciśnienia w punkcie p₂ (rys. 4): Q_pt = 0,63·10^-3 m³/s, m_zr = 1220 kg z udziałem akumulatora hydropneumatycznego p_o=2MPa, V ₀=2,5 dm³

Czas reakcji τ.=1,6 s.

---