Fizyka

Program przedmiotu:

15 godzin wykładu - dr Krystyna Chłędowska
20 godzin ćwiczeń audytoryjnych

www.prz.edu.pl

Wydział Matematyki i Fizyki Stosowanej
Katedra Fizyki
pracownicy

Treści kształcenia:

Dynamika układów punktów materialnych.
Elementy mechaniki relatywistycznej.
Podstawowe prawa elektrodynamiki i
magnetyzmu.
Zasady optyki geometrycznej i falowej.
Elementy optyki relatywistycznej.
Podstawy akustyki.
Mechanika kwantowa i budowa materii.
Fizyka laserów.
Podstawy krystalografii.
Metale i półprzewodniki.

Literatura
1. K. Chłędowska, R. Sikora, Wybrane problemy fizyki z

rozwiązaniami cz. I, Oficyna Wydawnicza Politechniki
Rzeszowskiej, Rzeszów 2008

2. R. Sikora, K. Chłędowska, Problemy fizyki z rozwiązaniami cz.

II, Oficyna Wydawnicza Politechniki Rzeszowskiej, Rzeszów
2002

3. D. Halliday, R. Resnick, J. Walker, Podstawy fizyki , PWN,

Warszawa 1999

4. J. Massalski, M. Massalska, Fizyka dla inżynierów, WNT

Warszawa 2005

5. C. Bobrowski, Fizyka – krótki kurs, WNT Warszawa 2003
6. J. Orear, Fizyka, WNT Warszawa 1999
7. I.W. Sawieliew, Wykłady z fizyki, PWN Warszawa 1994

Zaliczenie przedmiotu:

Uzyskanie zaliczenia z ćwiczeń
audytoryjnych

Egzamin:

Forma pisemna obejmująca:

• pytania problemowe

• szczegółowe opracowanie jednego tematu

• zadania

Dynamika układów punktów

materialnych

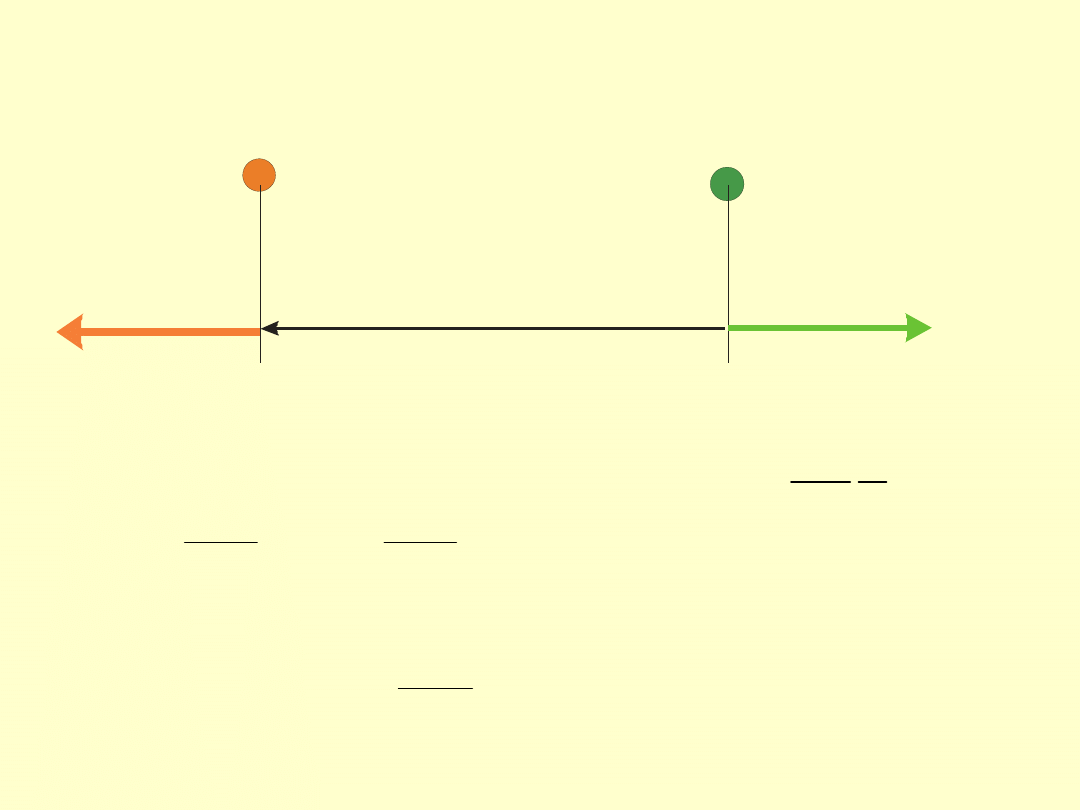
Punkt materialny – ciało obdarzone masą, ale nie

posiadające objętości. Ruch postępowy każdego

rzeczywistego obiektu można opisać jako ruch punktu

materialnego.

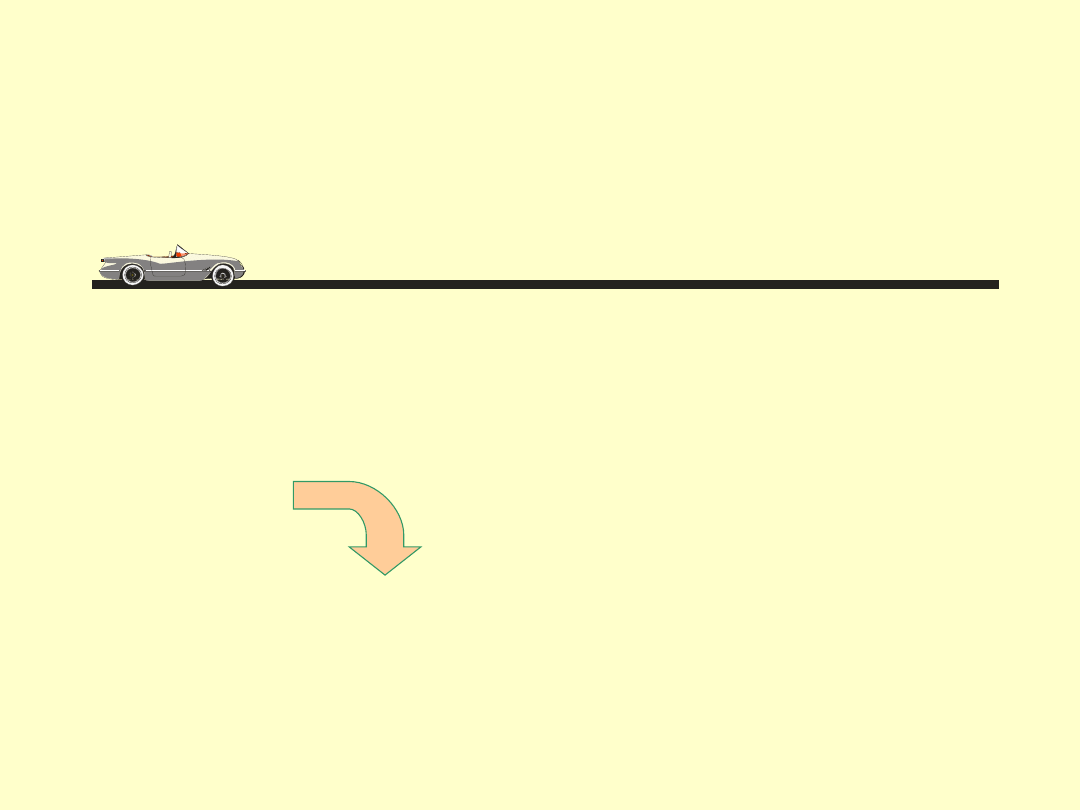
Przemieszczenia liniowe wszystkich elementów samochodu
są

jednakowe

samochód podczas ruchu prostoliniowego możemy
potraktować jak punkt materialny

Przemieszczenie liniowe elementów pręta

zależy

od

odległości od osi obrotu

A

B

Ciała obracające się nie mogą być traktowane jak punkty materialne

1. Dane jest ciało o ściśle określonych własnościach

2. Ciało umieszczamy w znanym otoczeniu –
potrafimy określić siły, które na niego działają

Pytamy:

jaki będzie ruch tego ciała?

Problem dynamiki możemy sformułować następująco:

r

F

M

m

r

r

r

Mm

G

F





2





2

2

11

10

66

.

6

kg

Nm

G







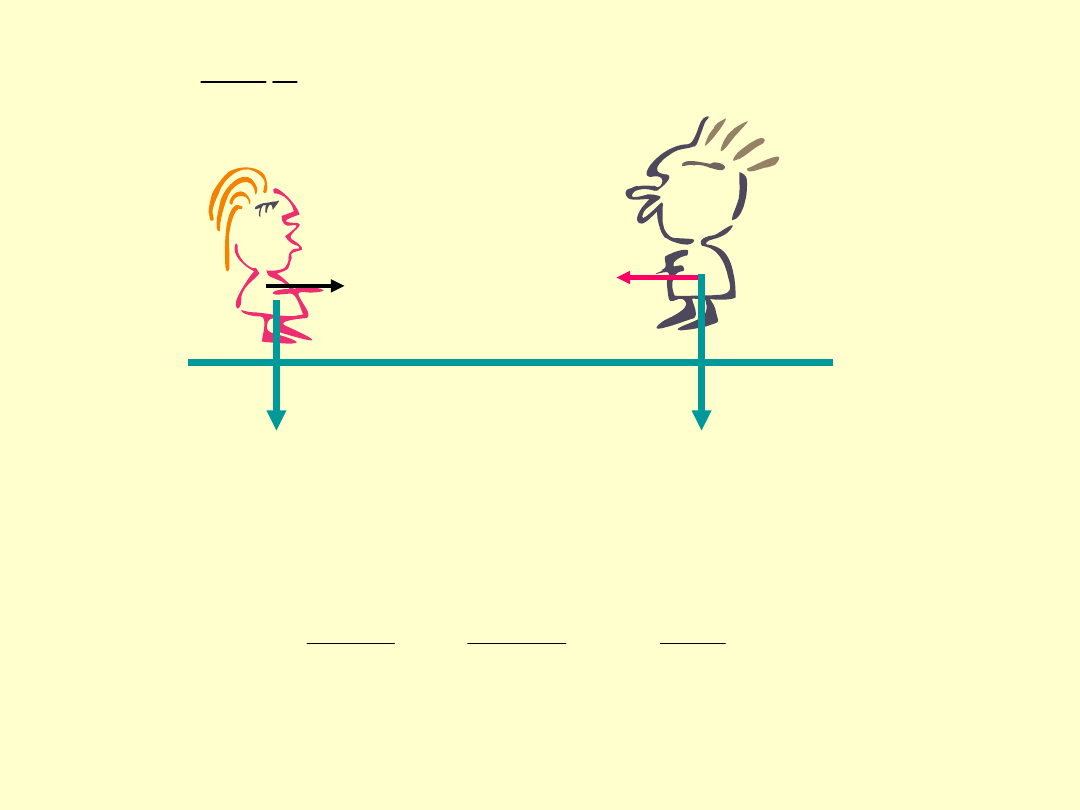
r

r

r

Mm

G

F





2





?

Ziemia

M

Z

>> M, m

2

2

2

r

Mm

G

R

M

M

G

R

m

M

G

Z

Z

Z

Z





r

+q

+Q

r

r

r

Qq

k

F





2



F

2

2

12

10

8542

,

8

Nm

C

o









2

2

9

10

9

4

1

C

Nm

k

o









k

m

kx

F 



1

F

1

Jeżeli dodatkowo występuje tarcie pomiędzy masą m a powierzchnią, to

fmg

F 

2

f – współczynnik tarcia

I

1

I

2

F

F

l

a

I

I

F

2

1

0

2

4







Am

Wb

7

0

10

4











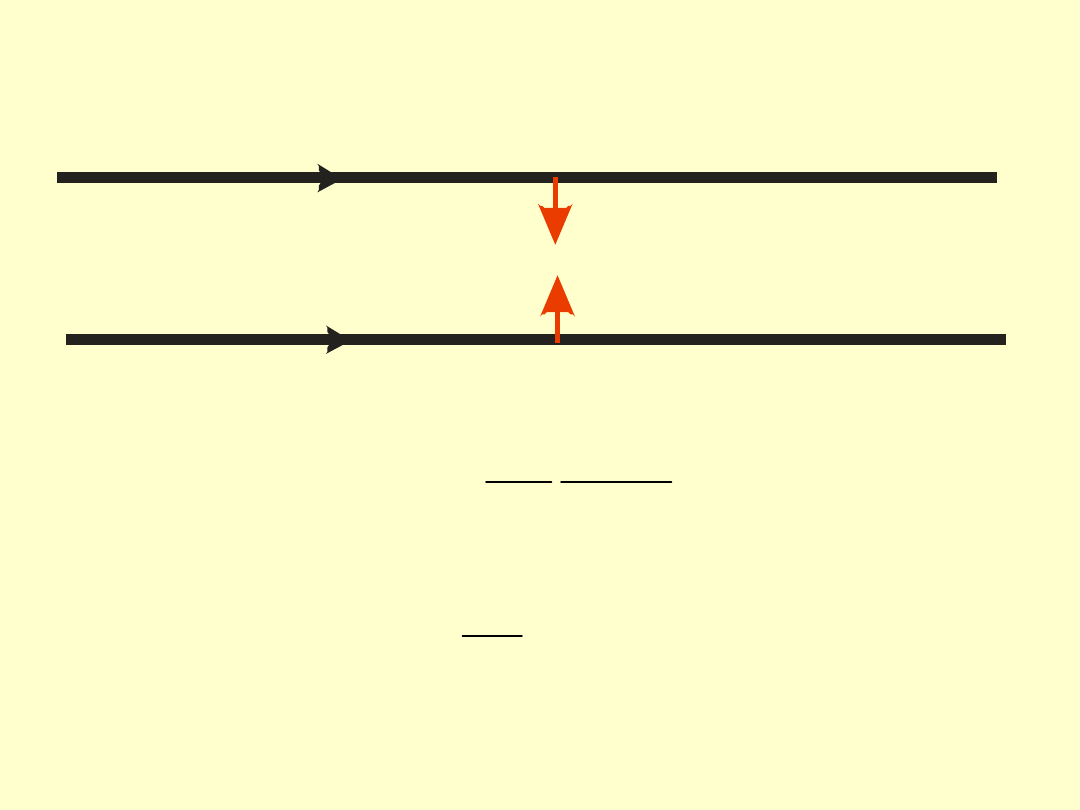
Zasady dynamiki Newtona

I zasada dynamiki

Każde ciało pozostaje w stanie spoczynku lub ruchu
jednostajnego po linii prostej dopóty, dopóki nie zostanie
zmuszone za pomocą wywierania odpowiednich sił do zmiany
tego stanu.

I zasada dynamiki stwierdza, że jeżeli w pobliżu danego ciała
nie ma innych ciał (a więc nie działają siły), to można znaleźć

taki układ odniesienia, w którym ciało nie będzie mieć
przyspieszenia.

Isaac Newton 1642-1721

Układ S spoczywa, układ S’ porusza się ze stałą prędkością v.

S’

S

Obserwator znajdujący się w układzie S’ stwierdza:

chłopiec spoczywa

Obserwator znajdujący się w układzie S stwierdza:

chłopiec porusza się z prędkością v = const.

Obydwaj obserwatorzy stwierdzą”

przyspieszenie chłopca a = 0.

Fakt, ze ciało pozostaje w spoczynku lub porusza się ze stałą
prędkością, jeśli nie przykładamy do niego żadnej siły wiąże
się z właściwością materii zwaną bezwładnością (inercją).
Układy, w których obowiązuje I zasada dynamiki nazywamy

układami inercjalnymi.

II zasada dynamiki

Jeżeli na ciało działa wypadkowa siła to przyspieszenie
tego

jest wprost proporcjonalne do działającej siły a odwrotnie do
masy ciała.

Jeśli określimy siły działające na ciało, to znając warunki
początkowe

możemy wyznaczyć położenie ciała, jego prędkość i
przyspieszenie w dowolnej chwili.

F



m

F

a







o

o

r

r

v

v

t















,

,

0

Przyspieszenie średnie

t

v

a

śr











Prędkość średnia

t

r

v

śr











W równaniu Newtona występuje przyspieszenie chwilowe

dt

v

d

t

v

a

t

chw



















0

lim

dt

r

d

t

r

v

t

chw



















0

lim

Równanie

jest równaniem wektorowym.

2

2

dt

r

d

m

dt

v

d

m

a

m

F

m

F

a



























z

y

x

F

F

F

F

F

,

,







2

2

2

2

2

2

dt

z

d

m

dt

dz

dt

d

m

dt

dv

m

F

dt

y

d

m

dt

dy

dt

d

m

dt

dv

m

F

dt

x

d

m

dt

dx

dt

d

m

dt

dv

m

F

z

z

y

y

x

x



















?

Elementy analizy matematycznej

Funkcje

Zmienna

y

nazywa się

zmienną zależną

albo

funkcją

zmiennej x

jeśli przyjmuje określone wartości dla każdej wartości zmiennej x w
jej pewnym przedziale zmienności.

)

(

)

(

x

y

y

x

f

y





lub

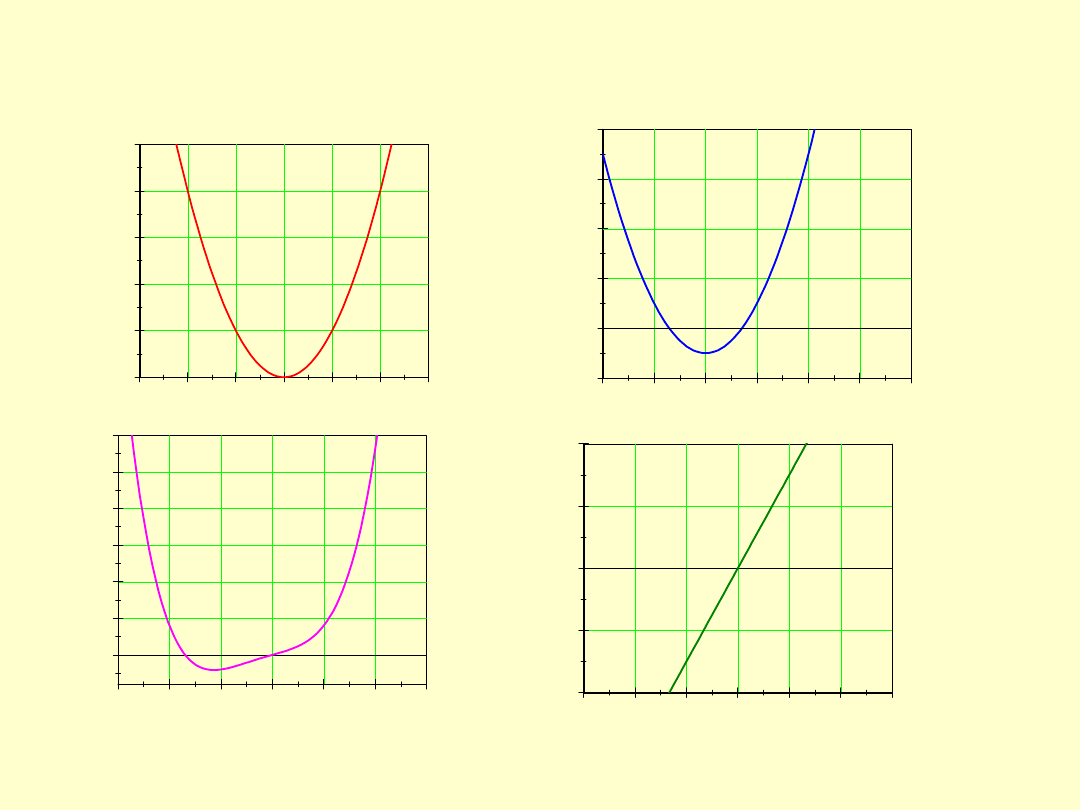
-3

-2

-1

0

1

2

3

0

2

4

6

8

10

y

x

-3

-2

-1

0

1

2

3

0

2

4

6

8

10

y

x

2

2x

y 

3

4

2

2







x

x

y

-3

-2

-1

0

1

2

3

0

5

10

15

20

25

30

y

x

x

x

x

y

2

3

4







-3

-2

-1

0

1

2

3

-4

-2

0

2

4

y

x

x

y 3



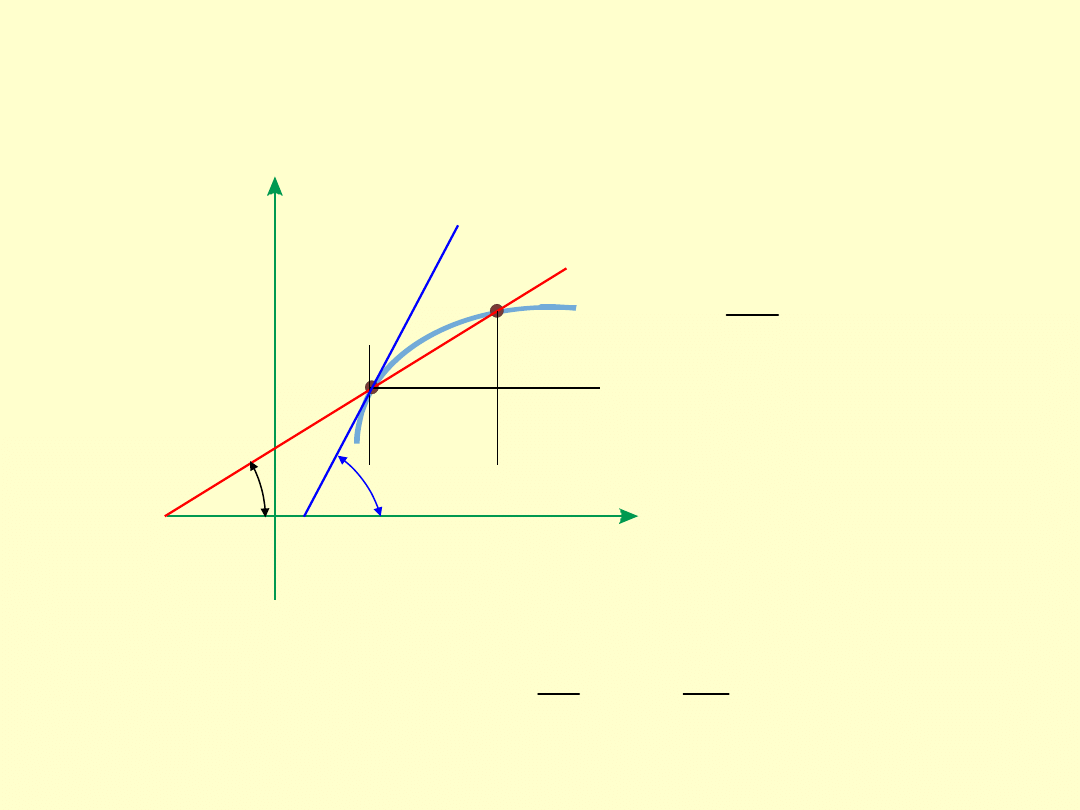
Pochodna funkcji

x

y

A(x

o

,y

o

)

B(x

1

,y

1

)

β

∆y

∆x

y

y

y

x

x

x













1

1

Pochodna funkcji

x

y

dx

dy

y

x















0

lim

α



tan



dx

dy

Pochodna funkcji w danym punkcie jest równa

współczynnikowi

kierunkowemu stycznej

do wykresu funkcji w tym punkcie.

Wyrażenie

dy = y’dx

nazywa się różniczką funkcji y = y(x),

dx

– jest różniczką

argumentu x.

2

2

dx

y

d

dx

dy

dx

d



Różniczkując pierwsza pochodną po x, otrzymamy drugą pochodną

itd……

1

0

)

(





dx

dc

c

x

y

c = const

2

dx

dy

c

dx

cy

d



)

(

3

dx

dy

dx

dy

dx

dy

y

y

y

2

1

2

1









4

dx

dy

y

y

dx

dy

dx

dy

y

y

y

2

1

2

1

2

1











Podstawowe wzory rachunku różniczkowego

5

2

2

2

1

2

1

2

1

y

dx

dy

y

y

dx

dy

dx

dy

y

y

y









6

dx

dy

dy

dz

dx

dz

x

g

y

y

f

z









)

(

),

(

Pochodna funkcji złożonej

Pochodne funkcji elementarnych

y=f(x)

y’

y=f(x)

y’

x

1

cosx

-sinx

x

n

nx

n-1

tgx

1/cos

2

x

e

x

e

x

ctgx

-1/sin

2

x

lnx

x

-1

a

x

a

x

lna

sinx

cosx

Z II zasady dynamiki, przy założeniu , wynika

- pęd ciała.

Siła działająca na ciało jest równa szybkości zmian pędu ciała.
Rozwiązując ostatnie równanie otrzymamy

Zmiana pędu ciała jest równa popędowi działającej siły

t

p

t

v

m

t

v

m

a

m

F





























)

(

t

F

p

p

t

F

p

o

























p

v

m







popęd siły

const

F 



t

F

p

p

t

F

p

o















const

F 



Jeśli

to możemy zapisać

III zasada dynamiki

Wszelkie działanie jest równe przeciwdziałaniu.

Jeżeli ciało A działa na ciało B siłą to ciało B działa na
ciało A siłą równą co do wartości, ale o przeciwnym
zwrocie

AB

F



BA

F



BA

AB

F

F









Zasada zachowania pędu

Założenia:
• układ składa się z dwóch oddziałujących ze sobą cząstek
• nie ma żadnych sił zewnętrznych działających na ten układ.
Z II zasady dynamiki wynika, że

z III zasady dynamiki





const

p

p

t

p

p

t

p

t

p





























2

1

2

1

2

1

0













t

p

F

t

p

F













2

2

1

1

,









Dopóki rozpatrujemy tylko siły

wewnętrzne

całkowity pęd układu

jest stały.

Zwiększenie

pędu jednej cząstki musi spowodować

zmniejszenie

pędu drugiej cząstki.

const

p

p

p

p

p

N

i

i

N















1

3

2

1

........











1

2

2

1

2

2

1

1

0

m

m

v

v

v

m

v

m











Uogólnienie dla układu N ciał

Napęd odrzutowy