DYNAMIKA UKŁADU PUNKTÓW MATERIALNYCH Wykład 12

Układ punktów materialnych zbiór punktów materialnych, w którym położenie każdego punktu jest zależne od położenia innych punktów.

Układ punktów swobodnych układ punktów materialnych, których ruch nie jest ograniczony żadnymi więzami.

Układ punktów nieswobodnych układ punktów

materialnych, których ruch jest ograniczony nałożonymi na te punkty więzami.

W układzie punktów materialnych występują siły wewnętrzne i zewnętrzne.

2 3 P₃

S_2,1 S_ji

S_ij

S_1,2 S_1,4 S_4,1

1 4 P₄

P₁ Rys. 23 P_i siły zewnętrzne

S_ij siły wewnętrzne S_ij = -S_ji

Z zależności S_ij = -S_ji wynika, że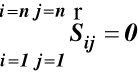
(24)

Podobnie suma momentów sił wewnętrznych względem dowolnego punktu wynosi zero, gdyż siły te parami się równoważą. Zapisujemy to wzorem

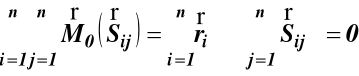
(25)

gdzie
promień wektor z m_i

S_ij

r_i z_i

x_i y

Rys.24 x y_i

Dynamiczne równanie różniczkowe ruchu i-tego

punktu materialnego ma postać

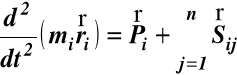
(a)

Równanie wektorowe (a) odpowiada 3 równaniom skalarnym. W przypadku n punktów mamy 3n równań różniczkowych. Rozwiązanie takiego układu równań różniczkowych jest bardzo trudne i tylko w szczególnych przypadkach można uzyskać efektywne rozwiązanie.

Środek masy punktów materialnych

Środkiem masy punktów materialnych nazywamy punkt C którego położenie w przestrzeni określa promień wektor r_C

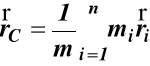
(25)

gdzie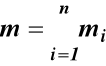

z

z_C m_n

z_i

m_i C

m₂ r_i r_C

m₃

m₁ y_i y_C y

0

x_i

x_C

x Rys.25

We współrzędnych kartezjańskich (25) ma postać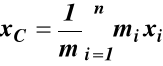


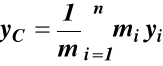
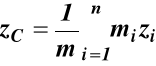
(26)

Zasady ruchu środka masy, pędu i krętu

Zsumujmy stronami równania (a), rozciągając sumowanie na wszystkie n punktów układu, w efekcie otrzymamy

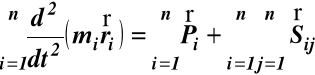
(b)

0

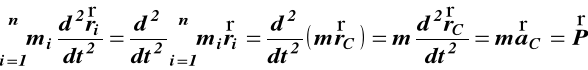
{patrz (25)}

ostatecznie

(27)

gdzie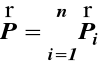
jest sumą geometryczną wszystkich sił

zewnętrznych działających na układ

Równanie (27) jest równoważne trzem równaniom skalarnym

,
,
(28)

Zasada ruchu środka masy

Środek masy każdego układu punktów materialnych porusza

się tak, jakby była w nim skupiona cała masa układu i jakby do tego punktu przyłożone były wszystkie siły zewnętrzne.

Z równania (27) wynika, że jeśli:

P = 0 to a_C = 0 czyli V_C = constans (c)

Z warunku (c) otrzymujemy: Zasadę zachowania ruchu

środka masy

Jeśli suma geometryczna sił zewnętrznych działających na dany układ punktów materialnych jest równa zeru, to środek masy pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

Przykład 13

Na końcu A stojącej nieruchomo na wodzie łódki AB o

długości b i masie M stoi człowiek, którego masa równa jest m₁ (rys.26a). Obliczyć, o ile przesunie się łódka, gdy człowiek przejdzie na drugi jej koniec (rys.26b). Przy rozwiązywaniu zadania pominąć opór wody.

a) y

S m₁

B A x

c Mg

b

b) y m₁ S

0 B A x

c Mg

x b

Rys.26

Rozwiązanie

Rozpatrywany układ materialny złożony jest z łódki i człowieka. Siły zewnętrzne tego układu to siły ciężkości Mg i m₁g oraz siły wyporu wody S.

Siła pozioma P_x = 0. Równanie (28) mamy więc postać

ponieważ Vc =
stąd x_C = const. i nie ulega zmianie

gdyż P_x = 0

Określenie położenia x_C wzór (26) w położeniu łódki z: rysunku 28a

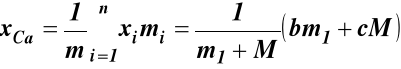
z rysunku 28b

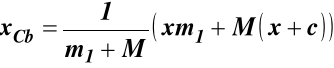
Ponieważ x_Ca = x_Cb stąd

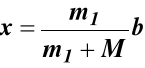
Ponieważ x>0, przeto przesunięcie łódki ma taki kierunek, jaki założony został na rys.28b.

Pęd układu punktów materialnych

Pędem układu punktów materialnych nazywamy wektorową sumę pędów wszystkich punktów materialnych tego układu

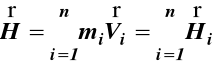
(29)

m_n

C

V_C

r_C m_i

r_i V_i

Rys.27 0 m₁

Przekształćmy (29)

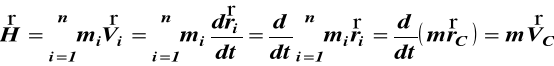
zgodnie z (25)

ostatecznie

(30)

po zróżniczkowaniu (30) otrzymujemy

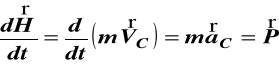
(31)

lub w postaci skalarnej

,
,
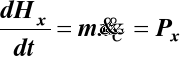
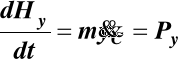
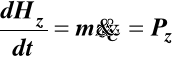
(32)

Pochodna pędu układu punktów materialnych

względem czasu jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na punkty tego układu.

Zależność (31) można przedstawić

(d)

po scałkowaniu (d) w granicach od t₁ do t₂ otrzymujemy

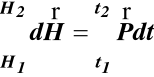
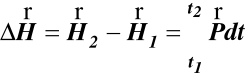
(e)

Równania (e) oznacza, że:

Przyrost pędu układu punktów materialnych jest równy popędowi sumy geometrycznej sił zewnętrznych

Zasada zachowania pędu

Jeżeli P = 0 to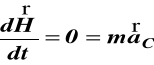
stąd

Przykład 14

Z armaty stojącej na gładkiej poziomej płaszczyźnie, wystrzelono pocisk (rys.28). W chwili opuszczania lufy prędkość pocisku V miała kierunek poziomy, a jej wartość wynosiła 300m/s. Wyznaczyć prędkość V₁, z którą armata

zacznie się cofnąć po oddaniu strzału. Masa pocisku wynosi m = 10 kg, a masa armaty M = 2000 kg. Masę gazów powstających przy wystrzale pominąć.

V₁ V

x Rys.28

Rozwiązanie

Ponieważ przed wystrzałem pęd układu był równy 0, to

stąd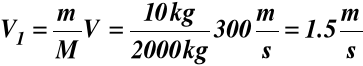

Moment pędu (kręt)

Kręt układu punktów materialnych względem dowolnego

punktu 0 (bieguna), jest to wektor równy sumie geometrycznej krętów wszystkich punktów materialnych układu względem bieguna (rys.29).

z

m_n m_i

r_i V_i

m₁ m_iV_i

K_iz

0 K_iy y

K_ix

x Rys.29

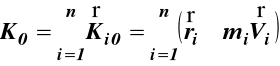
(32)

Wartości rzutów wektora krętu K₀ na osie xyz są

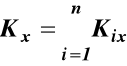
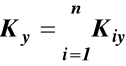
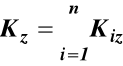
(33)

Pochodna krętu (32) ma postać

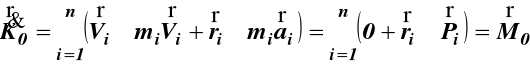
(34)

Jeśli M₀ = 0 to K₀ = const (35)

Pochodna względem czasu krętu punktów materialnych względem dowolnego punktu 0 równa jest sumie geometrycznej momentów sił zewnętrznych, jeżeli punktem 0 jest punkt nieruchomy lub środek masy układu C. (Dowód podano na str.176 kin i dyn, autor J. Misiak)

Przykład 15

Punkt materialny o masie m₁ = 2 kg porusza się z prędkością V₁ = 10 m/s po okręgu w płaszczyźnie poziomej. W pewnej chwili zderza się z drugim punktem o masie

m₂ = 3 kg, który przed zderzeniem był nieruchomy

(rys.30). Po zderzeniu oba punkty materialne są złączone i poruszają się po tym samym torze. Oblicz wspólną prędkość V₁₂ tych punktów materialnych.

m₁ V₁

m₂ m₁

V₁₂ 0

R

Rys.30

Rozwiązanie

Na podstawie zasady zachowania krętu (35)

stąd prędkość obu punktów po zderzeniu ma wartość

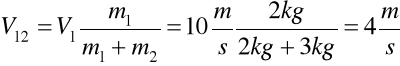
27dyn

28dyn

29dyn

30dyn

31dyn

32dyn

33dyn

34dyn

---