WIP, ID-A0-31, 11.10.2011r., 7⁴⁰-10⁰⁰

Laboratorium Podstaw Automatyki

SPRAWOZDANIE

BADANIE WŁASNOŚCI PODSTAWOWYCH ELEMENTÓW AUTOMATYKI

CEL ĆWICZENIA

Celem tego ćwiczenia jest przebadanie własności elementów automatyki bezinercyjny, inercyjny pierwszego rzędu, całkujący, różniczkujący, oscylacyjny, opóźniający.

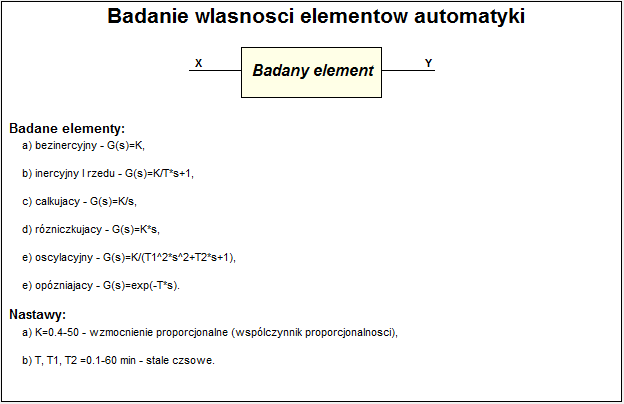
Wiele elementów automatyki można traktować jako liniowe, jeżeli ograniczy się zakres ich

pracy i przyjmie założenia upraszczające . Na przykład:
-siła tarcia jest proporcjonalna do prędkości
-sztywności elementów sprężystych są stale, a pozostałych elementów oraz ich połączeń i zamocowań nieskończenie wielkie;
- rezystancje, indukcyjności i pojemności są stałe, niezależne od prądu i napięcia.

Klasyfikuje się je wtedy najczęściej ze względu na ich własności dynamiczne.

Wyróżnimy sześć grup elementów podstawowych:

1) bezinercyjne (proporcjonalne),

2) inercyjne,

3) całkujące,

4) różniczkujące,

5) oscylacyjne,

6) opóźniające.

Każdy z tych elementów cechuje się własnym sposobem przetwarzania sygnałuy wejściowego na wyjściowy, w zależności od sposobu manipulacji współczynikiem wzmocnienia, w większości przypadków również stałych czasowych, otrzymujemy kształt sygnału wyjściowego który uzależniony jest od sposobu działania danego układu. Poniżej przebadane zostały wszystkie układy, zamieszczone wykresy prezentują działanie każdego układu z osobna, pokazując jednocześnie, wpływ stałych czasowych i współczynnika wzmocnienia na kształt wykresu tj. działania całego układu.

1. Element bezinercyjny

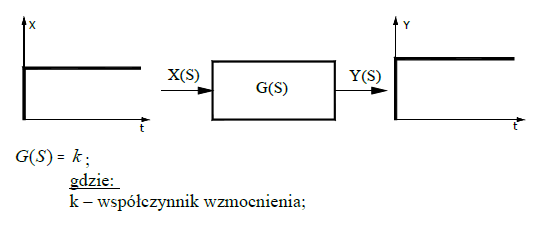
Transmitancja, czyli stosunek transformaty Laplace'a sygnału wyjściowego do transformaty sygnału wejściowego, przy zerowych warunkach początkowych, elementu bezinercyjnego jest równa współczynnikowi proporcjonalności:

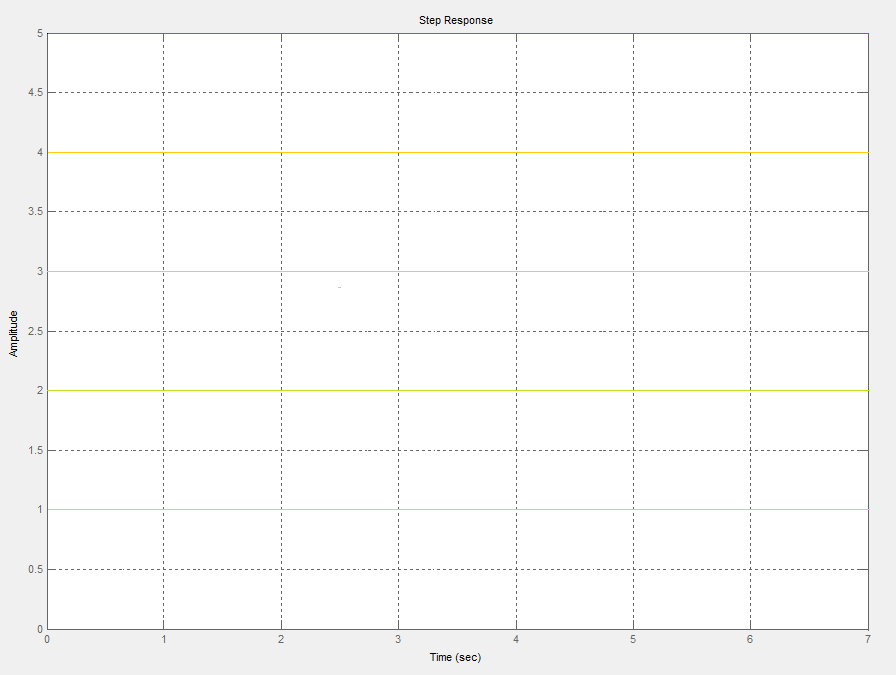
Wykresy przedstawią charakterystyki elementów bezinercyjnych dla k=1, k=2, k=3, k=4, k=5

2. Element inercyjny

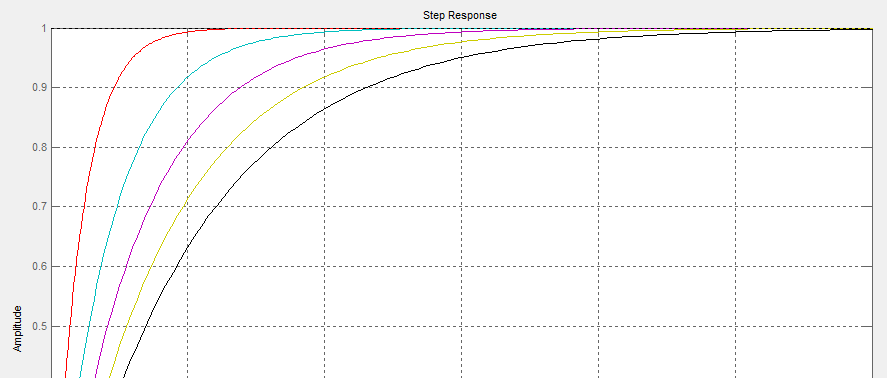
Wykresy przedstawiają charakterystyki elementów inercyjnych dla K=1 i T=1, T=2, T=3, T=4, T=5

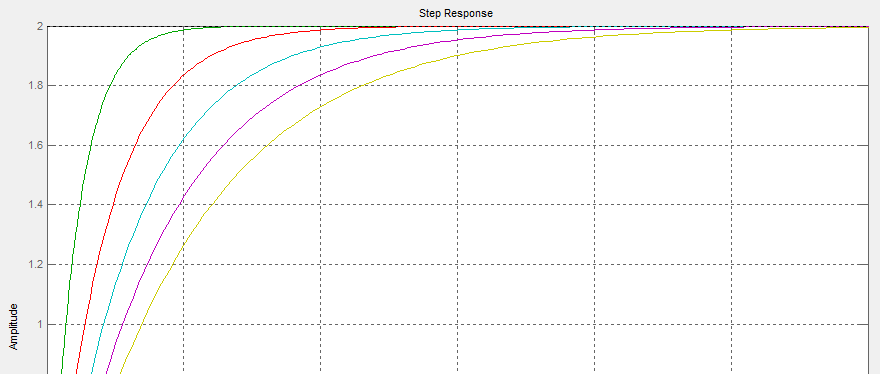
Wykresy przedstawiają charakterystyki elementów inercyjnych dla K=2 i T=1, T=2, T=3, T=4, T=5

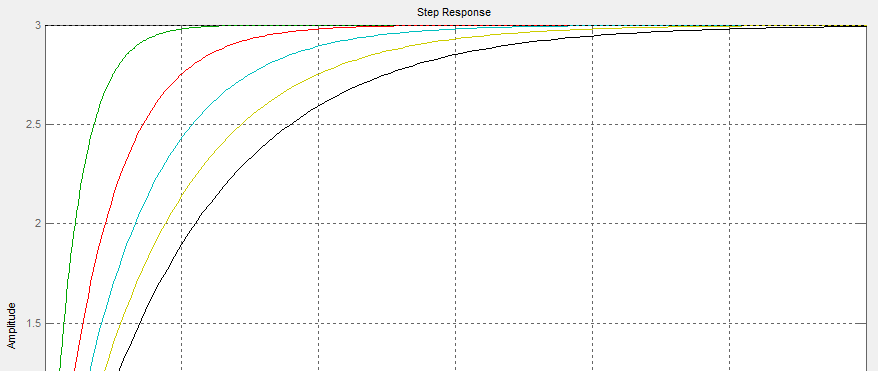
Wykresy przedstawiają charakterystyki elementów inercyjnych dla K=3 i T=1, T=2, T=3, T=4, T=5

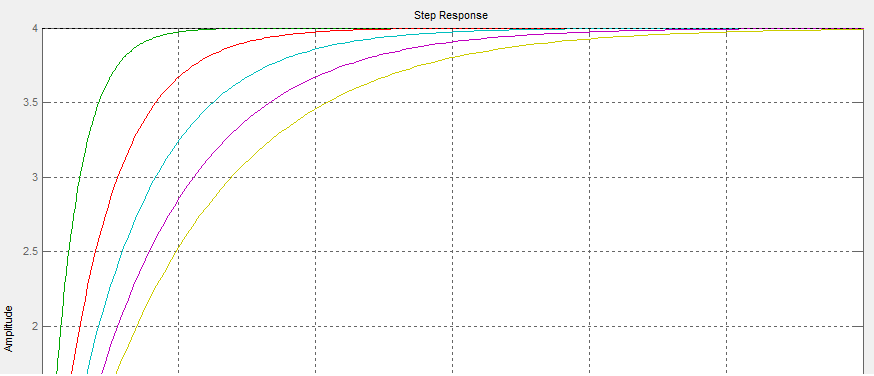
Wykresy przedstawiają charakterystyki elementów inercyjnych dla K=4 i T=1, T=2, T=3, T=4, T=5

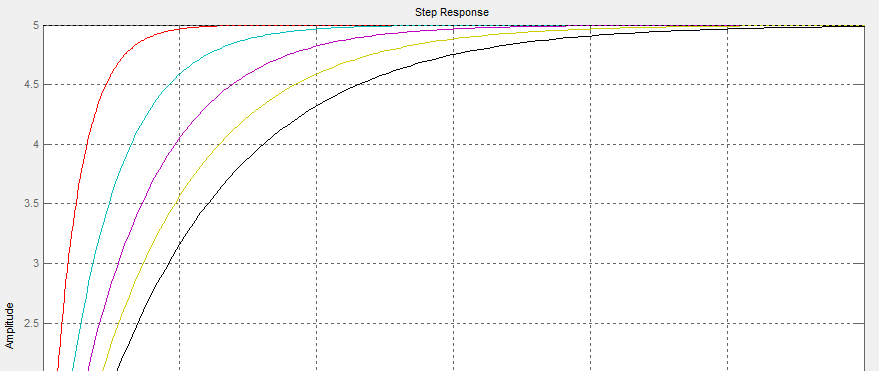
Wykresy przedstawiają charakterystyki elementów inercyjnych dla K=1 i T=1, T=2, T=3, T=4, T=5

3. Element całkujący

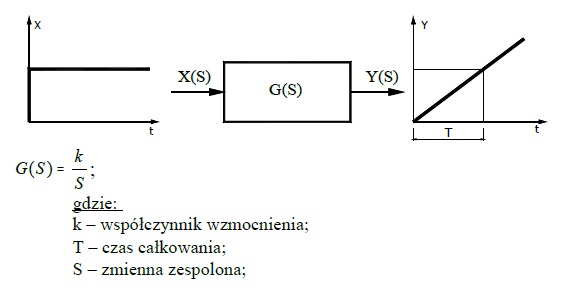
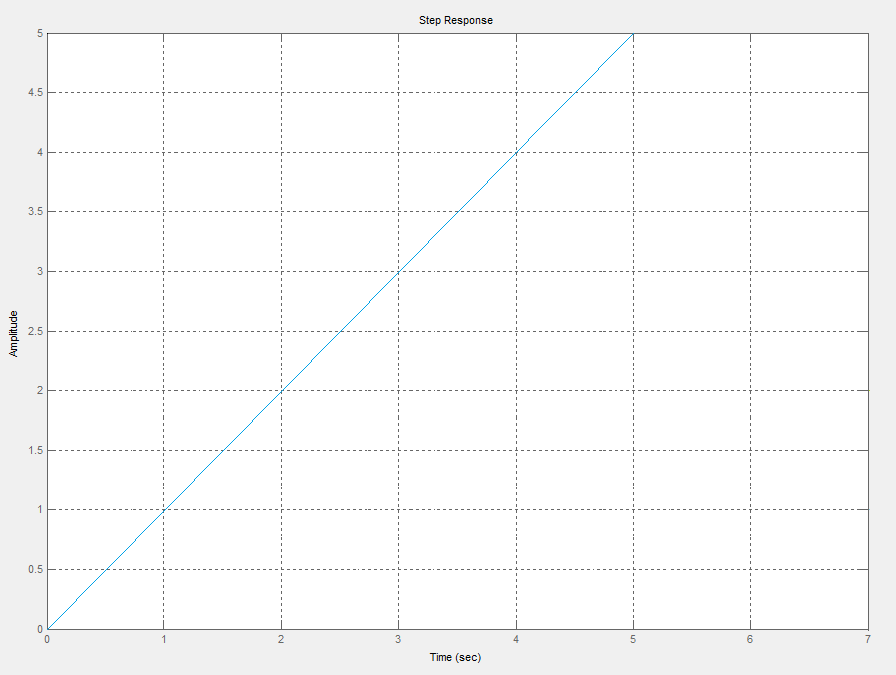
Wykresy przedstawiają charakterystyki elementów inercyjnych dla K=5 i T=5

4. Element różniczkujący

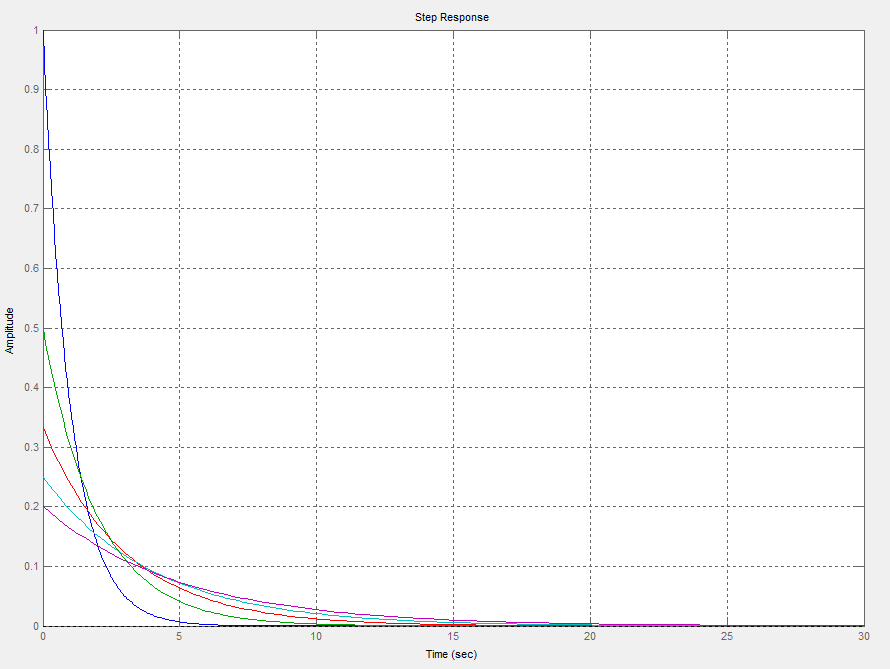
Wykresy przedstawiają charakterystyki elementów różniczkujących dla K=1 i T=1, T=2, T=3, T=4, T=5

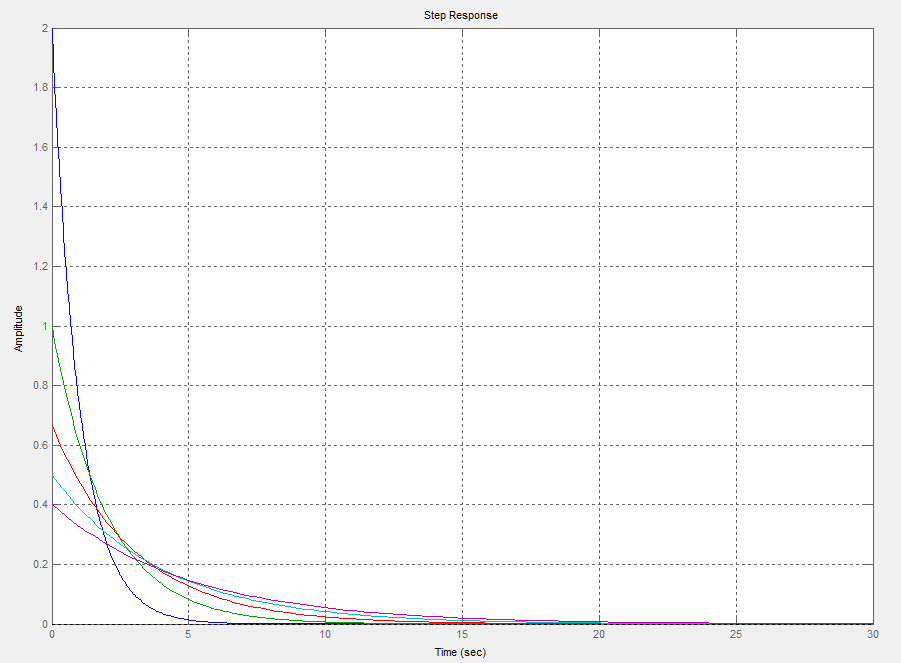
Wykresy przedstawiają charakterystyki elementów różniczkujących dla K=2 i T=1, T=2, T=3, T=4, T=5

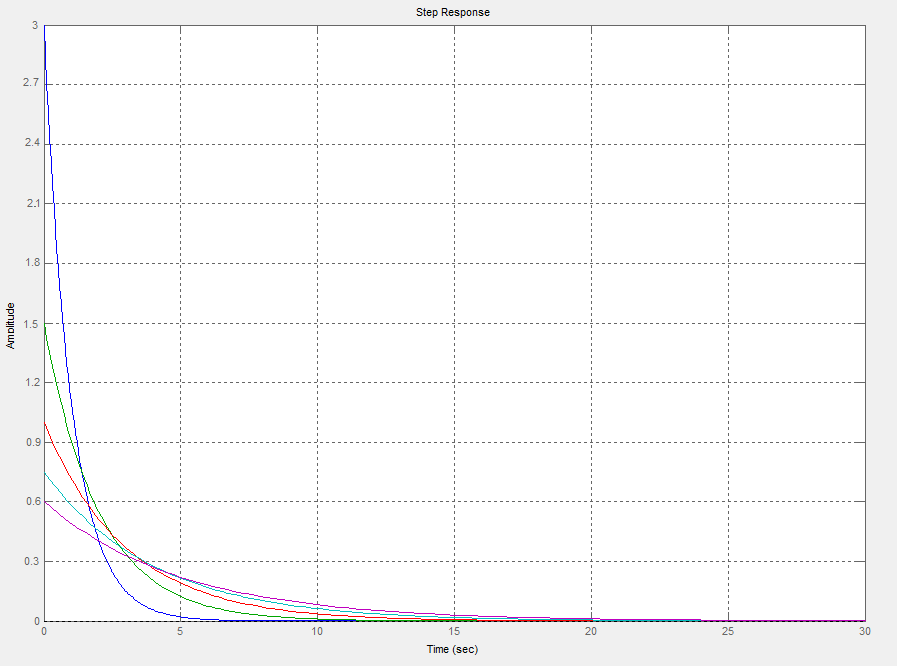
Wykresy przedstawiają charakterystyki elementów różniczkujących dla K=3 i T=1, T=2, T=3, T=4, T=5

Wykresy przedstawiają charakterystyki elementów różniczkujących dla K=4 i T=1, T=2, T=3, T=4, T=5

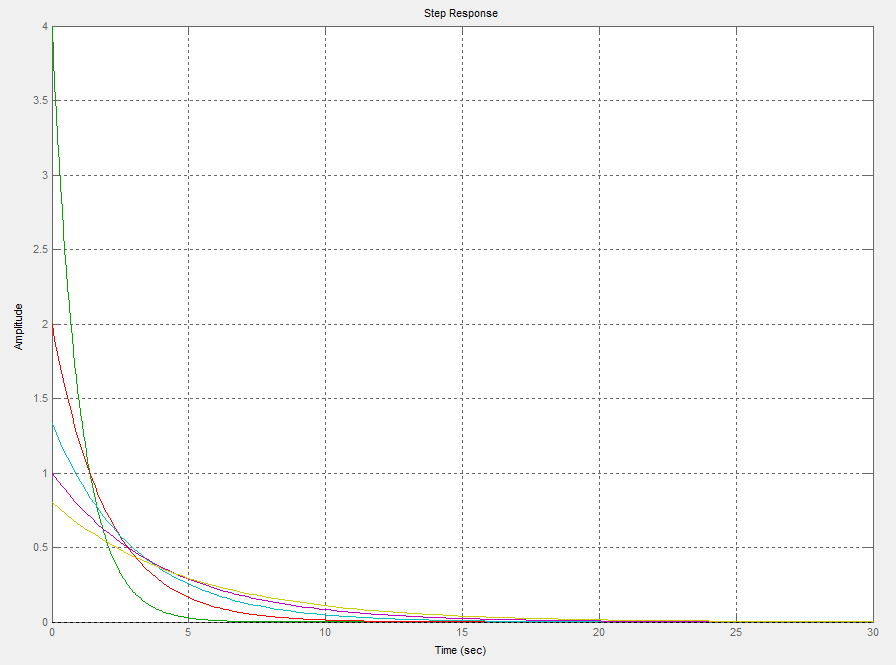
Wykresy przedstawiają charakterystyki elementów różniczkujących dla K=5 i T=1, T=2, T=3, T=4, T=5

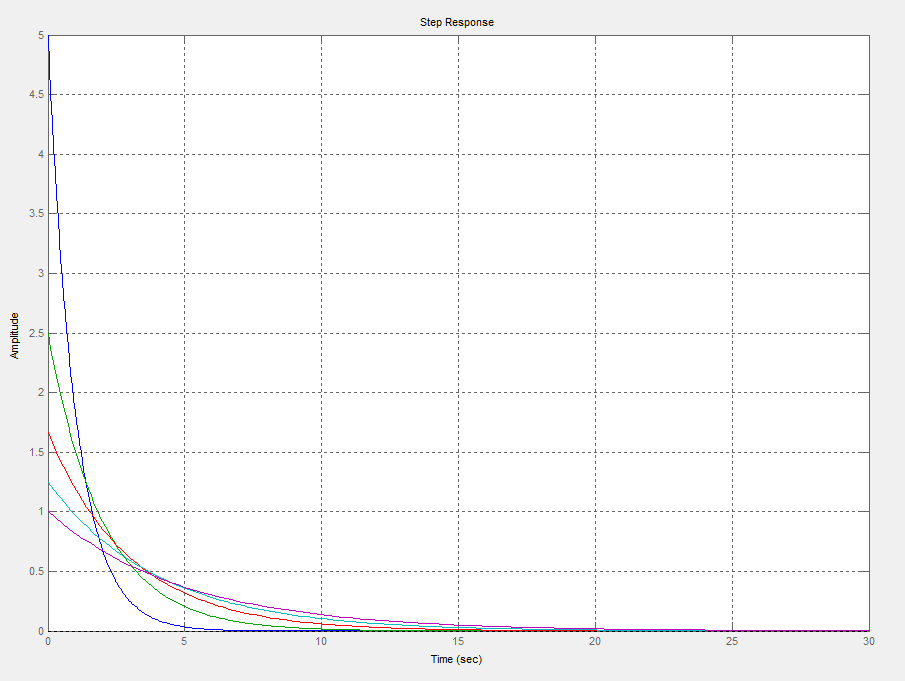
5. Element oscylacyjny

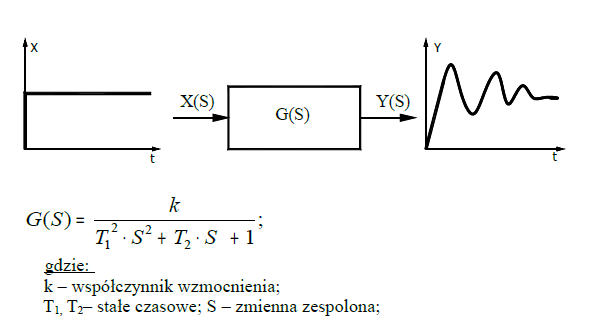
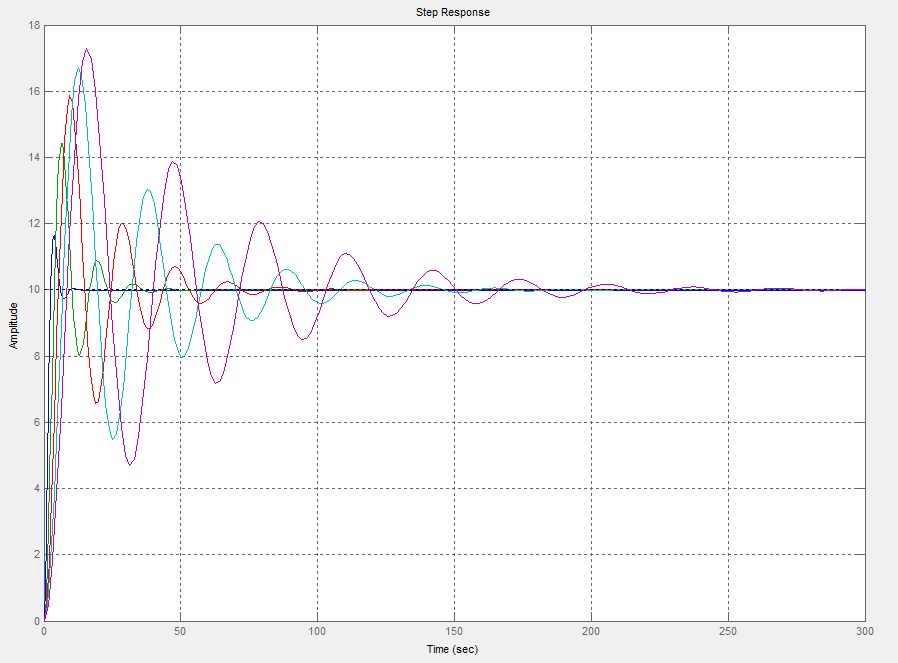
Wykresy przedstawiają charakterystyki elementów oscylujących dla K=10 i T₁=1, T₁=2, T₁=3, T₁=4, T₁=5, T₂=1

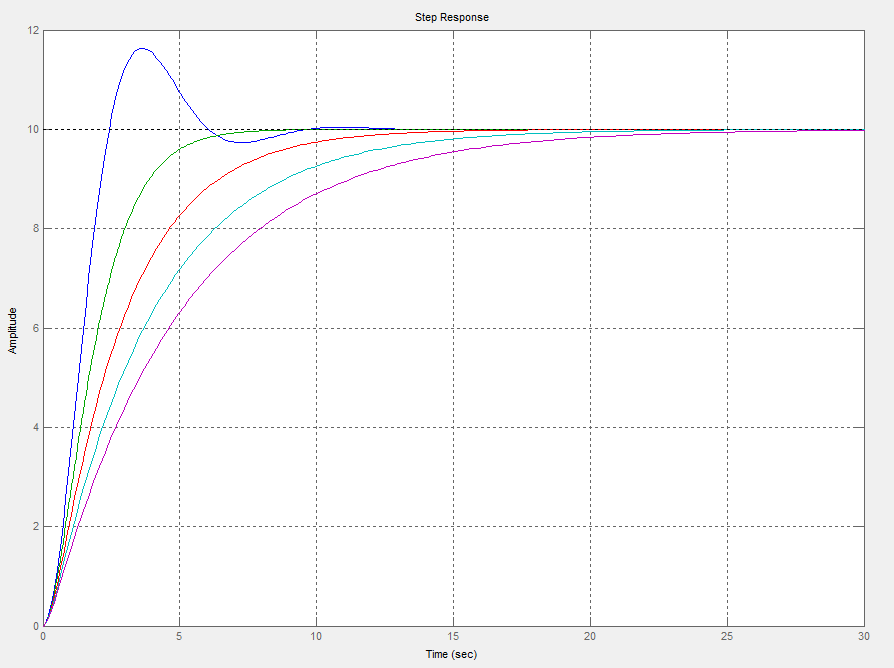
Wykresy przedstawiają charakterystyki elementów oscylujących dla K=10 i T₁=1, T₂=1 T₂=2, T₂=3, T₂=4, T₂=5

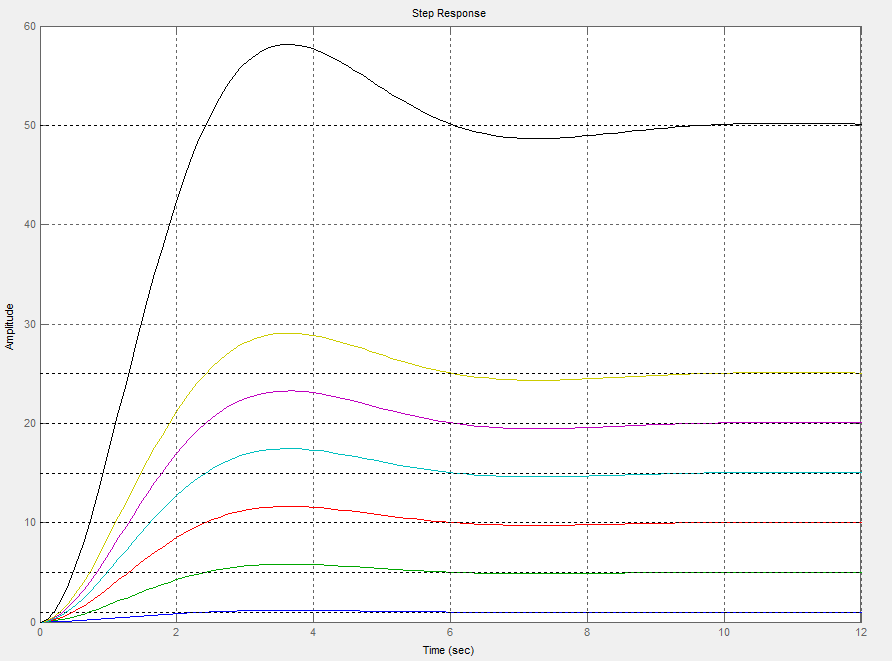
Wykresy przedstawiają charakterystyki elementów oscylujących dla K=1-50 i T₁=1, T₂=1

6. Element opóźniający

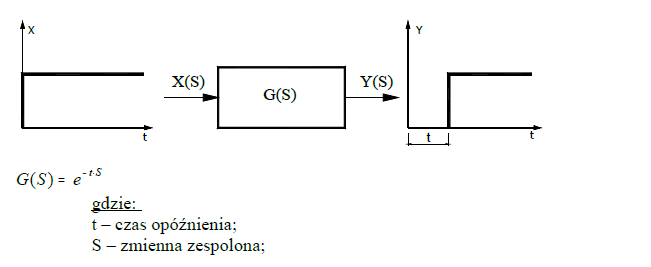
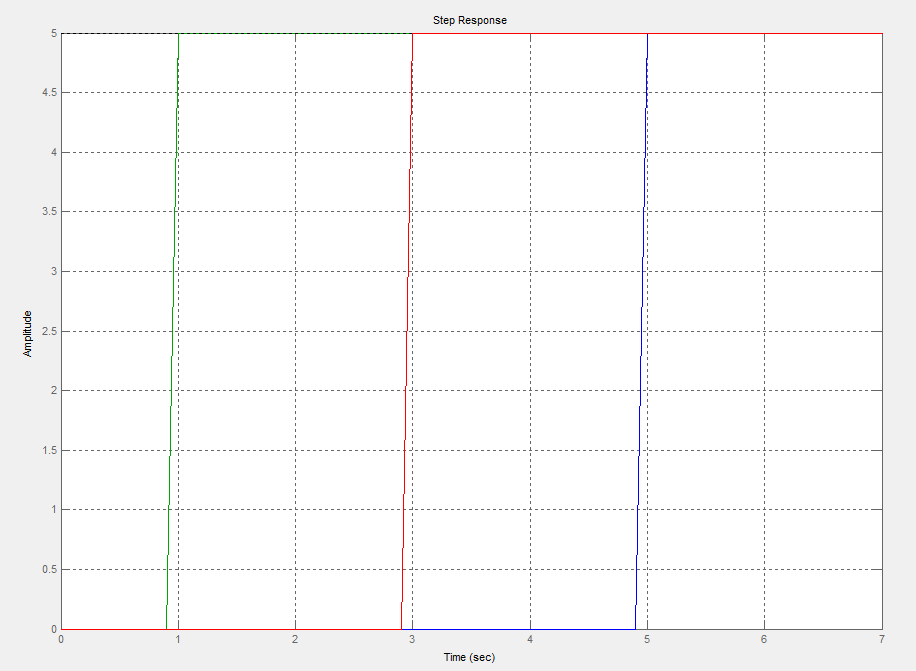
Wykresy przedstawiają charakterystyki elementów opóźniających dla T=1, T=3, T=5

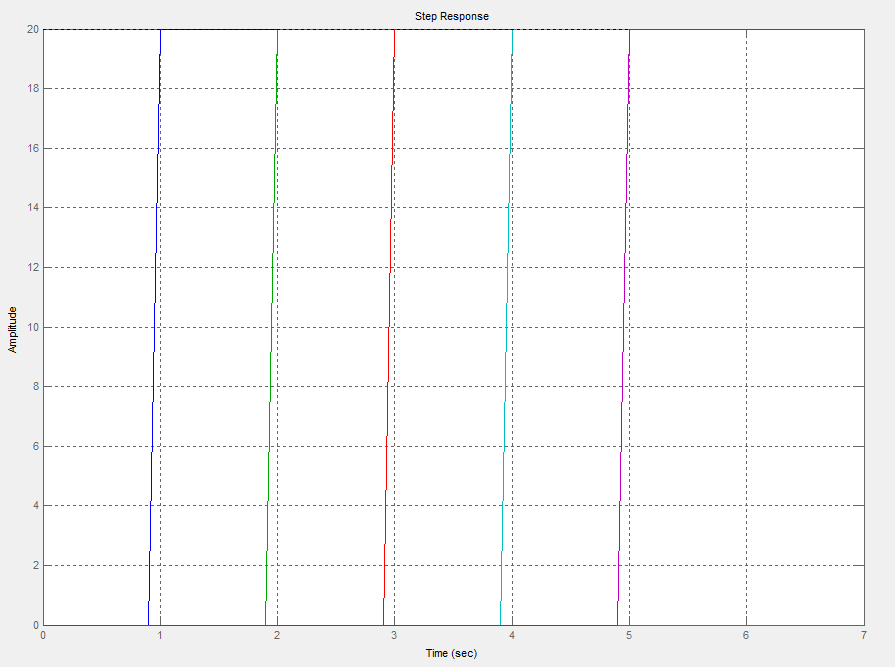
Wykresy przedstawiają charakterystyki elementów opóźniających dla T=1, T=2, T=3, T=4, T=5

Wnioski:

- W układach bezinercyjnych widzimy, że sygnał wyjściowy jest stricte uzależniony od współczynnika wzmocnień, co doskonale obrazuje funkcja przedstawiająca system działania tego układu.

- W układach inercyjnych sygnał wyjściowy w zależności od stałej czasowej, szybciej (wraz z jej spadkiem) uzyskuje maksymalny pułap. Współczynnik wzmocnień nie ma dużego wpływu na amplitudę poza zwiększeniem jej.

- W elementach różniczkujących wraz ze wzrostem współczynnika wzmocnienia rośnie także amplituda. Wraz ze wzrostem parametru T₁ zmniejsza się amplituda, ale wydłuża się czas po którym wykres dochodzi do poziomu 0.

- W elementach opóźniających zmieniając zmienną T₁ ustawią się czas po którym następuję wzmocnienie sygnału. Swoiste opóźnienie sygnału.

- W elementach oscylacyjnych wraz ze wzrostem współczynnika wzmocnienia rośnie także amplituda. Zwiększając parametr T₁ zwiększa się także amplituda wykresu oraz wydłuża się czas po którym wykres się stabilizuje. Zmiana parametru T₂ powoduje zmniejszenie się amplitudy, ale czasu ulega wydłużeniu.

- Dzięki MATLAB'owi mogliśmy zbadać każdy układ z osobna i zobaczyć zobrazowany schemat ich funkcjonowania w praktyce. Pozwala nam to dobrać idealnie układ, który spełnia nasze potrzeby i będzie realizował powierzone mu funkcje, w układach automatyki, w stu procentach.

---