1. Iloczyn skalarny i wektorowy +przykłady wielkości fizycznych skalarnych i wektorowych

2. Różniczka zupełna w rachunku błędu

3. Ruch punktu materialnego

4. Ruch jednostajny po okręgu

5. Pęd i zasada zachowania pędu

6. Praca i moc mechaniczna + przykłady

7. Zasady dynamiki Newtona, siły bezwładności

8. Drgania harmoniczne prostej tłumionej

9. Równanie płaskiej fali harmonicznej , wielkości opisujące ruch falowy

10. Zjawisko falowe

11. Moment siły, moment pędu, moment bezwładności, twierdzenie Steinera

12. Gaz doskonały , równanie stanu gazu doskonałego

13. Zasady termodynamiki

14. Pole elektrostatyczne + parametry

15. Model pasmowy przewodnictwa

16. Mechanizmy oporności elektrycznej

17. Model atomu według Bohra

18. Fotoefekt zewnętrzny

19. Efekt Comptona

20. Promieniowanie Rentgenowskie

21. Dualizm korpuskularno-falowy

22. Teoria de Broglie

23. Zasada nieoznaczoności Heisenberga

AD . 1

Iloczyn skalarny - operator na przestrzeni liniowej przypisujący dwóm argumentom z tej przestrzeni rzeczywistą wartość skalarną. Jest to standardowy iloczyn skalarny określony w przestrzeni euklidesowej i bywa tak określany. Niżej przez iloczyn skalarny rozumie się dokładnie ten standardowy iloczyn skalarny.

Skalar - w algebrze (liniowej) element ustalonego ciała nad którym zbudowany jest dowolny moduł (przestrzeń liniowa).

W fizyce iloczyn skalarny jest w powszechnym użyciu, co wynika bezpośrednio z faktu, że zarówno w fizyce klasycznej jak i kwantowej matematyczną podstawę stanowią przestrzenie liniowe z określonym iloczynem skalarnym, przykładami mogą być:

• trójwymiarowa przestrzeń euklidesowa
  

• przestrzeń Hilberta w mechanice kwantowej
  

Iloczyn wektorowy to działanie (n − 1)-argumentowe na elementach n-wymiarowej przestrzeni euklidesowej.

Wartość iloczynu wektorowego jest równa iloczynowi długości pierwszego wektora przez długość rzutu drugiego wektora na kierunek prostopadły do pierwszego wektora.

Długość wektora otrzymanego jako iloczyn wektorowy dwóch wektorów jest równa polu równoległoboku rozpiętego na tych wektorach.

Wektor zerowy otrzymamy, gdy jeden z wektorów wyjściowych jest zerowy lub gdy wyjściowe wektory są równoległe.

AD.2

Różniczką zupełną funkcji P(q₁,q₂,...,q_n) nazywamy takie wyrażenie Pfaffa, że:

gdzie:

- pochodna cząstkowa funkcji P po zmiennej q_i

AD 3.

Punkt materialny (masa punktowa) to ciało fizyczne obdarzone masą, ale mające tak małe rozmiary, że w opisie matematycznym zjawiska dane ciało można potraktować jak punkt geometryczny. W zależności od problemu, jako punkt materialny można traktować:

• elektron krążący po orbicie wokół jądra.

- kamień rzucony pod pewnym kątem do powierzchni Ziemi - jego rozmiary są nieistotne w porównaniu z odległością jaką przebędzie i dokładnością pomiarów.

- Ziemia poruszająca się po orbicie wokół Słońca - jej wymiary są nieistotne w porównaniu z promieniem orbity.

Redukcja ciała do punktu materialnego ma istotne znaczenie dla prostoty opisu ruchu danego ciała. Masa punktowa w fizyce to idealizacja ciała lub układu ciał, w której wymiary układu można pominąć w porównaniu z odległościami, które pokonuje. Wtedy można przyjąć, że cała masa układu jest skupiona w środku masy układu. W przypadku jednorodnego ciała kulistego, jeżeli nie obraca się ono, masa punktowa jest nie tylko idealizacją, ponieważ takie ciało zachowuje się tak jak masa punktowa.

• Prawa ruchu punktu materialnego mającego masę równą masie ciała sztywnego są identyczne z ruchem jednego punktu związanego z ciałem. Punkt ten nazywany jest środkiem masy. Masa punktowa ma nieskończoną gęstość.

• Źródło: "http://pl.wikipedia.org/wiki/Punkt_materialny"

AD 4.

Ruch jednostajny po okręgu - ruch po torze o kształcie okręgu z prędkością o stałej wartości, tzn.
. Ruch jednostajny po okręgu jest ruchem niejednostajnie przyspieszonym, tzn. kierunek i zwrot wektorów przyspieszenia
i prędkości
zmieniają się cały czas w trakcie ruchu, nie zmieniają się natomiast ich wartości.

Ruch jednostajny po okręgu może być także definiowany jako ruch po okręgu ze stałą prędkością kątową

Ad 5.

Zasada zachowania pędu mówi, że dla dowolnego izolowanego układu punktów materialnych, bez względu na to, jakie jest oddziaływanie między nimi, suma wektorowa wszystkich pędów pozostaje stała. Przejawem działania tej zasady jest zjawisko odrzutu, polegające na tym, że przy rozpadzie ciała na dwie części obie otrzymują pędy jednakowe co do wartości bezwzględnej, lecz przeciwnie skierowane względem układu odniesienia, w którym ciało przed rozpadem pozostawało w spoczynku. Przykładem mogą być odrzuty przy strzelaniu z broni palnej, przy emisji cząsteczek z jądra atomowego itp. Na tej podstawie działają też samoloty odrzutowe oraz rakiety, gdzie pęd strumienia gazów wyrzucanych z dyszy nadaje samolotowi lub rakiecie pęd w kierunku przeciwnym.

Matematyczne sformułowanie zasady zachowania pędu:

Pęd - w mechanice wielkość fizyczna opisująca ruch ciała. Pęd mają wszystkie formy materii, np. ciała obdarzone masą, pole elektromagnetyczne, pole grawitacyjne.

AD 6.

Praca (W) - jest sposobem przekazywania energii na drodze mechanicznej jednemu ciału (lub układowi ciał) przez drugie.

Praca jest wielkością skalarną zdefiniowaną jako iloczyn skalarny wektora siły przez wektor zmiany położenia:

W = F × Dr = F × Dr × cos(F,Dr)

Praca w ujęciu fizycznym ma wartość dodatnią, jeżeli spowoduje przyrost energii układu nad którym ta praca została wykonana.

Moc (P) - skalarna wielkość fizyczna, która informuje nas o szybkości wykonywanej pracy.

Np. 100 km/h

Praca przykład np. Przesunięcie pudełka o 2 metry itp…

Moc. Szybkośc z jakoą wykonaliśmy przesunięcie tego pudełka.

AD 7.

Zasady dynamiki Newtona

I zasada dynamiki (zasada bezwładności)

Jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

( Philosophiae Naturalis Principia Mathematica, 1726 edition)

Lex I. Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.

Każde ciało trwa w swym stanie spoczynku lub ruchu prostoliniowego jednostajnego, jeżeli siły przyłożone nie zmuszą ciała do zmiany tego stanu.

O takim ruchu mówimy czasem jako o ruchu swobodnym.

Wybierzmy ciało spełniające założenia pierwszej zasady dynamiki i odnieśmy (ciało jest układem odniesienia) ruch innego ciała, na które też nie działa żadna siła wówczas ciało to spoczywa lub porusza się po linii prostej ruchem jednostajnym względem wybranego ciała (układu odniesienia). Takie układy odniesienia nazywamy układami inercjalnymi.

Dlatego pierwsza zasada dynamiki jest traktowana jako postulat istnienia inercjalnego układu odniesienia i jest formułowana:

Istnieje układ odniesienia, w którym ciało nie podlegające oddziaływaniom zewnętrznym spoczywa lub porusza się po prostej ze stałą prędkością.

Jeżeli istnieje jeden inercjalny układ odniesienia, to istnieje ich nieskończenie wiele. Układy inercjalne spoczywają lub poruszają się względem siebie po linii prostej ze stałą prędkością.

Wyżej opisany sposób zamiany opisu ruchu z jednego układu odniesienia do innego w mechanice klasycznej nazywany jest transformacją Galileusza

Bezwładność ciał jest to zdolność ciał do przeciwstawiania się wszelkim zmianom ruchu. Miarą bezwładności jest jego masa.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa)

Współczynnik proporcjonalności jest równy odwrotności masy ciała.

W wersji oryginalnej

W wersji oryginalnej

Lex II. Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.

''Zmiana ruchu jest proporcjonalna do przyłożonej siły poruszającej i odbywa się w kierunku prostej, wzdłuż której siła jest przyłożona.''

W wersji zwanej uogólnioną (uogólniona druga zasada dynamiki), obowiązuje dla ciała o zmiennej masie np w mechanice relatywistycznej:

Zmiana pędu ciała jest proporcjonalna do działającej siły wypadkowej.

Przy prędkościach, w których nie występują efekty relatywistyczne czyli dla prędkości znacznie mniejszych od prędkości światła, zasadę tę można wyrazić w wersji uproszczonej (ta wersja funkcjonuje na wstępnych etapach nauczania fizyki i jest stosowana powszechnie do obliczeń):

Przyspieszenie z jakim porusza się ciało jest proporcjonalne do działającej siły a odwrotność masy jest współczynnikiem proporcjonalności. Kierunek i zwrot przyspieszenia jest zgodny z kierunkiem i zwrotem siły.

Siła bezwładności (siła inercji) to wyimaginowana, pozorna siła nie pochodząca od żadnego ciała, będąca wynikiem przyspieszenia układu odniesienia (czyli układu nieinercjalnego). Siła bezwładności nie jest siłą, gdyż definicja tej wartości nie jest do końca zgodna z pierwotnym założeniem I zasady dynamiki Newtona. Nazwa wzięła się stąd iż siła ma swój efekt, w niektórych układach nieinercjalnych można zauważyć efekt typowy dla dziania siły (np. przemieszczenie), jednakże dziejący się bez działania tej siły.

AD 8.

Ruch harmoniczny drgania opisane funkcją harmoniczną (sinusoidalną), jest to najprostszy w opisie matematycznym rodzaj drgań.

Ruch harmoniczny jest często spotykanym rodzajem drgań, wiele rodzajów jest w przybliżeniu harmoniczna. Każde drganie można przedstawić jako sumę drgań harmonicznych. Przekształceniem umożliwiającym rozkład ruchu drgającego na drgania harmoniczne jest transformacja Fouriera.

Ruch harmoniczny tłumiony występuje wtedy, gdy na ciało działa dodatkowo siła oporu ośrodka proporcjonalna do prędkości:

Równanie ruchu ma wtedy postać:

Równanie to ma dwie klasy rozwiązań:

Oscylator przetłumiony

Gdy:

odpowiada to tak zwanemu oscylatorowi przetłumionemu - w tej sytuacji nie występuje ruch okresowy, a jedynie eksponencjalny zanik wychylenia z czasem.

Oscylator drgający [edytuj]

Gdy

ω₀ > b

AD 9.

Fala harmoniczna - fala pobudzająca cząstki ośrodka do drgań harmonicznych. Położenie punktu ośrodka zmienia się sinusoidalnie w czasie:

gdzie:

• x - wychylenie z położenia równowagi wybranego punktu

• A - amplituda fali, największe wychylenie

• ωt - faza drgań

• ω - częstotliwość (pulsacja)

• φ - faza początkowa drgań

• T- okres, czas trwania jednego pełnego drgania

• f- częstotliwość, liczba drgań w jednej sekundzie.

AD 10.

Zjawisko Falowe

Fala to zaburzenie, które się rozprzestrzenia. Fale przenoszą energię z jednego miejsca do drugiego bez transportu jakiejkolwiek materii. W przypadku fal mechanicznych cząsteczki ośrodka, w którym rozchodzi się fala, oscylują wokół położenia równowagi.

Charakterystyczne własności

Wszystkie fale wykazują następujące własności:

• odbicie - na granicy ośrodków fale zmieniają kierunek bez zmiany ośrodka

• załamanie - na granicy ośrodków fala przechodząc do drugiego ośrodka zazwyczaj zmienia kierunek swego ruchu

• dyfrakcja - zdolność do omijania przeszkód mniejszych niż długość fali, oraz powstawanie pasków dyfrakcyjnych na szczelinie albo wąskiej przeszkodzie

• interferencja - nakładanie się fal z różnych źródeł może doprowadzić do ich wzmocnienia lub wygaszenia

• rozszczepienie - załamanie fal zależne od ich długości powoduje rozkład fali na fale składowe, np. na pryzmacie

AD 11.

Moment siły, wektor osiowy D=r×F, gdzie: r - promień wodzący zaczepiony w pewnym wybranym punkcie (względem tego punktu wyznacza się moment siły), F - wektor działającej siły, znak × oznacza iloczyn wektorowy. Wypadkowy moment siły działający na ciało równy jest ich sumie wektorowej.

Skutkiem działania na ciało wypadkowego niezerowego momentu siły jest ruch obrotowy (D=dJ/dt, gdzie: J moment pędu).

Moment pędu, kręt, wektor osiowy J charakteryzujący ruch ciała (w szczególności ruch obrotowy): J=r×p (iloczyn wektorowy wektora wodzącego r i pędu ciała).

Dla układu ciał moment pędu układu jest sumą wektorową momentu pędu pojedynczych ciał, dla ciała o ciągłym rozkładzie masy moment pędu wyraża się wzorem:

Moment bezwładności to miara bezwładności ciała w ruchu obrotowym. Im większy moment, tym trudniej zmienić ruch obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość obrotową.

gdzie:

• m - masa fragmentów ciała oddalonych od osi obrotu o długość r

• r - odległość fragmentów ciała od jego osi obrotu

Bezwładność - właściwość wszystkich ciał materialnych, polegająca na tym, że w inercjalnym układzie odniesienia, jeśli na ciało nie działa siła lub działające siły równoważą się, to porusza się ono bez przyspieszenia lub spoczywa

Twierdzenie Steinera - twierdzenie mechaniki oraz wytrzymałości materiałów opisujące sposób znajdowania momentu bezwładności danej bryły względem danej osi przy danym momencie bezwładności względem osi równoległej i przechodzącej przez środek masy bryły. Jego autorem jest Jakob Steiner. Wynika ono z wpływu przesunięcia osi na momenty bezwładności i zboczenia (dewiacji, odśrodkowy), przy czym zakładamy że początek układu współrzędnych pokrywa się ze srodkiem masy ciała, więc pomijamy moment statyczny.

AD 12.

Gaz doskonały - zwany gazem idealnym jest to abstrakcyjny, matematyczny model gazu, spełniający następujące warunki:

- brak oddziaływań międzycząsteczkowych z wyjątkiem odpychania w momencie zderzeń cząsteczek

- objętość cząsteczek jest znikoma w stosunku do objętości gazu

- zderzenia cząsteczek są doskonale sprężyste

- cząsteczki znajdują się w ciągłym chaotycznym ruchu

Gaz taki w mechanice klasycznej opisuje równanie Clapeyrona (równanie stanu gazu doskonałego), przedstawiające zależność między ciśnieniem gazu (p), jego objętością (V), temperaturą (T) i licznością (n) wyrażoną w molach:

 gdzie  R jest stałą gazową

Lub

 gdzie  k jest stałą Boltzmanna.

Gaz doskonały to model, słuszny w pełni jedynie dla bardzo rozrzedzonych gazów. Wzrost ciśnienia powoduje, że zmniejszają się odległości między cząsteczkami oraz powoduje pojawianie się oddziaływań międzycząsteczkowych. Oddziaływania te występują też blisko temperatury skraplania. W bardzo wysokich temperaturach zderzenia przestają być sprężyste. Model ten może być jednak stosowany w praktyce do niemalże wszystkich gazów w warunkach normalnych. Dla gazów rzeczywistych przy dużych gęstościach i ciśnieniach niezbędne jest stosowanie równań uwzględniających te efekty (zob. równanie Van der Waalsa i wirialne równanie stanu).

AD 13.

Zasady Termodynamiki, podstawowe prawa przyrody rządzące procesami zachodzącymi w układach termodynamicznych:

1) pierwsza zasada termodynamiki - zmiana energii wewnętrznej układu równa jest sumie ciepła dostarczonego do układu i pracy wykonanej nad układem. Zasada ta, równoważna zasadzie zachowania energii, w zarysach sformułowana została w 1842 przez J.R. Mayera, uściślona zaś w 1847 przez H.L.F. de Helmholtza.

2) druga zasada termodynamiki - istnieje entropia będąca funkcją stanu układu, stałą w odwracalnych procesach adiabatycznych i rosnącą we wszystkich innych. Zasadę tę, zgodnie z którą kierunek wzrostu entropii może służyć do formalnego wyróżnienia kierunku upływu czasu (wszystkie inne prawa fizyki klasycznej nie ulegają zmianie przy zamianie przyszłości z przeszłością), podał w 1850 R.J.E. Clausius, a uściślił w 1851 Kelvin lord of Largs.

3) trzecia zasada termodynamiki - entropia układu o ustalonych parametrach (np. o stałym ciśnieniu lub objętości) i temperaturze zmierzającej do zera bezwzględnego zmierza również do zera. Zasadę tę, pozwalającą obliczyć bezwzględną wartość entropii (określanej przedtem tylko z dokładnością do stałej), podał w 1906 W.H. Nernst (tzw. twierdzenie Nernsta).

Niekiedy nazwą czwartej zasady termodynamiki określa się twierdzenie Onsagera, a za zasadę tzw. zerową uznaje się twierdzenie głoszące, że dwa ciała będące w równowadze termodynamicznej z pewnym układem są w równowadze termodynamicznej ze sobą.

AD 14.

Jeśli przestrzeńma taką cechę, że na umieszczony w niej ładunek działa siła elektryczna, to w przestrzeni tej istnieje pole elektryczne.
Źródłem pola są ładunki elektryczne. Ładunki spoczywające wytwarzają pole elektrostatyczne.

Rodzaje pól:
1) centralne- wytworzone przez ładunek punktowy. Linie pola rozchodzą się promieniście (zwrot od + do -)

---<<--- + --->>--- ----->>--- - ---<<------
2) jednorodne (stałe). Linie pola są do siebie równoległe.

+ --------------->>>>>>>------------ -
+ --------------->>>>>>>------------ -
+ --------------->>>>>>>------------ -
+ --------------->>>>>>>------------ -

Wielkości charakteryzujące pole elektro statyczne:

Natężenie pola elektrostatycznego w danym punkcie pola to stosunek siły, jaka działa na dodatni (próbny) ładunek umieszczony w tym punkcie, do wartości tego ładunku.

E-natężenie
q-ładunek E=F/q E- natężenie E jest wielkością wektorową
F- siła

Napięcie elektryczne między dwoma punktami pola określamy jako stosunek pracy, jaką wykonało pole, przesuwając ładunek między tymi punktami, do wartości tego ładunku

U-napięcie
W-praca U=W/q U- napięcie jest wielkością skalarną
q-ładunek

AD 15.

Pasmowa teoria przewodnictwa elektrycznego - kwantowomechaniczna teoria opisująca przewodnictwo elektryczne. W przeciwieństwie do teorii klasycznej punktem wyjścia w tej teorii jest statystyka Fermiego-Diraca i falowa natura elektronów. Najważniejszym pojęciem tej teorii jest pasmo energetyczne - jest to przedział energii, jaką mogą posiadać elektrony w przewodniku. Istnienie ciągłego widma energetycznego jest związane z oddziaływaniem na siebie poszczególnych atomów (jest to zbiór bardzo blisko położonych widm liniowych), natomiast występowanie obszarów zabronionych wynika z warunków nakładanych na periodyczność funkcji falowej elektronów.

AD 16.

Rezystywność (oporność właściwa) to miara oporu z jakim materiał o danych wymiarach przeciwstawia się przepływowi prądu elektrycznego.

Rezystywność jest zazwyczaj oznaczana jako ρ (mała grecka litera rho).

Jednostką rezystywności w układzie SI jest om⋅metr (1 Ωm).

Odwrotność rezystywności to konduktywność.

Rezystywność określa wzór na zależność rezystancji przewodnika od jego wymiarów:

Z czego wynika:

,

Rezystywność jest wielkością charakterystyczną dla substancji w danej temperaturze.

W ogólności rezystywność metali wzrasta wraz z temperaturą, a rezystywność półprzewodników zmniejsza się przy wzroście temperatury.

Rezystywność niektórych substancji w niskich temperaturach znika całkowicie; zjawisko to nazywa się nadprzewodnictwem.

AD 17.

Model budowy atomu Bohra - model atomu wodoru autorstwa Nielsa Bohra. Bohr przyjął wprowadzony przez Ernest Rutherforda model atomu, według tego modelu elektron krąży wokół jądra jako naładowany punkt materialny, przyciągany do jądra siłami elektrostatycznymi. Przez analogię do ruchu planet wokół Słońca model ten nazwano "modelem planetarnym atomu". Pierwszym równaniem modelu jest równość siły elektrostatycznej i siły dośrodkowej.

Bohr założył, że elektron może krążyć tylko po wybranych orbitach zwanych stabilnymi, oraz że krążąc po tych orbitach nie emituje promieniowania (mimo że tak wynikałoby z rozwiązania klasycznego). Atom wydziela promieniowanie tylko gdy elektron przechodzi między orbitami.

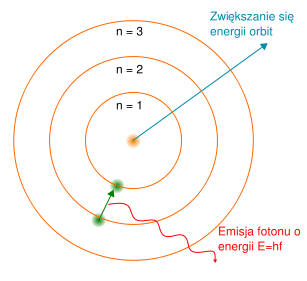
AD 19.

Zjawisko Comptona, rozpraszanie komptonowskie - zjawisko rozpraszania fotonów promieni X, czyli kwantów promieniowania o dużej energii, na swobodnych lub słabo związanych elektronach w wyniku którego promieniowanie elektromagnetyczne zwiększa długość fali (traci energię). Istnieje także jądrowe zjawisko Comptona, ale mówiąc o rozpraszaniu Comptona ma się na myśli rozpraszanie na elektronach.

Zjawisko zachodzi we wszystkich materiałach. Najczęściej z fotonami o średnich energiach: 0,5 do 3,5 MeV, lecz także dla wysoko energetycznych fotonów. Teoretycznie zjawisko zachodzi też dla światła widzialnego lecz zmiana długości fali jest względnie tak niewielka, że trudno ją zaobserwować.

Znaczenie

Jest to jedno z najbardziej znanych doświadczeń dowodzących dualnej natury światła. Z jednej strony traktuje się tu foton jak cząstkę, a zjawisko jak ich zderzenie, ale z drugiej strony jego energię i pęd oblicza się z założeń de Broglie`a. Ponieważ podany wyżej wzór jest potwierdzony przez doświadczenie, świadczy to o słuszności relacji de Broglie`a, a więc i o słuszności dualizmu.

Wykorzystanie

Zjawisko Comptona odgrywa główną rolę w oddziaływaniu promieniowania gamma i rentgenowskiego z materią wywołując pochłanianie go przez substancje.

Zjawisko rozpraszania komptonowskiego gra zasadniczą rolę w radiobiologii, m.in. radioterapii.

Efekt znajduje w zastosowanie w badaniach spektroskopowych przy użyciu promieniowania gamma.

AD 20.

Rentgenowskie promieniowanie, promieniowanie X, rodzaj promieniowania elektromagnetycznego (fale elektromagnetyczne) o długości fali zawartej w przedziale od 0,1 pm do ok. 50 nm, tj. pomiędzy promieniowaniem gamma i ultrafioletowym, przy czym zakres promieniowania rentgenowskiego pokrywa się częściowo z niskoenergetycznym (tzw. miękkim) promieniowaniem gamma - rozróżnienie wynika z mechanizmu wytwarzania promieniowania: promieniowanie rentgenowskie powstaje przy przejściach elektronów na wewnętrzne powłoki elektronowe atomu, natomiast promieniowanie gamma w przemianach energetycznych zachodzących w jądrze atomowym.

Promieniowanie rentgenowskie wykorzystuje się w badaniach strukturalnych (rentgenowska analiza strukturalna, Braggów-Wulfa warunek, lauegram) oraz do badania pierwiastkowego składu chemicznego (rentgenowska analiza widmowa). Ponadto promieniowanie rentgenowskie szeroko stosuje się w diagnostyce medycznej. Promieniowanie rentgenowskie odkrył w 1895 W.C. Roentgen.

AD 21.

Dualizm korpuskularno-falowy - cecha wielu obiektów fizycznych (np: światła czy elektronów) polegająca na tym, że w pewnych sytuacjach, zachowują się one jakby były cząstkami (korpuskułami), a w innych sytuacjach jakby były falami.

Wg mechaniki kwantowej właściwie całą materię charakteryzuje ten dualizm. Każdej cząstce, a nawet każdemu obiektowi makroskopowemu można przypisać charakterystyczną dla niego funkcję falową, wynikającą z probabilistycznej natury materii. Z drugiej strony każde oddziaływanie falowe można opisać w kategoriach cząstek.

Dualizm korpuskularno-falowy jest ściśle zwiazany z falami de Broglie'a. Równanie:

łączy wielkosci falowe (długość fali λ) z korpuskularnymi (pęd p)

AD 22.

Teoria de Broglie

Fale materii, zwane też falami de Broglie'a jest to, alternatywny w stosunku do klasycznego (czyli korpuskularnego), sposób postrzegania obiektów materialnych. Według hipotezy dualizmu korpuskularno-falowego każdy obiekt może być opisywany na dwa sposoby: jako cząstka/obiekt materialny albo jako fala (materii).

Pomysł opisu cząstek za pomocą fal pochodzi od Louisa de Broglie'a, który w 1924 roku uogólnił teorię fotonową efektu fotoelektrycznego. W tym czasie wiedziano już, że na potrzeby opisu niektórych zjawisk fizycznych, z każdą falą elektromagnetyczną można stowarzyszyć pewną cząstkę - foton. Propozycja De Broglie'a polegała na tym, aby każdej cząstce o różnym od zera pędzie przypisać falę, o określonej długości i częstości. Propozycja ta wychodziła naprzeciw wynikom eksperymentalnym, które świadczyły, że w pewnych sytuacjach każda cząstka może zachowywać się jak fala.

Zgodnie z tym, de Broglie zapostulował odwrócenie zależności wyrażającej pęd fotonu stowarzyszonego z falą elektromagnetyczną (zależności znanej z teorii fotonowej), czyli długość fali materii stowarzyszonej z cząstką miała wyrażać się przez pęd cząstki:

gdzie:

• λ - długość fali

• h - stała Plancka

• p - pęd cząstki

Podobnie każdej cząstce o energii E należy przyporządkować inną typową charakterystykę fali, tj. częstotliwość. Wynosi ona f = E / h.

AD 23.

Zasada nieoznaczoności (zasada nieokreśloności) mówi, że niepewność zawsze będzie częścią każdego przewidywania dokonanego przez naukę. Postęp może ją tylko zmniejszać aż do pewnej granicy. Nieoznaczoność nigdy nie będzie równa zeru. Dla niektórych problemów nie da się dokładnie wyliczyć, co się stanie w przyszłości.

Zasada nieoznaczoności mówi, że nie można z dowolną dokładnością wyznaczyć jednocześnie położenia i pędu cząstki

Matematyczna postać zasady:

gdzie:

• Δx - nieokreśloność pomiaru położenia (odchylenie standardowe położenia),

• Δp - nieokreśloność pomiaru pędu (wariancja pędu),

• h - stała Plancka,

• π - pi.

• Ogólna postać zasady [edytuj]

• Jeżeli w danym stanie kwantowym
  wektory
  i
  są prawidłowo określonymi wektorami stanu, to zachodzi:

• 
  

• gdzie:

• σ - odchylenie standardowe
  - dowolne obserwable

---