Imię i nazwisko:	Ćwiczenie nr C6 Wyznaczanie współczynnika napięcia powierzchniowego
Kierunek i rok:	Ocena z kolokwium: ....................................... data ....................... podpis...........................	Ocena ze sprawozdania: ....................................... data ....................... podpis...........................	Ocena końcowa: ....................................... data ....................... podpis...........................
Nazwisko prowadzącego zajęcia:

Siły Van der Waalsa między drobinami cieczy.

Dokładniejszy pogląd na siły Van der Waalsa możemy uzyskać na podstawie dzisiejszej kwantowo-mechanicznej teorii budowy drobin. Drobiny składają się z atomów, te zaś z dodatnich jąder i ujemnych elektronów. Gdy dwie drobiny zbliżają się do siebie, pomiędzy ich elektronami i jądrami działają siły elektryczne przyciągania i odpychania (siły columbowskie), siły magnetyczne pomiędzy momentami magnetycznymi atomów i elektronów i siły elektryczne pomiędzy momentami elektrycznymi drobin. Ponad to pojawiają się specyficzne siły kwantowe (do których należą i siły wiązania chemicznego).

Jeżeli nie występują siły wiązania chemicznego, siły działające pomiędzy drobinami sprowadzają się do przyciągania się nabojów znaku przeciwnego i sił odpychających się miedzy nabojami jednego znaku. W rezultacie siłę F działającą między drobinami można w przybliżeniu uważać za sumę siły przyciągającej i siły odpychającej; te dwie siły są centralne i szybko maleją proporcjonalnie do pewnych potęg odległości (chodzi tu o odległości środków mas drobin). Mamy więc:

Pierwsza składowa odpowiada przyciąganiu, druga - odpychaniu. Zazwyczaj k₁<k₂, a więc siła odpychania szybciej maleje w miarę wzrostu odległości drobin niż siła przyciągania. Wobec tego na większych odległościach drobiny przyciągają się, a przy zbliżeniu się wzajemnym zaczynają się odpychać.

Siłom przyciągania i odpychania odpowiadają energie potencjalne wyrażające się wzorami:

gdzie:

.

Wypadkowa energia potencjalna jest równa:

Przebieg U w zależności od r dla dwu atomów przedstawia wykres (wykonany dla k₂>k₁):

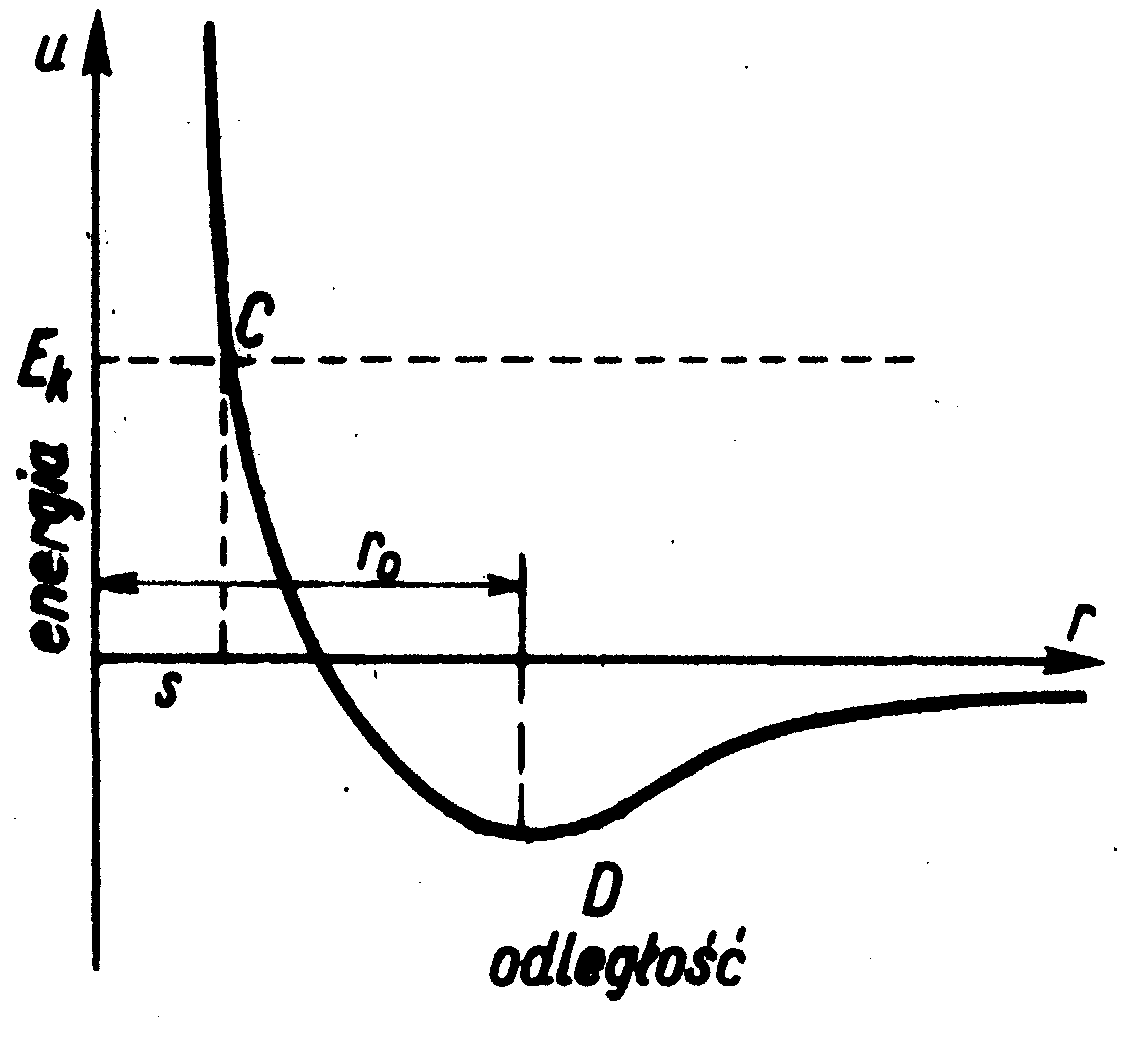
Ma małych odległościach dominują siły odpychania, którym odpowiada stromo wznosząca się część krzywej, na dużych odległościach przeważają siły przyciągania. W punkcie D, który odpowiada odległości r₀ między atomami, siły działające między tymi atomami znoszą się nawzajem. Mamy tu minimum energii potencjalnej, a więc położenie równowagi.

Przypuśćmy teraz, że do atomu A, który jest nieruchomy, zbliża się z dużej odległości drugi atom B. W dużych odległościach od A energia potencjalna B jest praktycznie równa 0, atom B ma więc tylko energię kinetyczną. Jego całkowita energia jest równa U = E_k. Energię tą przedstawia prosta przerywana na powyższym wykresie. W miarę zbliżania się do A atom B uzyskuje dodatkową dalszą energię kinetyczną kosztem energii potencjalnej; całkowitej energii kinetycznej B odpowiada odległość poziomej przerywanej linii od krzywej energii potencjalnej. Jak widzimy, na odległości równowagi r₀ od A atom B ma dużą energię kinetyczną, a siły Van der Waalsa nie wystarczają do powiązania A i B w drobinę; byłoby to możliwe przy jednoczesnym zbliżeniu się trzeciego atomu, który mógłby zabrać niepotrzebną energię kinetyczną. Zbliżając się jeszcze bardziej do A atom B zaczyna tracić energię kinetyczną, która przetwarza się w potencjalną. W punkcie C energia kinetyczna atomu staje się równa zeru; odległość obu atomów wynosi dla tego punktu s. W punkcie tym atom B traci całą swą prędkość i następnie zawraca. Wartość s określa najmniejszą odległość, na jaką mogą zbliżyć się do siebie środki atomów A i B. Jest to efektywna średnica atomu, jeśli atomy A i B są jednakowe, lub suma promieni atomów A i B, gdy są to atomy różne; analogicznie przedstawia się sytuacja, gdy A i B są drobinami. Ściśle biorąc dla każdej energii mamy inna wartość s.

Mechanika kwantowa pozwala w przybliżeniu obliczyć omówione tu siły między atomowe, bądź też analogicznie siły międzydrobinowe, czyli tzw. siły Van der Waalsa. Prócz tego miedzy atomami mogą działać inne siły, tzw. siły wiązania chemicznego.

Siły Van der Waalsa między drobinami czy atomami jednego rodzaju nazywać będziemy siłami spójności. Siły te maleją szybko wraz ze wzrostem odległości i dlatego też można mówić o określonej sferze działania tych sił. Chodzi tu o obswzar, w którym te siły wywierają dostrzegalne działanie.

Weźmy pod uwagę drobinę, która znajduje się we wnętrzu cieczy i zakreślimy dookoła niej kulę o promieniu równym promieniowi sfery działania. Jedynie te drobiny, których środki znajdują się we wnętrzu lub na powierzchni tej kuli, wywierać będą na nasza drobinę działanie. Przedstawia to rysunek:

Średnio biorąc, drobiny rozłożone są równomiernie w cieczy, a wobec tego wypadkowa sił wywieranych na drobinę przez otaczające ją drobiny równa będzie w przybliżeniu zero. Oczywiście zachodzić mogą i będą fluktuacje gęstości drobin i wskutek tego będą występować niewielkie siły wypadkowe, powodujące nieregularne - brownowskie - ruchy naszej drobiny, w ciągu jednak dłuższych odstępów czasu średnia wartość siły wypadkowej działającej na drobinę we wnętrzu cieczy równa jest zeru.

Inaczej zupełnie wygląda sytuacja drobiny znajdującej się na powierzchni cieczy, bądź też w pobliżu jej powierzchni. Gdy drobina jest na powierzchni cieczy, jedynie w dolnej połowie jej sfery działania znajdują się inne drobiny cieczy; w górnej natomiast mamy nieliczne tylko drobiny powietrza i pary nasyconej nad cieczą. Sytuację tą przedstawia rysunek:

Wobec tego wypadkowa sił wywieranych na naszą drobinę przez inne drobiny cieczy, czyli wypadkowa siła spójności, skierowana jest pionowo ku dołowi. Wypadkowa sił pochodzących od drobin w górnej połowie sfery działania będzie skierowana ku górze, lecz jest ona kilkaset razy mniejsza i ulega o wiele silniejszym fluktuacjom. Tą ostatnia wypadkową można zaniedbać wobec wypadkowej skierowanej ku dołowi. Tak więc drobiny cieczy znajdujące się na jej powierzchni poddane są stale działaniu sił wywieranych przez inne drobiny cieczy. Oznacza to, że we wnętrzu cieczy panuje ciśnienie wewnętrzne, równe stosunkowi wspomnianej wyżej siły do swobodnej powierzchni cieczy. Ciśnie to nie jest więc niczym innym, jak odpowiednikiem dodatkowego ciśnienia:

wprowadzonego przez Van der Waalsa do równania gazów rzeczywistych. Z równania Van der Waalsa obliczyć można wartość tego ciśnienia:

dla wody np. wynosi ono około 17 000 atmosfer.

Napięcie powierzchniowe.

Napięcie powierzchniowe warstwy cieczy nie zależy od wielkości powierzchni, lecz tylko od rodzaju cieczy i od jej temperatury. Liczbowo napięcie powierzchniowe jest równe sile działającej stycznie do powierzchni cieczy na jednostkę długości obrzeżenia powierzchni cieczy. Napięcie powierzchniowe wyrażamy zwykle w dynach/cm lub ergach/cm².

Jedna z metod oznaczania napięcia powierzchniowego, tzw. metoda stalagmometryczna, oparta jest na mierzeniu wielkości kropli odrywającej się od rurki o określonej średnicy. Kropla nie jest kulą, lecz pewną powierzchnią obrotową. Na chwilę przed oderwaniem się ciężar kropli utrzymany jest przez napięcie powierzchniowe.

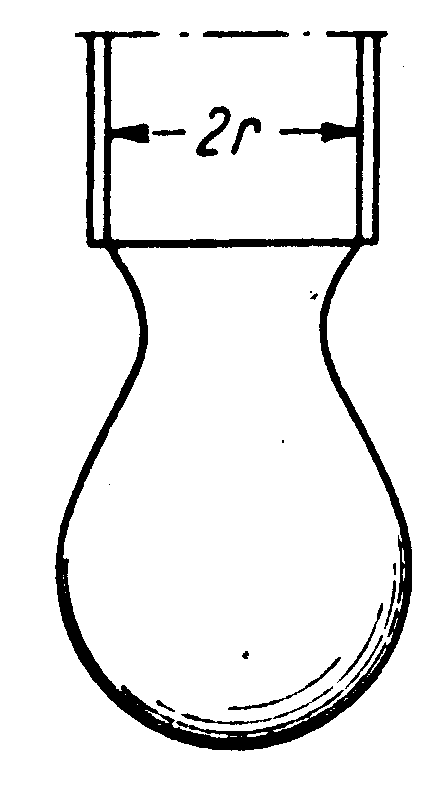
Gdy nie było przewężenie widocznego na rysunku i gdyby kropla odrywała się wzdłuż płaszczyzny ograniczającej rurkę, mielibyśmy jako warunek równowagi:

m - masa kropli,

r - promień rurki.

Ze względu na przewężenie kropli wprowadzić należy odpowiedni czynnik poprawkowy f; dokładniejsze badania wykazują, że czynnik ten jest określoną funkcją r/V^1/3, której wartości podane są w tablicach. Ostatecznie więc:

V - objętość kropli.

Gdy policzymy liczbę kropli odrywających się od rurki, to ze znanej objętości cieczy, mając daną gęstość tej cieczy, możemy łatwo obliczyć objętość i masę jednej kropli, a z powyższego wzoru znajdziemy następnie σ. Dla mniej dokładnych pomiarów możemy zastąpić funkcję f przez stałą i wówczas dla dwu różnych cieczy mamy w przybliżeniu:

W ten sposób możemy szybko porównać ze sobą napięcia powierzchniowe cieczy znając ich gęstości i określając liczbę kropli potrzebną do wypływu określonej objętości cieczy.

Napięcie powierzchniowe wiąże się bezpośrednio z pracą wbrew siłą spójności, potrzebną do zwiększania swobodnej powierzchni cieczy na jednostkę. Praca ta wyraża się w ergach/cm².

Praca zużyta na zwiększenie powierzchni cieczy zmagazynowana zostaje w postaci energii powierzchniowej cieczy. Energia ta może zostać zmieniona z powrotem na pracę, gdy powierzchnia swobodna cieczy maleje. Zarówno zwiększanie, jak i zmniejszanie powierzchni cieczy odbywa się zwykle izotermicznie; termodynamika prowadzi nas zatem do wniosku, że energię powierzchniową cieczy uważać należy za energię swobodną F. Ponieważ:

Znajdujemy zgodnie z równaniem Helmholtza-Gibbsa:

Ale w naszym przypadku mamy:

a - wielkość powierzchni cieczy.

u - energia wewnętrzna na jednostkę powierzchni cieczy.

Ostatecznie otrzymujemy:

Doświadczenie wykazuje, że w miarę wzrostu temperatury napięcie powierzchniowe maleje i staje się równe zeru w temperaturze krytycznej. Zjawisko to ilustruje wykres:

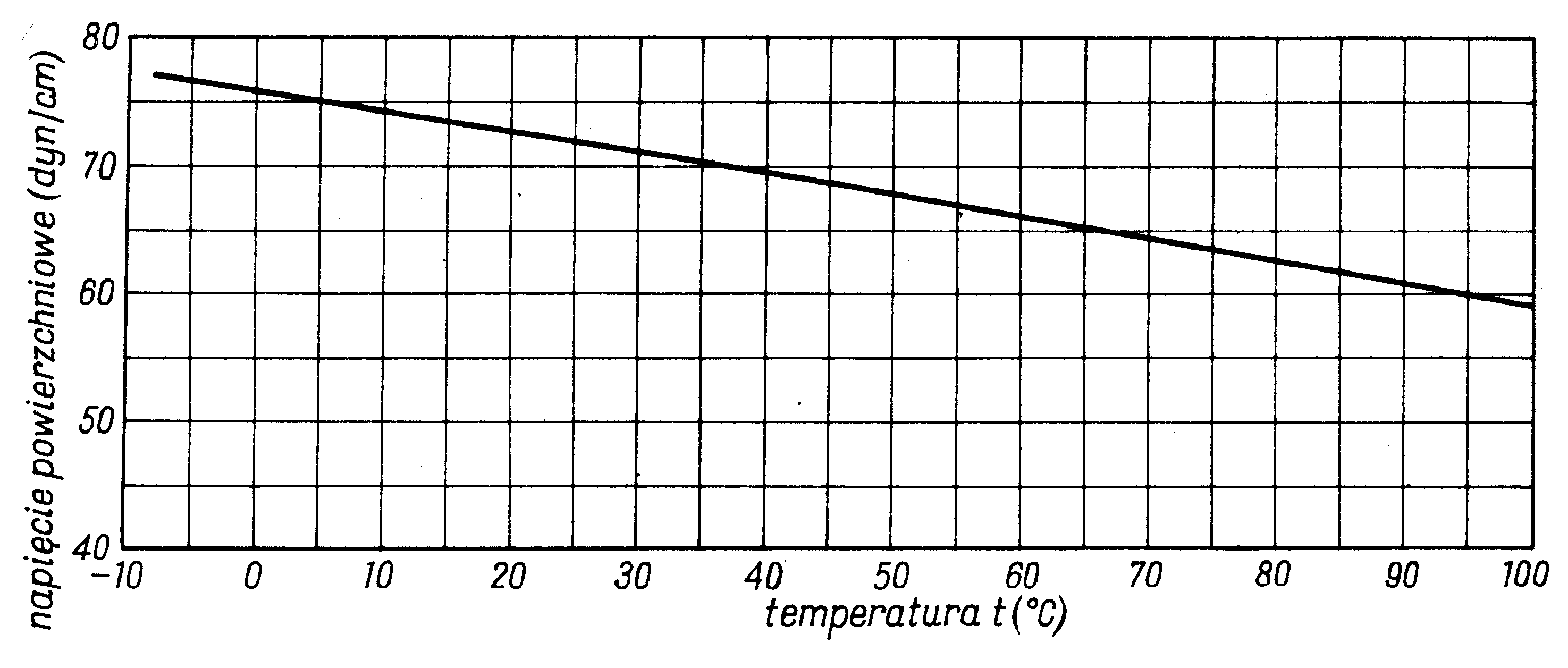
W temperaturze tej zanika różnica pomiędzy cieczą a parą nasycona, znikać więc musi menisk cieczy i napięcie powierzchniowe. Wobec tego (dσ/dT)<0; z powyższego wzoru wynika, że u>σ, w warunkach izotermicznych musi więc zachodzić przy zwiększaniu powierzchni cieczy dopływ ciepła z otoczenia.

Wartość napięcia powierzchniowego cieczy jest bardzo zależna od zanieczyszczenia.

Przyleganie i kąty zetknięcia.

Jeżeli chodzi o siły molekularne, działające pomiędzy drobinami cieczy, a jakiegoś ciała stałego, to tego rodzaju siły prowadzą do zjawisk przylegania. Siły przylegania występują w praktyce bardzo często.

Za miarę przylegania P cieczy do ciała stałego możemy przyjąć pracę potrzebną do oderwania cieczy od ciała stałego na powierzchni 1 cm².

Powierzchnia zetknięcia się ciała stałego z cieczą jest również siedziba pewnej energii powierzchniowej, podobnie jak swobodna powierzchnia cieczy. W związku z tym możemy mówić o napięciu powierzchniowym ciał stałych w zetknięciu z cieczą, gazem lub innym ciałem stałym. Jednakże pomiar napięć powierzchniowych ciał stałych jest bardzo trudny do przeprowadzenia, tak że potrafimy tylko uporządkować napięcia ciał stałych według ich wielkości, ale nie znamy samych wielkości.

Ściśle biorąc, napięcie powierzchniowe zależy zatem od dwu ciał stykających się ze sobą. Jeśli fazę gazową będziemy oznaczać wskaźnikiem 1, ciekłą - wskaźnikiem 2, stałą - wskaźnikiem 3, to napięcie powierzchniowe cieczy w zetknięciu z gazem oznaczać należy przez σ₁₂, ciała stałego z gazem σ₁₃ i wreszcie ciała stałego w zetknięciu z cieczą przez σ₂₃. jeśli powierzchnia zetknięcia się cieczy ze ścianką wzrośnie o jednostkę kosztem swobodnej powierzchni ścianki, wymaga to pracy:

Jeśli oderwiemy ciecz od ścianki na powierzchni 1 cm², wówczas powierzchnie swobodne cieczy i ścianki wzrosną każda o 1 cm², powierzchnia zaś zetknięcia się cieczy ze ścianką zmaleje o 1 cm², wobec tego przyrost energii powierzchniowej, równy włożonej pracy, jest:

przez σ oznaczyliśmy σ₁₂.

Pamiętając o definicji przylegania mamy:

Możemy rozróżnić teraz trzy przypadki:

1. P = 0, co oznacza, że ciecz nie przylega w ogóle do ścianki. Mamy wtedy:

2. P < σ, a zatem σ - σ' > σ, skąd σ' > 0, czyli:

W tym przypadku jest energetycznie korzystne zmniejszyć powierzchnie styku cieczy z ciałem stałym, a zwiększyć powierzchnię swobodna ciała stałego. W ten sposób zachowuje się kropla rtęci na szkle. Taka ciecz nazywamy niezwilżającą.

3. P > σ, a zatem σ - σ' > σ, skąd σ' < 0, czyli:

W tym przypadku energetycznie korzystne jest powiększenie powierzchni styku cieczy z ciałem stałym, a zmniejszenie powierzchni swobodnej ciała stałego. Ciecz usiłuje przylgnąć na możliwie dużej powierzchni do ciała stałego, rozlewa się po nim, jak np. nafta po szkle. Powiadamy, że ciecz zwilża ciało stałe i dlatego ciecz taką nazywamy zwilżającą.

Wartość przylegania decyduje o kształcie powierzchni cieczy w pobliżu ścianki naczynia. W dużym naczyniu z dala od ścianek powierzchnia cieczy (menisk cieczy) jest płaska, jednak w pobliżu ścianek łatwo jest zauważyć, że menisk cieczy staje się zakrzywiony.

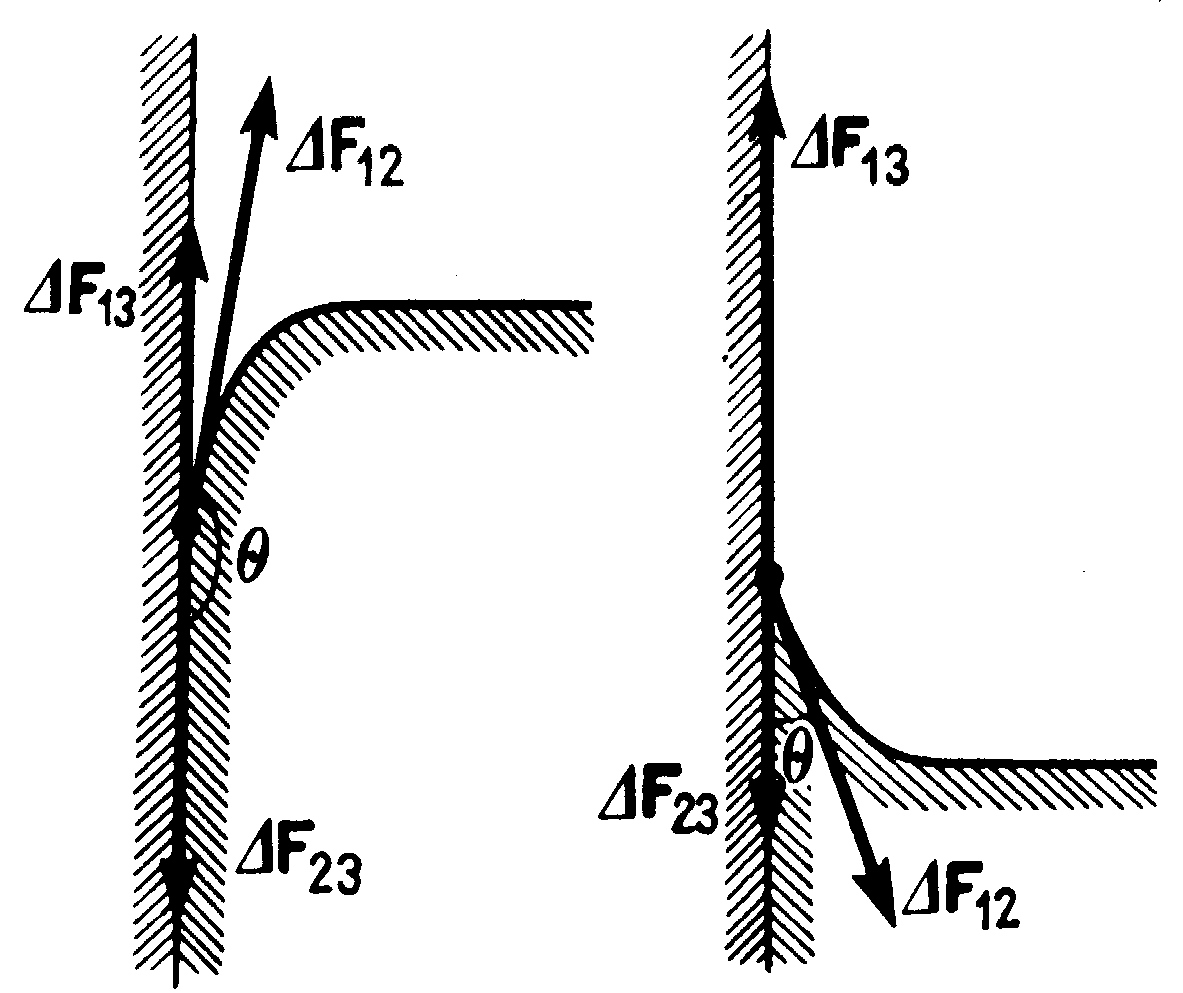
Na poniższym rysunku przedstawiono menisk rtęci przy szklanej ściance (a) oraz menisk wody przy szklanej ściance (b):

a) b)

Kąt Θ, pod którym powierzchnia cieczy przecina ściankę, ma zupełnie określona wartość, zależną od stosunku spójności cieczy do jej przylegania do ścianki.

Zjawisko włoskowatości.

Napięcie powierzchniowe cieczy i przyleganie cieczy do ścianek powoduje występowanie tzw. zjawisk włoskowatości, pozornie sprzecznych ze zwykłymi prawami hydrostatyki. Zjawiska te występują najwyraźniej w wąskich rurkach, tzw. rurkach włoskowatych, skąd też pochodzi ich nazwa.

Zjawiska włoskowatości wyglądają inaczej wtedy, gdy ciecz zwilża ściankę rurki, niż wtedy, gdy ciecz jest niezwilżająca.

Jeżeli do naczynia z wodą zanurzymy rurkę szklaną otwartą do góry i u dołu, zauważymy, że woda w rurce podnosi się do pewnej wysokości tworząc menisk wklęsły.

Odgrywa tu przede wszystkim rolę, kąt Θ styku powierzchni wody ze szkłem. Dla wody kąt ten jest ostry i bliski zeru, znaczy to, że powierzchnia wody u ścianki zakrzywia się ku górze, tak że powstaje menisk wklęsły. Ale pod powierzchnią niż takiego menisku, stanowiącego w wąskiej rurce część powierzchni kuli, ciśnienie jest znacznie mniejsze niż pod płaską powierzchnią cieczy i to o wartość:

R - promień krzywizny powierzchni cieczy.

Ten niedobór ciśnienia w porównaniu z ciśnieniem na zewnątrz rurki, gdzie promień krzywizny powierzchni cieczy nawet w sąsiedztwie ścianki jest dużo większy, a praktycznie jest nieskończenie wielki w większych odległościach od ścianki, powoduje wypychanie cieczy w rurce ku górze na taką wysokość, by ciśnienie hydrostatyczne słupa cieczy równoważyło niedobór ciśnienia. A więc ciecz zwilżająca wznosi się w rurce włoskowatej ku górze.

Obliczymy teraz wysokość, na jaką wzniesie się ciecz ku górze.

R - oznacza promień rurki, Θ - kąt styku powierzchni cieczy ze ścianką, R₁ - promień krzywizny menisku.

Otrzymujemy:

Kąt miedzy R₁, promieniem rurki jest równy kątowi Θ, gdyż oba te kąty mają ramiona do siebie prostopadłe. Wobec tego niedobór ciśnienia jest równy:

Z drugiej strony, jeśli ciecz w rurce wzniesie się o h nad poziom cieczy w naczyniu, a jej gęstość jest ρ, ciśnienie hydrostatyczne tego słupka na poziom cieczy w naczyniu jest równy:

g - przyspieszenie ziemskie.

Ponieważ ciśnienie to jest równoważone przez napięciowy niedobór ciśnienia, otrzymujemy:

skąd:

Dla wody Θ ≈ 0, a więc:

Jak widzimy napięcie powierzchniowe jest proporcjonalne do wysokości wzniesienia się cieczy w rurce.

Dla cieczy niezwilżających menisk jest wypukły, a kąt Θ jest większy od π/2.

W tym przypadku pod meniskiem mamy nadwyżkę ciśnienia równą:

która wciska ciecz w rurce poniżej poziomu w naczyniu na taka głębokość h, by ciśnienie hydrostatyczne cieczy otaczającej rurkę równoważyło nadwyżkę napięciową ciśnienia.

Jeżeli Θ' = π - Θ, to:

warunek równowagi daje nam:

skąd:

wzory te można wyprowadzić również inaczej pisząc, że ciężar cieczy w rurce nad (czy też pod) poziomem cieczy w naczyniu równoważony jest przez siły napięcia powierzchniowego działającego na ścianki rurki. Napięcie to jest równe co do wartości bezwzględnej σ'. Mamy więc:

Ponieważ zaś:

znajdujemy ostatecznie:

Wzór jest identyczny z otrzymanym poprzednio wzorem.

Tabela wyników pomiarów:

Lp.	h [m]	hśr [m]	r [m]	ρ [kg/m^3]	σ [N/m]	σśr [N/m]
1	0,020	0,0192	70·10^-5	0,99729	6,84839·10^-5	6,57445·10^-5
2	0,018								6,16355·10^-5
3	0,018								6,16355·10^-5
4	0,018								6,16355·10^-5
5	0,020								6,84839·10^-5
6	0,020								6,84839·10^-5
7	0,020								6,84839·10^-5
8	0,020								6,84839·10^-5
9	0,018								6,16355·10^-5
10	0,020								6,84839·10^-5

∆h = ± 0,0005 m

∆r = ± 5·10^-5 m

g = 9,81 m/s²

Z tablic odczytuje gęstość wody w temperaturze t =13,6 ºC = 296,75 K:

ρ = 0,99729 kg/m³

Wyznaczam napięcie powierzchniowe:

σ = 6,574454813·10^-5 N/m

Wyznaczam niepewność pomiaru metodą różniczki zupełnej:

∆ σ = ± 0,640813676·10^-5 N/m

Wyznaczam niepewność procentową pomiaru:

Np = ± 9,747%

WNIOSKI:

Na wartość napięcia powierzchniowego mają wielki wpływ obce ciecze lub rozpuszczone ciała stałe. W związku z tym koniecznym i zasadniczym warunkiem uzyskania poprawnych wyników jest jak najdalej posunięta czystość rurki kapilarnej oraz naczynia z cieczą. Największym błędem w tych pomiarach jest wielkość h, występujący tu błąd ∆h wyznaczam na podstawie 10 kolejnych pomiarów - jako błąd średni kwadratowy. Błąd promienia rurki ∆r również ma wpływ na otrzymane przeze mnie wyniki.

---