Jóżwiak Andrzej

Myk Robert 10 październik 2001

Specjalność - wiertnictwo

Rok III grupa V

Temat: Pomiar stałej dielektrycznej skał.

Jedną z własności fizycznych wykorzystywanych do analizy próbek skał jest stała dielektryczna ε . Jest to miara podatności próbki na polaryzację zewnętrznym polem elektrycznym kształtującym wewnętrzną strukturę elektryczną w postaci dipoli. Przesunięcia ładunków powodują indukowanie się na przeciwległych powierzchniach próbki ładunków

o przeciwnego znaku o potencjale
.

E_w- średnie przestrzenne natężenie pola elektr. wewnątrz próbki.

l- uśredniona odległość ładunków powierzchniowych.

W praktyce pomiary stałej dielektrycznej prowadzi się przy założeniu niezmienności napięcia między ładunkami powierzchniowymi spolaryzowanej próbki. Dokonuje się tego za pomocą kondensatora zawierającego między okładkami badaną próbkę, którego elektrody zasilane są ze źródła napięcia. W przypadku tym natężenie wewnętrznego pola elektr. próbki jest niezależne od rodzaju wypełniającego kondensator dielektryka. Zewnętrzne natężenie pola zwanego indukcją elektryczną lub przesunięciem elektr. powinno wynosić

D = ε⋅ E_w

Lub powinno być większe o przyrost natężenia pola pochodzącego od ładunków polaryzacji powierzchniowej P.

D = E_w + 4⋅π⋅P

Polaryzacja P ilościowo jest równa ilorazowi ładunku powierz. Q_p do powierzchni S.

1. Pomiar stałej dielektrycznej próbki skalnej z wielkości powierz. ładunku polaryzacji kondensatora

Pojemność pustego kondensatora wynosi

- Q₀ ładunek powierzchniowy pustego kondensatora

- U napięcie między okładkami kondensatora

Wprowadzenie między okładki badanej próbki skalnej powoduje powstanie powierzchniowego ładunku polaryzacji, który ulega zneutralizowaniu dzięki przepływowi ładunku zwanego związanym w obwodzie zewnętrznym kondensatora . Pojemność kondensatora z dielektrykiem jest powiększona wskutek przyrostu ładunku o wartość ∆C.

lub

C_D = є · C₀

Ilościowo omawiane zjawisko wskazuje ile razy wzrasta pojemność kondensatora jeśli zamiast próżni między jego okładkami znajduje się dielektryk (badana próbka skalna).

Z tego wynika że

Zależność ta służy do realizacji pomiarów stałej dielektrycznej. Do określenia pojemności początkowej konieczna jest znajomość powierzchni okładzin kondensatora , wzajemnej odległości między elektrodami i wartości bezwzględnej przenikalności powietrza.

gdzie:

- C₀ pojemność początkowa

• є_p przenikalność powietrza

• S powierzchnia okładzin

• l odległość między elektrodami

Ostateczny wzór pozwalający określić stałą dielektryczną skały z przyrostu pojemności kondensatora pomiarowego ma postać:

gdzie:

• є stała dielektryczna badanej próbki skalnej

• ∆C różnica pojemności kondensatora pomiarowego zawierającego między okładkami badaną próbkę i pojemności kondensatora pustego , ∆C = C_D-C₀ [pF]

• l odległość między elektrodami [cm]

• S powierzchnia próbki, na której indukuje się ładunek polaryzacji [cm²]

Wyznaczana stała dielektryczna skał charakteryzuje ich własności elektryczne

i elektromagnetyczne, które zależą między innymi od:

• składu chemicznego oraz mineralnego skały

• składu nasycających je faz ciekłych i gazowych oraz stosunku tych faz w jednostce objętości

• częstotliwości pola polaryzującego

• temperatury próbki

• kształtu i orientacji cząstek dielektrycznych

• gęstości

Dielektryczna przenikalność skał osadowych zmienia się od 2,5 do 40. Anhydryt, gips, sól kamienna i inne skały pochodzenia chemicznego słabo różnią się między sobą elektryczną przenikalnością, która wynosi zwykle około 6. Stała dielektryczna piasków, piaskowców, glin, wapieni i dolomitów zależy przede wszystkim od ich porowatości i wilgotności, w mniejszym stopniu od mineralogicznego składu fazy stałej.

Wynika to stąd że przenikalność dielektryczna wody jest znacznie wyższa i wynosi 68 przy temperaturze 0˚C do 55 przy 100˚C. Przenikalność dielektr. skały maleje w przypadku gdy płynną fazą nasycającą skałę jest nafta(є= 2,5).

Zmiany własności elektrycznych wraz z częstotliwością pola polaryzującego są związane z bezwładnością procesów polaryzacji. Spolaryzowane dipole powyżej pewnej częstotliwości nie nadążają za jego zmianami, co prowadzi do zmniejszenia є, ponieważ nie osiąga swej ostatecznej wielkości.

Ze wzrostem temperatury przenikalność elektryczna ciał stałych z powodu osłabienia sprężystych wiązań między atomami, elektronami i jonami nieznacznie wzrasta, natomiast dla wody maleje.

2. Obliczenia stałej dielektrycznej poszczególnych próbek.

• próbka o symbolu 30A

przy częstotliwości F=10 [kHz]

= 1+11,298
= 17,907 [pF/cm]

gdzie S=л∙

D - średnica próbki (6,55 cm)

l - grubość próbki (1,22 cm)

∆ є=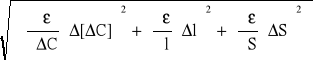

∆l, ∆D =0,005 [cm]

∆[∆C]= 2 [pF]

∆S=
=0,05 [cm²]

∆ є= 0,8484 =0,8

є = 17,9
[pF/cm]

- dla F = 1 [MHz]

є = 8,18579

∆ є = 0,8459

є = 8,2
[pF/cm]

• dla F = 10 [MHz]

є = 6,49501

∆ є = 0,8457

є = 6,5
[pF/cm]

próbka o symbolu 2

S=л∙
= 27,141[cm²]

dla F= 10 [kH]

= 1+11,298
= 8,9091 [pF/cm]

D - średnica próbki (5,83 cm)

l - grubość próbki (0,98cm)

∆ є=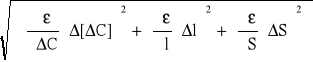

∆l, ∆D =0,005 [cm]

∆[∆C]= 2 [pF]

∆S=
=0,05 [cm²]

∆ є= 0,79214 = 0,8

є = 8,9
[pF/cm]

dla F = 1 [MHz]

є = 6,1409

∆ є =0,7914 = 0,8

є = 6,1
[pF/cm]

dla F = 10 [MHz]

є = 5,3500

∆ є =0,79128 = 0,8

є = 5,4
[pF/cm]

Zestawienie wyników:

częstotliwość		10 [kH]	100 [kHz]	1 [MHz]	10 [MHz]
Є [pF/cm]	Próbka 30A	17,9		8,2	6,5
		Próbka nr 2	8,9		6,1		5,4

Wnioski:

W przeprowadzonym ćwiczeniu dokonywaliśmy pomiaru stałej dielektrycznej skał za pomocą E- metru .Pomiar sprowadzał się do określenia pojemności kondensatora pustego a następnie pojemności kondensatora z badaną próbką. Znając zmianę pojemności oraz wymiary próbki skalnej ze wzoru określiliśmy stałą dielektryczną. Z uzyskanych wyników możemy wnioskować o zależności między stałą dielektryczną a częstotliwością pola polaryzującego. Im większa częstotliwość tym mniejsza stała dielektryczna próbki.

E_W

P

+++++++++++

___________

l

U=E_w·l

-P

gęstość łądunków

polaryzacji na

powierzchni próbki

gęstość ładunków

na okładce

---