1. Cel ćwiczenia:

Głównym zadaniem jest doświadczalne i teoretyczne wyznaczenie kształtu swobodnej powierzchni cieczy w naczyniu cylindrycznym, które wiruje wokół pionowej osi.

2. Schemat stanowiska pomiarowego:

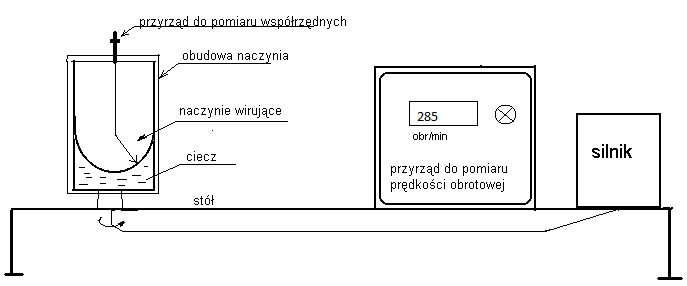
3. Tabela pomiarowa

Obr/min	198	Obr/min	243	Obr/min	285
x [mm]	z [mm]	x [mm]	z [mm]	x [mm]	z [mm]
3,4	141,04	4,21	151,88	21,33	150,14
16,83	137,06	14,92	148,13	23,48	146,03
22,67	133,03	19,63	144	25,73	141,99
26,75	129,11	22,76	140	27,89	138,06
30,91	125,04	25,35	136,4	29,44	134,12
33,38	121	27,48	132,25	30,87	130,11
36,21	117,06	30,07	128,14	32,39	126,03
38,86	113,13	32,32	124,37	33,45	122
41,01	109,1	34,02	120,04	35,05	117,99
43,35	105,12	36,48	116,01	35,8	114,03

4. Wzory oraz przykładowe obliczenia

Prędkość kątowa:

v- zadana prędkość, T- okres drgań, g- przyspieszenie ziemskie.

Wysokość paraboloidy:

R=D/2=45 [mm] - promień naczynia

h₂=141,04 [mm]

h₁=105,12 [mm]

H= h₂ - h₁= 35,92 [mm] - wysokość cieczy

Prędkości kątowe wynoszą odpowiednio:

5. Wnioski

Podczas ruchu obrotowego wokół osi pionowej naczynia z płynem, powierzchnia swobodna cieczy przybiera kształt paraboloidy obrotowej. Jej odwzorowaniem na wykresie jest parabola, której płaszczyzna przekroju jest prostopadła do osi symetrii tejże paraboloidy, a jej oś pokrywa się z osią obrotu naczynia.

Wraz ze wzrostem prędkości kątowej ϖ, ramiona paraboloidy obrotowej w płaszczyźnie przekroju zaczynają się wprost proporcjonalnie wydłużać, jej wierzchołek obniża się, natomiast powierzchnia o największym przekroju kołowym stale się podnosi.

Wyniki przeprowadzonych pomiarów są zbieżne z obliczeniami teoretycznymi.

---