RACHUNEK CAŁKOWY

CAŁKI NIEOZNACZONE

1. F(x) nazywamy funkcja pierwotną funkcji f(x) na przedziale X wtedy i tylko wtedy gdy
   

2. Podstawowe twierdzenie o funkcjach pierwotnych: Jeżeli funkcja F(x) jest funkcją pierwotną funkcji f(x) w przedziale X to również funkcją pierwotną f(x) jest funkcja F(x)+C, gdzie C jest dowolną stałą. Każdą funkcję pierwotną G(x) funkcji f(x) w przedziale X można przedstawić w postaci F(x)+C
   , gdzie
   jest odpowiednią stałą.

3. Definicja : Całką nieoznaczoną funkcji f(x) nazywamy rodzinę jej funkcji pierwotnych:

4) TW ( o istnieniu funkcji pierwotnej): Jeżeli funkcja f jest ciągła na przedziale X, to ma na tym przedziale funkcję pierwotną

5) TW: Jeżeli f(x) i g(x) są całkowalne (posiadają rodzinę funkcji pierwotnych) to również całkowalne są funkcje f(x)+g(x), f(x)-g(x) i kf(x), gdzie k jest dowolna stałą i prawdziwe są wzory

6) TW o całkowaniu przez podstawianie: Jeżeli funkcja g(x) ma ciągłą pochodną w przedziale a funkcja f(x) jest ciągła w zbiorze wartości funkcji g to prawdziwy jest wzór nazywany wzorem na całkowanie przez podstawianie
t=g(x)

7) różniczka funkcji jest to iloczyn pochodnej funkcji i przyrostu jej argumentu (
)

8. TW o całkowaniu przez części : Jeżeli funkcje f i g mają na pewnym przedziale ciągłe pochodne to na tym przedziale prawdziwy jest wzór
   

CAŁKA OZNACZONA RIEMANNA

Ciąg podziałów przedziału <a,b> nazywamy ciągiem normalnym podziałów wtedy i tylko wtedy, gdy odpowiadający mu ciąg średnic dąży (jest zbieżny) do zera.

Definicja całki oznaczonej Riemanna

Jeżeli dla dowolnego ciągu normalnego podziałów przedziału <a,b> odpowiadający mu ciąg sum całkowych Riemanna dąży do tej samej granicy niezależnie od sposobu wyboru punktów ξ_i to tę granicę nazywamy całką oznaczoną Riemanna funkcji f na przedziale <a,b>

a - dolna granica całkowania

b - górna granica całkowania

Interpretacja geometryczna

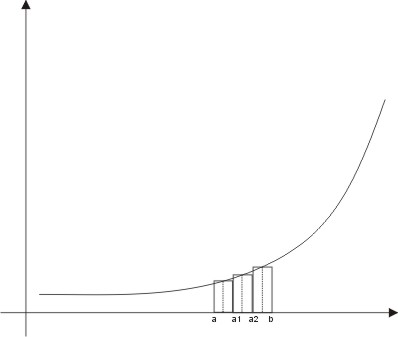
Suma całkowa Riemanna to suma pól tak powstałych prostokątów.

Suma całkowa Riemanna przybliża nam pole obszaru ograniczonego wykresem f(x), prostymi x=a, x=b oraz osią odciętych.

Własności całki oznaczonej:

1.

2. f i g całkowalne w <a,b>
również całkowalne są funkcje f(x)
g(x) , k f(x) i prawdziwe są wzory:

3. f całkowalna w <a,b> i c należy do <a,b>

4. f całkowalna w <a,b> i

5. f i g całkowalne w <a,b> i

6. funkcja całkowalna w <a,b> i

7. twierdzenie o wartości średniej dla całki oznaczonej:

f ciągła w <a,b>

{z każdego kształtu da się zrobić prostokąt}

8. twierdzenie o całkowaniu przez części :

f, g mają ciągłą pochodna w <a,b>

gdzie

9. twierdzenie o całkowaniu przez podstawianie

g(x) posiada ciągłą pochodna w <a,b> i przekształca ten przedział na zbiór, na którym określona jest ciągła funkcja f(t)

,

10. twierdzenie Newtona - Leibniza

Jeżeli F(x) jest jakąkolwiek funkcją pierwotną ciągłej funkcji f(x)to:

-

Całki niewłaściwe 1 rodzaju

f(x) całkowalna w sensie Riemanna w przedziale <a,T> dla dowolnego T>a

Wtedy:

Całką niewłaściwą 1 rodzaju definiujemy jako granicę przy
z całki :

Jeżeli ta granica istnieje i jest właściwa to całkę nazywamy zbieżną. W przeciwnym wypadku całkę nazywamy rozbieżną.

f(x) całkowalna w sensie Riemanna w przedziale <T,b> dla dowolnego T<b

Wtedy:

Całką niewłaściwą 1 rodzaju definiujemy jako granicę przy
z całki :

Jeżeli ta granica istnieje i jest właściwa to całkę nazywamy zbieżną. W przeciwnym wypadku całkę nazywamy rozbieżną.

c - dowolna liczba rzeczywista

Zbieżność:

Całka jest zbieżna wtedy i tylko wtedy, gdy te dwie całki są zbieżne. W przeciwnym wypadku będzie rozbieżna.

Całki niewłaściwe 2 rodzaju

1. Funkcja f(x) nie jest określona w punkcie a, ale jest całkowalna w sensie Riemanna w przedziale <a+
,b> , 0<
<b-a . Całkę niewłaściwą 2 rodzaju definiujemy jako:

Granica istnieje, zbieżna
całka zbieżna

2. Funkcja f(x) nie jest określona w punkcie b, ale jest całkowalna w sensie Riemanna w przedziale <a, b-
> , 0<
<b-a . Całkę niewłaściwą 2 rodzaju definiujemy jako:

Granica istnieje, zbieżna
całka zbieżna

3.Funkcja nie jest określona w punkcie c, c

zbieżność, gdy obie zbieżne

SPRAWDZAĆ CZY RIEMANNA CZY NIEWŁAŚCIWA!!!!

Ekonomia:

1. tam gdzie sumowanie w sposób ciągły, a nie w momentach, tam całkowanie (np. strumienie wydatków)

2. pomiędzy przyrostem kapitały a inwestycjami ścisły związek: K'(t)=I(t), strumień czasowy <a,b>
   

4

---