Wykonanie ćwiczenia:

szybkość reakcji v = k(a-x) (x stężenie substratu)

Zadanie 1. Obliczyć czas potrzebny do zmniejszenia stężenia substratu:

1. z 0,25 M do 0,05 M przy stałej szybkości reakcji k = 0,027 min^-1.

t - czas reakcji ?

k = stała szybkość reakcji 0,027 min^-1

a - stężenie początkowe 0,25 M

(a-x) - stężenie końcowe w danym momencie 0,05 M

zamieniamy k na t miejscami

2. z 0,4 M do 0,15 M przy stałej szybkości reakcji k = 0,322 s^-1

t - czas reakcji ?

k = stała szybkość reakcji 0,322 s^-1

a - stężenie początkowe 0,4 M

(a-x) - stężenie końcowe w danym momencie 0,15 M

1. z 0,1 M do 0,02 M przy stałej szybkości reakcji k = 0,108 l/min.

Zadanie 2.

1. Obliczyć energię aktywacji, przyjmując, że podczas hydrolizy w temp. 25^oC szybkość V_m reakcji wynosiła 0,27 mg/min, a w temp. 35^oC 0,48 mg/min.

2. Wyliczyć energię aktywacji, wiedząc, że stała szybkości reakcji w temp. 27^oC wynosiła 0,245.

3. Energia aktywacji pewnej reakcji wynosi 50 kJ/mol. Jak zmieni się stała szybkości tej reakcji, jeśli temperatura zostanie obniżona z 25⁰C na 15^oC?

4. Ile razy wzrosła szybkość pewnej reakcji, jeśli jej temperaturowy współczynnik wynosi γ=3, a temperatura wzrosła o 5^oC?

γ = 5

∆T = 8

5. Ile razy wzrosła szybkość pewnej reakcji, jeśli jej temperaturowy współczynnik wynosi γ=4, a temperatura wzrosła o 8^oC?

6. Temperaturowy współczynnik pewnej reakcji wynosi γ=3. O ile stopni należy podnieść temperaturę, aby szybkość reakcji wzrosła 10 razy?

γ = 3 Temperaturowy współczynnik pewnej reakcji

∆T = ? Różnica temperatury

szybkość reakcji wzrosła

7. Temperaturowy współczynnik pewnej reakcji wynosi γ=4. O ile stopni należy podnieść temperaturę, aby szybkość reakcji wzrosła 3 razy?

γ = 4 Temperaturowy współczynnik pewnej reakcji

∆T = ? Różnica temperatury

szybkość reakcji wzrosła

8. Temperaturowy współczynnik pewnej reakcji wynosi γ=1. O ile stopni należy podnieść temperaturę, aby szybkość reakcji wzrosła 3 razy?

γ=1. nie wpływa na przyśpieszenie reakcji.

Zadanie . Obliczyć stałą szybkości reakcji k (enzymatycznych), jeżeli:

po 5 minutach stężenie substratu zmalało z 0,2 M do 0,05 M.

k =? stała szybkości reakcji

t - czas reakcji 5 min

a - stężenie początkowe substratu 0,2 M

(a-x) - stężenie substratu w danym momencie 0,05 M

Zawsze ilość substratu maleje a ilość produktu rośnie = < 1.

1. po 8 minutach stężenie substratu zmalało z 0,3 M do 0,15 M.

k =? stała szybkości reakcji

t - czas reakcji 8 min

a - stężenie początkowe substratu 0,3 M

(a-x) - stężenie substratu w danym momencie 0,15 M

1. po 30 s stężenie substratu zmalało z 0,02 M do 0,015 M.

k =? stała szybkości reakcji

t - czas reakcji 30s

a - stężenie początkowe substratu 0,02M

(a-x) - stężenie substratu w danym momencie 0,15M

W którym przypadku k miało najwyższą wartość? Podać jednostkę k.

Zadanie 3.

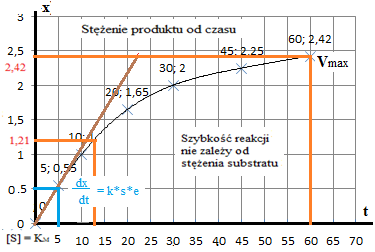
Wyznaczyć rząd reakcji oraz stałą szybkości k dla reakcji hydrolizy skrobi, wiedząc że po 5 min stężenie produktu wynosiło 0,55 mg/cm³, po 10 min - 1,00, po 20 ­1,65; po 30 - 2,00; po 45 - 2,25; po 60 - 2,42; po 90 - 2.42 mg/cm³. Wykreślić krzywe

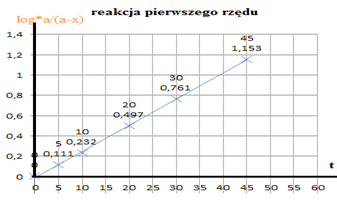
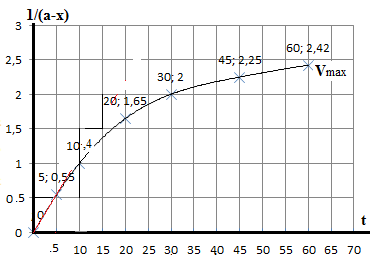
t (czas)	x (stężenie produktu)	a-x (stężenie substratu)	log*a/(a-x)	1/(a-x)
0	0	2,42	log*2,42/242 = 0	1 / 2,42 = 0,413
5	0,55	2,42 - 0,55 = 1,87	log*2,42/1.87 = 0,111	1 / 1,87 = 0,535
10	1	2,42 - 1 = 1,42	log*2,42/142 = 0,232	1 / 1,42 = 0,704
20	1,65	2,42 - 1,65 = 0,77	log*2,42/0,77 = 0,497	1 / 0,77 = 1,299
30	2	2,42 - 2 = 0,42	log*2,42/0,42 = 0,761	1 / 0,42 = 2,381
45	2,25	2,42 - 2,25 = 0,17	log*2,42/0,17 = 1,153	1/ 0,17 = 5,882
60	2,42	0	-	-
90	a = 2,42	0	-	-

Wyznaczyć rząd reakcji z treści zadania.

1. stężenia produktu od czasu x / t

2. szybkości reakcji od czasu Po przekształceniu obliczamy według wzoru v = x/t = 0,55 / 5 = 0,11.

Wyznaczamy graficznie, styczną do łuku.

Szybkość początkowa reakcji V₀ = x/t nie jest zależna od rzędu reakcji i mierzymy ją w punkcie pierwszym.

Wyznacz stałą szybkości k dla reakcji. Stała Michaelisa v = V max / 2

Szybkość reakcja enzymatycznej (zerowa V od S)

k - stała szybkość reakcji

S - stężenie substratu 1,87 M

e - stężenie enzymu 0,55 M

Stała Michaelisa v = V max / 2 = 2,42/2=1,12 połowa stężenia)

3. wartości log*a/(a-x) od czasu a = 2,42

4. wielkości 1/(a-x) od czasu

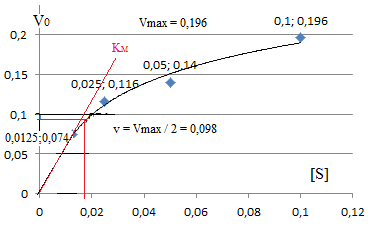
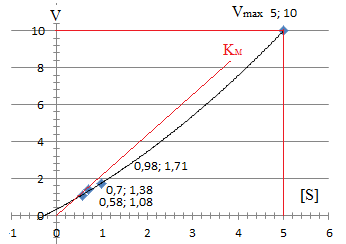
Zadanie 5. Prowadząc hydrolizę sacharozy o stężeniach 0,0125 - 0,1 M przy pomocy inwertazy drożdżowej, otrzymano w poszczególnych czasach reakcji następujące ilości glukozy i fruktozy [mg]:

Stężenie			Czas reakcji [min]
sacharozy [M]	[V0]	5	10	15	30
0,100	0,98/5=0,196	0,98	1,71	2,52	3,84
0,050	0,70/5=0,14	0,70	1,38	1,94	2,76
0,025	0,58/5=0,116	0,58	1,08	1,48	2,21
0,0125	0,37/5=0,074	0,37	0,55	0,82	0,86

Na podstawie podanych wyników:

1. Wyznaczyć stałą Michaelisa-Menten Wyznaczyć szybkości początkowe dla każdego stężenia substratu, wykreślić krzywą Michaelisa-Menten (zależność szybkości początkowych od stężenia substratu) i wyznaczyć stałą Michaelisa-Menten

Stężenie
sacharozy [S]	[V0]
0,10	0,98/5=0,196
0,05	0,70/5=0,14
0,025	0,58/5=0,116
0,0125	0,37/5=0,074
Szybkość początkowa wynosi 0,074 min^-1

2. Wykreślić krzywą Lineweavera-Burka dla zależności od 1I[S] i wyznaczyć stałą Michaelisa-Menten oraz szybkość maksymalną V_M

Stężenie sacharozy [M]	[V0]	1 [S]	1 [V0]
0,100	0,98/5=0,196	5	10
0,050	0,70/5=0,14	0,98	1,71
0,025	0,58/5=0,116	0,70	1,38
0,0125	0,37/5=0,074	0,58	1,08










Zadanie 6.

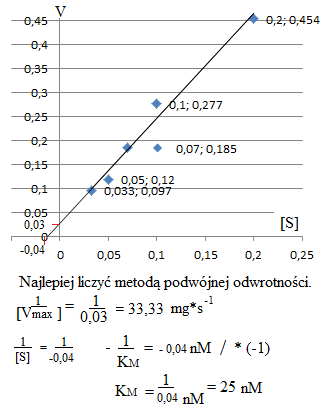
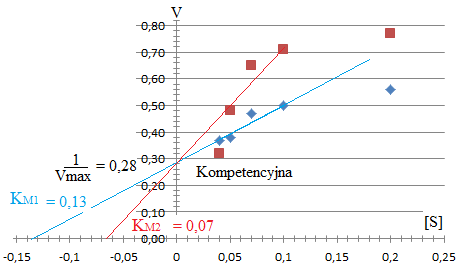
Oznaczono szybkości początkowe Vo dla reakcji enzymatycznej przy różnych stężeniach substratu:

Początkowe stężenie substratu [mM] [S]	Szybkość początkowa Vo [mg,s'^l] [v]	Gdy nie mamy V max.
				1 [S]	1 [V0]
5 10 15 20 30	2,2 3,6 5,4 8,3 10,3	1 : 5 = 0,20 1 : 10 = 0,10 1 : 15 = 0,07 1 : 20 = 0,05 1 : 30 = 0,033	1 : 2,2 = 0,454 1 : 3,6 = 0,277 1 : 5,4 = 0,185 1 : 8,3 = 0,120 1 : 10,3 = 0,097

Wartość szybkości maksymalnej V _max = 132 mg·s^-1. Obliczyć K_M oraz podać dla jakiego stężenia substratu szybkość reakcji osiąganie wartości maksymalną.















Zadanie 7.

Po 5 min reakcji przereagowała połowa substratu o początkowym stężeniu 4 . 10.⁵ mol·dm^-3. Szybkość maksymalna reakcji wynosiła 2,04 *10^-5 M·min^-1. Obliczyć K_M oraz stężenie produktu po 10 min.

1. t = 5 min / połowa substratu / po 10 min

2. [S] = 4* 10^-5 mol * dm ^-3.

3. V max = 2,04 *10^-5 M·min^-1

4. k = ?

5. v = ?

6. K_M = ?










Stężenie produktu po 10 min?

1. t = 10 min

2. [S] = 4* 10^-5 mol * dm ^-3.

3. k = 0,135 min^-1

4. = ( a - x) stężenie substratu po 10 min

5. x = ? stężenie produktu po 10 min










zamiana miejscami


























stężenie substratu po 10 min

4 * 10^-5 -x = 1,038 * 10^-5

x = 4 * 10^-5 - 1,038*10^-5

x= 2,962*10^-5

Po 10 min powstało 2,962*10^-5 mol.*dm³ produktu.






Zadanie 8.

Stała Michaelisa w reakcji hydrolizy peptydu wynosi 4 . 10^-3 M. Przy stężeniu początkowym substratu 8 . 10^-5 M, po 2 minutach zhydrolizowało 10% peptydu. Obliczyć stałą szybkości reakcji oraz szybkość maksymalną V_max

zhydrolizowało 10% peptydu to pozostało 90%.

[S₂] = (a-x) 90% z 8 = 0,9 * 8 * 10^-5 = 7,02 * 10^-5

K_M = 4*10^-3 M

[S] = 8*10^-5

k = ?

v = ?




















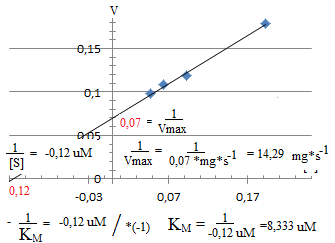
Zadanie 9. Określono szybkości początkowe działania enzymu na substrat przy różnych stężeniach substratu:

Początkowe stężenie substratu [µM]	Vo [mg·s·^l]	1 [S]	1 [Vo}
5,2 10,8 15,6 20,8	5,6 8,4 9,3 10,3	0,192 0,093 0,064 0,048	0,179 0,119 0,108 0,098

Czynniki wpływające na szybkość reakcji.




Zadanie 2. W wyniku działania dwóch różnych enzymów na substrat o zmiennym stężeniu określono szybkości początkowe:

Początkowe stężenie substratu [μM]	enzym A	enzym B
		v0	v0
50 100 156 208	5,6 8,4 9,3 10,3	11,2 14,9 16,8 18,7

1. Określić stałe kinetyczne K_M i V_max.

2. Który z enzymów wykazuje większe powinowactwo do substratu?

Zadanie 3.

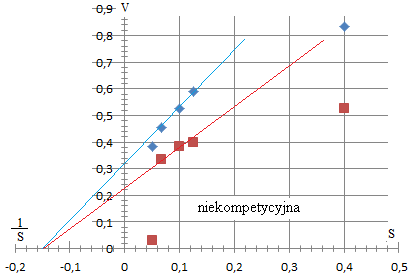
Zmierzono szybkości początkowe przy różnym stężeniu substratu dla reakcji katalizowanej przez trypsynę niemodyfikowaną i modyfikowaną:

Początkowe stężenie substratu [μM]	enzym niemodyfikowany	enzym modyfikowany		E nie mod.	E mod
		v0	v0	1 S	1 V0	1 V0
4 8 10 15 20	1,2 1,7 1,9 2,2 2,6	1,9 2,5 2,6 3,0 3,2	0,4 0,125 0,1 0,067 0,05	0,833 0,588 0,526 0,454 0,384	0,526 0,4 0,384 0,333 0,0312

1. Określić stałe kinetyczne K_M i V_max.





odp - K_M się nie zmienia, nie ma wpływu na stęrzenie.

2. Jakiego rodzaju inhibicję wywołała modyfikacja trypsyny?

Odp: modyfikacja trypsyny wywołała modyfikację niekompetycyjną.

Zadanie 4.

Oznaczono szybkości początkowe reakcji bez i z dodatkiem inhibitora. Otrzymano:

Początkowe stężenie substratu [μM]	bez inhibitora	działanie inhibitora		E mod	E nie mod.
		v0	v0	1 V0	1 V0	1 V0
5 10 15 20 26	1,8 2,0 2,4 2,6 2,7	1,3 1,4 1,8 2,1 3,1	0,2 0,1 0,07 0,05 0,04	0,56 0,50 0,47 0,38 0,37	0,77 0,71 0,65 0,48 0,32

1. Wyznaczyć stałe kinetyczne.







2. Określić rodzaj inhibicji - kompetencyjna

3. Podać w jaki sposób można cofnąć działanie inhibitora.

Jeśli mamy inhibicję kompetencyjną to przeciwdziałamy dodając substrat.

Jeśli mamy inhibicję niekompetencyjną to dodając drobnocząsteczkowy substrat wiążąc inhibitor.

9























































---