WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM FIZYCZNE

Grupa szkoleniowa: E3X1S1 Podgrupa: 2

Daniel Ilczyszyn

Kamil Graczyk

Sprawozdanie z Pracy Laboratoryjnej nr 24

Temat pracy: Badanie rezonansu w obwodach elektrycznych

I. Wstęp teoretyczny

Rezonansem nazywamy zjawiska szybkiego wzrostu amplitudy drgań układu fizycznego, gdy częstotliwość zewnętrznych drgań wymuszających jest zbliżona do częstotliwości drgań własnych układu.

Drganiami nazywamy taki proces, w którym wielkości fizyczne na przemian rosną i maleją. Szczególnym przypadkiem są drgania harmoniczne, które powstają, gdy siła sprowadzająca układ w położenie równowagi jest proporcjonalna do wychylenia. Rozróżnić można drgania swobodne, wymuszone i tłumione.

W rozważaniach na temat rezonansu będziemy badali co się dzieje z układem, gdy działa na niego siła harmoniczna w postaci: F = F₀ cos (ωt). Zjawisko rezonansu w obwodzie RLC możemy wywołać poprzez zmianę częstości pulsacji zasilania przy stałych wartościach R, L, C, lub przy stałej pulsacji przez zmianę elementów obwodu L i C.

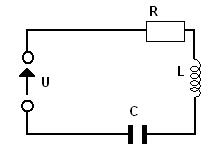
Układ rezonansowy RLC

Cel ćwiczenia:

Celem ćwiczenia jest zbadanie rezonansu w obwodzie elektrycznym RLC.

Potrzebne wzory:

1. Dobroć układu:
   

2. Częstotliwość rezonansowa:
   

3. Pasmo częstotliwości obwodu:
   

4. Napięcie na kondensatorze:
   
   , gdzie x to częstotliwość względna liczona względem częstotliwości rezonansowej f_r .

Opis układu pomiarowego:

Układ pomiarowy składa się:

• z generatora napięcia sinusoidalnego o przestrajalnej częstotliwości,

• woltomierza z sondą,

• pudełka z obwodami rezonansowymi z dołączonymi do niego trzema wymiennymi kondensatorami do wtyków C_X

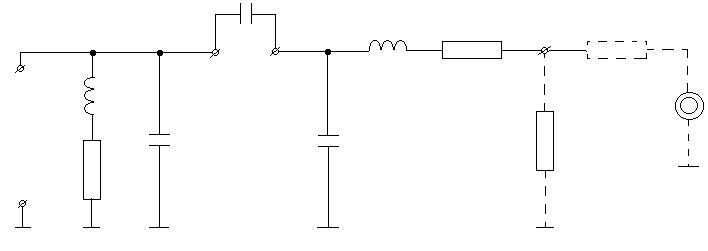
UE=2,5V

Schemat pomiarowy

Będziemy mierzyć wartości napięcia U_C dla różnych częstotliwości oraz wyznaczamy dobroć układu Q oraz pasmo B i wykreślimy zależność napięcia U_C w zależności od częstotliwości.

II. Opracowanie wyników pomiarów

Tabela pomiarowa:

Lp.	f [Hz]	U1 [V]	U2 [V] dla C1= 82 pF	U3 [V] dla C2= 130 pF	U4 [V] dla C3= 240 pF
1.	13000	0,91	0,01	0,12	0,35	-0,0780
2.	13100	1,00	0,02	0,16	0,47	-0,0709
3.	13200	1,11	0,11	0,20	0,64	-0,0638
4.	13300	1,24	0,14	0,28	0,92	-0,0567
5.	13400	1,41	0,18	0,38	1,35	-0,0496
6.	13500	1,61	0,25	0,53	1,94	-0,0426
7.	13600	1,86	0,36	0,79	2,45	-0,0355
8.	13700	1,88	0,53	1,21	2,39	-0,0284
9.	13800	2,29	0,82	1,79	2,12	-0,0213
10.	13900	2,87	1,28	2,23	1,94	-0,0142
11.	14000	3,72	1,79	2,23	1,92	-0,0071
12.	14100	4,42	1,94	2,13	2,02	0,0000
13.	14200	4,41	1,88	2,12	2,22	0,0071
14.	14300	3,73	1,79	2,09	2,34	0,0142
15.	14400	2,93	1,52	1,79	2,04	0,0213
16.	14500	2,31	1,10	1,29	1,51	0,0284
17.	14600	1,87	0,74	0,89	1,10	0,0355
18.	14700	1,56	0,49	0,61	0,77	0,0426
19.	14800	1,34	0,34	0,43	0,57	0,0496
20.	14900	1,17	0,24	0,32	0,43	0,0567
21.	15000	1,02	0,18	0,24	0,33	0,0638

1. Wyznaczenie częstotliwości rezonansowej

Zmieniając stopniowo częstotliwość sygnału podawanego z generatora, ustalono maksymalną. wartość mierzonego napięcia U₁. Częstotliwość, przy której U₁ = U_1max określana jest mianem częstotliwości rezonansowej i oznaczamy ją symbolem: f_r.

Wartość f_r, określona w ćwiczeniu wynosi:

f_r = 14,1 kHz

2. Wykreślenie zmierzonej zależności U₁(x), gdzie x jest częstotliwością względną.

Obliczam wartości x , dla częstotliwości f = 13000 Hz do 15000 Hz. (Wyniki załączone w tabeli pomiarowej powyżej )

Wykres U₁(x) (krzywa rezonansowa bez kondensatora) - załącznik nr 1

3. Wyznaczenie dobroci układu Q

Dobroć układu równa jest wartości wyrażenia
. Gdzie U_X jest wartością maksymalną odczytaną z poprzedniego wykresu, a wartość U₀ = 2,5V.

4. Wyznaczenie pasma częstotliwości B

Właściwości filtracyjne obwodu rezonansowego polegają na znacznym wzroście amplitudy napięcia wyjściowego, jeśli częstotliwość napięcia podawanego na obwód leży w paśmie częstotliwości B. Wyznaczenie wartości pasma B, ma więc bardzo duże znaczenie przy rozpatrywaniu obwodów rezonansowych.

Wielkość tę określamy jako stosunek częstotliwości rezonansowej f_r do dobroci układu Q

5. Przedstawienie zależności
dla obwodów z kondensatorami o pojemnościach:

• U₂ dla C₁ = 82 pF

• U₃ dla C₂ = 130 pF

• U₄ dla C3 = 240 pF

Wykres U(f) - załącznik nr 2

III. Wnioski

W momencie rezonansu szeregowego wartość napięcia U1 jest maksymalna równa iloczynowi napięcia U₀ i dobroci obwodu Q. Na podstawie tych wykresów mogę z dużym przybliżeniem określić wartość częstotliwości rezonansowej. Wartość ta dla danych odczytanych z wykresów wynosi 14100 [Hz]. Na podstawie wartości elementów wynosi 14721 [Hz].
Ewentualne rozbieżności wynikają stąd iż wzory te są prawdziwe jedynie dla idealnych elementów R,L,C a tu mają 5% tolerancję, przy uwzględnieniu jej, częstotliwość zmienia się w zakresie od 14020 do 15496 Hz.

W obwodzie pojedynczym (bez kondensatorów) kształt krzywej rezonansowej jest dzwonowaty o łagodnych zboczach . W obwodach sprzężonych wartość napięcia U jest mniejsza co widać na wykresie i zależna od stopnia sprzężenia które reguluje C_X. Mamy trzy rodzaje sprzężeń.

Dla C₁ = 82pF amplituda jest mniejsza niż dla obwodu pojedynczego, występuje jeden punkt ekstremalny oraz
z tego wynika, że w tym wypadku mamy do czynienia ze sprzężeniem podkrytycznym. Dla C₂ = 130pF charakterystyka przy wierzchołku jest bardziej płaska i ma bardziej strome zbocza. Dla C₃=240pF wykres posiada trzy punkty ekstremalne takie sprzężenie nazywamy nadkrytycznym. W tym przypadku zwiększa się jeszcze nachylenie charakterystyki na krawędziach pasma natomiast tracimy na amplitudzie , która zmniejsza się do połowy w porównaniu z obwodem pojedynczym.

Trudno jest także na podstawie takich pomiarów jakich dokonaliśmy na pracowni określić te wartości z dużą dokładnością, a ponadto podczas przeprowadzania pomiarów wyraźnie był widoczny wpływ przyrządów pomiarowych na badany układ Dlatego mogliśmy jedynie określić wartości przybliżone. Pomimo tego różnice pomiędzy wartościami obliczonymi a zmierzonymi są niewielkie.

Załącznik 1

Załącznik 2

Załącznik 3- wykres zależności Uc(f)

BNC

Do generatora

U₁

R

R

L

R

C

R

L

C

Cx

U₂

E

---