Data ćwiczeń 18.11.2004
Fizyka Eksperymentalna |
||
ćw. 24 - Badanie efektu Halla |
||
Zespół numer 20
|
||
R.A 2004/05 |
Grupa 4 |
Semestr III |
Politechnika Warszawska
Wydział Inżynierii Lądowej
Semestr III Grupa 4
1. Podstawy fizyczne
Aby poprawnie wykonać dane ćwiczenie, należy zapoznać się z podstawowymi pojęciami i zjawiskami fizycznymi, bez zrozumienia których, nie będziemy w stanie poprawnie wykonać i zrozumieć wykonywanego ćwiczenia.
W doświadczeniu zajmiemy się badaniem zjawiska Halla, które zaobserwujemy przy użyciu przyrządu, którego nazwa wzięła się od nazwiska konstruktora. Hallotron, jest to warstwa półprzewodnika naparowana na nieprzewodzące podłoże o bardzo niewielkiej grubości d = (100±1)μmi zaopatrzona w cztery elektrody. Prąd sterujący I halotronu przepływa wzdłuż naparowanej warstwy o długości l, a więc przez przekrój dc gdzie c = (2,5±0,1)μm - szerokość naparowanej warstwy.
Półprzewodniki charakteryzują się tym, że ich Eg = 0,1eV…5eV. Poniżej dolej granicy są to już przewodniki, a powyżej górnej - izolatory. Półprzewodniki mogą posiadać nośniki prądu, którymi mogą być swobodne elektrony lub dziury. Elektrony są to nośniki prądu obdarzone ładunkiem ujemnym, natomiast dziury są to nośniki o znaku dodatnim. Półprzewodniki, np. krzem, german mogą być samoistne bądź domieszkowane. Półprzewodniki samoistne w niskiej temp. są izolatorami, ponieważ pasmo przewodnictwa jest puste, ale wzrost temperatury może spowodować wzrost energii wystarczającej do przeskoku elektronów przez pasmo wzbronione. Domieszkowanie natomiast polega na wprowadzeniu do sieci krystalicznej półprzewodnika atomów obcego pierwiastka.
Na nośniki prądu w halotronie, działa prostopadła do kierunku przepływu prądu sterującego IS, oraz indukcji B, siła Lorentza FL. Pod jej wpływem w czasie przepływu prądu przez płytkę (wykonaną z przewodnika lub półprzewodnika) zmienia się tor nośników prądu:
F= q v x B
gromadzą się one, na powierzchni bocznego przekroju warstwy tak długo dopóki działanie ich pola elektrycznego nie skompensuje siły Lorentza. Obecność zgromadzonych ładunków można wykryć mierząc różnicę potencjałów Uh, która to właśnie jest napięciem Halla, między bocznymi powierzchniami naparowanej warstwy halotronu. Na jednej z tych powierzchni gromadzą się właśnie ładunki spychane tam siłą Lorentza, co jest widoczne na poniższym rysunku:
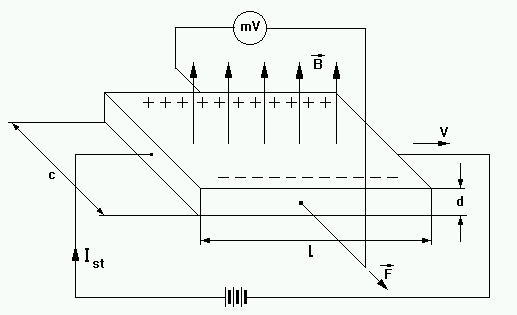
Zgromadzone przy ściankach bocznych ładunki wytwarzają pole elektryczne (zakładamy, że jednorodne) o natężeniu Uh/c, które działa na ładunki nośników prądu sterującego q siłą F=q Uh/c. W warunkach równowagi F=FL, a więc q Uh/c = q v B, gdy kierunek prądu sterującego jest prostopadły do wektora indukcji B. Stąd otrzymujemy
Prędkość nośników prądu jest tym większa im większe jest natężenie prądu sterującego Is płynącego przez halotron i im mniejsza jest koncentracja n nośników prądu w półprzewodniku. Z definicji natężenia prądu jako strumienia ładunków mamy
e - ładunek elementarny (ładunek nośnika prądu)
Podstawiając v z powyższego wzoru do wzory na napięcie Halla, mamy:
Pomiar napięcia Halla pozwala wyznaczyć koncentrację nośników w próbce pod warunkiem, ze poruszają się w niej tylko nośniki jednego znaku. W dalszych rozważaniach przyjmiemy, że w naszym halotronie dominują nośniki jednego znaku tak silnie, że możemy pominąć wpływ pozostałych na wartość napięcia Halla i na rezystancję Rh próbki.
Z prawa Ohma i z definicji natężenia prądu Is, mamy:
µ - ruchliwość nośników prądu
U - spadek napięcia wzdłuż halotronu.
U/l - jest to natężenie pola elektrycznego w warstwie w kierunku prądu sterującego
µ∙U/l - jest to średnia prędkość ruchu nośników tego prądu w kierunku pola
Z dwóch powyższych wzorów możemy wyznaczyć koncentrację n i ruchliwość µ przez łatwo mierzalne wielkości; wzory te przyjmują następującą postać:
Zatem ze wzorów na koncentrację n i ruchliwość µ wynika, że napięcie Halla Uh jest wprost proporcjonalna do iloczynu natężenia prądu sterującego Is lub napięcia U przyłożonego do warstwy i indukcji magnetycznej B.
Z tych wzorów wynika także to, iż iloczyn koncentracji n i ruchliwości µ jest odwrotnie proporcjonalny do rezystancji warstwy Rh. Podstawiając, bowiem U = RhIs (z prawa Ohma) do wzoru na ruchliwość µ otrzymujemy:
- iloczyn n∙e∙µ nazywamy przewodnictwem właściwym warstwy
- iloraz 1/n•e - stałą Halla
2. Cele ćwiczenia
a) Badanie proporcjonalności napięcia Halla Uh do natężenia prądu sterującego Is i spadku napięcia U na halotronie. Wyznaczenie koncentracji nośników n i ich ruchliwości m.
Budujemy układ według schematu: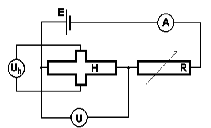
Przeprowadziliśmy badanie, które miało na celu wykazanie, jak zmienia się napięcie Halla Uh w zależności od prądu sterującego Is oraz od wartości pola magnetycznego B. Zmieniające się wraz z Is napięcia Uh i U przedstawione zostały w tabelach i na wykresach Uh od Is oraz Uh od U:
Tabele z wynikami przeprowadzonych badań:
Dla IB = 0 Dla IB = 1,4 B = 112[mT]
Lp. |
I [mA] |
U [V] |
UH [V] |
|||
1 |
3,2 |
-0,541 |
0 |
|||
2 |
3,4 |
-0,581 |
0 |
|||
3 |
3,7 |
-0,628 |
0 |
|||
4 |
4,0 |
-0,683 |
0 |
|||
5 |
4,4 |
-0,748 |
0 |
|||
6 |
4,9 |
-0,828 |
0 |
|||
7 |
5,5 |
-0,927 |
0 |
|||
8 |
6,3 |
-1,052 |
0 |
|||
9 |
7,3 |
-1,217 |
0 |
|||
10 |
8,7 |
-1,444 |
0 |
|||
11 |
10,4 |
-1,713 |
0 |
|||
Lp. |
I [mA] |
U [V] |
UH [V] |
|||
1 |
3,2 |
-0,543 |
-21,5 |
|||
2 |
3,4 |
-0,584 |
-23,2 |
|||
3 |
3,7 |
-0,631 |
-25,1 |
|||
4 |
4,0 |
-0,686 |
-27,3 |
|||
5 |
4,4 |
-0,752 |
-29,9 |
|||
6 |
4,9 |
-0,832 |
-33,0 |
|||
7 |
5,5 |
-0,930 |
-37,1 |
|||
8 |
6,3 |
-1,057 |
-42,0 |
|||
9 |
7,3 |
-1,222 |
-48,5 |
|||
10 |
8,7 |
-1,450 |
-57,8 |
|||
11 |
10,4 |
-1,723 |
-68,4 |
|||
Dla IB = 1,7 B =134[mT] Dla IB = 2 B = 154[mT]
Lp. |
I [mA] |
U [V] |
UH [V] |
|||
1 |
3,2 |
-0,550 |
-25,4 |
|||
2 |
3,4 |
-0,591 |
-27,4 |
|||
3 |
3,7 |
-0,639 |
-29,6 |
|||
4 |
4,0 |
-0,695 |
-32,2 |
|||
5 |
4,4 |
-0,761 |
-35,3 |
|||
6 |
4,9 |
-0,842 |
-39,0 |
|||
7 |
5,5 |
-0,942 |
-43,6 |
|||
8 |
6,3 |
-1,065 |
-49,6 |
|||
9 |
7,3 |
-1,231 |
-57,3 |
|||
10 |
8,7 |
-1,459 |
-67,9 |
|||
11 |
10,4 |
-1,728 |
-80,8 |
|||
Lp. |
I [mA] |
U [V] |
UH [V] |
|||
1 |
3,2 |
-0,547 |
-29,5 |
|||
2 |
3,4 |
-0,588 |
-31,7 |
|||
3 |
3,7 |
-0,636 |
-34,3 |
|||
4 |
4,0 |
-0,691 |
-37,3 |
|||
5 |
4,4 |
-0,758 |
-40,9 |
|||
6 |
4,9 |
-0,838 |
-45,3 |
|||
7 |
5,5 |
-0,937 |
-50,6 |
|||
8 |
6,3 |
-1,064 |
-57,4 |
|||
9 |
7,3 |
-1,231 |
-66,5 |
|||
10 |
8,7 |
-1,459 |
-78,7 |
|||
11 |
10,4 |
-1,747 |
-93,5 |
|||
Dla IB = 2,3 B = 172[mT]
Lp. |
I [mA] |
U [V] |
UH [V] |
1 |
3,2 |
-0,549 |
-33,7 |
2 |
3,4 |
-0,590 |
-36,2 |
3 |
3,7 |
-0,638 |
-39,1 |
4 |
4,0 |
-0,693 |
-42,5 |
5 |
4,4 |
-0,760 |
-46,6 |
6 |
4,9 |
-0,840 |
-51,6 |
7 |
5,5 |
-0,940 |
-57,7 |
8 |
6,3 |
-1,067 |
-65,6 |
9 |
7,3 |
-1,233 |
-75,8 |
10 |
8,7 |
-1,462 |
-80,0 |
11 |
10,4 |
-1,737 |
-106,9 |
W doświadczeniu zostały wykorzystane następujące mierniki prądu i napięcia:
Nazwa |
Zakres |
Błąd pomiaru |
Miliamperomierz |
200mA |
±1,2%rdg+1dgt |
Woltomierz |
2V |
±0,5%+1dgt |
Woltomierz (na halotronie) |
200mV |
±0,5%+1dgt |
rdg- wartość pomiaru
1dgt- wartość ostatniej cyfry odczytu
Prostokąty niepewności na wykresach zostały obliczone w następujący sposób:
ΔUh = zakres • klasa = 200mV • 0,5% = ± 1mV
ΔIs = zakres • klasa = 200mA • 0,5% = ± 0,1mA
ΔU = zakres • klasa = 2V • 0,5% = ± 0,01V
b) pomiar rezystancji halotronu
Budujemy układ jak na rysunku:
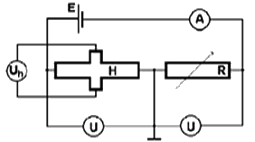
Powstał w ten sposób dzielnik napięć utworzony przez halotron H i opornicę R. Napięcia na tych elementach dzielnika mierzone są przez dwa identyczne woltomierze V. Dobieramy rezystancję opornicy R (około 250 W) tak by oba woltomierze V wskazywały to samo napięcie. Wówczas rezystancja opornicy równa jest rezystancji halotronu.
Możemy również obliczyć rezystancję halotronu ze wzoru:
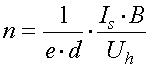
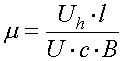
podstawiając do powyższego wzoru koncentrację n oraz ruchliwość µ:
c) Badanie zależności koncentracji n i ruchliwości µ oraz rezystancji halotronu Rh od temperatury T:
Halotron umieszczony w polu magnetycznym elektromagnesu i ustalamy wielkość natężenia prądu elektromagnesu IE (B = const.).
Umieszczamy termoparę w górnym otworze miedzianej obudowy halotronu i łączymy z miernikiem temperatury T. Regulujemy miernik tak by wskazywał temperaturę pokojową. W dolnym otworze obudowy miedzianej umieszczamy grzałkę i łączymy ją z zasilaniem. Nastawiamy regulator temperatury na wybraną temperaturę i rozpoczynamy grzania.
Po ustaleniu się temperatury mierzymy rezystancję halotronu Rh, natężenie prądu sterującego Is oraz napięcie Uh i spadek napięcia U na halotronie. Przedstawiamy zmierzone i obliczone wartości Rh i n wartości µ w funkcji temperatury T przedstawiamy w logarytmicznym układzie współrzędnych.
Jeżeli punkty leżą na prostych to wyznaczamy ich współczynniki kierunkowe i obliczamy przerwę energetyczną ∆E półprzewodnika oraz wykładnik potęgi m opierając się na teoretycznych zależnościach:
k - stała Boltzmana
d) obliczamy n oraz ∆n
Do obliczenia wartości koncentracji nośników zastosowaliśmy wzór:
![]()
gdzie: ![]()
Jednostka jest następująca:
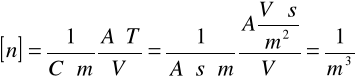
Dane potrzebne do obliczeń:
grubość hallotronu: d = (100 ± 1) μm
szerokość: c = (2,5 ± 0,1) mm
długość: l = (10,0 ± 0,1) mm
ładunek elektronu: e = 1,6•10-19 [C]
Zależności ![]()
przedstawione na załączonych wcześniej wykresach pozwoliły nam obliczyć współczynnik kierunkowy a:
![]()
Wykorzystując otrzymane wartości możemy obliczyć koncentrację nośników:
![]()
Podstawiając dane do powyższego wzoru otrzymujemy wynik:
dla B = 112mT , a = 6,72 , n = 1,04•1021
dla B = 134mT , a = 7,93 , n = 1,05•1021
dla B = 154mT , a = 9,19 , n = 1,04•1021
dla B = 172mT , a = 10,38 , n = 1,03•1021
Błąd koncentracji Δn policzyliśmy ze wzoru:
![]()
ΔB = 0,13 [mT]
Δn = 0,01•1021![]()
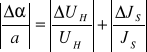
a więc błąd względny obliczony ze wzoru:
![]()
wyniósł:
Δnwzg = 1,0%
Otrzymaliśmy wynik końcowy:
n = (1,04±0,01)•1021![]()
e) badanie dodatkowe
Przy okazji obliczania wartości koncentracji wykazaliśmy, że mimo różnych indukcji magnetycznych B, rozkład natężenia prądu sterującego Is oraz napięcia Halla Uh był taki, że koncentracja n dla danej temperatury pokojowej (około 200C) była niezmienna.
3. Dyskusja niepewności pomiarowej
Niepewności pomiarowe:
niedoskonałość badanego obiektu
ograniczona dokładność przyrządów pomiarowych
niedoskonałość ludzkich zmysłów
Błędy pomiarowe:
wadliwy przyrząd pomiarowy
nieuwaga obserwatora
Niepewność pomiarowa Δn to połowa szerokości przedziału, w którym mieści się rzeczywista wartość wielkości mierzonej.
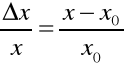
Niepewność bezwzględna: ![]()
Niepewność względna:
Niepewności pomiarowe mogą być:
- przypadkowe (rozrzut wyników występujący przy powtarzaniu pomiarów, którego nie można usunąć)
- systematyczne (odchylenie mierzonej wartości w tę samą stronę, np. błąd miejsca zero)
Szacownie niepewności pomiarowej:
- mała ilość pomiarów (do 3)
Szacujemy, że Δx wynosi połowę wartości najmniejszej podziałki przyrządu pomiarowego, lub Δx obliczamy z klasy przyrządu ze wzoru:
![]()
- wielokrotny pomiar (powyżej 3)
Stosujemy rozkład Gaussa:
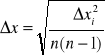
∆xi - odchylenie i-tego pomiaru od wartości średniej
n - liczba pomiarów
- niepewność pomiarowa wielkości złożonej
Jeżeli wynik pomiaru y jest przedstawiony za pomocą wzoru:
y = f (x1, x1), to niepewność Δy wyniku pomiaru jest równa:
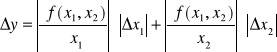
Wnioski i spostrzeżenia własne
Podczas wykonywania ćwiczenia zauważyliśmy, że napięcie Halla zależy wprost proporcjonalnie od natężenia prądu sterującego Is oraz od indukcji pola magnetycznego B, w którym znajdował się halotron. Podczas stopniowej zmiany na mniejszy oporu za pomocą opornicy dekadowej, natężenie prądu sterującego Is rosło, co jednocześnie powodowało wzrost napięcia Halla. Dzięki zaobserwowanym zjawiskom możemy stwierdzić, że teoretyczne założenia dotyczące hallotronu, mianowicie gromadzenia się ładunków przeciwnych znaków po przeciwnych stronach półprzewodnika znalazły oparcie w praktyce, Nasze badanie potwierdziło istnienie napięcia Halla oraz pozwoliło na wyznaczenie koncentracji n nośników w badanej próbce.
Zjawisko pojawiania się napięcia Halla zostało doskonale wykorzystane w technice, dzięki temu zjawisku powstało wiele pożytecznych przyrządów m.in. teslomierze halotronowe, czyli mierniki indukcji magnetycznej lub bezstykowe przełączniki sygnałów elektrycznych bądź wyspecjalizowane sondy halotronowe.
7
![]()
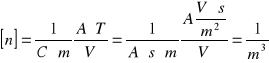
Wyszukiwarka
Podobne podstrony:
sprawozdanie z Halla, Studia, II rok, Fizyka Eksperymentalna
24 - Sprawozdanie z Halotronu poprawione, Studia, II rok, Fizyka Eksperymentalna
sprawozdanie 24, Studia, II rok, Fizyka Eksperymentalna
Braja 24, Studia, II rok, Fizyka Eksperymentalna
sprawozdanie12, Studia, II rok, Fizyka Eksperymentalna
sprawozdanie fizyka, Studia, II rok, Fizyka Eksperymentalna
Lab Fiz322a, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 31, Studia, II rok, Fizyka Eksperymentalna
Spr 42, Studia, II rok, Fizyka Eksperymentalna
Fizyka1, Studia, II rok, Fizyka Eksperymentalna
Cwiczenie 19, Studia, II rok, Fizyka Eksperymentalna
protokół fiza, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 35, Studia, II rok, Fizyka Eksperymentalna
FIZLAB~1, Studia, II rok, Fizyka Eksperymentalna
więcej podobnych podstron