Sprawozdanie z laboratorium z Podstaw Automatyki		Autorzy: Mazur Mateusz Pałosz Tomasz
Data: 18.05.2oo6 r.	Temat: Regulacja trójpołożeniowa

1. Regulacja trójpołożeniowa bez korekcji.

rys.1.1. Schemat regulacji trójpołożeniowej bez korekcji.

rys.1.2. Przebieg czasowy regulacji trójpołożeniowej bez korekcji.

Przebieg oscylacji wyjścia (y jasna niebieska linia) układu zmniejsza amplitude. Istnieje jednak pewna granica zmniejszania amplitudy zależna od parametrów strefy nieczułości a oraz histerezy h. Minimalny czas wartości 1 oraz -1 wyjścia z regulatora wynosi h, natomiast minimalny czas wartości 0 wynosi a. Zatem im mniejsze wartości a oraz h tym lepsza regulacja.

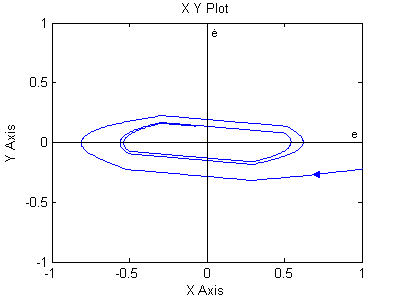
rys.1.3. Wykres trajektorii fazowej dla regulacji trójpołożeniowej bez korekcji.

Z wykresu widać, że wartość wyjścia y oscyluje wokół wartości zadanej. Na osi e widać wartość a+h natomiast na osi
widać wartość h. Po pewnym czasie oscylacje ustalają się na stałym poziomie i układ krąży po stałej trajektorii ograniczonej przez minimalne wartości a oraz h.

2. Regulacja trójpołożeniowa z korekcją PI.

rys.2.1. Schemat regulacji trójpołożeniowej z korekcją PI. k = 1; T1 = 0.5;

rys.2.2. Przebiegi czasowe regulacji trójpołożeniowej z korekcją PI.

W tym przypadku jakość regulacji zależy od histerezy h, ponieważ regulator nie przyjmuje wartości -1. Im mniejsza jest histereza tym wartość wyjściowa będzie bliższa wartości zadanej. Oczywiście parametry k oraz T1 wpływają na czas narastania oraz na odchylenie.

rys.2.3. Wykres trajektorii faz regulacji trójpołożeniowej z korekcja PI.

Wartość wyjściowa zmierza w kierunku wartości zadanej praktycznie liniowo. Przekracza ją i osiąga wartość maksymalną. Następnie nie zmniejsza się tylko pozostaje na stałym poziomie. Zatem nie występuje tutaj przeregulowanie. Należy trafić w punkt na trajektorii fazowej tak, aby znajdował się on najbliżej wartości zadanej.

3. Regulacja trójpołożeniowa ze sprzężeniem zwrotnym prędkościowym.

rys.3.1. Schemat regulacji trójpołożeniowej ze sprzężeniem zwrotnym prędkościowym. kt=6.

rys.3.2. Przebiegi czasowe regulacji trójpołożeniowej ze sprzężeniem zwrotnym prędkościowym.

W powyższym przypadku wartość wyjściowa w niewielkim stopniu zależy od histerezy i strefy nieczułości.

rys.3.3. Wykres trajektorii fazowej regulacji trójpołożeniowej ze sprzężeniem zwrotnym prędkościowym.

Portret fazowy umożliwia ocenić stabilność układu, określić przeregulowanie, stwierdzić czy występujące przebiegi są aperiodyczne, czy oscylacyjne.

W przypadku regulacji trójpołożeniowej portret fazowy podzielony jest na 3 części (w przypadku regulatorów rzeczywistych z histerezą osobno pod i nad osią OX). Proste rozdzielające te części nazywane są osiami komutacji. Widać, że sprzężenie prędkościowe (tachometryczne) ma wpływ na nachylenie osi komutacji układu, pozwala na uzyskanie takiego samego okresu drgań własnych przy zwiększonym współczynniku tłumienia - szybsze zanikanie stanów dynamicznych, powodując jednak powstawanie błędów statycznych. Na powyższych wykresach widać również, że szerokość histerezy regulatora trójpołożeniowego ma wpływ na amplitudę drgań sygnału wyjściowego powodując jednocześnie „zacieśnienie” obrazu fazowego. Czas całkowania pozwala na wyprowadzenie układu z cyklu granicznego.

---