UKŁADY WSPÓŁRZĘDNYCH PŁASKICH

Układ współrzędnych 2000 (2000 r)

Dla opracowań katastralnych i przy opracowaniu mapy zasadniczej w skali 1:5 000 i skalach większych stosuje się odwzorowanie Gaussa-Krügera tworzące cztery układy współrzędnych płaskich prostokątnych, oznaczone symbolami: "2000/15", "2000/18", "2000/21" i  "2000/24",  w systemie GRS-80.

Współrzędne płaskie prostokątne x, y są obliczane w odwzorowaniu Gaussa-Krügera w pasach trzystopniowych o południkach osiowych:15°, 18°, 21°, 24°. Pasy ponumerowane są: 5, 6, 7, 8 (rys.13). Współczynnik zmiany skali równa się 0,999923 w południku osiowym.

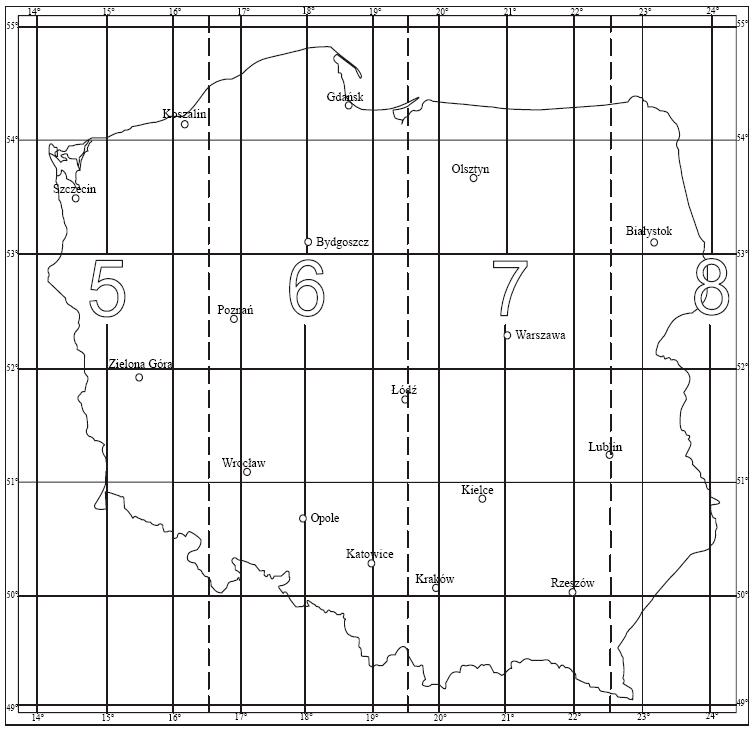
Początkiem układu współrzędnych w danym pasie odwzorowania jest punkt przecięcia się obrazu południka osiowego z obrazem równika. Przy określaniu współrzędnych -  współrzędna x pozostaje nie zmieniona, a do współrzędnej y w zależności od południka osiowego dodaje się np. 5 500 000 m przy południku Lo = 15°, Pierwsza cyfra współrzędnej y oznacza numer pasa odwzorowania.

Najważniejsze cechy:

• elipsoida GRS-80

• odwzorowanie Gaussa-Krügera

• cztery 3-stopniowe pasy odwzorowawcze dla południków 15°, 18°, 21°, 24°

• skala m0 = 0.999923,

• X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m

• obowiązuje od 8.08.2000 r

• dla mapy zasadniczej

Układ ten realizuje kompromis w rozłożeniu zniekształceń liniowych; od -7,7 cm/km na południku środkowym strefy do maksymalnie około +7 cm/km na brzegu strefy.

Układ współrzędnych 1992 (2000 r)

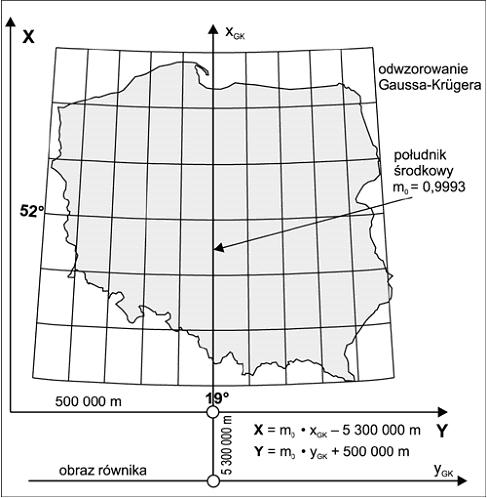
Dla map topograficznych w skali 1:10 000 i mniejszych stosuje się jeden układ dla całego kraju"1992/19" (rys. poniżej ), w systemie GRS 80.

Najważniejsze cechy:

• elipsoida: GRS-80

• odwzorowanie: Gaussa-Krügera

• jeden pas odwzorowawczy dla całej Polski L0 = 19°

• skala m0 = 0.9993,

• X = x - 5 300 000 m, Y = y + 500 000 m

• obowiązuje od 8.08.2000 r

• dla map w skalach 1:10 000 i mniejszych

Dla wyznaczania wysokości w systemie odniesień przestrzennych "1992" stosuje się system wysokości normalnych "Kronsztad 86", w którym zostały określone wysokości punktów podstawowej i szczegółowej osnowy geodezyjnej kraju.

Ze względu na znaczne zniekształcenia liniowe układ nie jest rekomendowany do wielkoskalowych opracowań kartograficznych.

Układ współrzędnych GUGIK 80 (1980 r)

Najważniejsze cechy:

• elipsoida: Krasowskiego

• punkt przyłożenia: Pułkowo (B = 59°46'18.55'', L = 30°19'42.09'')

• azymut orientacji: Pułkowo - Bugry ( A = 121°40'38.79'')

• odwzorowanie quasi-stereograficzne (Roussilhe'a)

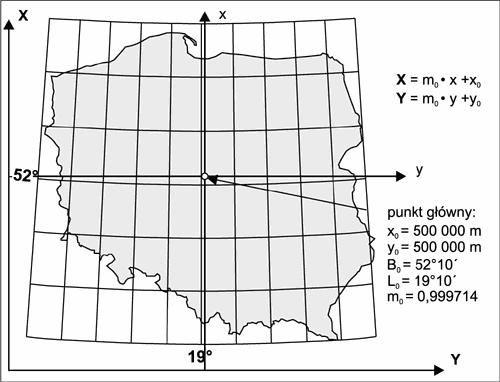
• punkt główny: B = 52°10?, L = 19°10?;

• m0 = 3499/3500, r0 = 215 km

• X0 = 500 000, Y0 = 500 000

Układ współrzędnych 1965 (1965 r)

Układ współrzędnych "1965" wprowadzony został do opracowań kartograficznych przeznaczonych dla potrzeb gospodarczych w roku 1968

Rozporządzeniem Rady Ministrów z dnia 8 sierpnia 2000 r. w sprawie państwowego systemu odniesień przestrzennych układ "1965", oraz lokalne układy współrzędnych mogą być stosowane do dnia 31 grudnia 2009 r.

Najważniejsze cechy

• 
  elipsoida: Krasowskiego

• punkt przyłożenia:  Pułkowo (B = 59°46'18.55'', L = 30°19'42.09'')

• azymut orientacji: Pułkowo - Bugry (A = 121°40'38.79'')

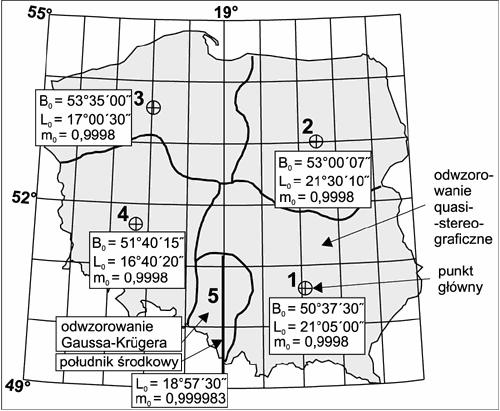
• 5 stref odwzorowawczych:

• w strefach I - IV odwzorowanie quasi-stereograficzne (Roussilhe'a),

• w strefie V odwzorowanie Gaussa-Krügera

• w strefach I - IV skala m0 = 0.9998, r0 = 178.7 km

Mapy sporządzone w państwowym układzie współrzędnych płaskich prostokątnych "1965" nie posiadają siatki kartograficznej. Sporządzone są one w prostokątnym podziale arkuszowym.

układ współrzędnych 1942 (1952 r)

Wprowadzony na podstawie uchwały Prezydium Rządu w 1953 r. w sprawie założenia jednolitej państwowej sieci geodezyjnej i opracowania mapy podstawowej państwa. Uchwała ta zobowiązywała do opracowania i wydania mapy topograficznej w skali 1:25 000 (mapa ta została wykonana dla całego kraju w ciągu 6 lat). Kolejna uchwała Prezydium Rządu, podjęta w 1955 r., zobowiązywała do opracowania mapy topograficznej w skali 1:10 000.

Najważniejsze cehy:

• elipsoida: Krasowskiego

• punkt przyłożenia: Pułkowo (B = 59°46'18.55'', L = 30°19'42.09'')

• azymut orientacji: Pułkowo - Bugry (A = 121°40'38.79'')

• odwzorowanie: Gaussa-Krügera

• dwa 6-stopniowe pasy odwzorowawcze dla południków 15°, 21°

• skala m0 = 1

• X = x, Y = y + (3 500 000, 4 500 000) m

• cztery 3-stopniowe pasy odwzorowawcze dla południków środkowych 15°, 18°, 21°, 24°

• X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m

Przy pomiarach wysokościowych przyjmujemy geoidę Kronsztadzką (teoretyczny poziom Morza Bałtyckiego w Kronsztadzie).

W państwowym układzie współrzędnych płaskich prostokątnych "1942" opracowane zostały mapy topograficzne w skalach 1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:500 000.

Mapy te sporządzone są w odwzorowaniu Gaussa-Krügera. Jest to równokątne poprzeczne odwzorowanie elipsoidy obrotowej na pobocznice walca, przy czym środkowy południk obszaru, zwany też południkiem osiowym, odtwarza się wiernie.

Mapy topograficzne sporządzone w układzie współrzędnych płaskich prostokątnych 1942 mają siatkę kartograficzną i siatkę kilometrową. Arkusze map topograficznych są sporządzane w podziale na sekcje trapezowo-elipsoidalne, przy czym linie podziału pokrywają się z obrazami równoleżników i południków.

Układ współrzędnych Borowa Góra (1920 r)

Opracowany przez Wojskowy Instytut Geograficzny (WIG) w 1936 roku. Obowiązywał do lat 50-tych, do momentu wprowadzenia układu "1942".

 Najważniejsze cechy:

• elipsoida: Bessela

• punkt przyłożenia: Borowa Góra (B = 52°28'32.85'', L = 21°02'12.12'')

• azymut orientacji: Borowa Góra - Modlin (A = 261°53'15.90'')

• odwzorowanie: Roussilhe'a

• skala m0 = 1

• pięć 2-stopniowych pasów odwzorowawczych dla południków: 17° , 19° , 21° ,23° ,25°

• X = x - 5 280 000 m, Y = y + 90 000 m

Modyfikacja odwzorowania z 1920 r

• cztery 3-stopniowe pasy odwzorowawcze dla południków środkowych 15°, 18°, 21°, 24°

• skala m0 = 0.999935

• X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m

• od roku 1949 skala m0 = 1

Wysokości dynamiczne pkt P otrzymujemy dzieląc ujemną wartość różnicy potencjału W_P w pkt P i W_O na geoidzie przez wartość przyspieszenia normalnego na szerokości B=45⁰

H^d_P =(-W_P-W_O)/γ₀⁴⁵

Wykorzystuje się do wyrażenia innych poprawek w innych systemach wysokości.

Wys. dynam. i popr. dynam. są wyznaczane ściśle na podstawie pomierzonych różnic wysokości i przyspieszenia siły ciężkości. Poprawki dynamiczne nie mają żadnej interpretacji geometrycznej. Bardzo ważną właściwością tych wysokości jest to, że pkt. położone na tej samej powierzchni ekwipotencjalnej mają taką samą wys. dynam. System wys. dynam. nie uwzględnia nierówności powierzchni ekwipotencjalnych

Zastosowanie: technika, budownictwo wodne, projekty na bardzo dużych obszarach (gdzie wymagana jest duża dokładność projektowania spadków)

SYSTEMY WYSOKOŚCI

Wysokości otometryczne jest to odległość pkt. fizycznej pow. Ziemi od geoidy mierzona wzdłuż linii pionu (posiada interpretację geometryczną ).

Wys. ortometryczna.

H=C/g, gdzie C=(W_O-W_P)

C - liczba wyrażająca pracę w polu potencjalnym;

g - przeciętna wartość przyspieszenia siły ciężkości wzdłuż linii pionu.

Wysokość normalna Mołodeńskiego:

Wysokość geometryczna telluroidy (odległość telluroidy od elipsoidy)

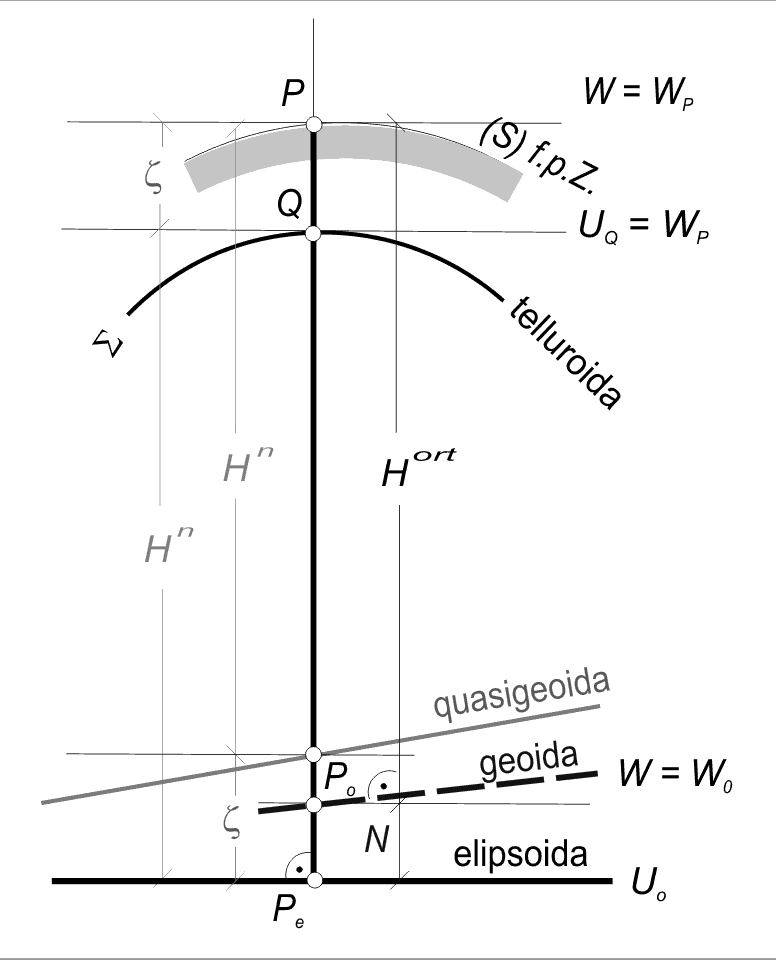
Telluroida (podejście wprowadzone przez Hirvonena) to pewien obraz (przybliżenie) fizycznej powierzchni Ziemi, gdzie dla dwóch punktów na linii pionu pola normalnego (lub normalnej) potencjał normalny w punkcie Q jest taki sam jak potencjał rzeczywisty w punkcie P

1. Wysokości normalne nie maja jasnej interpretacji geometrycznej.

Wyrażają one co prawda odległości pomiędzy geoida i telluroida lub quasigeoida i punktem na fizycznej powierzchni Ziemi, ale zarówno qusigeoida jak i telluroida to powierzchnie `wtórne' w stosunku do wysokości normalnych (nie można ich zdefiniować bez znajomości wysokości normalnych!!!).

2. Quasigeoida nie jest powierzchnia ekwipotencjalna potencjału normalnego, a wiec nie można jej traktować jako powierzchni odniesienia wysokości normalnych w takim samym sensie jak traktuje sie geoide dla wysokości ortometrycznych! Ponadto quasigeoida jest

powierzchnia nieciągła (teoretycznie może leżeć na „dwóch poziomach” dla tych samych współrzędnych np. w przypadku urwiska; taka sytuacja w przypadku geoidy nigdy nie może mieć miejsca!!!).

3. Wysokości i poprawki normalne wyznacza sie bez jakichkolwiek założeń co do rozkładu gęstości warstw przypowierzchniowych skorupy ziemskiej.

4.Punkty leżące na tej samej powierzchni ekwipotencjalnej maja różne

wysokości normalne.

5. Wysokości normalne nadają się do rozwiązywania zagadnień związanych z wyznaczaniem figury Ziemi wg koncepcji Mołodenskiego.

6. Na terenach nizinnych i płaskich różnice wysokości normalnych i ortometrycznych są niewielkie (w Polsce wahają się od 0cm na północy do kilku centymetrów w Tatrach).

7. System wysokości normalnych jest obowiązującym systemem wysokości w Polsce!

Określenie wysokości

Problem określenia wysokości jest odrębnym problemem, wymagającym znajomości odstępów geoidy od elipsoidy WGS84 w danym rejonie. Dokładna mapa takich odstępów zwana mapą geoidy została dla obszaru Polski opracowana w Centrum Badań Kosmicznych PAN przez prof. Adama Łyszkowicza .

Posiadając mapę geoidy (w zapisie cyfrowym) można określić odstęp geoidy w dowolnym, o znanych współrzędnych punkcie z dokładnością lepszą od 5 cm. Wówczas:
H = h + N,
lub
h = H - N,

gdzie:
H - wysokość nad elipsoidą WGS84,
H - wysokość określana jako wysokość nad powierzchnią morza.

Na obszarze Polski odstępy elipsoidy satelitarnej WGS84 od geoidy sięgają od 26 m do 43 m.

---