FALOWA NATURA ŚWIATŁA

• Aby uwzględnić wpływ, jaki ma falowa natura światła na zjawiska, które wyjaśnialiśmy dotąd na bazie optyki geometrycznej, musimy poznać mechanizm promieniowania fal przez źródła i ich detekcji przez odbiorniki.

• Termiczne źródła światła nie wysyłają energii w sposób ciągły, lecz skwantowany. Pobudzenie atomu poprzez pochłonięcie energii termicznej
a następnie oddanie tej energii jako wypromieniowywanej fali elektromagnetycznej (w postaci fotonu) o częstotliwości (średniej)
, zgodnie z wzorem Einsteina:

(
- stała Plancka)

odbywa się w skończonym czasie. Takie procesy pochłaniania i emisji zachodzą wielokrotnie i w rezultacie każdy atom promieniuje ciąg niezależnych fal elementarnych, tłumionych w czasie emisji.

FALOWA NATURA ŚWIATŁA - c.d.

• Zjawisko emisji spontanicznej ma charakter przestrzenny, a wektory natężenia pola elektrycznego
i magnetycznego
każdej fali elementarnej, jakkolwiek leżą w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali (i są zawsze prostopadłe do siebie!), są zorientowane przypadkowo w przestrzeni względem dowolnej innej fali.

Również odległości w przestrzeni między poszczególnymi falami elementarnymi są przypadkowe, bo zależą od przypadkowych odstępów czasowych między kolejnymi (niezależnymi!) aktami emisji.

DETEKCJA PROMIENIOWANIA

• Częstotliwość promieniowania optycznego jest rzędu 10¹² Hz (pasmo widzialne). Nie istnieją odbiorniki tak „szybkie” (o tak małej stałej czasowej), żeby były w stanie zarejestrować takie zmiany, możemy więc mówić tylko o detekcji średniej gęstości energii
(odbiorniki promieniowania e.-m. są czułe na energię tego promieniowania!) w pewnym czasie
, różnym dla różnych odbiorników, ale dużo większym od okresu drgań fali e.-m.:

Wprowadzając oznaczenie:

(średnia czasowa)

możemy zapisać:

Wektor
nazywany wektorem optycznym i możemy w jego miejsce podstawić zarówno wektor
jak i
(oko ludzkie „widzi”
!)

DETEKCJA PROMIENIOWANIA - c.d.

• Dla uproszczenia przyjmijmy, że w czasie
promieniowanie jest ciągłe i nietłumione. Jeżeli punkt detekcji znajduje się dostatecznie daleko od źródła, falę możemy uważać za płaską i przedstawimy ją w postaci zespolonej:

gdzie
oznacza niezależna od czasu amplitudę zespoloną. Przedstawienie w postaci funkcji zespolonej ma swoje zalety, jeśli chodzi o zagadnienia związane z propagacją fali, ale sens fizyczny ma część rzeczywista
i te wielkość podstawimy do wzoru na średnią gęstość energii:

Po rozwinięciu wyrażenia w nawiasie otrzymamy:

DETEKCJA PROMIENIOWANIA - c.d.²

• Poszczególne człony średniego natężenia są równe:

Podobnie:

Ostatecznie dostaniemy więc:

Wielkość:
nazywamy intensywnością fali i jest ona miarą energii fali w jednym ośrodku (ośrodki mogą się różnić stałą dielektryczną, dlatego nie można porównywać intensywności w dwóch różnych ośrodkach!).

MONOCHROMATYCZNOŚĆ PROMIENIOWANIA

• Fala - to rozchodzące się w przestrzeni, zależne od czasu, zaburzenie.

• Fala monochromatyczna płaska to fala harmoniczna o postaci:

gdzie:
- częstość kołowa fali;
- amplituda zespolona;
- liczba falowa. (Uwaga: ta fala rozchodzi się w kierunku „z”).

Częstotliwość fali:
;

Długość fali:
.

• Jeżeli rozważamy przejście fali przez ustalony punkt przestrzeni
(detekcja!), to można odnieść fazę początkową fali do tego punktu i zapisać:

MONOCHROMATYCZNOŚĆ PROMIENIOWANIA - c.d.

• Każdy atom rozgrzanego ciała promieniuje pewien ciąg fal elementarnych o skończonym czasie emisji. Załóżmy nawet brak ograniczeń na „końcach” takiej fali elementarnej - czyli przyjmijmy, że jest ona ściśle harmoniczna, ale zeruje się poza pewnym obszarem
:

•

dla:

•
dla:

TRANSFORMACJA FOURIERA

• Szereg Fouriera to sposób na przedstawienie dowolnej funkcji periodycznej (o okresie
i częstości
):

w postaci sumy funkcji harmonicznych (albo całki..)

gdzie współczynniki
i
są amplitudami tych funkcji harmonicznych, obliczonymi ze wzorów Eulera-Fouriera:

Parametr
jest dowolną wartością
.

TRANSFORMACJA FOURIERA - c.d.

• Przykład I: Funkcja prostokątna
:

dla:
i
dla:

Transformata tej funkcji:

i ponieważ:

więc:

(oznaczenie: funkcja „sink”:
)

TRANSFORMACJA FOURIERA - c.d.²

• Przykład I: Funkcja prostokątna, periodyczna, o ograniczonej długości:

MONOCHROMATYCZNOŚĆ PROMIENIOWANIA - c.d.²

• Zgodnie z przekształceniem Fouriera możemy naszą „paczkę falową” przedstawić jako nieskończoną sumę funkcji harmonicznych (monochromatycznych!):

gdzie
jest amplitudą składowej fali harmonicznej:

Obliczenia szczegółowe doprowadzą do wzoru:

gdzie:
.

MONOCHROMATYCZNOŚĆ PROMIENIOWANIA - c.d.³

• Detektory reagują na intensywność promieniowania, która będzie wobec tego równa:

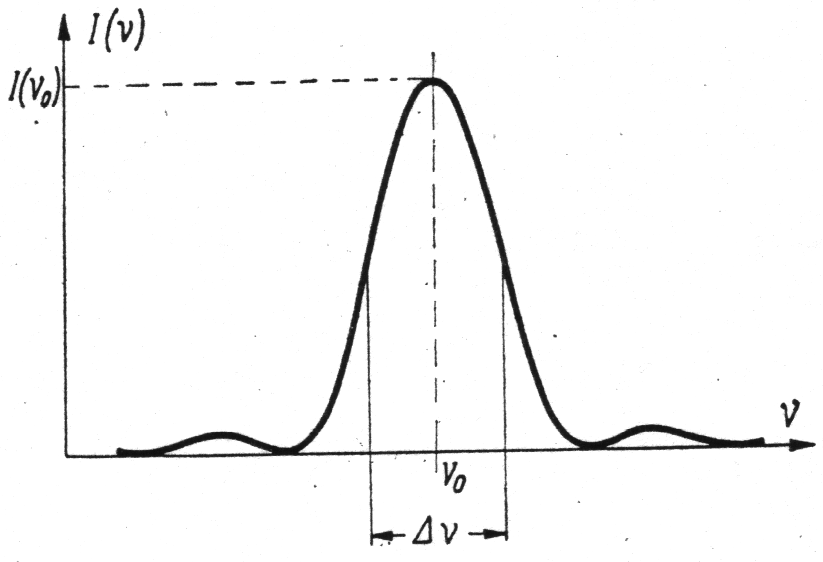
Tak więc fala elementarna, chociaż harmoniczna (o jednej częstości) ale tylko w skończonym obszarze („paczka”), odpowiada tak naprawdę pewnemu przedziałowi widma promieniowań monochromatycznych, któremu odpowiada przedział długości fal:

MONOCHROMATYCZNOŚĆ PROMIENIOWANIA - c.d.⁴

• Funkcja
jest co prawda określona dla
, ale przyjmuje pierwsze wartości zerowe dla:
a dla większych wartości
jej kolejne maksima są dużo mniejsze od głównego, więc możemy z dobrym przybliżeniem przyjąć za szerokość funkcji intensywności wielkość:

• Podobne zależności można by wyprowadzić dla fali tłumionej w czasie emisji. Wniosek: Promieniowanie atomu z uwagi na skończone długości (czasy trwania emisji) fali elementarnej nie jest nigdy promieniowaniem monochromatycznym. Im krótszy jest przedział czasu
, w którym emitowana jest fala elementarna, tym szerszy jest przedział częstości emitowanego widma.

• Na poszerzenie przedziału widmowa ma wpływ też zjawisko Dopplera, ponieważ atomy w czasie emisji przemieszczają się.

EFEKT DOPPLERA

• Efekt ten polega na zmianie częstości odbieranej fali, jeśli źródło fali porusza się względem obserwatora.

Po raz pierwszy efekt został naukowo zaobserwowany przez Christiana Andreasa Dopplera w 1845 roku. Poprosił on grupę muzyków, aby wsiedli do pociągu i grali jeden ton. Słuchał go i zaobserwował, że dźwięk instrumentów staje się wyższy, kiedy pociąg zbliża się do niego. Gdy źródło muzyki się oddala, jego ton staje się niższy. Zmiana wysokości dźwięku była dokładnie taka, jak wyliczył uprzednio Doppler.

EFEKT DOPPLERA - c.d.

• Jeżeli źródło zbliża się do obserwatora z prędkością
:

• Jeżeli obserwator zbliża się do źródła z prędkością
:

• Klasyczny efekt Dopplera:

• Relatywistyczny efekt Dopplera:

ODBICIE I ZAŁAMANIE PŁASKIEJ FALI MONOCHROMATYCZNEJ

• Niech
będzie płaszczyzną dzielącą dwa ośrodki o współczynnikach załamania
i
. W pierwszym ośrodku rozchodzi się fala płaska w kierunku wyznaczonym przez wersor
.

Posługując się opisem fal płaskich, z warunków równości faz obu fal można wyprowadzić prawo załamania (i odbicia) dla fal płaskich:

ODBICIE I ZAŁAMANIE PŁASKIEJ FALI MONOCHROMATYCZNEJ - c.d.

• Prawa załamania (i odbicia) ustalają tylko kierunki rozchodzenia się fal. Należałoby natomiast uzyskać ilościowe związki między tymi falami - to jest podać związki między amplitudami i energią tych fal.

Oznaczenia:

,
,
- wersory fali: padającej, załamanej, odbitej;

- zespolona amplituda wektora elektrycznego fali padającej; (wektor ten leży w płaszczyźnie prostopadłej do
).

ODBICIE I ZAŁAMANIE PŁASKIEJ FALI MONOCHROMATYCZNEJ - c.d.²

• Związki między wektorami fal dla obydwu przekrojów (w płaszczyźnie padania
i prostopadle do niej
) są nazywane wzorami Fresnela:

Uzupełnieniem powyższych wzorów są oczywiście prawa załamania.

WZORY FRESNELA

• Dla prostopadłego padania fali na granicę ośrodków (
,
) otrzymamy prostsze formuły na poszczególne składowe fal:

gdzie:
; (zanika różnica między składowymi, więc można podać natężeniowe współczynniki transmisji i odbicia).

• Współczynniki przy poszczególnych składowych zarówno dokładnych formuł Fresnela jak i tych dla prostopadłego padania są rzeczywiste (pomijając przypadek całkowitego wewnętrznego odbicia) i mogą przyjmować wartości dodatnie i ujemne.

• Te same znaki oznaczają te same zwroty poszczególnych wektorów - mówimy, że wektory są (zgodne) w fazie;

• Przeciwne znaki oznaczają, że wektory są niezgodnych zwrotów - mówimy o skoku fazy o
  ;

WZORY FRESNELA - c.d.

• Dla fali przechodzącej niezależnie od wartości względnego współczynnika załamania
i kąta padania znak składowych wektora fali przechodzącej jest ten sam, co fali padającej i skok fazy nie następuje. Dla fali odbitej mogą zdarzyć się skoki fazy (w zależności od
i kątów padania).

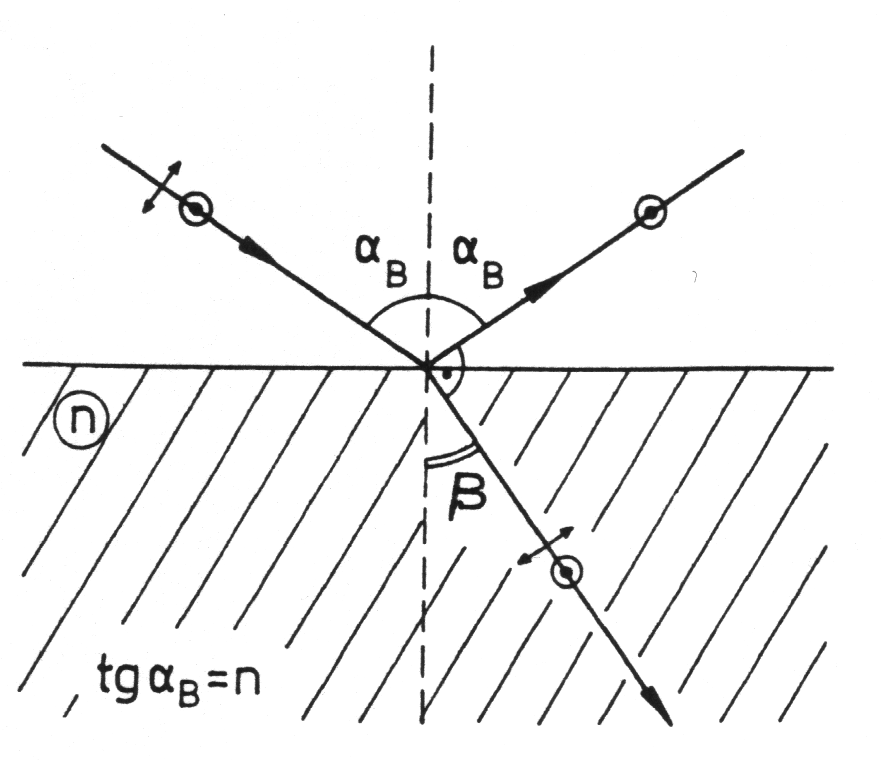
• Dla
jest:
. Oznacza to, że fala odbita nie ma składowej w płaszczyźnie padania. Kąt padania, dla którego spełniony jest ten warunek, nazywany jest kątem Brewstera
. Można pokazać, że wtedy spełniony jest warunek:

ZALEŻNOŚCI ENERGETYCZNE

• Energię poszczególnych fal opisują kwadraty amplitud wektorów świetlnych (pomnożone przez czynnik
). Ze względu na istnienie poszczególnych składowych (prostopadłej i równoległej) fali odbitej i załamanej, musimy „podzielić” gęstość energii fali padającej:

i

• Współczynnik odbicia
definiujemy jako:

• Współczynnik przepuszczania
definiujemy jako:

ZALEŻNOŚCI ENERGETYCZNE - c.d.

• Współczynniki odbicia i przepuszczania można przedstawić w rozbiciu na składowe:

gdzie poszczególne składowe spełniają oczywiście prawa Fresnela.

• Z praw zachowania energii wynika oczywiście, że:

• Dla światła naturalnego (niespolaryzowanego), dla którego każde położenie wektora optycznego fali opadającej jest jednakowo prawdopodobne, możemy obliczyć wartości współczynników: odbicia i przepuszczania jako średnie wartości dla wszystkich kątów
:

i

ZALEŻNOŚCI ENERGETYCZNE - c.d.²

• Po obliczeniu odpowiednich całek, otrzymamy:

i

• Światło naturalne doznaje więc częściowej polaryzacji poprzez załamanie i odbicie. Stopień polaryzacji można wyznaczyć ze wzoru:

Maksymalny stopień polaryzacji przy odbiciu zachodzi dla kąta Brewstera - fala odbita jest wtedy całkowicie spolaryzowana liniowo.

• Dla fali padającej prostopadle do granicy ośrodków, zależności są prostsze:

ZALEŻNOŚCI ENERGETYCZNE - c.d.³

• Wykres zależności wartości
i
w funkcji kąta padania dla przykładowego

CAŁKOWITE ODBICIE

• Jeżeli fala wychodzi z ośrodka o większym współczynniku załamania do ośrodka o mniejszym współczynniku załamania (
), to istnieje wtedy graniczny kąt padania
, dla którego:

• Wykorzystując wzory Fresnela, można pokazać, że energia fali odbitej jest równa energii fali padającej i fala pozostaje w pierwszym ośrodku - natomiast obie składowe tej fali doznają skoków fazy, które powodują, że w szczególności światło spolaryzowane liniowo przy całkowitym odbiciu staje się spolaryzowane eliptycznie.

25

---