Nr ćwicz. 308	Data 27.04.2011		Wydział: Technologii Chemicznej Kierunek: Technologia Chemiczna	Semestr II	Grupa 1.5
Prowadzący: dr J.Barańska			Przygotowanie:	Wykonanie:	Ocena:

Temat: Wyznaczanie współczynnika załamania światła za pomocą refraktometru Abbego.

1. Prawo załamania światła (Snella).

Promień świetlny na granicy dwóch ośrodków (optycznie gętszego i optycznie rzadszego) ulega załamaniu tworząc w ośrodku gęstszym mniejszy kąt z normalną do powierzchni niż w ośrodku rzadszym. Przy tym zja-wisku wyróżniamy kąt padania oraz kąt załamania promienia świetlnego. Stosunek sinusów obu tych kątów jest wielkością stałą dla danej pary ośrodków i danej długości fali świetlnej.

n1, n2 bezwzględne współczynniki załamania światła w ośrodkach.

Bezwzględny współczynnik załamania światła określony jest stosunkiem prędkości światła w próżni c do prędkości światła w danym ośrodku v.

Ze względu na to, że prędkość światła jest największa w próżni, bezwzględny współczynnik załamania światła jest dla wszystkich ośrodków materialnych większy od jedności.

Załamanie światła na granicy dwóch ośrodków materialnych jest określone ich względnym współczynnikiem załamania

W praktyce często przyjmuje się, że powietrze ma współczynnik załamania bardzo bliski wartości dla próżni (n=1).

2. Zależność współczynnika załamania światła od długości fali.

Ponieważ kąt w między promieniem świetlnym w drugim ośrodku a normalną do granicy ośrodków zależy od długości fali, zatem również wartość współczynnika załamania zależy od długości fali. Z tego względu zała-manie w odróżnieniu od odbicia moze być wykorzystane do rozłożenia wiązki światła na składowe o róznych długościach fali ( w tym ćwiczeniu efekt niepożądany).

3. Całkowite wewnętrzne odbicie.

Promienie biegnące z ośrodka optycznie gęstszego do ośrodka optycznie rzadszego odchylają się od normalnej tym bardziej, im większy jest kąt padania a. Dla pewnej jego wartości promień świetlny nie wchodzi nawet do drugiego ośrodka "ślizgając się" po powierzchni granicznej. Co zgodnie z prawem Snella daje:

Przy dalszym zwiększaniu wartości kąta padania promień zaczyna odbijać się od powierzchni granicznej wra-cając do ośrodka pierwszego.

4. Procent energii odbitej i załamanej na granicy dwóch ośrodków.

W większości przypadków mamy do czynienia z dwoma zjawiskami naraz: odbiciem i załamaniem światła na granicy dwóch ośrodków. Pozostaje pytanie jaki procent energii niosą dalej fale odbita i załamana. Równania Maxwella pozwalają obliczyć w jaki sposób energia niesiona przez falę dzieli się pomiędzy nimi. Najlepiej widać to na przykładzie powietrze--szkło:

wiązka z powietrza do szkła

wiązka ze szkła do powietrza

5. Dyspersja światła.

Dyspersja to zjawisko polegające na rozszczepieniu światła białego przy przejściu przez pryzmat. Jest ono w tym ćwiczeniu niepożądane. Stosuje się więc układ pryzmatów, z których każdy odchyla światło w przeciwną stronę, ponieważ sa obrócone względem siebie o 180°. W sumie efekty ich działania się znoszą się. W refra-ktometrze układ ten służy do kompensacji dyspersji wywołanej przez badaną ciecz.

6. Refraktometr Abbego i zasada jego działania.

Zasadniczą częścią refraktometru Abbego są dwa prostokątne pryzmaty za szkła flintowanego, posiadające duży współczynnik załamania. Jeden z pryzmatów można odchylać obracając go wokół osi. Po odchyleniu na jego powierzchni na jego powierzchni przeciwprostokątnej umieszcza się kilka kropel badanej cieczy, która po dociśnięciu pryzmatów tworzy cinką płaskorównoległą warstwę. Należy tak ustawić pryzmaty, by część światła padała na ciecz pod kątem granicznym. Przy takim biegu promienia świetlnego w polu widzenia lunetki zauważymy obszar jasny i ciemny. Położenie granicy między tymi obszarami zależy od wartości współczynnika załamania cieczy. Granica ta jest naprowadzana na środek pola widzenia przez obrót pryzmatów za pomocą pokrętła sprzężonego z podziałką, z której odczytuje się wartość współczynnika załamania. By uniknąć niepożądanych efektów dyspersji wprowadzonej przez ciecz stosuje sie układ opisany punkt wyżej. Spotyka się też kryształy anizotropowe.

7. Kryształy anizotropowe.

Mają one nieliniowe właściwości przewodzenia światła w róznych kierunkach. Zachodzi tu zjawisko podwójnego załamania.

Pomiary:

Zależność współczynnika załamania od stężenia roztworu w temperaturze 24^oC.

δn=0,001

Cp roztworu gliceryny [%]	współczynnik załamania cieczy - n
H2O	1,33
10	1,34
30	1,37
50	1,39
70	1,42
100	1,46
x	1,373

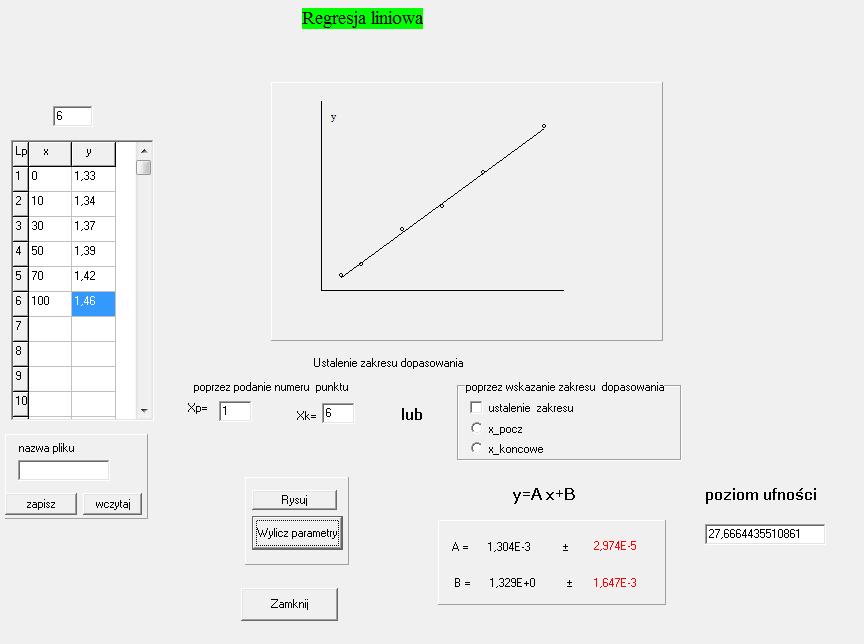
Obliczenie stężenia roztworu X za pomocą regresji liniowej:

Zmiana wartości współczynnika załamania gliceryny od temperatury.

1. Podgrzewanie

temperatura [^oC]	współczynnik załamania cieczy
29,5	1,422
36	1,420
53	1,419
58	1,416
63	1,415
67	1,414
70	1,413
74	1,412

2. Chłodzenie

temperatura [^oC]	współczynnik załamania cieczy
25,5	1,423
27	1,422
35	1,421
37	1,420
42	1,419
45	1,418
50	1,417
54	1,416
59	1,415
68	1,413
74	1,412

Wartości
i
są dane (odczytać je można z przyrządów mierniczych. Wartość
, ponieważ wartości stężeń C również są dane. Nie ma zatem potrzeby wykonywania obliczeń w celu ustalenia błędu.

Zgodnie z poleceniem ćwiczenia nanosimy słupki błędów na powyższe wykresy zależności.

Wnioski

Refraktometr Abbego jest bardzo dokładnym przyrządem, jeśli chodzi o pomiar współczynnika załamania światła w określonej temperaturze.

Błąd pomiaru współczynnika załamania nie zależy jedynie od skali refraktometru - przy niewłaściwym pokryciu pryzmatu roztworem granica między dwoma ośrodkami materialnymi staje się nieostra, przez co trudno ustalić dokładną wartość współczynnika załamania. Istotny jest również wpływ dyspersji światła na wynik pomiaru - należy zastosować odpowiedni układ kompensujący ten efekt.

Gliceryna jest substancją o wysokiej wartości współczynnika załamania wobec próżni/powietrza - n dla czystej gliceryny w warunkach normalnych wynosi 1,469.

---