Funkcje trygonometryczne (to się tylko tak ,,strasznie” nazywa) powrót

1. Pojęcia podstawowe

Problem 1 : Skąd wzięły się funkcje trygonometryczne ?

Odp : Jakiś ,,pacjent” wymyślił, że gdy podzielimy dwa boki trójkąta prostokątnego to taką matmę nazwiemy

funkcją trygonometryczną. Ponieważ w trójkącie prostokątnym jest trzy boki, to można z nich ułożyć aż sześć

różnych dzieleń dwóch boków (mogłoby więc być 6 różnych funkcji trygonometrycznych). Na nasze ,,szczęście” jest ich cztery. Trzeba się tylko umówić : jakie dzielenie dwóch boków otrzyma jedną z tych popapranych nazw - sinus=sin, kosinus=cos, tangens=tg, kotangens=ctg.

Krócej : funkcje trygonometryczne bierzemy z głowy i trójkąta prostokątnego.................................cofnij

Problem 2 : Jak otrzymać jakąś funkcję trygonometryczną ?

Odp : 1. Trzeba widzieć trójkąt prostokątny z oznaczonymi bokami i kątami. (patrz)

2. Umówić się jak wybierać dwa boki trójkąta (do dzielenia) aby móc je nazwać (sin, cos, tg, ctg).

Umowa : boki będziemy wybierać z rysunku patrząc na ich położenie względem kątów ostrych trójkąta prostokątnego. Ponieważ kątów takich jest dwa, musiały być na rysunku oznaczone.

Funkcje będą omówione w kolejności ,,łatwości” ich zapamiętywania............................................... cofnij

I. sinus (wersja ,,moja”) (a tu znajdziesz wersję szkolną)

Aby mieć sinusa kąta ostrego trzeba z trójkąta prostokątnego wziąć : pod kreskę ułamkową bok najdłuższy, a nad kreskę ułamkową bok który nie dotyka branego pod uwagę kąta ostrego.

W trójkącie prostokątnym możemy znaleźć dwa sinusy - bo są dwa kąty ostre α i β .

1. Znajdziemy sinus kąta α (skrót to sinα ).

2. Teraz sinβ .

Zapamiętać : do sinusa na ,,górę” bok który nie dotyka kąta; na ,,dół” najdłuższy..................................... cofnij

II. kosinus (wersja ,,moja”) (a tu znajdziesz wersję szkolną)

Aby mieć kosinusa kąta ostrego trzeba z trójkąta prostokątnego wziąć : pod kreskę ułamkową bok najdłuższy, a nad kreskę ułamkową bok który dotyka kąta ostrego używanego w zapisie.

W trójkącie prostokątnym możemy znaleźć dwa kosinusy - bo są dwa kąty ostre α i β .

1. Znajdziemy kosinus kąta α (skrót to cosα ).

2. Teraz cosβ .

Zapamiętać : do kosinusa na ,,górę” bok który dotyka kąta; na ,,dół” najdłuższy............................. cofnij

Podsumowanie - do każdego sinusa i kosinusa na ,,dół” bok najdłuższy; na ,,górę” do sinusa ten co nie dotyka kąta; na ,,górę” do kosinusa ten co dotyka kąta.

Problem 3 : Do poniższego rysunku napisz równania funkcji sinus i kosinus obu kątów ostrych :

Odp : sinα =
(u nie dotyka α ; n jest najdłuższy) sinβ =
( z nie dotyka β ; n jest najdłuższy)...................... cofnij

.........cosα =
( z dotyka α ; n jest najdłuższy) cosβ =
(u dotyka β ; n jest najdłuższy)

Z1. Napisz równania funkcji trygonometrycznych (sinus i kosinus)do rysunku :

zajrzyj

III. tangens (wersja ,,moja”) (a tu znajdziesz wersję szkolną)

Uwaga : do żadnego tangensa ani kotangensa nie możemy brać boku najdłuższego.

Aby mieć tangensa kąta ostrego trzeba z trójkąta prostokątnego wziąć : nad kreskę ułamkową bok który nie dotyka kąta (ten sam co do sinusa), a pod kreskę został nam już tylko jeden (bo najdłuższego nie możemy wziąć).

W trójkącie prostokątnym możemy znaleźć dwa tangensy - bo są dwa kąty ostre α i β . Ustalamy tangensy do rysunku z problemu 2.

1. Znajdziemy tangensa kąta α (skrót to tgα ).......................................................................................... cofnij

2. Teraz tgβ .

Zapamiętać : do tangensa na ,,górę” bok który nie dotyka kąta (tak jak do sinusa); na ,,dół” nie najdłuższy.

IV. kotangens (wersja ,,moja”) (a tu znajdziesz wersję szkolną)

Aby mieć kotangensa kąta ostrego trzeba z trójkąta prostokątnego wziąć : nad kreskę ułamkową bok który dotyka kąta (ten sam co do kosinusa), a pod kreskę został nam już tylko jeden (bo najdłuższego nie możemy wziąć).

W trójkącie prostokątnym możemy znaleźć dwa kotangensy - bo są dwa kąty ostre α i β . Ustalamy kotangensy do rysunku z problemu 2.

1. Znajdziemy kotangens kąta α (skrót to ctg α )................................................................................ cofnij

2. Teraz ctg β .

Zapamiętać : do kotangensa na ,,górę” bok który dotyka kąta (tak jak do kosinusa); na ,,dół” nie najdłuższy.

Podsumowanie - do żadnego tangensa ani kotangensa nie bierzemy boku najdłuższego; na ,,górę” do tangensa ten co nie dotyka kąta; na ,,górę” do kotangensa ten co dotyka kąta.

Problem 4 : Do rysunku z problemu 3 napisz równania funkcji tangens i kotangens obu kątów ostrych.

Odp : tg α =
(u nie dotyka α ; z nie jest najdłuższy)..tgβ =
(z nie dotyka β ; u nie jest najdłuższy)

..........ctg α =
(z dotyka α ; u nie jest najdłuższy) ctgβ =
(u dotyka β ; z nie jest najdłuższy)..

Z2. Napisz wszystkie równania funkcji trygonometrycznych kątów ostrych do poniższego rysunku....................... cofnij

zajrzyj

Szkolne definicje funkcji trygonometrycznych.

1. Sinusem kąta ostrego, w trójkącie prostokątnym, nazywamy stosunek przyprostokątnej przeciwległej temu kątowi do przeciwprostokątnej.

2. Kosinusem kąta ostrego, w trójkącie prostokątnym, nazywamy stosunek przyprostokątnej przyległej kątowi do przeciwprostokątnej.

3. Tangensem kąta ostrego, w trójkącie prostokątnym, nazywamy stosunek przyprostokątnej przeciwległej temu kątowi do drugiej przyprostokątnej.

4. Kotangensem kąta ostrego, w trójkącie prostokątnym, nazywamy stosunek przyprostokątnej przyległej kątowi do drugiej przyprostokątnej.

6. Tabelka (wartości funkcji trygonometrycznych kątów 30⁰; 45⁰; 60⁰)

Problem 5 : Skąd te kąty ?

Odp : Z trójkątów prostokątnych które powstają z przecięcia na ,,pół” trójkąta równobocznego (30⁰; 60⁰) lub kwadratu (45⁰). Albo z ekierek (tych plastikowych).

Problem 6 : Jak zapamiętać tę cholerną tabelkę ?

Odp : 1. Ponieważ do każdego sinusa i kosinusa na ,,dół” bierzemy to samo, to w tabelce wystarczy znać tylko jeden ,,dół” dla tych funkcji (2).

2. Ponieważ do żadnego tangensa i kotangensa nie bierzemy tego co na ,,dół” sinusa i kosinusa, to w tabelce dla tg i ctg nie będzie nigdzie 2.

3. Ponieważ sinus traktowany ma być jako najłatwiejszy, to w tabelce dla niego u ,,góry” będzie 1; 2; 3 (ale pod pierwiastkami; a
= 1). Dla kosinusa będą te liczby wpisane w odwrotnej kolejności.

4. Środkowa wartość dla tg i ctg jest najłatwiejsza to 1. A we wszystkich pozostałych jest
; ale podzielony przez trzy w pierwszej rubryce tg i w trzeciej ctg.

A oto jak wygląda cała tabelka :

a	30^0	45^0	60^0
sina
cosa
tga		1
ctga		1

7. Zastosowanie funkcji w zadaniach

Problem 7 : Po co nam te funkcje ?

Odp : ............................(to miejsce było na Twoją odpowiedź; chyba wolałbym jej nie znać).

Oficjalnie po to aby wyznaczać brakujące długości lub kąty w zadaniach z matmy (jak to robić przedstawię na przykładach).

Problem 8 : Rozwiąż równanie : a) sin 30⁰ =
; b) ctg 45⁰ =
; c) tg 60⁰ =
.

Ad. a) zamiast sin 30⁰ wpisujemy do równania ,,zapamiętaną” wartość z tabelki (czyli
); mamy :

=
..(teraz mnożenie na ,,krzyż”)

2∙ x = 1 ∙ 6

2x = 6│:2

x = 3..(skończone)

Ad. b) zamiast ctg 45⁰ wpisujemy ,,zapamiętane” 1; mamy :

1 =

1∙ c = 4

c = 4

Ad. c) zamiast tg 60⁰ wpisać
; mamy :

=

1∙ d = 5∙

d = 5

Z3. Rozwiąż równania : a) cos 60⁰ =
; b) sin 45⁰ =
; c) tg 30⁰ =
.

zajrzyj

Problem 9 : Zadania w których można skorzystać z funkcji trygonometrycznych.

1. Wyznacz długości wszystkich boków trójkąta z rysunku :

Rozwiązanie.

Temat podpowiada aby napisać równanie z trygonometrią, np:.............................................................. cofnij

sin 30⁰ =
..(jest w nim tylko jedna niewiadoma y, możemy go rozwiązać; patrz problem 8)

..(mnożenie na krzyż)

2∙y = 1∙8

2y = 8│:2

y = 4..(a teraz możemy z Pitagorasa; ale lepiej dalej z trygonometrycznych)

cos 30⁰ =

2∙x = 8∙

2x = 8
│:2

x = 4

Odp : Długości szukanych boków to : 4 i 4
..................................................................................cofnij

Z4. Oblicz pole prostokąta w którym przekątna o długości 10 m tworzy z jednym bokiem kąt 60⁰.

zajrzyj

Z5. Wyznacz pole i obwód trapezu równoramiennego w którym podstawy to 8 i 12, a jego kąt ostry to 30⁰.

zajrzyj

Z6. W trójkącie równoramiennym kąt między ramionami to 120⁰, a ramię to 20 cm. Podaj obwód tego trójkąta.

zajrzyj

8. Zależności między funkcjami trygonometrycznymi

Problem 10 : Po co Ci to ?

Odp : ..............................(miejsce na Twoją)

Oficjalnie po to aby poradzić sobie z problemami jakie trafisz w tym dziale.

Według mnie wcale Ci nie są te zależności potrzebne, bo nauczę Cię jak robić bez nich.

Do szkoły trzeba na ściągę wpisać :

1. sin² α + cos² α = 1..(to tak zwana ,,jedynka trygonometryczna”) Równanie uzależniające od siebie sinusa i kosinusa tego samego kąta.

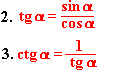
Równanie uzależniające tangensa od sinusa i kosinusa.

Równanie uzależniające kotangensa od tangensa.

Problem 11 : Jak wyznaczyć wartości wszystkich funkcji trygonometrycznych gdy znamy wartość jednej z nich ?

Odp : Nauczyciele chcieliby aby robić to korzystając z powyższych czerwonych równań (jeśli ktoś zechce i ja może to pokażę); można jednak poradzić sobie inaczej (znaczy dużo łatwiej). Patrz poniższe przykłady.

Przykład 1 :Wiedząc, że sin α =
wyznacz wartości pozostałych funkcji trygonometrycznych kąta α .................. cofnij

Zaczynamy od ,,wymyślenia” trójkąta prostokątnego w którym jest kąt ostry α oraz któreś z boków to 5 i 13

(ponieważ takie boki ktoś widział dając nam wartość sinusa α w zadaniu). Wiemy z ,,teorii” , Ώe najdłuższy w tym trójkącie to 13 (na dole w sinusie), a ten co nie dotyka α to 5 (na górze w sinusie). Więc układający zadanie widział trójkąt :

Trzeba wyznaczyć długość boku x (z Pitagorasa), a potem mając wszystkie boki trójkąta napisać wartości wszystkich funkcji jakie ktoś chciał (zgodnie z poznaną ,,teorią” doboru boków). Jedziemy :

x² + 5² = 13²

x² + 25 = 169

x² = 169 - 25

x² = 144

x = 12..(i już możemy wypisywać wszystkie wartości funkcji trygonometrycznych kata α )............................. cofnij

Odp : cos α =
..(13 najdłuższy; 12 dotyka α )

tg α =
..(bez najdłuższego; na górę ten co do sinusa, czyli 5)

ctg α =
..(bez najdłuższego; na górę ten co do kosinusa, czyli 12) skończone

Przykład 2 : Dany jest tg β = 2. Wyznacz wartości pozostałych funkcji trygonometrycznych kąta β .

Zaczynamy od ,,wymyślenia” trójkąta prostokątnego w którym jest kąt ostry β oraz któreś z boków to 2 i 1

(ponieważ takie boki ktoś widział dając nam wartość tg β w zadaniu; u góry w tangensie miał 2, a na dole 1). Wiemy z ,,teorii” , że najdłuższego w tangensie nie było, a na górze był bok który nie dotykał kąta β ; zatem mamy trójkąt :

Trzeba wyznaczyć długość boku x (z Pitagorasa), a potem mając wszystkie boki trójkąta napisać wartości wszystkich funkcji jakie ktoś chciał (zgodnie z poznaną ,,teorią” doboru boków). Jedziemy :....................................... cofnij

1² + 2² = x²

1 + 4 = x²

5 = x²

x² = 5

x =

Odp : sin β =

cos β =

tg β =
.

Z7. Oblicz wartości wszystkich funkcji trygonometrycznych kąta α gdy :

a) cos α =
;

b) ctg α = 3 .

zajrzyj........................................................................................................................................ cofnij

9. Wykresy funkcji trygonometrycznych

Potrzebne są do rozwiązywania równań i nierówności trygonometrycznych.

Wszystkie znajdziesz tutaj.

10. Wzory redukcyjne

Jeśli chcesz poznać wszystkie wzory redukcyjne to otwieraj książkę i ucz się ich.

Ja proponuję poznać je trochę inaczej (czyli sensowniej i łatwiej).

Problem 12 : Po co są wzory redukcyjne ?

Odp : Po to abyśmy mogli wyznaczyć wartość jakiejś funkcji trygonometrycznej ,,dużego” kąta.

Wzorami redukcyjnymi ,,zmniejszymy” taki kąt tak aby był mniejszy (lub równy) od kąta prostego.

Problem 13 : Skąd ,,duży” kąt ?

Odp : Jeśli znasz już wykresy funkcji trygonometrycznych, to wiesz, że istnieją one dla różnych kątów.

Kąty te mierzono na układzie współrzędnych o tak :....................................................................................... cofnij

W związku z tym przyjęto, że kąt odmierzany od dodatniej półosi x przeciwnie do ruchu wskazówek zegara jest dodatni (a zgodnie z ruchem wskazówek jest ujemny). Kątami ujemnymi nie będziemy sobie zawracali głowy - da się bez nich wszystko zrobić, w dalszej części wyjaśnię jak (nikt przecież nie przepada za ujemnymi ,,rzeczami”).

Zapamiętaj : oś pionowa (y) jest osią ,,niebezpieczną” (będę używał tego określenia w kolejnych rozważaniach).

Kąty w poszczególnych ćwiartkach układu współrzędnych to:.................................................................... cofnij

I - od 0⁰ do 90⁰;

II - od 90⁰ do 180⁰;

III - od 180⁰ do 270⁰;

IV - od 270⁰ do 360⁰.

Ponieważ można kąt odmierzać nieskończenie ,,długo” podane wartości dotyczą tylko jednego obrotu na plus

(ale to nam wystarczy).

Kąty z osi pionowej (y) są ,,niebezpieczne”, czyli : 90⁰ i 270⁰.

Wierszyk o znakach funkcji w ćwiartkach układu :

w pierwszej wszystkie (funkcje) są dodatnie,

w drugiej tylko sinus,

w trzeciej tangens i kotangens,

a w czwartej kosinus.

Problem 14 : Stosowanie ,,wzorów redukcyjnych”...................................................................................... cofnij

Ktoś zaraz wytknie mi, że jeszcze wzorów nie było. Spokojna Twoja ......

Ja ich nie znam i żyję. Poważniej - mogę zrobić bez nich wszystkie zadania.

Mam nadzieję, że przytoczone poniżej przykłady wystarczą ścisłym mózgom (przecież jest to problem z programu rozszerzonego, dla innych też jest to do załapania - tak sądzę).

Uwaga : w szkołach chcą aby uczniowie nauczyli się wzorów (nie spotkałem jeszcze takiej w której byłoby inaczej), tutaj dostaniesz trzy zasady dzięki którym można uniknąć nauki tych wzorów.

Zasady te można stosować w dowolnej kolejności, chociaż najlepiej starać się od 1 przez 2 do 3.

Przykład 1 : Oblicz : a) sin 750⁰ ; b) tg (- 300⁰) ; c) cos 225⁰ ; d) ctg (-240⁰)

Ad. a) Zasada 1 : możesz dodawać lub odejmować (od kąta który jest w przykładzie) 360⁰ i niczym się nie przejmować.

sin 750⁰ = sin (750⁰ - 360⁰) = sin 390⁰ = sin (390⁰ - 360⁰) = sin 30⁰ = 0,5 (wynik końcowy z tabelki)

Ad. b) Zasada 2 : jeśli dadzą Ci kąt ujemny możesz dzięki zasadzie 1 ,,pozbyć” się go dodając po 360⁰ tak długo aż ujemny ,,zniknie”. Dlatego nie zawracam sobie głowy kątami ujemnymi - umiemy je ,,znikać”.

tg (-300⁰) = tg (-300⁰ + 360⁰) = tg 60⁰ =
(wynik końcowy z tabelki).................................................... cofnij

Ad. c) Zasada 3 : każdy z kątów który jest w przykładzie możesz zapisać w postaci sumy (unikaj różnicy; tak bywa w szkole i dlatego uczniowie mają kłopoty; nauczyciele nie) dwóch mniejszych kątów, ale tak aby jeden z nich był kątem osi (czyli 90⁰; 180⁰; 270⁰; 360⁰). Kąt osi może zniknąć z przykładu.

Gdy był to kąt z osi niebezpiecznej (y) to zmieniamy funkcję na tę ,,drugą”, jeśli był z osi poziomej (x) to funkcję pozostawiamy w spokoju. Niestety podczas ,,gubienia” kątów osi (nie dotyczy 360⁰ - zasada 1) musimy uważać na znaki funkcji w ćwiartkach (wierszyk).

cos 225⁰ = cos (180⁰ + 45⁰) = sprawdzamy w jakiej ćwiartce jest 180 + 45, w III ; jaki jest tam kosinus? (wierszyk) odp : ujemny(taki znak do wyniku); gubimy 180, funkcja pozostaje w spokoju(kosinus do wyniku);mamy

= - cos 45⁰ =
(wynik końcowy z tabelki)

Ad. d) ctg (-240⁰) = zasada 2 = ctg (-240⁰ + 360⁰) = ctg 120⁰ = zasada 3 = ctg (90⁰ + 30⁰) = sprawdzamy w jakiej ćwiartce jest 90 + 30, w II; jaki jest tam kotangens? (wierszyk)odp : ujemny(taki znak do wyniku); gubimy 90, zamieniamy funkcję na tę drugą(tangens do wyniku); mamy = - tg 30⁰ =
(wynik końcowy z tabelki)..

Przykład 2 : Pozwolę sobie na uproszczenie - nie będę pisał znaczka ⁰. Nie zmieni to rozumowania.................. cofnij

Oblicz : a) cos (-1290) ; b) tg 585 ; c) sin 330 ; d) ctg (- 210)

Ad. a) cos (-1290) = zasada 2 = cos (-1290 + 360 + 360 + 360 + 360) = cos 150 = zasada 3 = cos (90 + 60) =

sprawdzamy w jakiej ćwiartce jest 90 + 60, w II; jaki jest tam kosinus? (wierszyk) odp : ujemny(do wyniku); gubimy 90,zamieniamy funkcję na tę drugą(sinus do wyniku);mamy= - sin 60 =
(wynik końcowy z tabelki)

Ad. b) tg 585 = zasada 1 = tg (585 - 360) = tg 225 = zasada 3 = tg (180 + 45) = sprawdzamy w jakiej ćwiartce jest 180 + 45, w III ; jaki jest tam tangens? (wierszyk)odp : dodatni(do wyniku); gubimy 180, funkcja pozostaje w spokoju (tangens do wyniku); mamy = + tg 45 = 1 (wynik końcowy z tabelki)

Ad. c) sin 330 = zasada 3 = sin (270 + 60) = sprawdzamy w jakiej ćwiartce jest 270 + 60, w IV ; jaki jest tam sinus? (wierszyk)odp : ujemny(do wyniku); gubimy 270, zamieniamy funkcję(kosinus do wyniku); więc = - cos 60 = - 0,5 (wynik końcowy z tabelki)

Ad. d) ctg (-210) = zasada 2 = ctg (-210 + 360) = ctg 150 = zasada 3 = ctg (90 + 60) = sprawdzamy w jakiej ćwiartce jest 90 + 60, w II; jaki jest tam kotangens? (wierszyk) odp : ujemny(do wyniku); gubimy 90,zamieniamy funkcję na tę drugą(tg do wyniku); mamy= - tg 60 = -
(wynik końcowy z tabelki)

Z8. Oblicz : a) tg (-120) ; b) ctg 405 ; c) cos 2130 ; d) sin (-855).................................................................. cofnij

---