Ćwiczenie nr 8

Wyznaczanie współczynnika załamania światła metodą interferometryczną

1. Oddziaływanie światła z materią

Oddziaływanie światła z materią można przedstawić za pomocą trzech zjawisk:

• Pochłanianie fotonów (absorpcja)

• Emisja spontaniczna

• Emisja wymuszona

Absorpcja jest to pochłanianie (całkowite lub częściowe) energii promieniowania elektromagnetycznego (np. neutronów) lub energii fal dźwięku, przez ośrodek, w którym rozchodzi się to promieniowanie.

Absorpcja promieniowania zwiększa energię ośrodka, powodując np. wzbudzenie jąder atomu, cząsteczek, co może doprowadzić do reakcji jądrowych, zjawiska fotoelektrycznego, luminescencji itp.

Miarą zdolności absorpcyjnej ośrodka jest współczynnik absorpcji i zależy on od rodzaju ośrodka i długości fali (częstości drgań) promieniowania.

Emisja spontaniczna powoduje, że atomy w stanie wzbudzonym pozostają bardzo krótko, przechodząc szybko do stanu podstawowego. Niektóre atomy posiadają poziomy energetyczne metatrwałe, na których elektron pozostaje znacznie dłużej, ale w takiej sytuacji przejście ze stanu podstawowego do wzbudzonego jest utrudnione. Pokonuje się je przez wzbudzenie atomu do poziomów o energii niewiele większej od poziomu metatrwałego.

Emisja wymuszona jest to emisja fotonów pod wpływem zewnętrznego pola elektromagnetycznego. Foton ten jest spójny (ma taką samą częstotliwość, polaryzację) z fotonem wywołującym emisję. Foton wzbudzający musi mieć odpowiednią energię równą energii wzbudzenia ośrodka. Atomy w stanie podstawowym pochłaniają fotony wzbudzające.

2. Interferencja i dyfrakcja światła.

O interferencji mówimy wtedy, gdy dwa jednakowe ciągi fal nakładają się na siebie wyniku, czego może nastąpić ich wzmocnienie lub wygaszenie w zależności od tego czy są przesunięte czy zgodne w fazie.

Dyfrakcją nazywamy ugięcie się fali na krawędziach wąskiej szczeliny. Jest ono znaczące wtedy, gdy rozmiary szczeliny są porównywalne z długością fali. Szersze szczeliny powodują mniejsze ugięcie.

Przechodząc przez ten sam punkt w przestrzeni dwa ciągi fal nie oddziałują na siebie, jednak nakładają się na siebie i wypadkowe wychylenie jest sumą (wektorową) wychyleń spotykających się ciągów - zasada superpozycji.

O interferencji konstruktywnej mówimy, gdy spotykają się fale zgodne w fazie i wzmacniają wzajemnie, a o destruktywnej mówimy, gdy spotykają się fale o różnicy fal ½ okresu i wygaszają wzajemnie.

Aby można było obserwować interferencję:

• ciągi fal muszą być spójne, czyli ich różnica faz musi być stałą, zatem ich częstotliwości muszą być jednakowe

• ciągi fal muszą mieć w przybliżeniu jednakowe amplitudy i tą samą płaszczyznę drgań

Fale wysłane ze spójnych źródeł tworzą obszary wzmocnienia i wygaszenia, zwane obrazem interferencyjnym. W każdym punkcie, gdzie zachodzi interferencja konstruktywna droga do jednego źródła jest taka sama jak droga do drugiego źródła lub jest od niej dłuższa

Poszerzenie światła po przejściu przez szczelinę jest przykładem dyfrakcji fal. Między różnymi falami ugiętymi na szczelinie zachodzi interferencja. Obraz interferencyjny staje się szerszy, kiedy doświadczenie przeprowadza się z ugiętą szczeliną lub ze światłem o większej długości fali.

d sinγ = n λ

3. Równanie Clausiusa-Mossattiego.

Polaryzowalność na mol wyrażam wzorem:

(1)

M - masa drobinowa

- gęstość

Wektor polaryzacji jest związany z polaryzowalnością równaniem:

-polaryzowalnośc

- wektor polaryzacji

- pole lokalne

N - polaryzowalność na jednostkę objętości

=

Z czego otrzymujemy:

lub:

(2)

-podatność elektryczna ośrodka

Na podstawie 1 i 2 otrzymujemy RÓWNANIE CLAUSIUSA-MOSSATTIEGO w który jedynym parametrem nieznanym jest polaryzowalność

Prawą stronę równania nazywamy refrakcją molową i oznaczamy R.

Z równania Clausiusa-Mossattiego wynika, że refrakcja molarna jest wielkością stałą z pominięciem oddziaływania otoczenia na drobiny dielektryka.

4. Refrakcja.

Refrakcja jest to zmiana kierunku czoła fali padającej ukośnie na granicę dwóch ośrodków przy przechodzeniu przez tą granicę. Związana jest z różnicą prędkości rozchodzenia się w obu ośrodkach. Zjawisko to zachodzi dla wszystkich rodzajów fal świetlnych. W optyce kierunek rozchodzenia się fali ulega zmianie zgodnie z prawem Snella tj. n₁ sinγ = n₂ sinθ

gdzie γ i θ są kątami jakie z normalną (linią prostopadła do płaszczyzny granicznej) między dwoma ośrodkami, tworzy odpowiednia wiązka padająca i wiązka załamana. Prawo to jest również znane jako jedno z prawo załamania.

5. Interferometry. Zasada działania i rodzaje.

Zjawisko interferencji światła wykorzystywane jest w szeregu bardzo dokładnych przyrządów pomiarowych, nazywanych interferometrami.

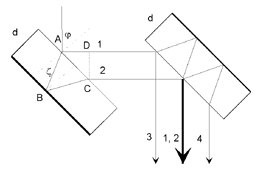
Rys.1. Schemat interferometru Jamina

Schemat przedstawia interferometr Jamina. Dwie dokładnie jednakowej grubości płytki szklane A i B ustawione są w stosunku do siebie prawie równolegle. Promienie świetlne ze źródła monochromatycznego padają na powierzchnię płytki A pod różnymi kątami. Prążki interferencyjne ogląda się przez okular. Jeżeli jedna z kuwet, znajdujących się na drodze promieni, napełniona jest gazem o znanym wsp. załamania n, a druga gazem, którego wsp. załamania chcemy zmierzyć, to różnica dróg optycznych między interferującymi promieniami wynosi
. Więc

gdzie m - rząd max. interferencyjnego. Zmiana różnicy n₂-n₁ powoduje przesunięcie prążków interferencyjnych.

Zasadą działania wszystkich interferometrów optycznych jest rozdzielenie wiązki fal na promienie biegnące po różnych drogach optycznych, a następnie doprowadzenie do interfererencji tych promieni.

Typowymi interferometrami są: interferometry Fabry'ego-Perota, Jamina, Macha-Zehndera, Michelsona, Rayleigha, Twymana-Greena.

W interferometrze Michelsona równoległa wiązka światła pada na półprzepuszczalne zwierciadło i zostaje rozdzielona na dwie wzajemnie prostopadłe wiązki, które po odbiciu od zwierciadeł wracają do półprzepuszczalnego zwierciadła i są ponownie łączone w jedną wiązkę, w której zachodzi interferencja. Interferometr Michelsona posłużył do wykonania słynnego doświadczenia Michelsona-Morleya, wykazującego stałość prędkości światła w każdym układzie odniesienia. Interferometr Michelsona znajduje szerokie zastosowanie w technice.

6. Interferometr laboratoryjny LI-3.

Rayleigha interferometr, refraktometr interferencyjny, rodzaj interferometru optycznego służący do bardzo precyzyjnego pomiaru różnicy współczynnika załamania światła dwóch ośrodków.

Zbudowany jest ze źródła światła, obiektywu, diafragmy z dwiema szczelinami dyfrakcyjnymi (dyfrakcja fal), dwóch naczyń wypełnionych wzorcową i badaną substancją oraz lunetki z okularem cylindrycznym. Źródło światła umieszczone jest w ognisku obiektywu, powstała po przejściu przez obiektyw równoległa wiązka światła trafia na diafragmę o dwóch równoległych, pionowych szczelinach, gdzie zachodzi zjawisko dyfrakcji światła. Przestrzeń za każdą ze szczelin od połowy jej wysokości wypełniają odpowiednio naczynia z badaną i wzorcową substancją. Ugięte promienie interferują (interferencja fal) ze sobą, przy czym światło ugięte w górnej połowie przyrządu (ze względu na rozprzestrzenianie się w ośrodkach o różnych współczynnikach załamania światła) tworzy układ prążków interferencyjnych przesunięty względem układu prążków powstających w dolnej części przyrządu.

Pomiar przesunięcia prążków pozwala wyznaczyć względny współczynnik załamania światła z dokładnością nawet do 8 cyfr znaczących.

Wykonanie ćwiczenia:

Celem ćwiczenia był pomiar zależności współczynnika załamania światła od ciśnienia dla powietrza w danej temperaturze.

W tym celu:

1. Odczytałam temperaturę T=23^oC.

2. Zamocowałam kuwetę czerwoną kropką w stronę okularu i podłączyłam do układu próżniowego.

3. Kurek 1 ustawiłam w pozycji Z (zapowietrzanie pompy), natomiast kurek 2 w pozycji pompującej obie komory. Kurek 3 pozostawiam zamknięty.

4. Włączyłam pompę rotacyjną, przekręciłam kurek 1 o 180^o i pompowałam obie komory przez koło 10 minut.

5. Osoba wykonująca ze mną ćwiczenie ustawiła ostrość prążków, odaretowałą śrubę mikrometryczną, wyzerowała i zaaretowała.

6. Kurek 2 ustawiłam w pozycji odpompowania komory I i odcięcia komory II.

7. Przy pomocy kurka 3 zmieniałam ciśnienie w komorze II i jednocześnie dopasowywałyśmy obraz górnych prążków do dolnych. Odczytałyśmy z bębna różnicę dróg optycznych odpowiadającą ustawieniu ciśnienia. Zanotowałyśmy wyniki.

8. Czynności te wykonałyśmy dla kuwet o długości l=10cm, l=25cm i l=50cm.

Opracowanie wyników

1. Obliczanie współczynników załamania światła dla poszczególnych ciśnień wg wzoru
   

I KUWETA L = 10 cm = 100mm

Dla p = 75 hPa

Dla p = 165hPa

Dla p = 245 hPa

Dla p = 330 hPa

Dla p = 440 hPa

Dla p = 550 hPa

Dla p = 640 hPa

Dla p = 740 hPa

Dla p = 840 hPa

Dla p = 950 hPa

Dla p = 1000 hPa

II KUWETA L =25 cm = 250mm

Dla p = 75 hPa

Dla p = 120 hPa

Dla p = 190 hPa

Dla p = 260 hPa

Dla p = 310 hPa

Dla p = 380 hPa

Dla p = 460 hPa

Dla p = 580 hPa

Dla p = 610 hPa

Dla p = 710 hPa

Dla p = 800 hPa

III KUWETA L =50 cm = 500mm

Dla p = 50 hPa

Dla p = 110 hPa

Dla p = 180 hPa

Dla p = 230 hPa

Dla p = 280 hPa

Dla p = 340 hPa

Dla p = 370 hPa

Dla p = 420 hPa

Obliczanie gęstości powietrza dla poszczególnych ciśnień wg wzoru

I KUWETA t = 23⁰C

Dla p = 75 hPa

Dla p = 165 hPa

Dla p = 245 hPa

Dla p = 330 hPa

Dla p = 440 hPa

Dla p = 550 hPa

Dla p = 640 hPa

Dla p = 740 hPa

Dla p = 840 hPa

Dla p = 950 hPa

Dla p = 1000 hPa

II KUWETA t = 23⁰C

Dla p = 75 hPa

Dla p = 120 hPa

Dla p = 190 hPa

Dla p = 260 hPa

Dla p = 310 hPa

Dla p = 380 hPa

Dla p = 460 hPa

Dla p = 580 hPa

Dla p = 610 hPa

Dla p = 710 hPa

Dla p = 800 hPa

III KUWETA t = 23⁰C

Dla p = 50 hPa

Dla p = 110 hPa

Dla p = 180 hPa

Dla p = 230 hPa

Dla p = 280 hPa

Dla p = 340 hPa

Dla p = 370 hPa

Dla p = 420 hPa

Obliczanie wartości refrakcji właściwej wg wzoru

I. KUWETA

II. KUWETA

III. KUWETA

WNIOSKI

Celem ćwiczenia było wykonanie pomiaru zależności współczynnika załamania światła od ciśnienia w danej temperaturze. Po wykonaniu pomiarów obliczono ze stosownych wzorów współczynniki załamania światła, gęstość powietrza oraz refrakcje właściwą.

Otrzymane wyniki są do siebie zbliżone. Niepewności pomiarowe wiążą się z niemożliwością dokładnego odczytu różnicy dróg optycznych.Odczyt był bardzo niewyraźny, co wiążę się z powstawaniem wielu błędów.

.

7

---