0. Prawo Coulomba a prawo Gaussa dla elektrostatyki, w postaci całkowej i różniczkowej ( analogie z polem grawitacyjnym).

Q

r'

o SD'

r

q

Ładunek Q wytwarzający pole elektrostatyczne umieszczony jest w punkcie którego położenie wyznacza wektor położenia r' w pewnym układzie odniesienia O. Jeżeli w punkcie wyznaczonym przez wektor położenia r zostanie umieszczony ładunek próbny q, to na ten ładunek będzie działać siła F dana prawem Coulomba:

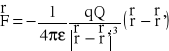
Tak jest w przypadku pojedynczego ładunku punktowego. Zaś pole wytworzone przez dowolny układ ładunków jest sumą pól pochodzących od poszczególnych ładunków:

Mamy więc N ładunków punktowych Q₁,Q₂,...,Q_N znajdujących się w punktach r_1, r_2, .....r_N. Dla i-tego ładunku siła z jaką działa on na ładunek próby jest równa :

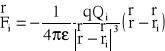
Natomiast wektor siły pochodzący od układu N ładunków punktowych jest :

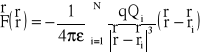
Jeżeli mamy układ bardzo dużej liczby ładunków punktowych rozłożonych w pewnej ograniczonej objętości, należy przejść do rozkładu ładunku. Gęstość ładunku w punkcie r' jest równa:

Element objętości dV oznaczamy przez d³r' i mamy:

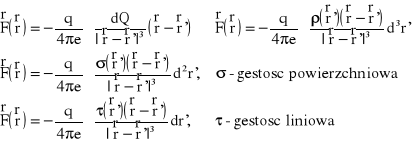
Ładunek punktowy Q wytwarza wokół siebie pole elektrostatyczne. Ładunek ten jest otoczony powierzchnią zamkniętą S, którą dzielimy na infinitezymalnie małe części dS. Strumień pola elektrycznego przenikającego przez powierzchnię S jest równy:

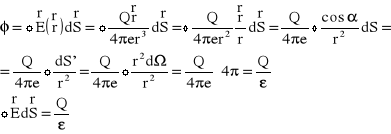
Natomiast jeśli ładunek Q znajduje się na zewnątrz powierzchni zamkniętej, to strumień pola tego ładunku przez tę powierzchnię jest równy zero. A więc tw. Gaussa dla elektrostatyki możemy zapisać następująco:

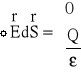
Natomiast dla pola elektrostatycznego dowolnego rozkładu ładunku
prawo Gaussa jest następujące:

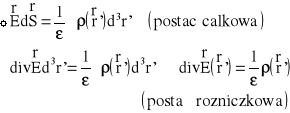
Analogie:

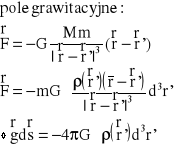
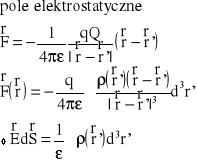
1 Równania Maxwella dla elektrostatyki.

Prawo Gaussa dla elektrostatyki ma postać:

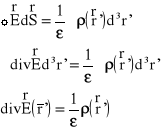
Do tego prawa Gaussa w postaci różniczkowej dołączamy równanie na rotację i mamy układ równań :

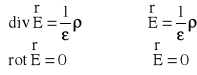
Są to równania Maxwella w postaci różniczkowej. Natomiast w postaci całkowej są następujące:

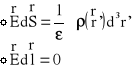
Wektor indukcji elektrostatycznej
i dla ośrodków jednorodnych mamy :

Równanie
stwierdza, że źródłem pola elektrycznego wektora indukcji elektrostatycznej są ładunki swobodne lub ich rozkład gęstości. Pole tego wektora jest więc polem źródłowym.

2 Równanie Poissone'a i Laplace'a dla pola elektrostatycznego.

Należy wyjść od równań Maxwella dla elektrostatyki:

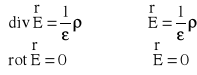
Do równania
podstawiamy
, ale natężenie pola możemy wyznaczyć poprzez potencjał elektrostatyczny
.

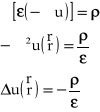
Jest to równanie Poissone'a.

Jeżeli w ośrodku nie ma ładunków swobodnych (ρ, to z równania Poissone'a otrzymamy równanie Laplace'a:
. Równanie to służy do znajdowania potencjału elektrostatycznego w ośrodku, w którym nie ma ładunków swobodnych.