9 Natężenie i potencjał wektorowy pola magnetycznego.
Do całkowej postaci prawa Biota-Savarta:
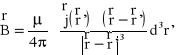
podstawiamy związek:
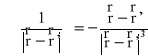
i mamy związek:
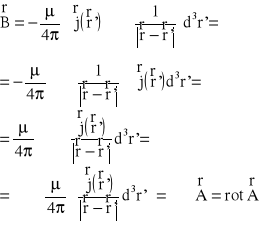
Jest to różniczkowa postać prawa Biota-Savarta, które wiąże ze sobą wektory indukcji magnetycznej B i potencjału wektorowego A pola magnetycznego.
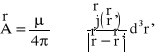
Potencjał ten jest określony z dokładnością do stałej. Jeżeli do A dodać gradient dowolnej funkcji skalarnej, to rotacja z A nie zmieni się.
![]()
W ten sposób potencjał wektorowy można cechować tak, aby były spełnione dodatkowe warunki. W magnetostatyce przyjmuje się cechowania postaci : ![]()
.
Dla magnetyków stosuje się następujące równania materiałowe:
![]()
, gdzie H jest wektorem natężenia pola magnetycznego.
10 Równania Maxwella dla magnetostatyki.
Wektor indukcji magnetycznej B opisuje pole magnetyczne, którego linie sił nie mają początku ani końca. Dlatego strumień pola wektorowego indukcji magnetycznej przez dowolną powierzchnię zamkniętą jest równy zero:

Oznacza to, że pole magnetyczne jest polem bezźródłowym albo przepływowym. Pole wektorowe, którego dywergencja jest równa zeru można przedstawić w postaci rotacji z innego wektora.
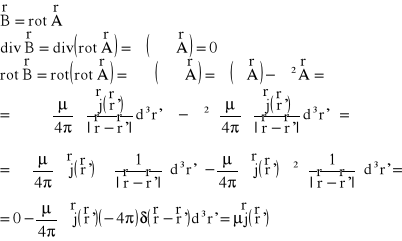
Oznacza to, że pole magnetyczne jest polem zachowawczym.
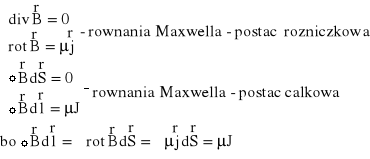
Krążenie z wektora B po krzywej zamkniętej obejmującej powierzchnię S jest równe prądowi całkowitemu przepływającemu przez tę powierzchnię.
11. Równania Maxwella dla prądu zmiennego, prąd przesunięcia.
Prawo Faraday'a dla dowolnego przewodnika zamkniętego jest następujące:
![]()
Dowolny obwód zamknięty porusza się ze stałą prędkością względem pewnego inercjalnego układu odniesienia.
![]()
Jeśli układ się porusza, to pełna zmiana wektora indukcji B:

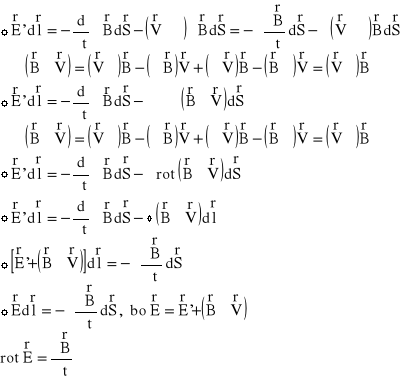
W ten sposób otrzymaliśmy pierwszą parę równań Maxwella:
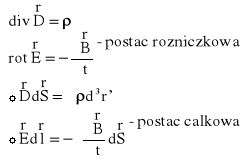
Równanie ciągłości wymaga, aby szybkość zmiany ładunku w pewnej objętości była równa całkowitemu strumieniowi gęstości wektora prądu wypływającego z tej objętości przez powierzchnię ograniczającą tę objętość.

W ten sposób otrzymaliśmy drugą parę równań Maxwella:
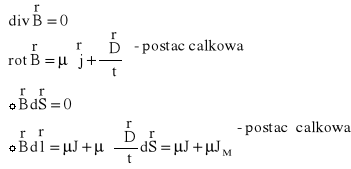
Wyszukiwarka
Podobne podstrony:
5561, Studia, Elektronika, Rok I, fizyka, labo
12, Studia, Elektronika, Rok I, fizyka, labo
6, Studia, Elektronika, Rok I, fizyka, labo
M7, Studia, Elektronika, Rok I, fizyka, labo
Przebieg ćwiczenia fizyka cw 3stary, Studia, Elektronika, Rok I, fizyka, Fizyka lab - sprawozdania,
ELEKTROSTATYKA , Studia, BUD 1 rok, Fizyka
F10- sprawozdanie Wojtka, STUDIA (ochrona), ROK I, Fizyka, laboratoria
Gęstość i ciężar właściwy, Studia, II rok, fizyka
Lab Fiz322a, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 31, Studia, II rok, Fizyka Eksperymentalna
dioda- sprawozdanie, Studia, II rok, fizyka
Spr 42, Studia, II rok, Fizyka Eksperymentalna
oscyloskop-obliczenia, STUDIA (ochrona), ROK I, Fizyka, laboratoria
Fizyka1, Studia, II rok, Fizyka Eksperymentalna
laborki34, Studia, II rok, fizyka
laborki10, Studia, II rok, fizyka
Sprawko 48-fiza, Studia, II rok, fizyka
Cwiczenie 19, Studia, II rok, Fizyka Eksperymentalna
więcej podobnych podstron