t> t:N-2

1. Czym różnią się czynniki o charakterze losowym od czynnikow o charakterze stałym Czynnik stały: rozkład o różnym charakterze

-Liczba poziomów niewielka, a analizie uwzględnia się zwykle konkretne z góry określone poziomy czynnika

1. Wnioskowanie ograniczone do poziomów czynnika uwzględnionego w analizie

2. Sezon, rok, stado, typ, Płeć

Czynnik losowy: rozkład normalny

1. Liczba poziomów duża, analizowany jest losowy podział wszystkich poziomów czynnika

2. Warunkowanie: uogólnienie wniosków na wszystkie, również nie analizowane, poziomy czynnika

3. Grupa genetyczna, ojciec, linia, rasa

Czynnik stały ma rozkład o różnym charakterze a losowy- rozkład normalny

2. W jaki sposób i po co przeprowadza się standaryzacje?

Standaryzacja to liniowe przekształcenie w wyniku którego otrzymujemy zmienna losowa o wartości oczekiwanej = 0 i odch.stan.=1; Cel: odczytanie z tablic rozkładu normalnego

3. Wymienić cechy jakie powinien posiadać dobry estymator.

Nieobciążoność – wartość oczekiwana estymatora jest równa estymowanemu parametrowi E(T_N)=

Zgodność – estymator jest zgodny gdy jest stochastycznie zbieżny do szacowanego parametru czyli lim PT_N-=1 Średnia i mediana SA estymatorami zgodnymi gdyż gdy zwiększa się liczebność próby SA bliskie wartości oczekiwanej

Efektywność- estymator jest najefektywniejszy gdy jego wariancja jest najmniejsza

Dostateczność- gdy estymator uwzględnia wszystkie informacje z próby czyli jest funkcja wszystkich elementów próby

4. Jaka jest interpretacja współczynnika korelacji i regresji? Jakie wartości mogą przyjmować te parametry?

wsp. korelacji- wskazuje na zależności m. cechami, przyjmuje wartości od –1 do 1. Jeżeli 0 to nie ma zależności, im bliżej –1 lub 1 tym korelacja silniejsza. Znak wskazuje na kierunek zależności, Jeżeli dodatki to proporcjonalna jeżeli ujemny to odwrotnie.

Wsp. regresji= przyrost cechy zależnej przypadający na przyrost o jednostkę cechy niezależnej

przyjmuje wartości ze zbioru liczb rzeczywistych, a jej znak jest taki sam jak współczynnika korelacji (+/-)

5. Jakie są cech krzywej Gaussa

Krzywa Gaussa to wykres funkcji gęstości rozkładu normalnego. Położenie i kształt zależą od wartości oczekiwanej i odchylenia standardowego. Symetryczna względem prostej x=m(=M_e=M_o) f.gęstości osiąga max dla EX, stad wartość oczekiwana, mediana i dominanta są sobie równe

6. Jakimi cechami powinny charakteryzować się reszty w analizie regresji

Powinny mieć rozkład normalny, Być losowe, Ich wariancja powinna być stabilna

6. Od czego zależy wielkość a od czego położenie obszaru krytycznego pod krzywą rozkładu

Wielkość zależy od poziomu ufności a położenie od przyjętej hipotezy- tzn. od tego czy hipoteza jest prawo, lewo czy obustronna nie od testu tylko od przyjętej hipotezy- tzn. od tego czy hipoteza jest prawo, lewo czy obustronna)

8. Jak zmieni się długość przedziału ufności dla prawdopodobieństwa sukcesu gdy (częstość empiryczna wzrośnie o 0,1))liczebność próby wzrośnie o 44%(21%). Jakie inne czynniki w jaki sposób wpływają na długość przedziału ufności dla prawdopodobieństwa

Długość przedziałów ulegnie skróceniu (będzie dokładniejszy)

Inne czynniki:

-Odchylenie standardowe – im większe tym przedział dłuższy -Poziom ufności - im większy tym przedział dłuższy -Wartość empiryczna – gdy=1/2 przedział najdłuższy

P(w-Ualfa*pierwiastek z w-(1-w)/N <p<w+ Ualfa*pierwiastek z w(1-w)/N=1-alfa w- cz. empiryczna

N wzrosło 1,44 razy, czyli przedział skróci się pierwiastek z 1,44 razy, czyli przedział skróci się 1,2 razy, czyli o 20%

Dł.przedziału zależy: odwrotnie proporcjonalnie od poziomu istotności () i liczebności próby, a wprost proporcjonalnie od odchylenia stand. w próbie

9. Dwie osoby wyznaczyły sobie godzinę spotkania między 9 a 10 (11). Każda z nich może pojawić się o dowolnej porze i będzie czekać dokładnie 20 min. Jakie jest prawdopodobieństwo że osoby się spotkają.?

Pole trójkąta = 1,2*a*h=1/2*2/3*2/3=2/9

P=1-2*pole trójkąta=1-2*2/9=5/9=0,56 1-(2/9+2/9)=5/9

Zad z godz 11 odp 11/36

10. Czy przedział ufności dla prawdopodobieństwa P(0,35<p<0,47)=0,96 jest precyzyjny.

X1=0,35 x2=0,47

W=x1+x2/2= 0,35+0,47 / 2 = 0,41 d=s-w = 0,47 – 0,41 = 0,06

…=d / w * 100% = 0,06/0,41 *100% = 14, 6 0% - 5% - duża precyzja

5% -10% - mała precyzja

10% - - brak precyzji

odp.: przedział nie jest precyzyjny

11. Ocenić istotność współczynnika korelacji jeśli w próbie o N=18 uzyskano następujące wartości liniowych współczynników bx =0,2 i by= 3,2

Ho wsp. Korelacji jest nie istotny  = 0,05 H₁ wsp. Korelacji jest istotny

r- wsp. Korelacji

r= pierwiastek bx*by = pierw. 0,2*3,2 = pierw. 0,64 = 0,8 r>0 bo bx>0, r<0 gdy bx<0

t_emp=r_xy / pierw 1-(0,8)² / N-2 =0,8 / pierw.1-0,64/16 = 0,8/0,15=5,1/3 alfa0,05 – 2,120, 5,333>2,120

(jeśli w zad N=27 to wszystko =6,67) t_:N-2 = t _0,05:25 = 2,060 (z tab t-Studenta)

6,67>2.060 Ho odrzucamy, wsp. Korelacji jest istotny

12. Na ruchliwym skrzyżowaniu zdarza się rocznie 36 wypadków. Jakie jest prawdopodobieństwo ze w danym miesiącu zdarza się: A Dokładnie 3 wypadki

B Co najwyżej 1 wypadek

Skoro mamy wypadków rocznie 36 a rozpatrujemy prawdopodobieństwo w miesiącu to liczymy ile średnio wypadków będzie w miesiącu

36/12=3 czyli EX=3

z właściwości rozkładu Poissona wiemy, że EX=lambda (nie wiem jak to wstawić w Wordzie) stąd lambda=3 a)dokładnie 3 wypadki:

P(k=3)=0,2240 (z tablic Poissona, gdzie k=3 i lambda=3) b)co najwyżej jeden wypadek

P(k≤1)=P(k=0)+P(k=1) = 0,0498+0,1494=0,1992

13. Wiadomo że masa jaj ma rozkład normalny o 62g i 10g. Jeden producent sprzedaje jaja w cenie 40gr za szt. Drugi producent dzieli jaja na 3(4) klasy: małe do 50 g, średnie(do 65) i duże do 70g,i bardzo duże do 75g. Cena jajka małego wynosi 45gr(35gr). średniego 40gr a dużego 50gr.(i bardzo dużego 55 gr.) Który producent zarabia więcej? Jeśli z nich każdy sprzeda 10 tys. jajek to jaka ich część jest sprzedana po 40 gr.?

u=60 odchylenie=10

P(x<50) = F(z=x-u/odch) =F(z=50-62/10) = F(z= -1,2) = 1-F(Z=1,2) = 1 – 0,8849=0,1151 P(x<70) = F(z=70-62/10) = F(z=0,8) = 0,78814

I producent

Małe P (x<50) = 0,1151

Średnie P(50<x>70) = 00,7881-0,1151=0,637 Duże P(x>70) = 1 – 0,7881=0,2119

II producent

Małe poniżej 50 koszt 40 gr. Średnie od 50 koszt 45 gr. Duże powyżej 50 koszt 50 gr.

Średnia cena jajek 0,1151*0,35+0,673*0,40+0,2119+0,50=0,4154 Odp.” II producent zarabia więcej.

II część

N(62:10) u=62 s=10

Małe P(x<50)=P(50-62/10)=F(z=-1,2)=1-0,8849=0,1151

Średnie P(50<x,<65)=F(65-62/10)-F(z=-1,2)=F(z=0,3)-1-F(z=-1,2)=0,61791-(1-0,8849)=0,50284 Duże P(65<x<70)=F(z=70-62/10)-F(z=0,3)=F(z=0,8)-F(z=0,3)=0,78814-0,61741=0,17023 b.duże P(70<x<75)=F(z=75-62/10)-F(z=0,8)=0,90320-0,78814=0,11506

I prod. 10000*0,40 100% sprzeda IIprod. 0,9032 – 100%

0,50284 – x x=0,55673=55% 10000*0,55673*0,40=2226,92 tyle zarabia

14. Czy liniowa funkcja regresji o R²=0,6 jest istotna jeśli próba liczy 7 obserwacji

Tak, gdyż przy tak niewielkiej próbie R²=0,6 świadczy o dobrze dopasowanej funkcji

R²=0,6 N=7 R²=SSR/SSR+SSE=0,6

Femp= SSR(N-k)/SSE (k-1) k-1=1 bo f. liniowa N-1=6 SSR/(SSR+SSE)=0,6 I: (SSR+SSE)

SSR=0,6(SSR+SSE)

SSR-0,6SSR=0,6SSE 0,4SSR=0,6SSE SSR= -1,5SSE 6*1,5SSE/SSE=x X=9

Femp=9

F=o,o5;1;6=5,99

F=o,o1;1;6=13,75

15. Co można powiedzieć o zmienności próby jeśli miary rozrzutu wartości zmiennej mają taką samą wartość (jaką?).zmienność nie występuje, miary rozrzutu mają wartość 0

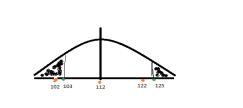
15. Stwierdzono, że masa ciała tuczników podlega rozkładowi normalnemu o wartości średniej 112kg. Proszę wyjaśnić, które z dwóch prawdopodobieństw będzie większe P(x>125) czy P(X<103)

Przy założeniu s=5 P(125<x<nieskończoność)=F(x=niesk)-F(x=125)=1-0,99534=0,00466 F(z=125-112/5)=F(2,6)=0,99534 P(-niesk<x<103)=F(x=103)-F(x=-niesk)=0,03593-0=0,03593 F(z=103-112/5)=F(z=-1,8)=1-F(z=1,8)=1-0,96404=0,03593 P(x=103)>P(x=125)

17. Dlaczego w testach istotności nie można przyjmować Ho?

Test istotności – rodzaj testu, w którym na podstawie wyników próby losowej podejmuje się tylko i wyłącznie decyzje odrzucania hipotezy, którą się sprawdza, bądź stwierdza się brak podstaw do odrzucenia jej hipotezy

W teście istotności nie podejmuje się decyzji o przyjęciu sprawdzonej hipotezy, ponieważ bierze się w tym teście pod uwagę tylko błąd pierwszego rodzaju, a jego prawdopodobieństwo to poziom istotności, nie uwzględnia się natomiast konsekwencji popełnienia błędu drugiego rodzaju.

W każdym teście istotności możemy się pomylić i odrzucić hipotezę, która była prawdziwa(błąd pierwszego rodzaju), ale prawdopodobieństwo takiej pomyłki jest bardzo małe, równe obranemu alfa.

18. Co to jest histogram i w jaki sposób można go uzyskać

To zestawienie danych statystycznych w postaci wykresu powierzchniowego złożonego z przylegających do siebie słupków ( prostokątów), których wysokości ilustruje liczebność występowania badanej cechy w populacji lub jej próbie, a podstawy (które spoczywają na osi odciętych) są rozpiętościami przedziałów klasowych.

Taki sposób konstrukcji histogramu jest stosowany wówczas kiedy przedziały szeregu rozdzielczego są równe. Jeżeli szereg ma nierówne przedziały, to wysokość prostokątów określona przez wskaźnik natężenia liczebności (częstości)odpowiadające poszczególnym klasom

Histogram to graficzne przedstawienie rozkładu empirycznego cechy. Szereg prostokątów na osi współrzędnych wyznaczonych przez przedziały klasowe , wartości cechy a wysokość, liczebność elementów podziałów.

19. Wiedząc że P(B) =2/3, P((AB)=1/4, Obliczyć P(AB)

P(AB)= P(A) + P(B); P(AB)= P(A) * P(B) niezależnie

P(A/B)= ^{P(A  B)} (pod warunkiem)

P(B)

P(A/B) = P(AB ) / P(B) P(B) = 2/3 =0,6 P(A/B)=1/4 =0,25

P((AB)=P(A/B)*P(B)=0,25*0,6 =0,15

20. Czym się różnią i jaki mają związek niezależność stochastyczna i korelacyjna?

Niezależność stochastyczna występuje gdy rozkłady warunkowe jednej zmiennej dla wartości drugiej zmiennej są jednakowe.

Natomiast mówimy, że zmienne są niezależne korelacyjnie, jeśli warunkowe wartości oczekiwanej jednej zmiennej są jednakowe dla każdej wartości drugiej zmiennej.

Niezależność stochastyczna implikuje niezależność korelacyjną, ale nie odwrotnie.

mediana i dominanta są sobie

21. Średnio liczba bakterii w kropli substancji jest równa 0,2 (0,5, 0,25). Z ilu kropli należy utworzyć próbkę substancji aby z prawdopodobieństwem 0,95 znalazła się w niej co najmniej jedna bakteria?

Średnia liczba bakterii w kropli substancji jest równa 0,5. Rozkład liczby bakterii kropli wody jest rozkładem Poissona o lambda=0,5, w dwóch kroplach wody liczba bakterii będzie miała rozkład o lambda=1,0 itd.. Trzeba obliczyć liczbę kropli aby P(X> 1) było równe 95%.

Przeciwnym zdarzeniem do „co najmniej jedna bakteria” jest zdarzenie „brak bakterii”, tzn.

P(X>1)=1-P(X=0). Skoro P(X>1)=0,95, to P(X=0)=1+ - P(X>1)=1-O,95=0,05.

6 kropli substancji powoduje że szansa braku bakterii jest poniżej 0,05, a dopiero dla 10 kropli ta szansa jest mniejsza niż 1%. Rozkład Poissona!

Lambda to 0,62 (w 1 kropli), w 2 kroplach 1.24, w 3 - 1.86 itd.

Co najmniej jedna bakteria to P(X≥1)= 0.99, przeciwne zdarzenie to brak bakterii, czyli P(X=0) = 1-P(X≥1) = 1-0.99= 0.01

Liczba kropli	1	2	3	4	5	6	7	8
Lambda	0.62	1.24	1.86	2.48	3.1	3.72	4.34	4.96
P(X=0)	0.538	0.289	0.156	0.084	0.045	0.024	0.013	0.007

1-0.07= 0.993, czyli potrzeba 8 kropli, by z prawdopodobieństwem 0,99 w próbce znalazła się 1 bakteria.

22. Współczynnik zbieżności cech X i Y wynosi 0,25. Wiadomo ze próba liczyła 100 osobników. Czy zależność miedzy cechami jest istotna

rxy = 0,25 N=100

t_emp = rxy / pierwiastek z 1-(rxy)²/N-2

t_emp=0,25 / pierwiastek z 1-(0,25)²/100-2 = 0,25 / pierw 1-0,0625/98=0,25/ pierw0,9375/98= 0,25/0,0978 = 0,2556

 z tablic _=0,05=2,365 _0,01=2,626 2,556>2,365 odp.: jest istotny ale r2 wysokie

Dopasowanie modelu jest tym lepsze im wartość r2 jest bliższa 0

23.Próba służąca weryfikacji hipotezy o zgodności rozkładu normalnego o nieznanym odchyleniu standardowym, a o znanej średniej liczyła 250 obserwacji i była przedstawiona w postaci 6-przedziałowego szeregu rozdzielczego. Obliczono wielkość chi2emp= 13,5. Zinterpretować podane wyniki.

K=6 r=1 chi²=13,5 chi²_;k-k1-r =chi²_0,05;4=9,488

Ho cechy maja rozkład normalny

H1 nie maja

Chi²>chi² odrzucamy Ho

Cechy nie maja rozkładu normalnego

24.Wiedzac że udział 4 fabryk w dostawach do sklepu jest jednakowy oraz suma ich warunkowych prawdopodobieństw wadliwości wynosi 0,14, jakie jest prawdopodobieństwo kupienia wadliwej puszki w sklepie

N=100 P=0,14 alfa=100*0,14 – puszki wadliwe

P(xi=k)=	^k	 e ^  ; e= 2,7182 |
	k!
1 wadliwa P(x=1) 1,4 / 1!*e^-1,4=0,3452
2 wadliwe P(x=2)1,4 / 2!* e^-1,4 =0,2417
Co najmniej 2 złe P(x>2) = 1-{P(x=1)+P(x=0)}
Bez złych P(x=0)=0,2466 3 złe P(x=3) = 0,1128
Więcej niż 3 P(x=3)=1-P(x<3)=1-{P(x=1)+P(x=2)+P(x=3)}
P(x>3)=1-P(x<3)=1-{P(x=0)+P(x=1)+P(x=2)
¼*0,14=0,25*0,14=0,035
25. Jakie są własności dystrybuanty?
- ograniczona od 0 do 1, co wynika z definicji prawdopodobieństwa
- niemalejąca
- co najmniej prawostronnie ciągła
- określona dla wszystkich licz rzeczywistych
26. Parametry zmiennej losowej
- EX –wartość oczekiwana
- D^2X –wariancja
-DX – odchylenie standardowe
- inne Np. kwantyle, mediana, wartość modalna itd.
27. Jakie własności ma funkcja rozkładu zmiennej losowej?
Funkcja F(x) ma własności
-jest ograniczona				LSS	SKO	ŚKO
0<f(x)<1 – dla zmiennej losowej skokowej			Ogólne	22	166 So-S2
F(x)>0 – dla zmiennej losowej ciągłej				N-1
- Suma wszystkich wartości funkcji równa się 1			Miedzy	3-1=2 k-	86 S1-S2	86/2=43
			miej.zam.	1		SKO/LSS
Własności rozkładu normalnego zmiennej losowej X			błędu	20 N-k	80 So-S1	80/20=4
- każdy rozkład jest jednoznacznie określony przez swoje dwa parametry: wartość oczekiwaną(u) i						SKO/LSS
odchylenie standardowe (sigma), co zapisujemy…….

- rozkład normalny jest symetryczny względem prostej x=u, funkcja gęstości osiąga maksimum dla EX, stąd wartość oczekiwana, równe: EX=u=Mo=Me

= prawdopodobieństwo występowania wartości zmiennej losowej w przedziałach liczbowych o końcach wyznaczonych przez parametry rozkładu (u i sigma) tej zmiennej jest jednakowe dla każdej zmiennej o rozkładzie normalnym. Zasada nazywana regułą trzech sigm.

28.Przeprowadzono analizę wariancji w celu sprawdzenia czy istnieje różnica w ilości czasu poświęcanego dokształcaniu w zależności od miejsca zamieszkania( duże miasto, małe miasto, średnie miasto, wieś).Czy istnieje różnica między ilością czasu poświęconego na dokształcanie w zależności od miejsca zamieszkania?

.H0: d.miasto= m.miasto=przedm.=wieś

Weryfikacja H-> porównanie Femp. z wart krytyczną rozkł F-Sned. dla st.sw k-1 i N-k. Obszar krytyczny jest prawostronny.(jeżeli jest większe- odrzucamy) Femp=ŚKOm.gr/ŚKO w gr(błedu)

Femp= 7,67/0,1036=74,035 F_;k-1;N-k=F_0,05;3;193=2,7 Femp> F Odrzucamy Ho

Istnieje różnica między ilością czasu poświęconego na dokształcanie w zależności od miejsca zamieszkania

S2=S1-86, So-(S1-86)=166, So-S1-86=166/-86, So-S1=166-86=80

30. Co to jest szereg rozdzielczy, jakie są jego rodzaje i jak nazywają się ich wykresy.

Szereg rozdzielczy jest statystycznym sposobem prezentacji rozkładu empirycznego. Uzyskuje się go dzieląc dane statystyczne na pewne kategorie i podając liczebność lub częstość zbiorów danych przypadających na każdą z tych kategorii.

C^k_n  p^k  q^nk

1 (x_i  EX)³pi / D³X

Szeregi rozdzielcze:

strukturalny (cecha jakościowa, grupowanie typologiczne) punktowy (cecha ilościowa, skokowa)

przedziałowy (cecha ilościowa, ciagła)

punktowy plus przedziałowy (grupowanie wariancyjne)

Wykresem szeregu rozdzielczego jest histogram. (liczebności, częstości).

31.Weryfikując Ho: p=po dwustronnej hipotezy alternatywnej otrzymano uemp=1,58 (-1,43, 1,6). Dla jakiego najmniejszego poziomu istotności można w tych warunkach odrzucić hipotezę zerową.

(prawostronnej u emp=1,38)

Uemp=1,58 F(z=0,94295) (dwustronnej) Alfa=1-F(z)=0,05705

Ualfa<Uemp żeby odrzucić

(jednostronnej) Ualfa=1-alfa/2 Alfa=2*(1-Ualfa)

Ualfa dla 1,58=0,94294 2*(1-0,94294)=0,11411 Alfa<0,11411

Weryfikując H₀: p=p₀ przy prawostronnej hipotezie alternatywnej otrzymano u_emp=1,53. la jakiego najmniejszego poziomu istotności można w tych warunkach odrzucić H₀?

Przy poziomie istotności 0,07 1,53ε <1,48 ; ∞)

31.Weryfikując Ho:p=po przy lewostronnej hipotezie alternatywnej otrzymano Uemp=-1,73.Dla jakiego najniższego poziomu istotności mozna w tych warunkach otrzymać H0.

P(x<50)=F(50)=F((50-62)/10)=F(-1,2)=1-0,8849(wartość z tablic)=0,1151

P(50<x<70)=F(70)–F(50)=F((70-50)/10)-0,1151=0,9772-0,1151=0,8621

P(x>70)=1-F(70)=1-0,9772=0,0228

Przedsiębiorca a) x*40=40x (gdzie x to ilość jaj)

Przedsiębiorca b) 0,1151x*35+0,8621x*40+0,0228x+50=39,6525x

Wyszło mi, że to pierwszy producent zarabia więcej

32.Jeżeli zmienna losowa X ma rozkład normalny o parametrach (17;8) a ẋ25jest średnia arytmetyczna próby o liczebności 25 sztuk, to jaki rozkład i o jakich parametrach ma wyrażenie 2 ẋ25+3

X ..N(17:8)

n =25 średnia ..N(17:8/pierw z n) (17:1,6) 2_śre25+3…N(2*17+3:2*1,6) N(37:3,2)

33. Zmienna losowa X ma rozkład normalny o parametrach (10,1). Znaleźć parametry rozkładu zmiennych Z i Y jeżeli wiadomo że Z=2X Y=Z+3

X..N(10:1) Z…N(17:2) Y..N(73:8)

33. Załóżmy ze dla cechy o rozkładzie normalnym proporcja odchylenia standardowego w próbie i zakładanego dla populacji jest jak 1:0,75. Jak liczna musi być próba aby na poziomie istotności 0,05 przy prawostronnej H1 odrzucić hipotezę o wariancji.

33. Co to są liniowe modele mieszane? Podać przykład

34. W sklepie jest 5 szaf, liczba klientów EX=3. Jakie jest prawdopodobieństwo że zabraknie szaf

K=3 EX=3=lambda z rozkła Poissona od k=0 do k=5 odczytuje wartości i je sumuje, następnie 1- suma=prawdopodobieństwo

37. Stwierdzono że w firmie A zarabia się średnio 9 tys., a w firmie B natomiast 12 tyś zł. W obydwu firmach odchylenia standardowe są jednakowe równe 4 tyś. Jaką pensję ma osoba która może być uznana za typową dla obydwu firm jednocześnie.

Odp 10,5

37. 3 fabryki, w proporcjach 1:2:2, prawdopodobieństwo 0,1:0,3:0,4.

(1/2*0,1)+(2/5*0,3)+(2/5*0,4)=0,2*0,1+0,4*0,3+0,02+0,12+0,16=0,3 1+2+2 =5 2/5= 0.4

0.4 x 0.3 = 0.12

Prawdopodobieństwo 12%

Zmienna losowa- f.w której każdej wart. X odpowiada pewien podzbiór zbioru omega, będący zdarzeniem losowym ( ma wartości i ich P). Wyróżniamy: skokową- gdy zbiór wart.zmiennej jest skończony lub niesk.ale przeliczalny; ciągła- nieprzeliczalny(jest przedziałem lub sumą przedziałów)

Funkcja prawdopod.zmiennej losowej- (f.przyporządk.każdej wart zm.los.x P wystapienia) f.rozkładu P- dla skokowej [f(xi)=P(X=x_i)=p_i] f.gęstości- dla skokowej.

Własności: -jest ograniczona (0f(x) 1 sk.; f(x)0 ciąg.); -Suma wszystkich wart=1

Dystrybuanta: f. Która określa P, że wart.zm.los. nie przekroczą arg f: F(x0)=F(X=x0)=P(Xx₀),f.kumulująca P.| Jest: -określona dla R\; -ograniczona od 0 do1; - niemalejąca; -przynajmniej prawostronnie ciągła.

Parametry zm.los: EX- wart.oczek.-wyznacza poł.najbardziej prawdop.wartości zm.los (suma xi*pi-skok., całka x*f(x)dx-ciąg.)

D²X= wariancja- miara rozrzutu wart.zm.los. wokół EX (suma x_i²p_i-EX²-skok.; całka x²f(x)dx-EX²-ciag.); DX- odch.stand.= pierw. z wariancji-wsk.przecietne odchylenie zm od EX; wskaźnik zmienności V=(DX/EX)*100%-służy do porównania zróżnic.zmiennych los.;Stadaryzacja: U=X-EX/DX-jest to przekszt.zm.losowej, w celu uzyskania zm.los.o wart.oczek=0 i wariancji=1.[możemy sprowadzić zm.los.o różnym przecietnym poziomie EX czy stopniu zróżnicowania DX do zm.o jednakoiwych parametrach] kwantyle; wart.modalna wartzm.los.x dla której f.gęstości przyjmuje max.lokalne ;

wsp.asymetrii(skońności)

Dla rozk.jednomodalnych =(EX-Mo)/DX

ROZKŁADY ZMIENNYCH SKOKOWYCH:

ROZKŁĄD DWUPUNKTOWY: zm.los.ma tylko 2 wartości- 1 z prawdop p i 0 z prawd.1-p; EX=p D2X=p(1-p)- stan zdrowia,płeć, przezywalnosc,rogatosc. BERNOULLIEGO (dwumianowy): nieduża, skończona lb el.; wysokie P sukcesu(>0,1);jest symetryczny gdy p=0,5; EX=N*p; D²X= N*p*q; q=1-p

P(x_i=k)=

Jest sumą n zmiennych zero-jedynkowych [przykłąd- siła kiełkowania nasion]

POISSONA: rozkł.graniczny w ciągu zm.los. mających rozkł dwumianowy. Wraz ze wzrostem dł.serii(n) maleje p sukcesu

_x  t _ *

 (=n*p)

Lb.nie jest podana, lub jest b.duża/nieskończ., P sukcesu b.małe; wart.oczek.jest jednocześnie wariancją EX iD²X= przykłądy: lb wypadków, lb.bakterii, zachorowan,awarii w czasie

P(x_i=k)= ^_k!^k  e^ ; e= 2,7182 |||

GEOMETRYCZNY: realizuje się w ciągu niezależnych doświadczeń, które powtarzane są tak długo, aż pojawi sie sukces z prawdop. „p”.Seria składa się z k+1 dośw.w tym k porażek i 1 sukces. Gdy k=0

->sukces pojawia się po 1 dośw. P_p(k)=(1-p)k*p, EX=(1-p)/p; D²X=(1-p)/p²

ROZKŁ.ZMIENNYCH CIĄGŁYCH

NORMALNY: tworzy krzywą dzwonową(gaussa-jej kszt.zalezy od sr.i odchylenia), Własności: -określony dla R\, -symetryczny, oś symetrii przez środek na osi

(x)

y, prosta x=m (m=Mo=Me), rozkł.jednomodalny(1max) a ta wart jest jednocześnie średnią i środkiem wykresu xi=

1

 e 2^2

; parametry: m,

(średnia [„  ’]

 

2

odch.st); X~N(m;sigma); -prawdop.wyst wart zm.los. w przedziałach lb.o konczach wyzn.przez parametry rozkładu jest jednakowe dla każdej zm.o rozkł.norm-regula 3 sigm [ m  -przedział typowy 68%, 2sigma-95%; 3-99,8%, reszta to 0,1%

|||parametry rozkł.standaryzowanego: 0 i 1; jeżeli inaczej należy przenieść punkt: U(lubZ)=	xi  m	(gdy ujemna, to wart odjąć od 1);
	

T-STUDENTA: też symetr.ale bardziej płaski, może zamienić się w normalny gdy opisuje b.liczne populacje ale zwykle są mniej liczne; wartości na osi x to nie parametry tylko średnie z kolejnych pomiarów

Miary położenia: średnia(klasyczna), kwantyle, moda(pozycyjne). Mediana to kwantyl ½. Kwantyle dzielą obs.na częsci, każda cz. to rząd kw.(kwartyl, decyl, centyl)

Miary rozproszenia: klasyczne:wariancja (S²), odchylenie stand. (S), klasyczny współcz. zmienności (V_zk=odch./śr.)-[mówi ile % średniej stanowi odch.stand); pozycyjne: odchyl.ćwiartkowe Q, wsk.zmienności pozycyjny V_ZQ

Dla próby<-> w populacji: x(srednia)-EX(wart.oczekiw); Me(Q_0,01...Q₁)

k	k	^2  p ]-EX^2
S^2, S- war i odch- DX^2, DX; EX=  xi  p ; D^2X= [  xi
i1	i1

ZM.LOSOWA DWUWYMIAROWA: połączenie 2 zm.los.jednowym.określonych na tym samym zbiorze omega. F rozkładu prawdop(gęstości) takiej zm.jest dwuargumentową f. zdefiniowaną: f(x.y)=p_ij=P((X=x_i)”i”(Y=y_j)) -skok., dystrybuanta F(x,y)=P((Xx)”i”(Yy)); rozkłady brzegowe (rozkł.każdej zmiennej): f(x)=P(X=x_i)=p_i=suma p_ij; (tak samo dla Y j) –skok; f(x)=całka f(x,y)dy;...(x,y)dx -ciąg.[funkcje brzegowe rozkładu uzyskuje się przez sumowanie f.rozkładu dwuwymiarowego ze wzgle ja 1 zmienną, prawdop.:

P(x1<X<x2 „i” y1<Y<y2)=F(x2,y2)-F(x2,y1)-Fx2,y2)+F(x1,y1); parametry: wart.oczek obu zmiennych (EX i EY), wariancje obliczane z f.rozkł.brzegowych (D²X,D²Y). Miarą charakteryzującą współzmienność X iY jest kowariancja CXY=suma (xi-EX)*(yi-EY)*p_ij=suma x_iy_ip_ij-EX*EY. Jeżeli zm.X i Y są niezależne to CXY=0. Niezależność zm. można sformułować jako relację m.funkcjami rozkł dwuwymiarowego a brzegowymi: f(x)*f(y) co dla zm.skok.mozna zapisac p_ij=p_i*p_j Tworzenie zm.los.: zm.los.mozna ze soba łaczyc,znajac par.zmiennych składowych mozna obli par.zm.złoż. Jeżeli zmienna V jest liniową kombinacją X₁ i Y₂ ; V=suma ai*Xi to EV=suma ai*Exi, D²V=suma a_i²*D²X_i+suma 2* a_i*a_j*CX_iX_j; CVX=suma ai *D²X_m

TWIERDZENIA GRANICZNE: Złote tw.Bernoulliego: ze wzrostem lb.przpr.dośw. z których kazde moze zakonczyc sie sukcesem lub porażką, czestosc sukcesu skupia sie wokól stałej równej P sukcesu(p), Moivre’a-Laplace’a: ciąg standaryzowanych dystybuant zm.los.o rozkł.dwum.jest zbieżny do dystr.rozkładu norm. standaryzowanego., Lindenberga-Levy’ego-zmienne, których wart.kształtuja sie pod wpływem złożenia wielkiej lb czynników losowych mają rozkł.norm.

ROZKŁADY STATYSTYK Z PRÓBY

Statystyki z próby to zmienne losowe będące funkcją zmiennych X1,X2...( np. średnia arytm, wariancja,) rozkł.statystyk z próby zależy od rozkładu zm.losowych i wlk.próby. Jeżeli znamyu rozkład statystyki z próby, to można szacować wartości parametrów z populacji. Rozkł stat.z próby w których parametrem jest lb.stopni swobody nazywane są dokładnymi i są wykorzyst.w przypadku małych prób.







-Jeśli zmienna X ma rozkł.norm.to sr.arytm.tez ma r.n.o takim samym „m” i odchyleniu pierw(N) razy mniejszym od odch.zmiennejX xN ~ N





, [po







^N

xN  

standaryzacji:

*

N ~ N(0;1) Jeśli rozkł.zm.los. jest norm. ale zaden parametr nie jest znany wtedy wart sr.arytm. ma rozkład t-Studenta z par 

=N-1 zwanym



lb.st.swobody. Et=0, D²t= /( -2)=N-1/N-3;

-Jeżeli zm.los. ma dowolny rozkład ale próba jest duża to śr. będzie miała r.n. x~N(EX;DX/pierw(N))

Wariancja: Jeżeli zm.los.X ma r.n. to dla dowolnej N-el.próby poniższa statystyka ma rozkł. chi-kwadrat Pearson’a ; rozkład o dodatniej asymetrii, wart oczek. Echi²=  =N-1 (lb.st.swob.) a war D²chi²=2  ; Jeżeli próba jest duża (min 100el) to czestosc empiryczna sukcesu bedzie miała r.n. w~N(p; pierw[(w*(1-w))/N]) PRDZEDZIAŁY: w zm.los.ciągłej. Max lb przedziałów to k 5*logN, , dł przedziału: I=(x_max-x_min)/k

Estymator: T_N parametru populacji  to statystyka z próby(f.elementów próby) która słuzy do oszac.nieznanej wart par. populacji Własności: nieobciążoność: gdy wart.oczek.estymatora =estymowanemu parametrowi, E(T_N)=; zgodnosć: jest stochastycznie zbieżny do szacowanego parametru; efektywność: jest tym efektywniejszy im ma mniejszą wariancję; dostateczność: gdy uwzgl. wszystkie informacje z próby. Przedział ufności przedział w którym znajduje sie estymator P(-t<t<t)=1-; 1-- poziom ufności(miara wiarygodności szac.), dł przedziału –miara precyzji szac.

P(-t<

x  

<t)=1-; P( x  t *

S

   x  t  *

S

)= 1-, Dł przedziału zależy odwrotnie prop.od poziomu istotności (), licz.próby(N), a wprost-od

*

N

S

N

N

odch.stand w próbie(S), zwiększ lb.próby k razy= skrócenie przedziału o „pierw.(k)” Ocena precyzji szacowania: miarą prec.jest wspólcz. wzglednej precyzji

S	, precyzyjne jeśli <10%, jeśli <5%-bardzo prec.

x * N

		(N  1)S^2
Przedz.ufności dla wariancji:	
	P
		^2	
				,
		2

	(N  1)S^2				
 2 							 1   , dla P sukcesu:
				
	^21	
			,	
		2		



w(1  w)





w(1  w) 

P w  u

 p  w  u



 1  

N

N









WERYFIKACJA HIPOTEZ hipoteza- stwierdzenie o parametrach rozkł.lub rozkładzie zmiennej losowej. Podział: -parametryczne (mówiące o parametrach rozkładu) -nieparametryczne(dot.rokł.zm.los.). Inny podział: weryfikowalne (H₀)-do ich sprawdzenia istnieją narzędzia(testy stat.);-nie weryf. (H₁) Etapy weryfikacji: -sform.hipotezy zerowej H₀:=A; -dobranie h.altenat. H1->. H1:A (zaprzeczenie), H1:>lub <A (uzupełnienie); -wybór próby i scharakteryzowanie jej za pomocą parametrów; -dobór testu stat.i obl.jego empirycznej wielkości:(test_emp). Wybór zdeterminowany jest rodzajem H₀ i liczebnością próby; -dobranie poziomu istotn.  i okr.obszaru kryt . Obsz kryt-przedział lub ich suma wyzn.przez wart kryt., pole pod f rozkładu nad obsz kryt =, położenie obsz.kryt.zależy od wybraniej uprzednio H altern.(H₁) Granice: t-stud: dwu:(-∞;-t>suma<t_;+∞), jedno: prawo: <t₂_;∞) lewo (-∞;-t₂ >_; u tak samo, ² i F-sned.-połowa ., wartości dla u: F(u)=1-(/2); -odrzucenie lub nie odrz.H₀ (jeżeli wart. testu należy do obsz.kryt- odrzucamy) Jaki test? dopasowany co H oraz cechy i

	x  0
próby. H dot wart.oczek. cech: H0: EX=EX0, jeżeli cecha ma r.n. to H można zapisać jako H0:=0 i stosuje sie t-Stud. temp=			N , jeśli nie ma r.n. to próba
	S

musi być duża i stos test u_emp (tak samo tylko EX₀ zamiast ₀); H.dot wart.oczek 2 populacji H₀: EX₁=EX₂ Jeśli cecha mam w populacji r.n. to H₀:₁=₂ i stosuje

x  x

(N  1)S ^2  (N

2

 1)S

2

2



1

1



się t-Stud. temp=

1

2

;S...=

1

1

*





 , jeśli cecha nie ma r.n. to pr.musi byc duża i stos.test u, uemp=tak samo tylko na dole zamiast S..->

S

N  N

2

 2

^ N1

N2



x1x2

1





(N 1)S^2

S1^2

S2^2

2

2

2



; H.dot wariancji cechy w populacji H0=

=0

jeśli rozpatrywana cecha ma w pop.r.n., stos się test chi-kw.  emp=

; H dot war.cechy w 2 popul.

N1

N2

 ^2

0

2

2

S ^2

H0=1

=2

, jeśli c.ma r.n. stos się F-Sned. Femp=

1

; H dot wart.prawdop. sukcesu w pop H0:p=p0, można zwer.tylko gdy duża próba(N>100), stos test u,

S2 ^2

uemp=

w  p0

;H dot wart prawd. w 2 pop H0:p1=p2; tylko gdy duże próby, test u, uemp=

w1  w2

, gdzie

m1  m2



N1* N2

w



N

N1  N2

N1 N2

p0 (1  p0 )

w(1  w)

N

N

Hipotezy nieparametryczne: -o zgodności rozkładu z rozkł.rozk. teoretycznym, -o niezależności 2 cech., -o losowości wyboru próby , o zgodności rozkładu z rozkł.rozk. teoretycznym, [np. rozkład grup krwi] r.teoret.pozwala wyzn,.P (p_i.) w każdej klasie-służą do obl.teoret liczebności(p_iN) a te są porówn.z

empirycznymi(ni) test chi-kw: ²emp  ^{k (ni  piN)2}

i1 ^Pi^N

KORELACJA: (DO ZMIENNYCH DWUWYMIAR.) jest miarą zależności korelacyjnej (typu liniowego) zmiennych los. i może mieć wart z przedz <-DX*DY; +DX*DY>, znak kowariancji (CXY) inf.o kierunku zależności. Ponieważ CXY jest wlk.mianowaną, zależną od jedn.X i Y, to miarą współzal. liniowej

2 zm. jest współczynnik korelacji liniowej	^XY ^	CXY	; przyjmuje wart od –1 do 1 (znak inf.o kierunku zależności, wartość o sile) Rodzaje zależności: jesli zm. są
		DX* DY

niezależne to CXY=0 ale nie odwrotnie!, są 2 rodzaje zależności: -Stochastyczna -->rozkłady warunk.1zmiennej na każdym poziomie są takie same-f(x,y)=f(x)*f(y)[wawtedy gdy rozkłądy są różne]; -korelacyjna--> wartości oczek.warunkowych rozkładów są jednakowe; EX/Y₁= EX/Y₂=... [gdy rozkł.są równe] Rozkłady warunkowe: R.war. zm.Y pod warunkiem że X=xi określimy P(Y=y_j/X=x_i)=P_ij/P_i –skok, f(y/x)=f(x,y)/f(x)

Zależność 1 zmiennej od 2: jedna ze zm. jest zm niezależną (argument f.) a druga zależną (wartość f.). Przykładem jest regresja. Regresja I rodzaju-f. przyporządkowująca wart zmiennej niezależnej warunkowe wart.oczek. zm.zależnej, ma postać m(x)=E(Y/X=x_i) -->zal.zm YodX, m(y)=E(X/Y=y_i) -->X od Y Regresja II rodz. f.przeprowadzona wg metody najmniejszych kwadratów-najcz. f.liniowa postaci g(y)=_XY*y+_XY -> zal YodX; _XY= wsp.regresji liniowej,

wyraża wlk.zmiany zmiennej zależnej(Y) przy wzroscie zm.niezal.(X) o jednostkę. Wsp. XY- stała regresji, wykresem jest linia prosta. XY= ^CXY ; XY=EX-

D ² Y

_XY*EY; wsp.determinacji: miara inf.jaką część zm.zależnej można wyjaśnić przy pomocy danej f.regresji. Dla f. regresji I rodz. wsp.oznaczany jest ²_YX lub ²_XY a dla lin.regresji II rodz. przez ²_XY. Dla regresji II rodz. wsp.det. jest taki sam dla każdego kier. zależności: ²_XY=(_XY )²= _XY*_{YX ;} ²_YX

	D^2	(E(Y / X))		D^2 Y  E(D^2 (Y / X))	2	2	2	2
=					; [gdzie : D (E(Y/X)) to wariancje warunkowych wart.oczek.; = (E(Y/X=xi)-EY)		* P(X=xi)= (E(Y/X=xi)) *P(X=xi)-(EY)		] [a
		D^2 Y		D^2 Y

E(D²(Y/X)) są wart. oczek. wariancji rozkładów warunkowych = D²(Y/X=x_i)*P(X=x_i)

Suma wariancji warunkowych wart.oczekiwanych i wart oczekiwanej wariancji warunkowych rozkł.dla każdego kierunku zależności=wariancji zm.zależnej, czyli

D²Y= D2(E(Y/X))+ E(D2(Y/X))

OCENA ZALEŻNOŚCI : cel badania związku m.cechami: stwierdzenie czy istnieje zależność m.cechami, czy jest istotna, ocenić siłę zależności. Rodzaje cech: ^połączenie c.jakościowej lub ilościowej skokowej z dowolną, ^poł.c.ilośc.ciągłej z ilośc.ciągłą. Ad^: jeżeli cecha jest skokowa to poszukujemy

ˆ

ni* nj

ˆ

2

2

(n ij  n ij )

zależn.stochastycznej.| H0:cechy są niezal., H1: zal. , nij- liczebności w tabeli, pi=ni/N, liczebność teoretyczna: n ij 

N

; test:



emp  

ˆ

, cechy są zależne

ij

^n ij

gdy: ^2emp  ^2j(r-1)(k-1) <-z tabel(lb st.swob.  dla kolumn i wierszy), sprawdzić też dla mniejszej ; o sile zależności decyduje wsp. T-Czuprowa

T=

^2emp

, jego wartość <0;1>. Jeśli zrobimy T^2 to jest to wsp.determinacji (czyli x zależy w 5% od y)Ad^a.: poł cechy ilość.ciag z taką samą, gdy obie

N *

(r  1)(k  1)

mają w populacji r.n.: kowariancja

inf. czy jest zależność (0) czy nie ma(=0), znak mówi o kierunku zależności: proporcjonalnej(+), odwrtonie.prop.(-), jej wart w przedziale

<-SxSy;SxSy> ; wsp.korelacji liniowej Pearsona: rxy=

covxy

, inf.o sile i keir.zależności, jego wart w przedziale <-1;1>; istotność zależności: H0:E(rxy)=0

S x * S y

[nieistotna], t-stud: temp=

^rxy

, gdy |temp|t;N-2 to hipoteza zostanie odrzucona[jest istotny]. Liczymy (xi- x ), dla y też, potem to do kwadratu (i jeżeli

1 rxy^2

N  2

podzielimy przez N-1 to bedzie S^2x i S^2y.) a do kowariancji (x- x )*(y- y) podzielić przez N-1, Ad^b połaczenie cechy ilosciowej ciagłej z c.il.ciagłą, gdy

przynajmniej 1 nie ma w populacji r.n.:Współczynnik korelacji Spearmana: rs= 1-

6 di ^2

, gdzie di to różnica rang przypisana wynikowi, takie samo temp do

N(N^2  1)

SSR

SSR

SSR

sprawdzenia istotności Snedecora

Femp.= ^k ^ ^1

SSE



SSR(N  k)

, R^2=



-. -

SSE(k  1)

SST

SSR SSE

N  k

12. Zmienna Z ma rozkład normalny standaryzowany. Obliczyć wartość prawdopodobieństwa P(-0,62<Z<1,45). Po co przeprowadza się standaryzację?

P(-0.62<z<1.45) = F(1.45) - [1-F(0.62)] = 0.92647 - 0.26763 = 0.65884

Standaryzacja ma na celu uzyskanie zmiennej losowej o wartości oczekiwanej równej 0 i odchyleniu standardowym równym 1. Wiedząc, że dla rozkładów normalnych wartości dystrybuanty w punktach wyznaczonych przez parametry rozkładu są równe, można każdy rozkład standaryzować i odszukać potrzebną wartość w tablicach.

13,Załóżmy, że dla cechy o rozkładzie normalnym proporcja odchylenia standardowego w próbie i zakładanego dla populacji jest jak 1:0,8. Wylosowano próbę o liczebności 12 elementów. Czy na poziomie istotności 0,05 przy prawostronnej H₁ można odrzucić hipotezę o wariancji? Czy decyzja ulegnie zmianie, jeśli próba byłaby dwukrotnie większa?

rozkład normalny to X~N(0;1), czyli S2=1, S=1, δ=0.8

x2emp= (12-1)/0.8 = 13.75

13.75 ε <19.675; ∞) nie można odrzucić hipotezy o wariancji

gdyby N=24 x2emp = 28,75

28.75 ε <35.172; ∞) nadal nie można odrzucić hipotezy o wiariancji

14. Czy liniowa funkcja regresji o R²=0,45 jest istotna, jeśli próba liczyła 7 obserwacji?

H0: funkcja jest nieistotna

H1: funkcja jest istotna

Femp = N/k / k-1 x R2/1-R2 = 7-1 / 2-1 x 0.45/1-0.45 = 4,91

Femp ε <5,99; ∞)

Funkcja jest istotna.

15.Stwierdzono, że w firmie A zarabia się średnio 9 tys. zł, a w firmie B 12 tys. zł. Odchylenia standardowe są równe odpowiednio 3,5 i 4 tys. zł. Jaką pensję może mieć osoba uznana za typową dla obu firm jednocześnie.

Po rozrysowaniu tego w formie rozkładów normalnych wynika, że dla firmy A typowa osoba to <5,5;12,5>, dla firmy B <8;16>, osoba typowa dla obu firm to <8;12,5>

16. Jak zmieni się długość przedziału ufności dla wartości oczekiwanej, gdy liczebność wzrośnie dwukrotnie? Jakie inne czynniki i w jaki sposób wpływają na długość przedziału ufności dla prawdopodobieństwa?

Liczebność zwiększyła się 2 razy, czyli k=2, √2 = 1,414, czyli przedział skrócił się 1,414 razy. Zwiekszenie liczebności próby k razy powoduje skrócenie przedziału ufności co najmniej

√k.

Zmianę długości przedziału ufności mozna też uzyskać przez zmianę poziomu istotności (im wiekszy poziom, tym dłuższy przedział).

Długość przedziału jest wprost proporcjonalna do odchylenia standardowego, którego raczej się nie zmienia, bo prowadzi to do utraty reprezentatywności próby.

Wielkość obszaru krytycznego zależy od : poziomu istotności-> im mniejszy tym trudniej odrzucić weryfikowaną hipotezę zerową, tym łatwiej popełnić błąd drugiego rodzaju. Położenie obszaru krytycznego zależy od postaci hipotezy alternatywnej.

Jakimi cechami powinny charakteryzować się reszty w analizie regresji? – Powinny mieć rozkład normalny, być losowe, ich wariancja powinna być stabilna.

Jakie są cechy charaktrystyczne dla krzywej Gaussa? K.G. to wykres funkcji gęstości rozkładu normalnego, położenie i kształt zależy od wartości oczekiwanej i odchylenia standardowego, symetryczny względem prostej x=m(=Me=Mo) funkcja gęstości osiąga max dla EX, stąd wartość oczekiwana, mediana i dominanta są równe.

W jakie sposób i po co przeprowadza się standaryzację? Standaryzacja to liniowe przekształcenie w wyniku, którego otrzymujemy zmienną losową o wartości oczekiwanej=0 , odchyleniu standardowym = 1, przeprowadza się ją w celu odczytania z tablic rozkładu normalnego/

Co można powiedzieć o zmienności próby jeśli miary rozrzutu wartości zmiennej mają taką samą wartości ( jaką?) zmienność nie występuje , miary rozrzutu mają wartość 0.

Wymienić cechy jakie powinien posiadać dobry estymator. Nieobciążoność – wartość oczekiwana estymatora jest równa estymowanemu parametrowi E(T_N)= ;Zgodność – estymator jest zgodny gdy jest stochastycznie zbieżny do szacowanego parametru czyli lim PT_N-=1 ;Średnia i mediana SA estymatorami zgodnymi gdyż gdy zwieksza się liczebność próby SA bliskie wartości oczekiwanej; Efektywność-estymator jest najefektywniejszy gdy jego wariancja jest najmniejsza; Dostateczność- gdy estymator uwzględnia wszystkie informacje z próby czyli jest funkcja wszystkich elementów próby

Jaka jest interpretacja współczynnika korelacji i regresji? Jakie wartości mogą przyjmowac te parametry? wsp. korelacji- wskazuje na zależności m. cechami, przyjmuje wartości od –1 do 1. Jeżeli 0 to nie ma zależności, im bliżej –1 lub 1 tym korelacja silniejsza. Znak wskazuje na kierunek zależności, Jeżeli dodatki to proporcjonalna jeżeli ujemny to odwrotnie.Wsp. regresji= przyrost cechy zależnej przypadający na przyrost o jednostkę cechy niezależnej przyjmuje wartości ze zbioru liczb rzeczywistych, a jej znak jest taki sam jak współczynnika korelacji (+/-)

Co to jest histogram i w jaki sposób można go uzyskać? Hitogram to graficzne przedstawienie rozkładu empirycznego cechy. Szereg prostokątów na osi współrzędnych wyznaczonych przez przedziały klasowe , wartości cechy a wysokość, liczebność elementów podziałów. Jest to zestawienie danych statystycznych w postaci wykresu powierzchniowego przylegających do siebie słupków.

Dlaczego w testach istotności nie można przyjmować Ho? Test istotności- teść z rodzaju, w którym na podstawie wyników próby losowej podejmuje się tylko i wyłącznie decyzje odrzucania hipotezy, którą się sprawdza, bądź stwierdza się brak podstaw do odrzucenia jej hipotezy. W teście istotności nie podejmuje się decyzji o przyjęciu sprawdzonej hipotezy, ponieważ bierze się w tym teście pod uwagę błąd pierwszego rodzaju, a jego prawdopodobieństwo to poziom istotności, nie uwzględnia się natomiast konsekwencji popełnienia błędu drugiego rodzaju.

Czym się różnią i jakie maja związek niezależność stochastyczna i korelacyjna? Niezależności stochastyczne występują, kiedy rozkłady warunkowane jednej zmiennej dla wartości drugiej zmiennej są jednakowe. Natomiast mówimy, że zmienne są niezależne korelacyjnie, jeśli, warunkowe wartości oczekiwanej jednej zmiennej są jednakowe dla każdej wartości drugiej zmiennej. Niezależność stochastyczna implikuje niezależność korelacyjną, ale nie odwrotnie.

Jakie są własności dystrybuanty? Ograniczona od 0 do 1 co wynika z def. Prawdopodobieństwa., niemalejąca, co najmniej prawostronnie ciągła, określona dla wszystkich liczb rzeczywistych

Parametry zmiennej losowej: EX- wartość oczekiwana , D²X-wariancja, DX-odch.stand.,inne tj. kwantyle mediana, wartość modlana.

Jakie właśności ma funkcja rozkładu zmiennej losowej? Funkcja F(x) ma własności: jest ograniczona, 0<f(x)<1 dla zmiennej losowej skokowej, F(X)>0 dla zmiennej losowej ciągłej, suma wszystkich wartości funkcji równa się 1.

Własności rozkładu normalnego zmiennej losowej X, każdy rozkład jest jednoznacznie określony przez swoje dwa parametry: wartość oczekiwaną i odchylenie standardowe, rozkład normalny jest symetryczny względem prostej x=u, funkcja gęstościosiaga max dla EX, stad wartość oczekiwana, mediana i dominanta są sobie równe EX=u=Mo-Me. Prawdopod. Występowania wartości zmiennej losowej w przedziałach liczbowych o końcach wyznaczonych przez parametry rozkładu tej zmiennej jest jednakowe dla każdej zmiennej o rozkładzie normalny, Zasada nazywana jest regułą 3 sigm.

Co to jest szereg rozdzielczy jakie są jego rodzaje i jak się nazywają ich wykresy: szereg rozdzielczy jest statystycznym sposobem prezentacji rozkładu empirycznego. Uzyskuje się go dzieląc statystyczne na pewne kategorie i podając liczebność lub częstość zbiorów danych przypadających na każdą z tych kategorii. Szeregi rozdzielcze: strukturalny (cecha jakościowa, grupowanie typologiczne) punktowy (cecha ilościowa, skokowa), przedziałowy ( cecha ilościowa, ciągła), punktowy plus przedziałowy (grupowanie wariancyjne). Wykresem szeregu rozdzielczego jest histogram (liczebności, częstości).

Rozkład empiryczny cechy.

Podstawą do jakichkolwiek analiz statystycznych badanej cechy jest określenie tzw. empirycznego rozkładu cechy. Polega ono na uporządkowanym, uszeregowanym rosnąco wartościom, przyjmowanym przez tę cechę odpowiednio zdefiniowanych częstości ich występowania.

Podać definicję i opisać właściwości funkcji rozkładu zmiennej losowej oraz dystrybuanty.

Funkcje rozkładu zmiennej losowej: przyporządkowuje wartościom tej zmiennej losowej wartości prawdopodobieństw, z jakimi one występują, suma tych prawd. równa się 1. Własności D=R; f=<0;1> jest ograniczona. Zmienna losowa X jest typu skokowego, jeśli może przyjmować skończoną lub nieskończoną, ale przeliczoną liczbę wartości. Zmienna losowa X jest typu ciągłego, jeśli możliwe wartości należą do przedziału ze zbioru liczb rzeczywistych.

F. dystrybuanty: przyporządkowuje wartościom zmiennej losowej wartości prawdopodobieństwa tego ze wartości zmiennej losowej. Przyjmuje wartość nie większą od wartości argumentu, własność jest ograniczona 0<=F(x)

Od czego zależy wartość i położenie obszaru krytycznego?

Wielkość od wielkości wartości krytycznej (U_), a odchylenie od wielkości poziomu istotności , im większe  tym mniejszy obszar krytyczny. Położenie od stosowanego testu zgodności, np. przy rozkładzie normalnym jest dwustronny, a przy rozkładzie  prawostronny. Położenie zależy też od rodzaju weryfikowanej hipotezy – lewostronnej, prawostronnej i obustronnej.

Wypisz hipotezy, które można weryfikować testem T-studenta. Jakie założenia należy przyjąć o populacjach generalnych?

Ho: µ = µ₀ – populacja ma rozkład normalny o nieznanych parametrach, mała próba ,Ho: µ₁ = µ₂ – mała próba, wariancje jednakowe

Omówić definicję prawdopodobieństwa.

1. klasyczna – prawdopodobieństwo zdarzenia A jest to stosunek zdarzeń sprzyjających temu zdarzeniu, do ilości wszystkich zdarzeń elementarnych.

2. aksjomatyczna – niech  będzie daną przestrzenią zdarzeń elementarnych. Jeżeli każdemu zdarzeniu A przestrzeni  zostanie przyporządkowana dokładnie jedna liczba P(A) spełniająca warunki P(A)≥0; P()=1 dla każdej pary wyłączających się zdarzeń A,B P(AB)=P(A)+P(B) to mówimy, że na zdarzeniach

przestrzeni  zostało określone prawdopodobieństwo zdarzenia A, warunki nazywamy aksjomatami

^statystyczna – jeżeli przy wielorakiej realizacji doświadczeń w wyniku których może wystąpić zdarzenie A, częstość tego zdarzenia wyraża wyraźnie prawidłowość, oscyluje wokół pewnej nieznanej liczby, jeżeli wahania częstotliwości przejawiają tendencję malejącą w miarę wzrostu liczby doświadczeń, to liczba P nazywa się prawdopodobieństwem zdarzenia A.

Rozkład Bernoulliego

Zmienna losowa ma rozkład dwumianowy, jeśli przyjmuje wartości k = 0,1,2...n z prawdopodobieństwem określonym wzorem. Parametrem tego rozkładu jest n - liczba doświadczeń, p - prawdopodobieństwo sukcesu. Rezultatem doświadczenia może być A - sukces lub A’ - porażka. Doświadczenie

to powtarzamy wielokrotnie (n) tak, że prawdopodobieństwo sukcesu pozostaje w pojedynczych próbach stałe i równe p. Liczba zaobserwowanych sukcesów to k=0,1,2,...,n EX - np. D²X - np.(1-p)

Jakie dwa rodzaje błędów grożą przy weryfikacji hipotezy?

=Jeśli H₀ odrzucamy, jesteśmy narażeni na błąd I - go rodzaju polegający na odrzuceniu hipotezy prawdziwej wyrażony przez  poziom istotności

=Jeśli H₀ nie odrzucamy, narażeni jesteśmy na błąd II - go rodzaju, który polega na nie odrzuceniu hipotezy fałszywej

16. Na podstawie poniższych danych oblicz średnią ogólną w próbie oraz średnie w poszczególnych grupach

	1	2	5	6	3		7
X^T	6						2
	2	2	0	0	0	X	1
X						T	3
	5	0	5	0	0	Y	2
							0
	6	0	0	6	0		2
							7
	3	0	0	0	3		1
							2

X=72/16=4,5

X₁= 13/2=6,5 X₂=20/5=4

X₄= 12/3=4

17. Przeprowadzone wśród 80 małżeństw badania dotyczące liczby dzieci dostarczyły następujących informacji. Okazało się, że 15% ogółu par było bezdzietnych, 80% miało nie więcej niż 1 dziecko, a 95% co najwyżej 2 dzieci. Maksymalną wartością uzyskaną w tej próbie było 3 dzieci. Czy przeciętna liczba dzieci w tej grupie małżeństw przekracza liczbę 1,2?

N=80 15%=0; 80%≤1; 95%≤2

x	0	1	2	3
ni	12	52	12	4

Średnie x= 1,1= (12*0+52*1+2*12+3*4)/80=88/80

H₀:Ex=1

H₁:EX>1

Uemp.= 1,1-1/0,70*√80= 0²*12+1²*52+2²*12+3²*4=51+48+36=136

S²=1/79 *(136-7744/80)=1/79*(136-96,8)=0,5=0,496

S=√0,496=0,70

Na podstawie próby nie możemy twierdzić, że liczba dzieci jest większa od 1.

52.Dwie osoby wyznaczyły sobie godzinę spotkania między 9 a 10(11). Każda z nich może pojawić się o dowolnej porze i będzie czekać dokładnie 20 min. Jakie jest prawdopodobieństwo, że osoby się spotkają?

Pole trójkąta= 1,2*a*h=1/2*2/3*2/3=2/9

P= 1-2*pole trójkąta=1-2*2/9=5/9=0,56 1-(2/9+2/9) =5/9

Treść z godziną 11 = 11/36

57. czy przedział ufności dla prawdopodobieństwa P(0,35<p<0,47)=0,96 jest precyzyjny? P(0,35<p<0,47)=0,96

(½*0,12/0,41)*100%= 14,63% nie precyzyjny

15.Współczynnik zbieżności cech X i Y wynosi 0,25. Wiadomo, że próba liczyła 200 osobników. Czy zależność między cechami jest istotna? rxy= 0,25 N=100

temp.= rxy/√(1-rxy²)/(N-2)

temp. = 0,25/ √(1-0,25²)/(100-2)=0,25/√1-0,0625/98=0,25/√0,9375/98=0,25/0,0978=0,2556

α z tablic α_=0,05=2,365 α_=0,01= 2,626 2,556>2,365

Odp. Jest istotny ale r2 jest wysoki. Dopasowanie modelu jest tym lepsze im wartość r2 jest bliższa 0.