1. Linie wpływowe – definicja

2. Linie wpływowe sił – metoda statyczna, konstrukcje wyznaczalne,

procedura obliczeniowa.

3. Wzajemność reakcji i przemieszczeń – zasada Rayleigh.

4. Wzajemność przemieszczeń – twierdzenie Maxwella.

5. Linie wpływowe wielkości statycznych – metoda kinematyczna,

konstrukcje wyznaczalne,

procedura obliczeniowa.

6. Linie wpływowe przemieszczeń – metoda kinematyczna,

konstrukcje wyznaczalne, procedura

obliczeniowa.

7. Wyznaczanie wielkości statycznych za pomocą wykresów linii

wpływowych, układy statycznie

wyznaczalne.

8. Obwiednia momentu zginającego.

9. Kratownica, definicja, załozenia kształtowania kratownic.

10. Metody wyznaczania sił w prętach kratownic.

11. Stopnie swobody w układzie dwuwymiarowym.

12. Zmienność geometryczna układu.

13. Zmienność chwilowa układu.

14. Przemieszczenia węzłów konstrukcji. Wzór Maxwella – Mohra.

15. Więzy warunkowo i bezwarunkowo.

16. Wzory określające stopień statycznej niewyznaczalności układu.

17. Własciwosci układów z nadliczbowymi wiezami.

18. Ogólne założenia metody sił.

19. Metoda sił. Obciazenia statyczne.

20. Metoda sił. Obciazenia termiczne.

21. Metoda sił. Obciazenia kinematyczne.

22. Metoda sił. Wpływ sił osiowych.

23. Metoda sił. Podatnosc podpór.

24. Ruszty.

25. Symetria i antysymetria.

26. Ogólne załozenia metody przemieszczen.

27. Stopien kinematycznej niewyznaczalnosci.

28. Plan odkształcen łancucha kinematycznego.

29. Wykresy podstawowe metody przemieszczen.

30. Metoda przemieszczen. Obciazen termiczne.

31. Metoda przemieszczen. Obciazenia osiowe.

32. Metoda przemieszczen. Podatnosc podpór.

33. Linie wpływowe sił – konstrukcje niewyznaczalne. Metoda

statyczna, procedura obliczeniowa.

34. Linie wpływowe sił – konstrukcje niewyznaczalne. Metoda

kinematyczna, procedura

obliczeniowa.

35. Linie wpływowe przemieszczen – konstrukcje niewyznaczalne.

Metoda kinematyczna, procedura

obliczeniowa.

36. Metoda Crossa. Ogólne załozenia, współczynniki wejsciowe,

procedura obliczeniowa.

37. Teoria II rzedu.

38. Równanie rózniczkowe preta sciskanego sił osiowa oraz jego

rozwiazanie.

39. Siła krytyczna.

40. Wzory transformacyjne do obliczenia momentów wezłowych w

pretach sciskanych osiowo.

41. Równanie układu drgajacego o 1 stopniu swobody oraz jego

rozwiazanie.

42. Wzór Geigera.

43. Równanie układu drgajacego o 1 stopniu swobody poddanego

działaniu obciazen wymuszajacych.

44. Równanie tłumionego układu drgajacego o 1 stopniu swobody

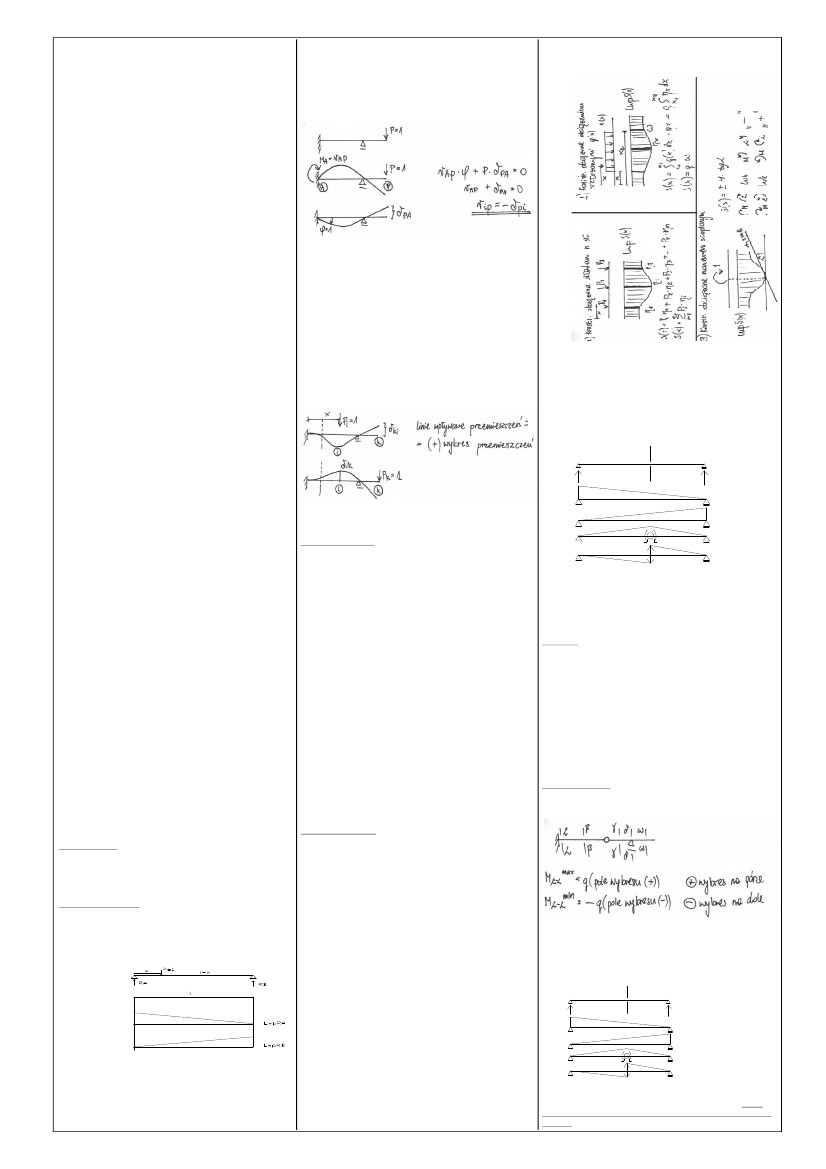
oraz jego rozwiązanie.

Jeżeli siła znajdzie się po prawej stronie przekroju to rozpatrując

wartość równowagi dla lewej części belki otrzymujemy

T α- αP = RB = x/l

Związek ten jest słuszny dla x>0.

7. Wyznaczanie wielkości statycznych za pomocą

wykresów linii wpływowych, układy statycznie

wyznaczalne.

3. Wzajemność reakcji i przemieszczeń – zasada

Rayleigh.

Układ sprężysty obciążony siłą P:

Zależność można sformułować następująco: reakcja węzła „i” układu

sprężystego, spowodowana działaniem siły uogólnionej równej

jedności jest równa co do wartości bezwzględnej, lecz odwrotna co

do znaku- przemieszczeniu na kierunku działania powyższej siły

spowodowanemu przemieszczeniem o jedność wzdłuż linii działania

reakcji więzu „i”. Gdy siła P=1 przemieszcza się po konstrukcji

zachowując nie zmienny kierunek to zbiór wartości rIp przedstawia

linię wpływową reakcji więzu „i”. Linia wpływowa dowolnej siły

pokrywa się z wykresem przemieszczeń wywołanych jednostkowym

przemieszczeniem wzdłuż kierunku działania odpowiedniego więzu.

4. Wzajemność przemieszczeń – twierdzenie

Maxwella.

Przemieszczenie δik odpowiadające i-tej sile (w kierunku tej siły) i

wywołane działaniem siły Pk=1, równe jest przemieszczeniu δki,

odpowiadającemu k-tej sile i wywołanemu przez działanie

jednostkowej siły Pi=1

Styczna poprowadzona w punkcie przyłożenia momentu M do

wykresu lwpS(x).

Takie same zwroty momentu i kąta nachylenia stycznej: + we wzorze

Przeciwne zwroty: - we wzorze

Linie wpływowe można budować 2 metodami:

- metodą statyczną (równania równowagi)//pyt. 2

- metodą kinematyczną (odkształcenia):// pyt. 5 i 6

(tu ze ściągi z worda, nie wiem, czy to dobrze): Liczymy wielkości

statyczne RA , RB , Mα-α , T α-α

a-a

Ra

a-a

Rb

lwpRa

5. Linie wpływowe wielkości statycznych –

metoda kinematyczna, konstrukcje wyznaczalne,

procedura obliczeniowa

Metoda kinematyczna – polega na sporządzeniu linii wpływowych

przemieszczeń wg zasady wzajemności przemieszczeń w układzie

sprężystym.

Sposób kinematyczny sporządzania linii wpływu wielkości

statycznych polega na wykorzystaniu twierdzenia o wzajemności

reakcji i przemieszczeń (tw. Reyleigha) które brzmi: Reakcja rji w

punkcie „j” wywołana siłą jednostkową działającą w punkcie „i” jest

równa co do wartości i różna co do znaku przemieszczeniu δij w

punkcie i na kierunku działania siły wywołanemu przemieszczeniem

jednostkowym zdanym w punkcie j na kierunku reakcji. rji=- δij

Tok postępowaniu przy budowie linii wpływowych sił na podstawie

zasady wzajemności reakcji i przemieszczeń dla dowolnego układu

sprężystego możemy w skrócie ująć w następujących punktach:

a)zwalniamy więź warunkujący występowanie tej siły, której linię

wpływową budujemy;

b) wykonujemy (wymuszamy) przemieszczenie o jedność na

kierunku działania odrzuconego więzu;

c)wykres przemieszczeń (ściślej rzutów przemieszczeń na kierunki

działania obciążenia — zwykle pionowego lub poziomego) punktów

rozpatrywanej konstrukcji, w których może być przyłożone

obciążenie, traktujemy jako poszukiwaną linię wpływową .

d) Znaki rzędnych ustalamy zgodnie z zasadą Rayleigh’a : rip = —

δpi.

lwpRb

lwpMa-a

lwpTa-a

8. Obwiednia momentu zginającego.

Mając wartości wielkości statycznych każdego rozpatrywanego

przekroju konstrukcji, możemy wybrać spośród nich ekstremalne

wartości dla każdego przekroju i sporządzić na tej podstawie

obwiednię danej wielkości.

Obwiednia – obszar, w którym mieszczą się wykresy możliwych

wartości danych wielkości Q ograniczone dwiema liniami.

Wizualizuje jaka może być największa wartość momentów po stronie

włókien górnych jak i dolnych.

(Dysponowanie wartościami wielkości statycznej dla każdego

rozpatrywanego przekroju (punktu) konstrukcji umożliwia wybór

spośród nich ekstremalnych wartości dla każdego miejsca i

sporządzenie na tej podstawie tzw. obwiedni danej wielkości. Jest to

wykres w postaci dwu linii ograniczających obszar, w którym

mieszczą się wykresy możliwe ( dla rozpatrywanych wariantów

obciążenia) wartości danej wielkości Q. Odciętymi tego wykresu są

odcięte kolejnych rozpatrywanych punktów (przekrojów) konstrukcji,

rzędnymi – wspomniane wartości ekstremalne)

Procedura działania:

• zaznaczamy przekroje na belce, dla których obliczane będą wartości

maksymalnych momentów zginających w wyniku obciążenia belki

obciążeniem ciągłym o natężeniu q.

1. Linie wpływowe – definicja

Jest to wykres przedstawiający zależność pomiędzy wartością pewnej

wielkości statycznej a położeniem obciążenia statycznego

(skupionego, ciągłego, momentu), wywołującego tę wartość. Służy

do określania wielkości sił wewnętrznych lub przemieszczeń pod

wpływem dowolnego obciążenia jednostkowego, w dowolnym

przekroju.

2. Linie wpływowe sił – metoda statyczna,

konstrukcje wyznaczalne, procedura

obliczeniowa.

Aby określić linię wpływową wielkości statycznej układamy

równanie wielkości statycznej S z funkcji x. S=f(x). X- określa

położenie siły P=1 na konstrukcji.

Metoda statyczna – polega na określeniu danej wielkości w sposób

analityczny i oparty na równaniach statycznych. Dla uproszczenia

zapisu w równaniach określających rzędne linii wpływowych

dodolnych wielkości S, stosuje się uproszczenie:

S=…. zamiast ηs=….; Ra=……., zamiast ηRa = …..

Procedura obliczeniowa

• reakcja podporowa: Siłę P =1 ustawiamy w dowolnej odległości , x

od podpory A. Z równania ∑MB=0 znajdujemy RA *l – P*(l-x)=0 .

Podstawiając x=0 otrzymujemy RA=1, analogicznie postępujemy

przy linii wpływowej równej RB, tylko korzystamy z równania

∑MA=0

6. Linie wpływowe przemieszczeń – metoda

kinematyczna, konstrukcje wyznaczalne,

procedura obliczeniowa.

Metoda kinematyczna – polega na sporządzeniu linii wpływowych

przemieszczeń wg zasady wzajemności przemieszczeń w układzie

sprężystym.

Sposób kinematyczny sporządzania linii wpływu wielkości

statycznych polega na wykorzystaniu twierdzenia o wzajemności

reakcji i przemieszczeń (tw. Reyleigha) które brzmi: Reakcja rji w

punkcie „j” wywołana siłą jednostkową działającą w punkcie „i” jest

równa co do wartości i różna co do znaku przemieszczeniu δij w

punkcie i na kierunku działania siły wywołanemu przemieszczeniem

jednostkowym zdanym w punkcie j na kierunku reakcji. rji=- δij

Tok postępowania:

1) obciążamy konstrukcję reakcją R=1 lub momentem M=1 na

kierunku przemieszczenia, dla którego lwp jest sporządzana

2) rysujemy wykres przemieszczeń reakcji R=1 lub M=1. Otrzymany

wykres jest linią wpływową przemieszczenia.

• Im więcej przekrojów, tym dokładniejszą obwiednię otrzymamy.

Standardowo przekroje robimy w podporach i w połowie długości

przęseł. Nie robimy w przegubach, gdyż moment w przegubie jest

=0.

• W zaznaczonych przekrojach rysujemy linie wpływowe momentów

• obliczamy wartości momentów maksymalnych i minimalnych w

każdym z przekrojów:

a-a

Ra

a-a

Rb

lwpRa

lwpRb

• Siła poprzeczna Tα-α

Gdy siła znajduje się na lewo od przekroju α-α to ∑Y=0 dla prawej

strony i otrzymujemy równanie:

T α- α L = RA – P = –x/l = -RB

Jest to równanie jednej gałęzi linii wpływowej prawdziwe dla x<a.

Podstawiając x=0, x=1 kreślimy część linii wpływu Tα- α tylko z

lewej strony przekroju α- α.

lwpMa-a

lwpTa-a

Ostatecznie na jeden wykres nanosimy wartości maksymalne i

minimalne, wyliczone jak wyżej dla kolejnych przekrojów. Jest to

wykres obwiedni momentów zginających pod działaniem obciążenia

ciągłego.

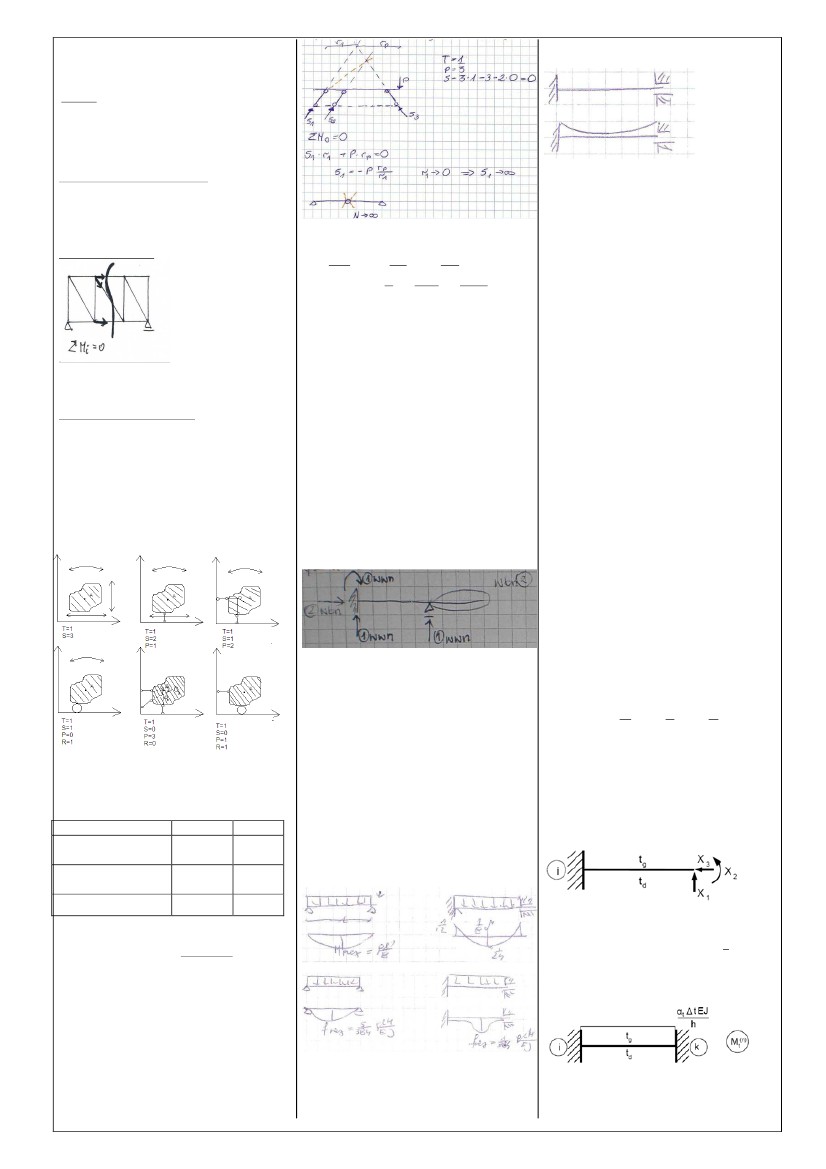
9. Kratownica, definicja, założenia kształtowania

kratownic.

Jest to niezmienny układ prostoliniowych prętów, połączonych ze

sobą w węzłach współśrodkowo przegubami idealnymi (brak tarcia),

przeguby pracują tylko na siły osiowe.

Założenia:

- pręty są prostoliniowe i połączone współśrodkowo w węzłach

- w przegubach nie ma tarcia

- konstrukcja jest niezmienna geometrycznie i chwilowo

- wszystkie obciążenia zewnętrzne oraz ciężar własny przekazywane

są wyłącznie w postaci sił skupionych przyłożonych w węzłach

8) W konstrukcjach statycznie niewyznaczalnych mogą być

realizowane wstępne stany naprężenia, (ale tylko na kierunku więzów

warunkowo niezbędnych)

10. Metody wyznaczania sił w prętach kratownic.

metoda równoważenia węzłów (analityczna):

∑X=0 ; ∑Y=0

Wady metody:

1. kolejność rozwiązywania jest zdeterminowana układem prętów,

2. duża liczba "rachunków"

3. kratownica bez węzła o 2 prętach nie może być "ręcznie"

rozwiązana

metoda Rittera (przekrojów)

14. Przemieszczenia węzłów konstrukcji. Wzór

Maxwella-Mohra.

+ ∫ℕ

= ∫

∙

+ ∫

+ ∫

∆

∙

+

+ ∫

∙

∙ℕ

+

∙

−

∆

9) Liczba możliwych wstępnych stanów samo naprężenia dla danego

rodzaju konstrukcji równa jest stopniowi statycznej

niewyznaczalności

10) Siły w więzach warunkowo niezbędnych są zależne od

sztywności poszczególnych elem. Sztywność: EA- ściskanie i

rozciąganie, EJ- zginanie GA-ścinanie

11) Wszystkie więzy warunkowo niezbędne współpracują w

konstrukcji ze sobą (tzn. działają na jedne które oddziaływają na inne

itd.)

12) W miarę przeciążania konstrukcji mogą pojawić się przeguby

plastyczne powodujące zmniejszenie stopnia statycznej

niewyznaczalności

18. Ogólne założenia metody sił:

Metoda sił jest sposobem rozwiązywania układów statycznie

niewyznaczalnych, czyli układów o nadliczbowych więzach

(zewnętrznych i wewnętrznych). Sprowadza się ona do rozwiązania

układu statycznie wyznaczalnego (układ podstawowy w metodzie sił),

który powstaje z niewyznaczalnego układu rzeczywistego przez

wprowadzenie w miejsce odrzuconych więzów niewiadomych sił. Jest

to prosty sposób na rozwiązanie układów ramowych, kratowych czy

łukowych. W niniejszym rozdziale omówione zostaną ogólne

założenia oraz tok postępowania obliczeniowego w metodzie sił.

Istota metody opiera się na pozbawieniu rozpatrywanego,

obciążonego układu nadliczbowych więzów, dbając jednak przy tym o

to, aby pozostał on geometrycznie niezmienny. W miejsce myślowo

usuniętych więzów wstawiamy niewiadome siły. Następnie, aby

zachować kinematyczną identyczność układu rzeczywistego z nowym,

nazywanym dalej układem podstawowym w metodzie sił, określamy

sumaryczne przemieszczenia po kierunkach działania tych sił.

Ponieważ w rzeczywistości w tych miejscach istniały więzy,

przemieszczenia te są równe zero. Układając te warunki w równania

otrzymujemy wyznaczalny układ, a zatem możemy obliczyć wartości

nadliczbowych niewiadomych.

1) Określamy stopień statycznej niewyznaczalności ns

2) Usuwamy tyle więzów warunkowo niezbędnych (nadliczbowych)

ile wynosi ns tak, aby konstrukcja pozostała układem niezmiennym i

otrzymujemy schemat statycznie wyznaczalny.

3) Układ obciążamy obciążeniem zewnętrznym oraz siłami

jednostkowymi na kierunku usuniętych więzów.

4) Wyznaczamy sumaryczne przemieszczenia (przesunięcia lub

obroty) na kierunkach działania sił nadliczbowych (rysujemy

wykresy momentów i obliczamy δ)

5) Rozwiązujemy układ równań kanonicznych

6) Opracowujemy końcowe wyniki (przemnażamy wykresy

momentów od obc. jednostkowych na kierunkach usuniętych węzłów

podporowych przez wyniki rozwiązań układów równań i sumujemy

je) M=M1 x1+M2 x2+… +MP.

obciążenia statyczne:

(4,5 człon) wpływ obc. termicznych; (6,7) wpływ podpory podatnej;

(8) wpływ obciążenia kinematycznego – przemieszczenia

EJ/EA/GA-sztywność na zginanie/ścikanie(rozciąganie)/ścinanie

M,N,T–siły przekrojowe od obciążeń jednostkowychM, N, T – siły przekrojowe od obc. jednostkowego wstawionego wmiejscu i kierunku w jakim chcemy obl. odkształcenie.

Ri-(6)-siła w podporze podatnej; (8)- siła od obc. jednostkowego na- przecięcie kratownicy przez 3 pręty nie schodzące się w jednym

kierunku reakcjiwęźle

- z równań równowagi: ∑X=0 ; ∑Y=0 ; ∑Mi=0 obliczamy wartości w Mi – moment na podporze podatnej

Ri – siła od obciążenia jednostkowego w podporzeprętach

Mp – moment od obciążenia momentem w podporze

µ- wsp. zależny od kształtu przekroju poprzecznego prętaMetoda Henneberga (wymiana prętów) :

-Polega na usunięciu jednego pręta i wstawieniu go gdzie indziej, ale αt- wsp. rozszerzalności termicznej

t-średnia zmiana temp. w osi prętaw ten sposób, żeby zachowana była nadal geometryczna

∆t-różnica temperaturniezmienność.

k-sprężystość podparcia liniowego-Zabieg ten ma na celu wyłapania więzu, od którego można by było#-podatność podpory sprężyście zamocowanej (1/ #)

rozpocząć obliczenia analityczne.

h-wysokość przekroju poprzecznego pręta-Po przestawieniu jednego pręta należy skorzystać z zasady

superpozycji: najpierw obliczyć całą kratę dla obciążeń zewnętrznych ∆-przemieszczenia

P, zaniedbując siłę x powstałą w wyniku usunięcia pręta, a następnie

obliczyć kratę tylko dla powstałej siły x.15. Więzy warunkowo i bezwarunkowo

11. Stopnie swobody w układzie

dwuwymiarowym.

niezbędne:

Warunkowo niezbędne-czyli takie które możemy usunąć, zachowując

odpowiednie warunki. Siły w więzach warunkowo niezbędnych

zależą od: EA,GA,EJ – sztywność na ściskanie(rozciąganie),

ścinanie, zginanie

Bezwarunkowo niezbędne- więzy których nie wolno usunąć.

19. Metoda sił. Obciążenia statyczne.

16. Wzory określające stopień statycznej

niewyznaczalności (liczbę więzów nadliczbowych

w różnego rodzaju konstrukcjach):

r-reakcje, p-przeguby

p- reakcje podporowe

+pręty, w- węzły

3) dla ram:ns= r-3+3z-p1-2p2-…-npnr-reakcje, z-obszary

zamknięte, p-przeguby (w zalezności od krotności)

T – tarcze; S – stopnie swobody; R – przeguby; P - pręty

1) dla belki:

2) dla kratownicy:

ns= r-3-p

ns= p-2w

-należy obliczyć stopień statyczny niewyznaczalności

-usuwamy węzły warunkowo niezbędne tyle ile jest równy stopień

-obc. siłami jednostkowymi w miejscu usuniętych węzłów

δ11x1+ δ12x2+∆1P=0δ12= δ21

δ21x1+ δ22x2+∆1P=0

Współczynniki δ i ∆ określa się za pomocą wzoru Maxwella –

Mohra.

Wynikowe wartości momentów zginające określa się wzorem

M=M1X1+M2X2+Mp

= ∫

∙

+ ∫

∙

+ ∫

∙ℕ

12.Zmienność geometryczna układu- mechanizm staje

się konstrukcją. Układ jest niezmienny geometrycznie gdy spełniony

jest warunek s=3T-P-2R≤0;T-tarcza,P-pręty,s-stopień swobodny, R-

przegub (za mało więzów podporowych)

UkładNieswobodny

Geometrycznie niezmienny

(węzły nadliczbowe) –S<3

st.niewyznaczalny

Geometrycznie niezmienny

(bez węzłów nadliczbowych) –S=3

st.wyznaczalny

Geometrycznie zmienny -

s>3

mechanizm

ns= -S (s- stopień statycznej niewyznaczalności)

Swobodny

S<0

17. Właściwości układów z nadliczbowymi

więzami

1) Wystarczy jeden wiąz nadliczbowy by konstrukcja stała się

statycznie niewyznaczalna tzn. że nie możemy jej rozwiązać

wykorzystując tylko równania równowagi.

2) Do wyznaczenia sił w więzach bezwarunkowo niezbędnych

wystarczają równania równowagi.

3) Spełnienie wszystkich dowolnych warunków równowagi przez

wszystkie siły występuje w układach statycznie niewyznaczalnych

jest warunkiem koniecznym, ale niewystarczającym dla

prawidłowości rozwiązania.

4) Więzy nadliczbowe redukują ekstremalne wartości sil

wewnętrznych

20. Metoda sił. Obciazenia termiczne.

Przy obliczaniu układów statycznie niewyznaczalnych należy

pamiętać, że obciążenia takie jak temperatura (ogrzanie

równomierne i nierównomierne), osiadanie podpór (liniowe i

kątowe), czy też błędy montażowe wywołują oprócz przemieszczeń

konstrukcji także siły wewnętrzne.

- nierównomierne ogrzanie (oziębienie) pręta,

- nierównomierne oddziaływanie temp. Na pręt

Układ podstawowy dla układu obustronnie utwierdzonego:

S=0

s>0

13.Zmienność chwilowa układu- Następuje gdy ilość

węzłów jest odpowiednia ale są one źle usytuowane.

Konstrukcja ma prawo do chwilowego obrotu. Układ dwóch tarcz

przegubowo połączonych w punkcie B i przymocowanych do ziemi

dwoma nieprzesuwnymi przegubami A. końce prętów AB i BC mogą

się przemieszczać jedynie po okręgach kół o promieniach r i r1 co w

pierwszym przypadku jest niemożliwe ze względu na brak wspólnej

stycznej. W przypadku zaś drugim okręgi o promieniach r i r1 maja

wspólny odcinek toru – styczną w punkcie B. Układy takie noszą

nazwę układów zmiennych chwilowo

RYSUNEK DALEJ--

5) Więzy nadliczbowe redukują ekstremalne wartości przemieszczeń.

Schemat podstawowy uzupełnia układ równań kanonicznych:

δ11x1+ δ12x2+ δ13x3+ δ 1t=0

δ21x1+ δ22x2+ δ23x3+ δ 2t=0

δ31x1+ δ32x2+ δ33x3+ δ 3t=0

∆Wzór Maxwella-Mohra: &'( = ∫ ℕ+ ∫t-średnia zmiana temp. w osi pręta

Wykres momentów w układzie niewyznaczalnym jest po stronie

„zimniejszej”. td>tg

Czyli wykres momentu zginającego dla belki obustronnie

utwierdzonej obciążonej różnicą temperatur ∆t:

6) Układy statycznie niewyznaczalne, obciążone w obszarach

więzów warunkowo niezbędnych z układami samo równoważących

się sił, nie pracują w obszarach więzów bezwarunkowo niezbędnych.

7) Konstrukcje statycznie niewyznaczalne są wrażliwe na obciążenia

kinematyczne lub termiczne (Powstają przemieszczenia i siły

wewnętrzne), ale tylko w obszarach więzów warunkowo

niezbędnych.

21.Metoda sił-obciążenie kinematyczne

Rozwiązując metoda sił konstrukcje obciążoną obciążeniem

kinematycznym należy korzystać z form wzoru Maxwella-Mohra

odpowiednich dla danych współczynników.−∆Ri-siła od obciążenia na kierunku reakcji; ∆-przemiesczenie

Równanie kanoniczne będą sumami przemieszczen na kierunku

nadliczbowych więzów, z tym ze musza uwzględniać

przemieszczenia (δiα), które wystąpiły w układzie podstawowym.

δ11X1+ δ12X2+ δ13X3+…+ δ1nXn+∆i∆=0

MM

dx

EJ

wymnażając odpowiednie pola wykresów przez odpowiednie rzędne,

np.: ä 21 to suma przemnożonych pól z wykresu M1 przez

1)korzystamy z pierwszej cz. wzoru Maxwella-Mohra ∑ ∫

)/

. 0

+, *jest szukaną podatnością.

Posługujemy się też parametrem określanym jako sztywność

podpory. Określamy w taki sposób relację między siłą a ugięciem

podpory. Jest to po prostu odwrotność podatności.

f=

k=

)

2

*

3 4

/

Podstawową cechą łańcucha kinematycznego jest jego ruchliwość.

Posługujemy się równaniami na oś X i Y. Przyjmujemy jedno z

przemieszczeń ∆i=1 i wyliczamy ψi=∆i/l Obliczamy zależności

kątowe w łańcuchu kinematycznym: Σxiψi=0, Σyiψi=0 i wyliczamy

ψi. Wielkości przemieszczeń końców pręta: ∆i=ψili

Jeśli przyłożymy siłę N=1 [N], to wyrażenie przekształci się do

postaci:)

∆) =

+,Wynika z tego, że wyrażenie:

28. Plan odkształceń łańcucha kinematycznego.

odpowiadające im rzędne z pól wykresu M2*1/EJ

2)korzystamy ze wzoru kanonicznego met.sił

ä x + ä x + ∆

 11 1 12 2

1P = 0  podstawiając wartości i tworzącä 21x1 + ä 22 x2 + ∆2 P = 0

układ równań.

wykresu Mi.

24. Ruszty

∆ iP = - ∑ R • ∆ ,gdzie ∑ R to suma reakcji z

29. Wykresy podstawowe metody przemieszczeń.

Zwrot reakcji jest dodatni gdy działa ona zgodnie z założonym

obciążeniem. Dla obc.kinem.Mp=0Rusztem nazywamy konstrukcję składająca się z podłużnic i

poprzecznic. Krzyżujące się pręty są ze sobą połączone za pomocą

przegubów. Obciążenie z podłużnic przenosi się częściowo na skraje

podpory podłużnic, częściowo na dźwigar poprzeczny.

- rozwiązujemy belkę niższą (podłużnicę)

- rozwiązujemy belkę wyższą (poprzecznicę)

3)Rozwiązanie układu daje współczynniki Xi przez które

- rysujemy lwp

wymnażamy wykresy Mi. Suma wkresów daje ostateczny wykres M.

22. Metoda sił. Wpływ sił osiowych

1)Uwzględniamy wpływ sił osiowych zgodnie z wz.Maxwella-Mohra∙∙ℕ

= ∫+ ∫

np.:

wymnażając odpowiednie pola wykresów przez odpowiednie rzędne,

ä 21

to suma przemnożonych pól z wykresu M1 przez

odpowiadające im rzędne z pól wykresu M2*1/EJ+ suma

przemnożonych pól z wykresu N1przez odpowiadające im rzędne z

pól wykresu N2*1/EA.

EJ-sztywność na zginanie wyrażona iloczynem mod. Younga przez

mom.bezwładności,

EA - sztywność na ściskanie-iloczyn mod Younga i pola przekroju

elementu

M, -moment od obciążeń jednostkowychN, ℕ - siły osiowe normalne2)korzystamy ze wzoru kanonicznego met.sił

25. Symetria i antysymetria.

ä11x1 + ä12 x2 + ∆1P = 0 

 podstawiając wartości i tworząc układ

ä 21x1 + ä 22 x2 + ∆ 2 P = 0

równań.

∆ iP =

∑∫

NiNj

dx

EA

3)Rozwiązanie układu daje współczynniki Xi przez które

wymnażamy wykresy Mi.

Suma wkresów daje ostateczny wykres M=Mi*Xi+MP. Aby

ujednolicić jednostki przyjąć EJ=EA*l2

23. Metoda sił. Podatność podpór

Układy takie można rozwiązywać od razu jako całe lub dokonać ich

podziału na dwie odrębne części tj. symetryczna i antysymetryczną.

Siły w prętach dzielimy na symetryczne M,N i anty symetryczne T.

W podporach symetryczna jest siła R natomiast siły antysymetryczne

to M,H Aby utworzyć po przecięciu konstrukcji układ symetryczny

bądź też antysymetryczny należy w miejscu występowania

konkretnych sił ustawić odpowiadające im podpory.

26. Ogólne założenia metody przemieszczeń.

Podpory sprężyste zwane też podporami podatnymi, mogą ulegać

skróceniu lub wydłużeniu pod wpływem działających sił.

Przemieszczenia występujące w tych podporach są wprost

proporcjonalne do reakcji w nich występujących. Podpora może mieć

podatność liniową lub obrotową (kątową). Podpora o podatności

liniowej to na przykład sprężyna pionowo podpierająca belkę.

Podpora o podatności obrotowej to taka, w której pod wpływem siły

nastąpi obrót przekroju. Podatność podpory f to wartość

przemieszczenia wynikająca z działania jednostkowej siły. Podatność

liniową wyrażamy w [m/N], natomiast podatność obrotową w

[rad/Nm]. Jeśli na naszą podporę zadziała siła N (wzdłuż jej osi,

normalna), to zgodnie z prawem Hooke`a, pręt o długości pierwotnej

l ulegnie skróceniu o ∆l.*)

∆) =

+,

Niewiadomymi są: przemieszczenia węzłów. Równania kanoniczne

wyrażają reakcje w miejscu dołożonych więzów (przesuwy i obroty).

O liczbie niewiadomych decyduje stopień kinematycznej

niewyznaczalności (SKN). Jest to liczba więzów, które trzeba

wprowadzić aby układ usztywnić. Momenty zginające i siły tnące

wywołane są obrotami końców pręta oraz przesunięciami

prostopadłymi do osi pręta.

27.Stopień kinematycznej niewyznaczalności.

Liczba niewiadomych metody przemieszczeń; odpowiada liczbie

fikcyjnych węzłów które trzeba wprowadzić, aby zastąpić układ

rzeczywisty układem kinematycznym wyznaczalnym o znanych

przemieszczeniach węzłów np=Σφ+Σ∆, Σφ –łączna liczna obrotów

węzłów sztywnych, łącząca co najmniej 2 statycznie niewyznaczalne

pręty, Σ∆=2w-p-u+d –liczba niezależnych przesunięć (w-węzły, p-

pręty, u-pręty, w których koniec ma swobodę przesuwu prostopadle

do osi pręta, d-przesztywnienia)

30.Metoda

termiczne.

przemieszczeń.

Obciążenia

Obciążenie termiczne wywołuje zmianę długości, ugięcia pręta.

W układach statycznie wyznaczalnych zmiana temp. wywołuje

deformacje i przemieszczenia, ale nie powstają siły wewn. W

ustrojach statycznie niewyznaczalnych wywołane przemieszczenia i

deformacje prowadzą do wystąpienia momentów zginających, siły

poprz. I podł. Siły te mogą być tak duże, że nie powinny być omijane

w obliczeniach. W metodzie przemieszczeń ogranicza się to do

wprowadzenia do równań kanonicznych składnika temp. rit. W obl.

Przyjmuje się, że wraz z wysokością przekroju temp. zmienia się

liniowo:5 = 6

∆

Rodzaje odkształceń:

a)liniowe wydłużenie lub skrócenie pręta∆(: + ∆(;

Ogólny wzór określający, sposób budowy linii wpływowej dowolnej

=7 >?@ A@ęBC>śA@)78 = 9 ∙ ) ∙

2

siły S: lwpS=S1 lwpX1+S2 lwpX2+...+SnlwpXn+lwpSp lub skrócony:

)

lwpS=ΣSilwpXi+lwpSp gdzie: Si –wartość rozpatrywanej siły S w

78 = 9 ∙ E∆(; F + ∆(: FG=7 >H)FIł>śA@ F >H J>H?KL7M)

ℎ

układzie podstawowym pod wpływem Xi=1, lwpXi –linia wpływowa

b)obroty:

nadliczbowej niewiadomej zastępującej nadliczbowy więz i, lwpSp –

NO PNQ∆5= =

linia wpływowa siły S w układzie podstawowym, n –stopień

66))

statycznej niewyznaczalności.

7: = ∆ ∙ K:7; = ∆ ∙ K;∆K = ∆K: − ∆K;

Etapy: -obc. rozpatrywanej belki poruszającą się siłą P=1, skierowana

22∆PR∆PRzgodnie z kierunkiem obciążeń przewidzianych dla danej konstrukcji

5@ = 9 S6 5C = −9 S6 =9 − 7?J. U>B?BFUB. )@V@>7FW)–położenie siły P=1 określamy odciętą x i układamy równanie

Rit Wywołuje: zmianę długości, ugięcia -różnica temperatur: (2

schematy) –ogrzanie (oziębienie) równomierne pręta (4 wyrażające poszukiwaną wartość w funkcji x -linie wpływowe sił

wewnętrznych możemy wyrazić w zależności od linii wpływowych

schematy)36. Metoda Crossa. Ogólne założenia,momentów podporowych –linie wpływową dowolnej wielkości

statycznej: lwpS=ΣSilwpXi+lwpSp gdzie: Si –wartość rozpatrywanejwspółczynniki wejściowe, procedura

siły S w układzie podstawowym pod wpływem Xi=1, lwpXi –liniaobliczeniowa.

wpływowa nadliczbowej niewiadomej zastępującej nadliczbowy więz

Rozwiązujemy układy mające nadliczbowe więzy – statycznie

i, lwpSp –linia wpływowa siły S w układzie podstawowym, n –

niewyznaczalne. Niewiadomymi są momenty zginające wstopień statycznej niewyznaczalności.

przekrojach przywęzłowych, a schemat statyczny tzw. podstawowy

?? t/h?? t/h(zastępczy) przyjmuje się taki sam jak w metodzie przemieszczeń. Po

wyznaczeniu momentów wyjściowych przeprowadza się rachunkowe34. Linie wpływowe sił – konstrukcje

wyrównanie momentów w węzłach drogą kolejnych przybliżeń

niewyznaczalne. Metoda kinematyczna,<- EJαt∆t/h(iterację). Przyjmujemy umowę odniesienie do znaków identyczną,

procedurajak dla metody przemieszczeń. Współczynniki

obliczeniowa.1) sztywność giętna pręta –dla kokardy Sij=4EJ/l –dla trójkąta

Zwalniamy jeden, odpowiedni zew. lub wew. więz i dokonujemy Sij=3EJ/l

?jednostkowego przemieszczenia na kierunku siły, której lwp 2) sztywność węzła Si=ΣSij, Si=Sij+Sik+Sil, Sin=Min/φ, Sin=Min

rysujemy3) rozdzielniki momentów równoważnych czyli stosunek sztywności

Rzędne lwp wielkosci statycznej: ηlwpS= -[MM/EJ dx – R∆]

pręta do sztywności węzła rij=Sij/Si, rik=Sik/Si, ril=Sil/Si, rij+rik+ril=1,

Wykonując linie wpływową:nΣ1rin=1

- reakcji, w postaci siły skupionej lub siły poprzecznej dokonujemy

4) przekaźniki momentów –stosunek momentu przekazanego do

przesunięcia o jedność wzdłuż kierunku działania odpowiedniej siły

- momentu wymuszamy obrót o kąt jednostkowy zgodnie z momentu przekazywanego z przekroju doznającego obrotu

<- ∆t=t αt l

Pij=M(drugi węzeł)/M(gdzie φ)założonym kierunkiem działania tego momentu

Z PRAWEJ STRONY(lewego przykładu) ZAMOCOWANIE

SZTYWNE BEZ REAKCJI W OSI PRĘTA (klocek nad i pod

prętem)

31. Metoda przemieszczen. Obciazenia osiowe.

Obciążenia osiowe są to siły skierowane równolegle do pręta.

Powodują przemieszczenie pręta zgodnie z kierunkiem danej siły, a

razem z nim innych niezablokowanych prętów w konstrukcji. Wpływ

sił podłużnych osiowych (1,2 wykres), +ciężar własny (3 w), bez

wpływu sił osiowych (4 w), z wpływem (5 w)

32. Metoda przemieszczen. Podatnosc podpór.

W konstrukcjach budowlanych występują przypadki sprężystego

osiadania podpór. Wielkość osiadań zależna jest od działającej siły.

Zazwyczaj przyjmuje się liniową zależność wielkości osiadania i siły

(reakcji). Im większa siła tym większe osiadania. Rodzaje

podatności:

a)Podatność podparcia K- siła powodująca jednostkowe

obniżenie podpory

b)Podatność podpory w- obniżenie podpory siłą

jednostkową

Zależność : w=(1:K)

ns=r-3-p (metoda statyczna), rii=ΣMi+κ (moment) gdy Zi to obrót,

rii=ΣMi+k (siła) gdy Zi to przesów

35. Linie wpływowe przemieszczen – konstrukcje 37. Teoria II rzędu.

niewyznaczalne. Metoda kinematyczna,W teorii II rzędu uwzględniamy wpływ narastającego ramienia siły

wyboczeniowej na moment wyboczeniowy.procedura obliczeniowa.

Obciążamy rozpatrywaną, statycznie niewyznaczalną belkę

nieporuszającą sie siłą jednostkową (P=1 lub M=1) działającą wzdłuż

rozpatrywanego przemieszczenia i obliczamy rzędne linii ugięcia

spowodowanego tym obciążeniem, korzystając ze wzoru:

ηlwpV(φ)=Σ∫MM/EJ dx.

Otrzymana linia ugięcia będzie poszukiwaną linią wpływową

przemieszczenia jako linii ugięcia belki obciążonej siłą

nieporuszającąsiębezpotrzebyobliczaniarzędnych.

33. Linie wpływowe sił – konstrukcje

niewyznaczalne. Metoda statyczna, procedura

obliczeniowa.

38. Równanie rózniczkowe preta sciskanego sił

osiowa oraz jego rozwiązanie.

X=

:\ ]

X

M=5) = bc + bS 5 + bd A>?_5 + be ?@V_5 - rozwiązanie

:^ \

+

=

Z

−

Z

:] `_S :^`

−

∙

= 0 - równanie różniczkowe

∙

Y

Z

Y

Z

= −[

39. Siła krytyczna.

Obciążenie dopuszczalne oblicza się ze wzoru:

rZ Y + Z{Y| + Yq = s

Rozwiązanie: Y = }~{ v w=rx + •)

rx = €rZ − {Z

gdzie:

Pkr – obciążenie krytyczne

xw – współczynnik bezpieczeństwa

40. Wzory transformacyjne do obliczenia

momentów wezłowych w pretach sciskanych

osiowo.

1.Belka obustronnie utwierdzona:

f

f

=

=

=

=

g

g

g

g

h =i)j + k=i)jf − l=i)mn

hk=i)j + =i)jf − l=i)mn

h ′=i)j − "=i)mn

h "=i)j n

2.Belka jednostronnie utwierdzona:

h ′=i)j − p′=i)mnf =

g3.‘Wspornik’:

f

f

RYS.

41. Równanie układu drgającego o 1 stopniu

swobody oraz jego rozwiązanie.

Yq + rZ Y = s

r=t

u

Rozwiązanie: Y = v w=r + j)

42. Wzór Geigera

300 1

h=[]

y mm

Y=

x gy

y

43. Równanie układu drgającego o 1 stopniu

swobody poddanego działaniu obciążeń

wymuszających.

rZ Y + Yq =

z= )

u

44. Równanie tłumionego układu drgającego o 1

stopniu swobody oraz jego rozwiązanie.