1.Ekonometria - nauka o mierzeniu zjawisk ekonomicznych ich zależności od innych zjawisk ekonomicznych demograficznych społecznych przyrodniczych itd w celach poznawczych i prognostycznych

2.Klasyczna ekonometria (Lange) - nauka zajmująca się ustalaniem za pomocą metod statystycznych konkretnych. Ilościowych prawidłowości zachodzących w przyrodzie

3.Model ekonometryczny

Według czerwińskiego - model może być rozumiany ogólnie, instucyjnie jako obraz odbicie odwzorowania określanego obiektu w określonym języku

Według bartosiewicz - model ekonometryczny to ustalona statystyczna zależność wyróżnianego bądź wyróżnianych zjawisk ekonometrycznych od zjawisk czynników

4.Formalnie - model ekonometryczny to układ równań lub funkcji na ogół wielu zmiennych przybliżanych z pewną dokładnością opisywany fragment rzeczywistości ekonomicznej zależności zmiennych ekonomicznych od innych zmiennych

5.(ksi)- składnik losowy - to łączny efekt oddziaływania na zmienną y tych wszystkich czynników, które w sposób bezpośredni nie zostały uwzględnione w zbiorze x jest to zmienna losowa w określonym rozkładzie

E(ksi)=0

D^2(ksi)=ro^2

6.Objaśniające - objaśniające kształtowanie się zmiennych endogenicznych same przez model objaśniane nie są (x) wśród nich może być zmienna czasowa „t”

-zmienne opóźnione lub z wyprzedzeniem czasowym

7.Klasyfikacja modeli ekonometrycznych

Według walorów poznawczych

a).przyczynowo - skutkowe - w modelach tych zmienne objaśniające są obiektywnymi przyczynami kształtowania się zmiennych endogenicznych.

b).symptomatyczna - zmienne objaśniające nie reprezentują przyczyn są jedynie silnie skorelowane ze zmienną endogeniczną

c).Tendencji rozwojowych- opisują mechanizm rozwoju badanych zjawisk w czasie. W modelach tych mamy jedynie zmienną czasową t lub pewne jej funkcje

d).autoregrysyjne - modele tego typu, że zmienna endogeniczna jest z dokładnością do składnika losowego wyjaśniania przez własne wartości wzięte z odpowiednimi opóźnieniami czasowymi.

8.Modele wg kryterium uwzględniania czasu

a).dynamiczne - w sposób bezpośredni uwzględniana jest zmienna czasowa albo pośrednio zmienne opóźnione

b).statyczne - czas nie uwzględniony w żaden sposób

9.Etapy budowy modelu

a).sprecyzowanie przedmiotu badania - wybór zjawiska badanego

b).Specyfikacja modelu

-zmienne (praca merytoryczna)

-postać analityczna (analiza merytoryczna i formalna)

c).Zbieranie danych statystycznych

d).Analiza własności wybranych zmiennych (analiza formalna)

-zmienność wartości - zmienne, które nie odznaczają się wystarczającą zmiennością nie dostarczają dostatecznej informacji

-stopień skorelowania z innymi zmiennymi - wybieramy takie zmienne objaśniające, które są silnie skorelowane ze zmienną objaśnianą i słabo skorelowane między sobą

e).Estymacja (szacowanie) parametrów strukturalnych modelu

-model najmniejszych kwadratów

f).Weryfikacja modelu ocenia dokładność opisu badanego zjawiska

g).wykorzystanie modelu np. wnioskowania w przyszłość lub symulacji zachowania badanego obiektu w określonych warunkach

9.Metoda pojemności informacji - wyraża się macierzą

Na podstawie tych obserwacji obliczamy wektor r0, który zawiera współczynnik korelacji pomiędzy zmienną y w poszczególnymi wartościami objaśniającymi

10.Estymacja modelu ekonomicznego -Wyznaczanie ocen jego parametrów nadaniu im liczbowej postaci.

11.Warunki stosowania KMNK

a).Szacowany model jest modelem liniowym względem parametrów lub sprowadzanym względem parametrów lub sprawdzialnym do liniowego poprzez transformację:

Y=XL+(ksi)

b).Uwzględnione w modelu zmienne objaśniające Xi są wielkościami nielosowymi czyli macierz obserwacji na zmiennych objaśniających zawiera elementy ustalone w powtarzalnych próbach;

c).Między zmiennymi objaśniającymi nie występuje współliniowość

d).Liczba zmiennych objaśniających w równaniu musi być mniejsza od liczby obserwacji czyli k<n

e).Składnik osoby jest zmienną losową której wartość oczekiwana jest równa zero a wariancja jest stała nie zależna od czasu

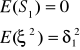
f).Obserwacje są niezależne z czego wynika że ksi_k i ksi_l są niezależne

Gdzie Y są to teoretyczne wartości zmiennej objaśnianej wynikające z modelu

Można więc zapisać: R3

Szacowanie parametrów polega na zastąpieniu parametrów L1+L2+...+Lk ich ocenami uzyskanymi na podstawie próby A0,A1,A2...Ak

12.Suma kwadratów reszt modelu (warunek najmniejszych kwadratów

13.Parametry struktury stochastycznej:

Wariancje estymatorów oraz ich pierwiastki czyli średnie błędy szacunku.

Macierz wariancji i kowariancji ocen parametrów

Standardowy błąd szacunku parametru - pierwiastek z wariancji oceny danego parametru S(a)

Informuje o ile jednostek wartość oceny parametru różni się od rzeczywistej wartości parametru

14.Macierz wariancji i kowariancji

-astymulator wariancji resztowej obliczamy wg wzoru

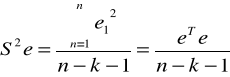
Pierwiastek z wariancji resztowej zwany jest odchyleniem standardowym reszt S informuje o ile jednostek przeciętne rzeczywiste wartości zmiennej objaśnianej różnią się od teoretycznych wartości tej (wyznaczonych modelu).

15.NIELINIOWE MODELE EKONOMICZNE

W ekonometrii wyróżniamy

-modele liniowe i nieliniowe względem parametrów

Liniowość modelu względem parametrów stwierdza się obliczając pochodne cząstkowe zmiennej zależnej względem wszystkich parametrów. Jeżeli każda z pochodnych jest niezależna od parametrów modelu to taki model jest liniowy względem parametrów.

-modele liniowe i nieliniowe względem zmiennych.

16.Charakter funkcji wykładniczej:

-zależność kosztów całkowitych produkcji Y od wielkości produkcji X

Funkcja wykładnicza znajduje najczęściej zastosowanie jako model tendencji rozwojowej w którym występuje tylko jedna zmienna objaśniająca tj. zmienna czasowa t.

Funkcja Alfa 0

Sprowadza się do postaci liniowej przez logarytmowanie

17.Model potęgowy

Model potęgowy k zmiennych objaśniających X1 wyraża się funkcją

Modele powyższej postaci znajdują szczególne zastosowanie do opisu zjawisk ekonomicznych w którym elastyczność zmiennej objaśnianej względem zmiennych objaśniających X1,X2,...,Xk jest stała.

Wzrost X1 o 1% powoduje wzrost Y o około alfa % przy założeniu stałości powstałych wszystkich zmiennych objaśniających.

Nieliniowy model potęgowy sprowadzamy do modelu liniowego przy zlogarytmowaniu obu stron równania

18.Weryfikacja modelu -Weryfikacja modelu polega na wszechstronnej różnorodnej jego ocenie

19.Koincydencja:

Model jest koincydentalny jeżeli zachodzi zgodność znaków wszystkich współczynników korelacji zmiennej objaśnianej ze zmiennymi objaśniającymi a znakami odpowiadających im parametrów strukturalnych modelu.

20.Ocena statystyczna:

-ocenie dopasowana modelu

-ocenie istotności wpływu zmiennych objaśniających na zmienną objaśnianą

-sprawdzeniu własności składnika losowego

21.Miary dopasowania modelu:

Współczynnik determinacji wyrażony w % informuje ile % zmienności zmiennej objaśnianej jest objaśnienie przez zmienność zmiennych objaśniających R^2

Rozkład reszt w dobrym modelu powinien:
1.być symetryczny- co oznacza liniowość modelu

2.losowy

3.nie powinno być skorelowania reszt (żądamy by nie występowała autokorekcja reszt)

4.wariancje składanych losowych i reszt powinny być stałe (jednorodne) - stabilność wariancji

5.normalny

22.Badamy ciąg reszt:

-reszty dodatnie - przyporządkujemy symbol A

-reszty ujemne - przypisujemy symbol B

-reszty równe zero odrzucamy

1.w ciągu uzyskaniu ciągu liter A i B obliczamy liczbę serii r

23.Seria - podciąg jednakowych liter, który poprzedzony jest i po którym następuje inna litera od liter znajdujących się w podciągu

2.Obliczamy liczbę liter A w ciągu reszt - n1 oraz liczbę liter B w ciągu reszt -n2

3. dla przyjętego poziomu istotności alfa oraz liczb n1 i n2 odczytujemy wartość krytyczną r-krytyczne z tablic serii.

Jeśli r jest mniejsze równe r krytycznego to hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej. Przemawia to za nieliniowością modelu. Jeśli r> r kryt. To nie ma podstaw do odrzucania hipotezy zerowej mówiącej o liniowości modelu to jest liniowej zależności zmiennej objaśnianej od zmiennych objaśniających.

Przedstawiona weryfikacja polega na badaniu losowości reszt. Dlatego ważny jest porządek według którego formowany jest ciąg reszt. Jeżeli weryfikowany model jest modelem:

-z jedną zmienną objaśniającą to porządkujemy reszty w kolejności odpowiadającej rosnącym wartością zmiennej objaśniającej.

-o wielu zmiennych objaśniających a dane zaobserwowane stanowią szeregi czasowe to porządkujemy reszt według numerów obserwacji,

-o wielu zmiennych objaśniających a wielkości obserwowane w próbie stanowią szeregi przekrojowe to reszty można uporządkować według rosnących wartości wybranej zmiennej objaśniającej najczęściej wybieramy zmienną posiadającą największy wpływ na zmienną objaśnianą.

24.Test Durbina - Watsona

Po wyznaczeniu parametrów modelu MNK i obliczeniu reszt określamy współczynnik p jeśli:

-obliczamy współczynnik z próby p jest dodatnie to

stawiamy hipotezę zerową H0; p=0

przy hipotezie alternatywnej H1; p>0

-obliczamy współczynnik z próby p jest ujemny to stawiamy hipotezę zerową H0: p=0

przy hipotezie alternatywnej H1: p<0

Statystyka Dubrina -watsona

wartość statystyki d zawiera się w przedziale <0,4>

Test Durbina - Watsona można stosować do modelu z wyrazem wolnym w którym nie występuje opóźniona zmienna objaśniana jako zmienna objaśniająca i o składniku losowym posiadającym rozkład normalny.

Rozkład statystyki d jest stablicowany i zależy od liczby obserwacji n (n>14) i liczby zmiennych objaśniających k .

Dla ustalonego poziomu istotności alfa i parametr n i k odczytujemy dwie wartości krytyczne: wartość dolną dl i wartość górną du

25.Test Hellwiga - badanie normalnośći rozkładu składnika

1.przeprowadzamy standaryzację reszt modelu:

Gdzie e - średnia arytmetyczna reszt et, t=1,2,...,n; se - odchylenie standardowe reszt (dla modeli liniowych szacowanych MNK e=0)

2.standaryzowanie reszty porządkujemy według wartości niemalejących (tworząc ciąg niemalejący).

U(1) mniejsze równe u(2) <...<u(n)

3.Z tablic dystrybuanty rozkładu normalnego N(0,1), odczytujemy wartość dystrybuanty F (U(1)) dla uporządkowanych standaryzowanych reszt

4.Wyznaczamy podprzedziały liczbowe lt(t=1,2,...,n) o długości 1/n powstałe z podzielenia przedziału <0,1> na n równych części.

5.Wartość dystrybuant F(U(1)) przyporządkowujemy do poszczególnych podprzedziałów a następnie liczymy liczbę podprzedziałów K, to jest takich do których nie trafia żadna wartość F(U(t))

6.Z tablic testu zgodności Hellwiga dla danej liczby obserwacji n i przyjętego poziomu istotności alfa odczytujemy krytyczną liczbę pustych podprzedziałów K*

7.Jeżeli K<K* to nie ma podstaw do odrzucenia hipotezy o normalnym rozkładzie reszt. Jeżeli K>=K* to hipotezę zerową należy odrzucić na rzecz hipotezy alternatywnej według której rozkład reszt nie jest normalny.

1

---