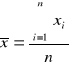
Laboratorium z Metrologii	Data wykonania ćwiczenia: 2010.03.10
Temat: Badania porównawcze własności metrologicznych przyrządów.	Grupa 203
Ćwiczenie wykonywali:	Ocena:

• Wstęp teoretyczny

W praktyce pomiarowej dość często występuje konieczność pomiaru w różnych warunkach i w odmiennym przedziale czasu tych samych parametrów badanych obiektów.

Przykładowo wykonano dwie serie pomiarów tego samego parametru produkowanego obiektu w różnych odstępach czasu. Otrzymane wartości różnią się znacznie od siebie. Powstaje wątpliwość czy fakt ten spowodowany jest wpływem czynników zewnętrznych, które przyczyniły się do powstania znacznych błędów systematycznych, przez co różnice otrzymanych wartości parametru można uznać za nieprzypadkowe , czy też wpływ na ten stan rzeczy mają mieć czynniki przypadkowe i w związku z tym różnice wartości mierzonych parametrów tych samych wielkości są nieistotne.

Również w wielu przypadkach występuje sytuacja , w której ten sam parametr mierzony jest dwoma tego samego typu przyrządami pomiarowymi w identycznych warunkach, w jednakowym czasie. W wyniku przeprowadzonych pomiarów uzyskuje się różne wartości mierzonego parametru , co może być związane z różną wiernością wykorzystanych przyrządów pomiarowych.

Powyższe zagadnienia mogą być rozstrzygnięte przy wykorzystaniu statystyki matematycznej w oparciu o badania statystyczne związane z weryfikacją hipotez statystycznych. Niekiedy tego typu badania statystyczne zwane są testami statystycznymi. Dwa takie testy przeprowadzono poniżej.

• Porównanie wartości średnich w dwóch populacjach:

Lp.	d [mm]	Lp.	d [mm]	Lp.	d [mm]
1	15,49	11	15,54	21	15,57
2	15,50	12	15,55	22	15,54
3	15,53	13	15,58	23	15,58
4	15,56	14	15,53	24	15,58
5	15,52	15	15,55	25	15,59
6	15,53	16	15,53	26	15,53
7	15,51	17	15,52	27	15,54
8	15,49	18	15,58	28	15,58
9	15,54	19	15,59	29	15,59
10	15,55	20	15,53	30	15,57

Lp.	d [mm]	Lp.	d [mm]	Lp.	d [mm]
1	13,02	11	13,03	21	13,02
2	13,04	12	13,08	22	13,07
3	13,05	13	13,04	23	13,06
4	13,08	14	13,06	24	13,04
5	13,05	15	13,07	25	13,09
6	13,04	16	13,01	26	13,05
7	13,07	17	13,09	27	13,04
8	13,08	18	13,05	28	13,02
9	13,09	19	13,04	29	13,06
10	13,03	20	13,06	30	13,05

a) obliczenie wartości średnich x₁ i x₂:

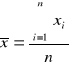
x_i -wynik pomiaru

n - liczność populacji

x'₁= 15,55

x'₂= 13,05

b) obliczenie wartości wariancji s₁² i s₂²:

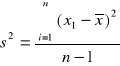
x_i -wynik pomiaru

n - liczność populacji

s₁² = 0,009

s₂² = 0,0005

c) wyliczenie wartości statystyki:

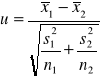
u = 140,4878751

d) odczytanie z tablic wartości krytycznej u_α dla poziomu odniesienia α = 0,05

u_α = 1,645

e) wobec otrzymanych wyników oraz z porównania wartości u z wartością u_α odrzucamy hipotezę zerową H₀: m₁ = m₂ na korzyśc H₃: m₁ > m₂

• Porównanie wariancji w dwóch populacjach:

Mikrometr 1

Lp.	d [mm]	Lp.	d [mm]	Lp.	d [mm]
1	15,85	11	15,86	21	15,85
2	15,86	12	15,88	22	15,89
3	15,89	13	15,94	23	15,83
4	15,95	14	15,88	24	15,88
5	15,89	15	15,84	25	15,85
6	15,90	16	15,87	26	15,90
7	15,87	17	15,93	27	15,89
8	15,88	18	15,86	28	15,86
9	15,86	19	15,84	29	15,85
10	15,84	20	15,86	30	15,84

Mikrometr 2

Lp.	d [mm]	Lp.	d [mm]	Lp.	d [mm]
1	15,53	11	15,54	21	15,62
2	15,55	12	15,56	22	15,60
3	15,54	13	15,61	23	15,59
4	15,56	14	15,60	24	15,61
5	15,57	15	15,58	25	15,56
6	15,58	16	15,60	26	15,63
7	15,53	17	15,59	27	15,57
8	15,56	18	15,59	28	15,61
9	15,56	19	15,57	29	15,56
10	15,54	20	15,59	30	15,57

a) obliczenie wartości wariancji s₁² i s₂²:

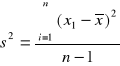
x_i -wynik pomiaru

n - liczność populacji

s₁² = 0,0009

s₂² =0,000755

b) ponumerowanie serii aby s₁² > s₂² oraz obliczenie statystyki F:

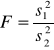
F = 1,191781

c) oszacowanie stopni swobody i odczytanie wartości krytycznej statystyki dla n₁-1 i n₂ -2 dla poziomu odniesienia α = 0,05:

F_α=1,84

d) ponieważ F_α > F należy przyjąc, że s₁² = s₂².

• Wnioski

W wyniku przeprowadzonego doświadczenia oraz testu statystycznego można wysnuć następujące wnioski:

• w przypadku czujnika pomiarowego uzyskuje się wierniejsze wartości niż w przypadku mikrometru,

• z przeprowadzonych testów wynika, że wartości mierzone czujnikiem będą przyjmować zbliżone wartości w różnych warunkach.

Stosowane przyrządy pomiarowe mają znaczący wpływ na jakość otrzymywanych wyników. Każdy pomiar przyrządem niesie ze sobą pewien błąd systematyczny. Zależy on nie tylko od jakości wykonania danego przyrządu ale także od jego rodzaju. Poprawne wykonanie pomiaru wymaga bezwzględnej znajomości instrukcji obsługi jak i zakresów pomiarowych przyrządu. Przyrządy pomiarowe z biegiem czasu tracą swe początkowe własności. Dlatego też należy co pewien okres dokonywać kalibracji. Kalibracji najwygodniej dokonać przez porównanie z przyrządem o wyższej klasie dokładności.

W wielu przypadkach dochodzi często do potrzeby porównania dwóch wartości średnich tego samego parametru otrzymanych w wyniku przeprowadzonego eksperymentu w innych warunkach i odmiennym czasie. Pojawienie się w procesie technologicznym bądź w czasie pomiaru błędów systematycznych powoduje, że każdy wynik pomiaru w przeprowadzonej serii będzie obarczony stałym błędem. W sytuacji kiedy rozbieżność średnich jest istotna można domniemywać, że wyniki pomiaru z jednej serii są obarczone błędem systematycznym. Badania statystyczne z zakresu porównywania wartości średnich mają również duże znaczenie przy porównywaniu poprawności narzędzi pomiarowych. Zgodnie z przyjętą zasadą wyznaczanie błędu poprawności polega na porównaniu otrzymanej średniej wartości pomiaru z wartością poprawną mierzonej wielkości.

---